空间机动目标跟踪的改进自适应IMM算法

尹聚祺, 杨 震, 罗亚中, 周剑勇

(国防科技大学空天科学学院, 湖南 长沙 410073)

0 引 言

随着航天技术的发展,在轨空间目标数量急剧增长,使得太空环境越来越拥挤[1-3]。未来,具有自主机动能力的空间非合作目标对己方航天器的自主异常接近将对己方航天器安全产生重大威胁,天基在轨自主空间态势感知能力对己方航天器在轨安全防御显得至关重要[4-6]。通过轨道机动,空间目标可按需要逼近其他目标。一般而言,空间目标的机动方式可建模为两种[7]:① 脉冲机动;② 有限推力机动。本研究重点关注前者,即空间非合作目标在脉冲机动控制下的状态估计问题。

近年来,空间非合作机动目标跟踪问题受到广泛关注,常用研究方法包括单模型方法和多模型方法。由于非合作性,目标机动发生时刻和脉冲推力大小均为未知量,传统单模型滤波方法往往在机动发生时由于模型失配造成滤波发散或精度降低。Fitzgerald[8]分析了当被跟踪目标具有机动属性时,由于标称动力学与实际机动不匹配,传统卡尔曼及扩展卡尔曼滤波(extended Kalman filter,EKF)算法的跟踪性能下降甚至发散。Zhou等[9]基于残差序列正交化的思想提出强跟踪滤波(residual-normalized strong tracking filter,RNSTF)算法,提高了单模型滤波算法对机动信息的鲁棒适应能力,但对脉冲机动敏感性不足而易导致滤波精度下降。Jiang等[10]针对这一问题进一步提出残差归一化的RNSTF方法,能更及时地检测机动并提高机动后的跟踪精度,但整体跟踪精度仍有待提到。由于单模型方法不能有效适应目标运动过程中的各种运动状态,在非合作机动目标跟踪问题上应用受限,因此发展出了多模型方法。

最著名的多模型方法是Blom等[11]提出的交互多模型(interacting multiple model,IMM)算法。IMM算法通过选择恰当的模型集来匹配目标运动过程中的状态变化,通过模型转移概率将各模型输出结果进行交互,在机动目标跟踪方面具有适应能力强的优势,被广泛应用到机动目标跟踪问题中[12-18]。在空间机动目标跟踪领域,Lee等[19]基于IMM算法给出一种空间目标机动检测和机动后轨道表征算法。Goff等基于IMM算法和协方差膨胀思想来解决脉冲机动目标状态跟踪问题,提出一种非合作机动目标实时跟踪算法[20],但存在漏检情况。针对连续推力机动目标跟踪问题,Goff等将IMM算法与可变状态维度滤波器相结合,提出一种自适应变维滤波估计算法[21]。Xiong等[22]将鲁棒卡尔曼滤波与IMM算法相结合,提出一种鲁棒多模自适应算法。Huang等[23]基于IMM估计算法,结合Singer模型及无迹卡尔曼滤波方法,给出了超音速滑翔目标跟踪方法。以上文献进行了富有价值的研究,但基于传统IMM算法设计的估计方法为提高算法适应能力存在模型集设计复杂,且估计精度不高的问题。

在传统IMM方法中,模型转移概率参数一般设计为先验给定的固定值。由于目标运动的不确定性,该固定先验假设的模型概率转换方式是模型切换与未切换情况下的折衷[24]。模型转移概率的先验不确定性会造成滤波精度的损失,因此对其进行改进的在线自适应性估计方法一直是国内外的研究热点。Lee等[25]通过将未知机动信息建模为特定条件下状态变化问题,从而使得模型转移概率自适应变化,然而这仍需要一定的先验信息。国内学者针对该问题进行了详细研究[26-30]。郭志[29]和许登荣[30]分别从模型概率和模型似然函数的角度出发,分别将平方根容积卡尔曼滤波器(square-root cubature Kalman filter,SRCKF)、强跟踪修正输入估计(strong tracking modified input estimation,STMIE)及匀速运动(constant velocity,CV)模型引入IMM算法中,提出了IMM-SRCKF及IMM-STMIECV算法对模型转移概率进行自适应性改造,改善了模型切换速度和滤波精度。模型似然函数值从量的角度衡量了该模型的匹配情况,但简单基于模型似然函数比来对模型转移概率进行自适应修改在目标机动时刻存在奇异问题。

本文基于IMM算法,并结合文献[30]模型转移概率自适应算法,研究了追踪星(空间非合作目标)采用脉冲机动方式接近目标星(己方航天器),目标星采用测角加测距的量测方式跟踪追踪星,在双方信息不透明情况下追踪星的相对状态估计问题。本文的创新点在于提出了一种改进自适应IMM-EKF估计方法,具体为:① 将白噪声模型与EKF算法相结合,设计了精简的模型集以适应目标机动和非机动时的状态变化;② 航天器相对运动采用直接离散化处理的非线性相对轨道动力学方程,相比于近距离、圆参考轨道及线性化假设下的Clohessy-Wiltshire(CW)方程提高了预报精度且增加了适用范围;③ 提出了一种变换函数进而克服了简单使用模型似然函数比对模型转移概率修正时存在奇异的问题。最后对比分析了加入速率测量信息对滤波结果的改善作用。仿真结果表明，本文提出的改进自适应IMM-EKF方法相比传统IMM滤波方法、IMM-SRCKF、RNSTF滤波及容积卡尔曼滤波(cubature Kalman filter, CKF)方法跟踪效果更好,引入速率量测信息后,IMM-EKF方法最大峰值误差及估计精度得到了改善。

1 相对状态预测模型

考虑离散时间非线性动力学及观测方程:

(1)

式中:X(k)∈Rn为n维为状态向量;y(k)∈Rp为p维观测向量;f(X(k)):Rn→Rn为一步状态预测方程;h(X(k)):Rn→Rp为观测方程;w(k)及v(k)分别为n维、p维零均值高斯白噪声,满足E[w(k)w(k)T]=Q(k),E[v(k)v(k)T]=R(k),且B∈Rn×l,G∈Rn×m均为常矩阵;δt,k+1为Kronecker记号函数,当t=k+1时,δt,k+1=1,t≠k+1时,δt,k+1=0;U为追踪星控制输入量,δt,k+1GU表示追踪星大小及时间均未知的机动信息。

以目标星质心为原点建立VVLH(vehicle velocity, local horizontal)坐标系,其中x轴指向目标速度方向,z轴指向地心,y轴满足右手系定则。在VVLH系下建立相对运动方程来描述追踪星和目标星的相对运动关系,则脉冲机动下的相对状态预报方程可表示为

(2)

式中:

ΔT为采样时间间隔;α为采样时刻目标星轨道角加速度;ω为采样时刻目标星轨道角速度;n为目标星平均轨道角速度;e为目标星轨道偏心率;θ为采样时刻目标星真近点角;Rc为采样时刻目标星轨道半径;μ为地球引力常数。注意到,式(2)为对二体相对非线性动力学方程的直接离散化处理,相比于近距离、圆参考轨道及线性化假设下的CW方程提高了预报精度且增加了适用范围,即目标星轨道满足椭圆情况。

2 相对状态观测模型

以运行在椭圆轨道上的目标星质心为原点建立VVLH坐标系,目标星利用自身携带设备对追踪星进行测量跟踪,测量量为相对距离、俯仰角和方位角,建立天基观测模型。在VVLH系下,如图1所示。俯仰角α定义为追踪星相对目标星的视线方向与xy平面的夹角,取值范围为(-π/2,π/2);方位角β定义为视线方向在xy平面上的投影与x轴方向的夹角,以x轴为起点逆时针转动为正,取值范围为(-π,π)，观测方程为

(3)

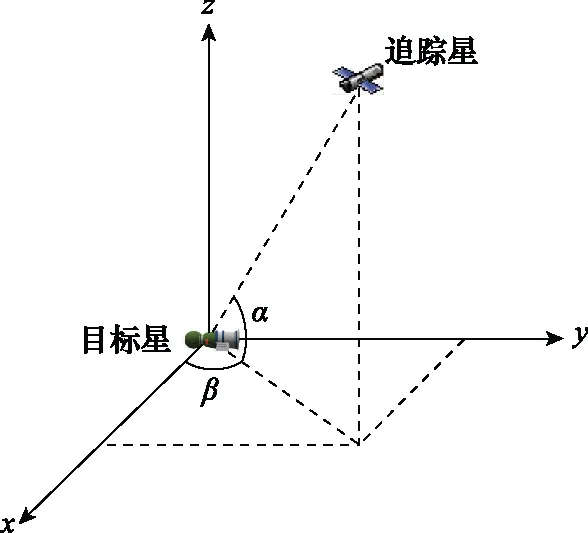
图1 观测坐标系Fig.1 Observation coordinate system

对应观测敏感性矩阵为

(4)

H各分量为

引入相对速率量测信息后,相应的观测方程及观测敏感矩阵分别为

(5)

(6)

式中:H各非0分量为

3 改进自适应IMM估计算法

当目标由非机动状态转入机动状态时,传统单模型算法一般会由于模型失配而导致滤波发散。IMM估计算法可包含多个模型以适应不同工况,通过交互融合多种模型滤波结果,在保持滤波稳定性的同时达到精度要求。

3.1 标准IMM算法

标准IMM算法包含模型输入交互、模型估计、模型概率更新和综合输出4个递推模块,下面给出从k-1时刻到k时刻的递推步骤。本研究中模型集均采用白噪声模型,滤波器为两个EKF器分别记为EKF1和EKF2。其中EKF1过程噪声Q1较小,为非机动模型;EKF2将未知的机动信息建模为较大的过程噪声Q2。

步骤 1模型输入交互

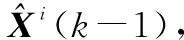
(7)

(8)

式中:mi|j(k-1)为模型i到模型j的混合概率,可由模型概率mi(k-1)和模型转移概率γij表示:

(9)

模型概率mi初值及模型转移概率γij为经验给定值。

步骤 2模型估计

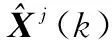
(10)

Pj(k|k-1)=F(k-1)P0j(k-1)F(k-1)T+
BQj(k-1)BT

(11)

(12)

(13)

(14)

Pj(k)=[I-K(k)H(k)]Pj(k|k-1)

(15)

K(k)=Pj(k|k-1)H(k)T·
[H(k)Pj(k|k-1)H(k)T+R(k)]-1

(16)

(17)

步骤 3模型概率更新

假设模型j的残差vj(k)服从高斯分布,其协方差为Sj(k),则模型似然函数Λj(k)和模型概率mj(k)可更新为

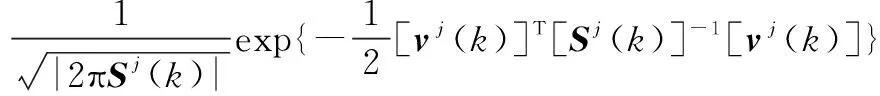
(18)

(19)

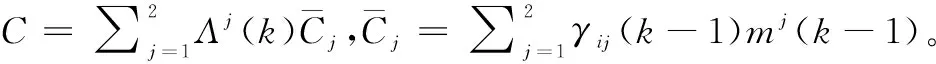
模型残差vj(k)及其协方差Sj(k)可表示为

(20)

Sj(k)=H(k)Pj(k|k-1)H(k)T+R(k)

(21)

步骤 4综合输出

(22)

(23)

3.2 模型转移概率自适应算法

(24)

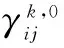
(25)

(26)

否则保持其所在行的元素不变。

3.3 改进自适应IMM算法

将第3.2节方法应用到脉冲机动目标的相对状态跟踪问题中,当采用非机动模型EKF1滤波器跟踪目标的运动时,非机动时刻具有较高精度的跟踪效果;而当目标机动时,非机动模型不能匹配目标的状态变化。这时非机动模型似然函数值接近0,采用似然函数比放大或缩小上一时刻的模型转移概率会出现奇异现象,文献[30]所提IMM模型状态转移概率自适应修正方法失效。

为解决此问题,本文在第3.2节的基础上提出非线性变换函数对模型似然函数进行变换。变换前,传统模型似然函数有以下不足:

(1)非机动模型似然函数值在机动时刻数值趋于0,导致模型似然函数比奇异;

(2)模型似然函数值在整个滤波过程中数值较大(本文算例为104～105量级),在设计可避免奇异的变换函数时,需考虑其影响。

为解决因非机动模型似然函数值在机动时刻数值趋于0而造成模型似然函数比在机动时刻奇异问题,本文采用在[0,+∞)区间上函数值不过0的自然指数函数(e)对其进行变换。然而直接采用指数函数进行变换会造成变换后的模型似然函数值无穷大的情况,进而引起数值计算错误,所以对变换函数进行如下设计。

首先，对模型似然函数进行幂函数缩放变换:

Λj1=(Λj0)η,0<η<ηmax

(27)

式中:η为缩放因子,通过选择η的大小来缩放初始模型似然函数值至一合理范围内,避免进行e指数函数变换后Λj值过大的情况。

其次，对缩放变换后的模型似然函数进行指数函数变换。

Λj=exp(Λj1)

(28)

综合式(27)和式(28),ηmax可按以下步骤确定。

步骤 1令η=0,则IMM-EKF方法退化为传统IMM方法,可确定变换前模型似然函数值量级范围Λscale。进而由计算机浮点数运算上界Valuemax确定关系方程。

exp((Λscale)η)≤Valuemax

(29)

步骤 2由式(29)求解η范围:

(30)

本文算例中Λscale取保守值106,64位计算机浮点数运算上界Valuemax约为1.797 6×10308,则可得ηmax≈0.475 2。不同η的取值将影响滤波的估计精度及机动后的收敛速度。

由于以e为底的指数函数和幂指数大于0的幂函数都是增函数,故其复合函数也是增函数,所以可以通过选择参数缩放因子η的值,在不改变似然函数变化趋势的情况下使得变换后的模型似然函数值Λj≥1,避免采用第3.2节方法对模型转移概率进行自适应修正时出现奇异现象。

图2给出了研究的模型转移概率自适应IMM算法框图。实线表示k-1时刻算法计算流程,虚线表示由k-1时刻更新至k时刻,进行下一步计算。

图2 模型转移概率自适应修正算法框图Fig.2 Diagram of adaptive correction algorithm for modeltransition probability

4 仿真算例分析

为验证改进方法的有效性,首先仿真分析了所提变换函数的有效性;其次,将与传统IMM算法、IMM-SRCKF算法、RNSTF滤波及CKF滤波方法对比分析,说明改进后的IMM算法在跟踪效果上的优势;最后,仿真对比分析引入速率测量信息对滤波延迟及最大峰值误差的改善效果。

4.1 仿真场景及参数设置

假设目标星运行在地球同步轨道上,追踪星在脉冲机动控制下接近目标星,目标星采用光学相机和激光测距仪对追踪星进行观测测量,实时获得相对距离、俯仰角和偏航角参数,估计两者间相对状态,如图3所示。

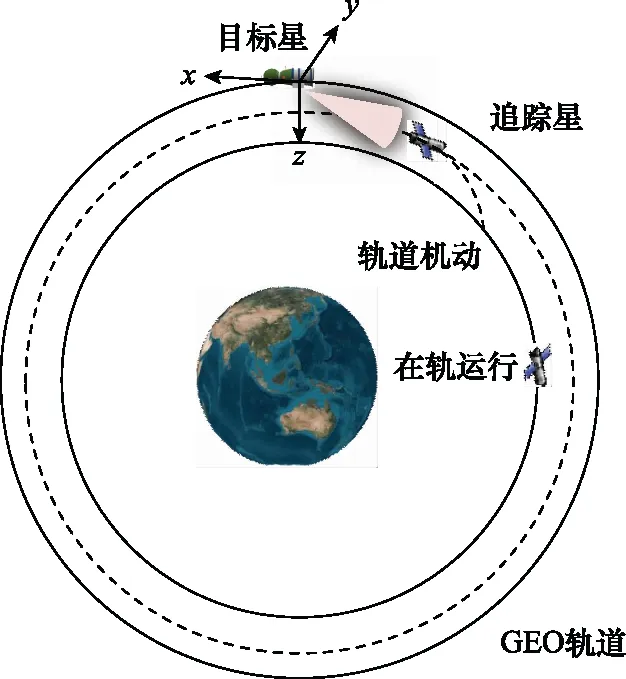
图3 仿真场景示意Fig.3 Simulation scenario

设激光测距仪测距误差标准差为1 m,光学相机角度测量误差标准差为0.001 rad,测量频率为1 Hz。目标星初始轨道根数如表1所示。在以目标星质心为原点的VVLH系下,追踪星相对目标星X(0)=[-60 000 m,5 000 m,20 000 m, 30 m/s,-5 m/s,-5 m/s]T,且在仿真过程中,假设追踪星在t=300 s和t=800 s时作两次机动,脉冲为[10 m/s,0 m/s,5 m/s]T、[0 m/s,2.8 m/s,-9.8 m/s]T。

表1 目标星初始轨道根数

多模型方法模型转移概率矩阵设为

各模型j(j=1,2) 初始模型概率、滤波估计初值、初始协方差矩阵及过程噪声协方差矩阵设置为

mj(0)=0.5

Pj(0)=diag(10, 10, 10, 1, 1, 1)

Q1(k)=diag(10-4, 10-4, 10-4, 10-8, 10-8, 10-8)

Q2(k)=diag(10-2, 10-2, 10-2, 102, 102, 102)

模型转移概率修正参数分别设置为γ=1/10,Th=0.85,η=1/10。

文献[30]所提RNSTF滤波方法仿真场景参数设置同IMM滤波方法一致,渐消因子设为ρ=0.95,CKF仿真参数同上。

4.2 仿真结果分析

对以上方法进行Monte Carlo仿真分析,结果如图4和图5所示。

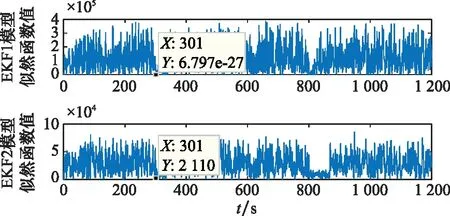
图4 变换前模型似然函数变化情况Fig.4 Change of model likelihood function before transforming

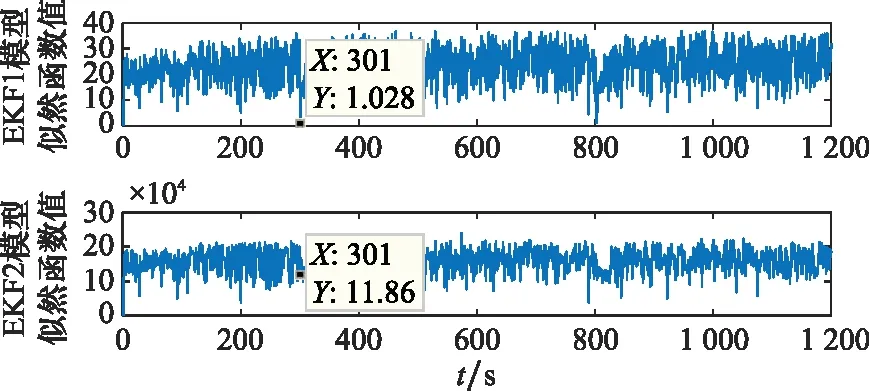
图5 变换后模型似然函数变化情况Fig.5 Change of model likelihood function after transforming

图4和图5分别给出了对IMM算法模型集中各模型似然函数进行变换前后的仿真结果。变换前,各模型似然函数值波动剧烈,波动范围在104～105量级,且模型1似然函数值在追踪星机动后趋于0,这使利用模型似然函数比对模型转移概率自适应修正时出现奇异的现象,导致滤波发散。采用本文所提方法对模型似然函数值进行变换后,各模型似然函数值波动范围大大减小,且在机动后最小值趋于1,避免了造成奇异现象,提高了算法稳定性。

表2给出了变换函数中参数缩放因子η取不同值时对所提IMM-EKF算法跟踪性能的影响统计情况,并对每类工况进行100次Monte Carlo仿真分析，统计均方根(root mean square, RMS)估计误差均值。表2中“—” 表示滤波不成功。例如,当η=1时,即变换函数为简单e指数变换,这使得变换后的模型似然函数无穷大,进而导致滤波失败。当η的值不断取小时,RMS位置及速度误差均值不断增大,但机动后的收敛速度不断加快。例如,当η值趋于0时,变换后的模型似然函数值趋于1,使得似然函数比接近1,基于似然函数比对模型转移概率矩阵不再具有修正作用,IMM-EKF滤波效果退化接近标准IMM算法。综合考虑滤波估计误差和机动后的收敛速度,本文将η的值取为0.1。

表2 不同η取值对算法跟踪性能影响的统计情况

图6给出了未考虑速率测量的多模型滤波RMS误差仿真结果。由图6分析可得,随着仿真时间推进,即两航天器间的相对距离减小,滤波估计结果的RMS位置误差呈减小趋势。相比于多模型方法,单模型RNSTF方法在全滤波时段位置和速度估计精度较低,且在追踪星机动后产生较大的峰值误差,但具有较快的收敛速度。CKF算法在全滤波阶段位置及速度估计精度较低,且对机动信息不敏感。IMM-SRCKF算法在本算例工况下无论是滤波精度还是机动发生后的收敛速度都较标准IMM算法所得结果相差不大。较于IMM、IMM-SRCKF、IMM-EKF,本文改进的模型转移概率自适应IMM-EKF算法在估计精度上具有更好效果。

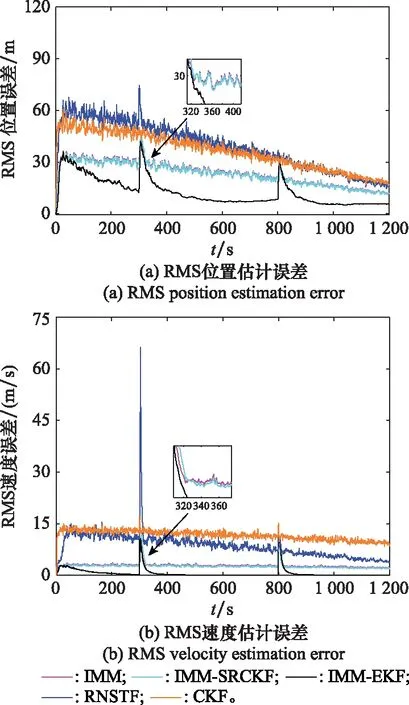
图6 未考虑速率测量的RMS误差对比分析Fig.6 Comparative analysis of RMS error without considering rate measurement

表3给出了比较的4种方法在全观测时段内RMS位置及速度平均误差,最大峰值误差及滤波结束时刻估计误差统计数据,从量化的角度说明了以上分析结论。就对比的3类指标而言,单模型RNSTF方法及CKF算法估计均具有较大的估计误差,IMM-EKF方法估计误差最小,表明了提出的IMM-EKF方法良好的估计效果。

表3 未考虑速率测量的算法跟踪性能比较

图7给出了IMM-EKF方法模型概率值变化情况。当追踪星未机动时,非机动模型EKF1占据主要地位,对应模型概率接近数值1,非机动模型EKF2模型概率接近数值0;当追踪星机动时,模型集中非机动模型EKF1预测值和测量值产生较大偏差,模型似然函数值减小,对应模型概率发生突变减小,模型概率接近数值0,机动模型EKF2模型概率接近数值1,模型切换。因此,IMM-EKF方法中模型概率值在机动发生后突变这一规律可用于目标机动检测的判断依据,实现跟踪过程中实时的机动检测,这对天基态势感知十分必要。

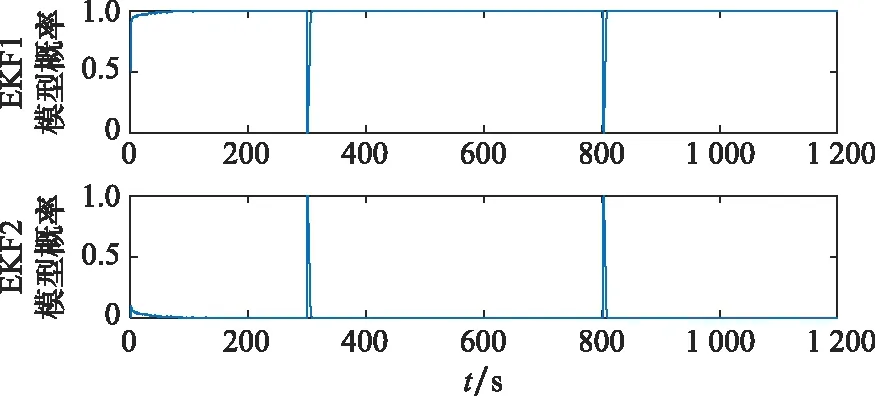
图7 IMM-EKF方法模型概率变化情况Fig.7 Change of model probability of IMM-EKF

图8给出了考虑速率测量的多模型滤波仿真结果。引入速率测量信息,滤波开始后的RMS位置及速度估计误差明显减小,且改善了最大峰值误差,机动后的收敛速度也有改善。当目标速度发生变化时,由于距离及角度测量量非瞬态响应量,目标的机动信息不能在机动时刻体现,故存在检测延迟,进而导致较大的峰值误差。对于多模型滤波,加入速率量测数据后,机动时刻,滤波器残差敏感到速率的明显变化后,EKF1模型概率由1变为0,此刻EKF2的滤波结果主导综合输出结果,由于模型不匹配造成的RMS速度误差的峰值误差较大的现象得到抑制,这种变化在发生较大机动量时更能体现。表4定量给出了速率测量信息对所提IMM-EKF方法跟踪性能的影响情况。引入速率测量信息后,IMM-EKF方法RMS位置及速度估计平均误差分别减少27.67%、60.07%,最大峰值误差分别减少7.27%、11.71%,跟踪能力明显提升。

图8 考虑速率测量的多模型RMS误差对比分析Fig.8 Comparative analysis of multi-model RMS error considering rate measurement

表4 速率测量对IMM-EKF方法跟踪性能的影响

5 结 论

空间博弈对抗条件下,对机动目标实时精准的相对状态估计是制定博弈策略的重要先决条件。本文在空间近距离追逃博弈背景下,基于IMM方法研究了目标星对脉冲机动控制下的追踪星进行相对状态估计的问题,提出了模型转移概率改进自适应IMM算法,克服了模型似然函数比在机动时刻奇异的问题。仿真结果表明:① 改进的模型转移概率自适应IMM算法相比于传统IMM、IMM-SRCKF、单模型RNSTF及CKF滤波方法,在位置和速度估计精度上明显提高;② 当追踪星机动时,模型集中非机动模型预测值和测量值产生较大偏差,模型似然函数值减小,对应模型概率发生突变减小,这一规律可作为目标机动检测依据,可在空间目标态势感知任务中用于实时机动检测与告警;③ 在本文提出的模型转移概率自适应IMM算法框架下,进一步引入速率量测信息,有效抑制滤波延迟问题,减小了多模型滤波估计方法的最大峰值误差,同时提高了跟踪精度,可见增加速率测量器件对提高机动目标跟踪精度具有重要意义。