舰载机出动离场调度优化算法
2021-11-29万兵,韩维,梁勇,郭放
万 兵, 韩 维, 梁 勇, 郭 放
(海军航空大学, 山东 烟台 264001)
0 引 言
航母是作为海上移动平台遂行立体作战任务的“巨无霸”,其制空、制海优势的发挥对舰载机空中力量的出动能力提出了高指标要求。这里的出动包含舰载机起降作业及空中任务等全作业周期,而从编队攻防角度看,航母在舰载机放飞与回收时需调转航向以提供飞机起降航向上所需的甲板风[1],此时段航母机动性及防御能力弱对起降时效性要求严苛,因此提高舰载机出动离场能力既可快速弥合此时防御盲点又同时增加飞机出动架次率进而增强空中作战能力。而出动离场作业属于任务规划与资源调度优化问题,且受到时间、空间、尾流间隔以及设备等复杂约束限制,如何快速生成不同任务驱动下离场调度优化方案意义较大。
舰载机作业调度包括任务规划、布列与调运(路径规划与跟踪控制)、机-勤务保障(资源受限项目调度)、军械转运(供应链管理)、出动离场(车间调度问题)、回收排序(单机无缓存区调度问题)等阶段优化技术研究[2]。目前,单独离场调度研究不多,但舰载机作业领域国内外学者已开展大量工作。Ryan等[3-4]在无人机上舰背景下基于多智能体仿真技术开展舰载机甲板作业全周期仿真研究,采用混合整数规划(mixed integer programming,MIP)模型抽象调度问题,并引入人-机交互将人工调度与MIP规划算法进行融合完成舰载机作业调度与规划,但对出动离场等单个环节的优化颗粒度较粗。司维超等[5]基于粒子群优化(particle swarm optimization,PSO)、遗传算法(genetic algorithm,GA)等群体智能算法对甲板布列调度、出库调度进行研究,基于多种群协作混沌智能算法进行出动调度研究。Liu等[6]开展路径规划与跟踪控制研究。苏析超等[7-8]基于人机匹配机务勤务保障及基于Memetic一体化保障调度,采用了遗传算法的双种群和局部邻域改进策略进行优化搜索。Wu等[9]基于任务分配与排序算法开展起降任务规划方法研究。张智等[10]基于遗传算法的舰载机甲板避碰规划研究。上述学者对舰载机作业调度的研究多采用元启发式智能搜索算法及改进算法,尽管算法有效,但群智能算法属于黑箱变邻域搜索技术,对连续优化问题效果显著,而对混合整数规划离散优化问题,特别在其约束复杂情况下,此类算法缺点也较为突出,存在种群迭代过早收敛、优化参数过于敏感导致适应性不强问题[11]。因此,针对传统群体智能算法所存在不足,本文考虑采用约束规划技术进行优化研究。
约束规划是源于人工智能社区的技术,近年来,与运筹学优化技术综合运用来求解部分大规模离散优化问题[12]。约束规划是在实际优化问题完成约束规划建模后,将最小化目标函数进行约束化处理后,嵌入到约束满足问题当中,尔后通过迭代求解该约束满足问题,最终收敛到gap阈值内的优化迭代过程。目标约束化处理的初始值,需要启发法来构建,初始值的好坏将直接影响约束满足问题的搜索求解效率,实际处理时初值主要由理论值来估算。该技术本质上类似于分枝定界精确解法的树搜索技术,是对约束规划模型的解空间的搜索,但有两个重要的不同点:① 约束规划模型基于数学约束、逻辑约束、集合约束等可直观理解的复杂约束,有别于传统的数学规划模型;② 算法求解是目标约束化后的约束满足问题的迭代优化过程,约束传播和领域缩减伴随整个迭代过程和约束满足的一致性检查[13-14],最终使得约束规划模型的解空间更紧,极大地裁剪掉无效搜索分枝。目前,针对大规模离散优化问题特别是约束复杂条件下,约束规划技术优势明显,业内已有不少成熟的约束规划优化器,比如IBM ILOG Cplex(商业)、Google Ortools(开源)的优化工具,比同型问题用数学规划的求解效率提升非常多。国内于2018年也推出了混合整数规划优化器,但针对是的数学规划模型而非约束规划问题。
本文在数学规划模型基础上开展约束规划建模,借鉴现有约束规划技术成果,提出约束规划二分法迭代算法+单机约束引导启发式搜索算法来求解出动离场调度优化问题,最后进行实例仿真与算法分析,比较本算法与传统启发式算法性能,探求本算法的在线规划调度能力,分析研究起飞位使用情况与出动效能的关系。
1 舰载机出动离场作业描述
舰载机起降作业过程包括出动与回收,从上次飞行活动结束或一个新的飞行周期开始。通常包括以下过程:① 出动任务规划;② 战斗布列与保障;③ 滑行调运;④ 起飞位选择与出动离场;⑤ 回收排序与进近着舰;⑥ 回收系停。而出动作离场作业为本文研究内容,是舰载机起降作业的关键一环,其出动效能高低将直接影响航母整体作战能力[15-17]。这里,出动效能主要由出动离场作业调度优化来体现,因此求解该调度优化问题是核心。出动离场作业流程为:在已知布列并完成机务勤务保障情况下,先后进行起飞位分配、停机位滑行到起飞位准备位、排序等待、起飞前检查、弹射出动离场,单机出动离场过程如图1所示。而舰载机出动通常是完成多机编队的起飞调度,单机符合图1流程,但是对机队出动而言,调度问题可由图2所示的网络图来表述,属于一个经典的柔性作业车间调度问题(flexible jop-shop scheduling problem,FJSP)。当然由于甲板作业的复杂特性,出动调度优化还应考虑空间约束、避碰、飞机尾流间隔等约束。

图1 单机出动离场工序及作业环节Fig.1 Sortie departure process and operation link of single aircraft
图2中FJSP描述:工序1,停机位出动准备(开始-虚工序);工序2,起飞位分配及滑行入位;工序3,偏流板冷却(等待);工序4,起飞前检查;工序5,起飞出动;工序6,飞机离场(结束-虚工序)。其中,工序1为虚工序,待出动飞机所处的停机位数量即为机器数,共有pn1台机器;工序2~4为串行工序,均有ptn2个机器;工序5虽有rtn2条起飞跑道,但考虑到起飞安全1次仅能起飞1架飞机,即为1台机器;工序6同样为虚工序,共1台机器。例如,对于有3个起飞位弹射出动的某航母,离场调度问题则是解决n架飞机完成起飞位分配、出动排序、按序保障、离场。为研究方便,将起飞飞机间的安全尾流间隔纳入到离场这个工序当中。

图2 出动离场作业网络图Fig.2 Network diagram of sortie departure operation
2 出动离场模型
出动离场调度问题影响因素较多,为简化抽象成FJSP模型方便相关研究,作如下合理假设:① 出动过程稳定不中断;② 出动飞机已完成保障并系泊于相应初始停机位;③ 甲板滑行选择路径库中最优路径,忽略甲板滑行中避碰防止的等待时间(由于滑行避碰相让时间极短,可以通过调整滑行速度来调节),时间相对较为固定;④ 起飞位的弹射准备的作业时间由飞机类型决定,同型飞机准备时间相同。
2.1 参数定义
i:飞机编号,i∈N={1,2,…,n};
j:飞机工序号,j∈Ti,Ti为飞机i工序集;
k:工序j加工机器号,k∈Mj,Mj为工序j的加工机器集,且有∪Mj=M;


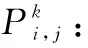
TRp,2(t):飞机p在工序2(滑行段)的实时路线,避碰检查;
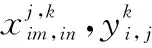
(1)
式中:(im,in)∈Ejk表示第j工序时在机器k上的连续两架作业飞机。
(2)
作业开始、完成时间与0~1变量关系如下:
(3)
(4)
式中:Sti, j、Cti, j分别为飞机i第j工序的具体作业开始时间、结束时间;NaN为非数。
2.2 混合整数规划模型
(5)
s.t.
(6)
(7)
(8)
(9)
(10)
(11)
(12)
j=6,∀k∈M6,(ip,iq)∈E6k
(13)
(14)
在MIP中,目标函数为离场作业时长最大值的最小化。式(6)表示为任意飞机和工序同时只能在一台机器作业;式(7)表示任意工序上每台机器,每次只能至多加工1架飞机;式(8)为飞机在机器上加工时间约束;式(9)为同一飞机前后工序开始与完工时间要求;式(10)为同一机器前后飞机加工优先约束,式中H为大正数确保约束始终成立;式(11)为起飞离场过程机器选择约束,起飞位确定后相应操作工序机器也随之被确定;式(12)表示离场升空工序的安全约束要求,同时只能放飞1架飞机;式(13)表示工序6中前后两架起飞飞机的安全离舰间隔(尾流安全),其中ΛT表示相邻起飞飞机的最小间隔时间;式(14)为甲板滑行段飞机在空间防碰撞安全约束要求,工序2中任意时刻两机位置满足飞机p的轨迹TRp,2(t)和飞机q之间的距离TRq,2(t)大于等于最小间隔距离Dsafe。
2.3 约束规划模型
目前多数学者主要思路,是基于数学规划创建舰载机出动离场调度的混合整数规划模型,采用精确解法或智能算法等求解。实际出动离场的约束问题远比传统数学约束要复杂,除常规数学约束外,还有析取约束、合取约束、逻辑约束、一元约束等。当然数学规划与约束规划两者是等价的,只是从模型建立与约束表达来讲,约束规划建模更为简洁、精炼且更体现实际问题逻辑表达。约束规划模型在上述整数规划模型基础上进行调整建立。
2.3.1 决策变量
(1) 间隔变量1(飞机作业)
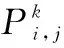
(2) 间隔变量2(机器作业)
(3) 序列变量
Sequenc mchs(k,t,o): mps(k,t,o)|k,表示对第k台机器,其序列变量mchs(k,t,o)是对间隔变量mps(k,t,o)的一个排序。其他符号见第2.1节。
2.3.2 目标函数
(15)
式中:endOf(ops(i,j,o))为间隔变量完工时间。
2.3.3 约束条件
(1) 同一架飞机作业工序的前后时序约束
当元组o1=
endBeforeStart(ops[o1],ops[o2])
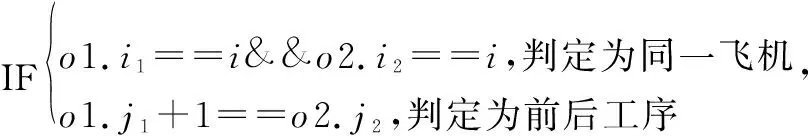
(16)
(2) 可选机器约束
出动作业时,飞机某一工序可由不同机器完成,飞机作业的间隔变量可从可选机器作业变量中任选其一进行调度设计。元组O=
alternative(ops[O]|IFm.o==O.o)←mps[m],
∀O∈{Ops},∀m∈{Mps}
(17)
式中:条件m.o==O.o,表示飞机作业数据中与机器作业数据中任务数相同情况;alternative为从mps[m]可选集中选定值赋予ops[O]。
(3) 关联机器约束
出动时,飞机i滑行、等待位、起飞前检查、出动等工序在滑行工序确定起飞位(某机器)后,该飞机后续工序机器要求也确定,约束表示为
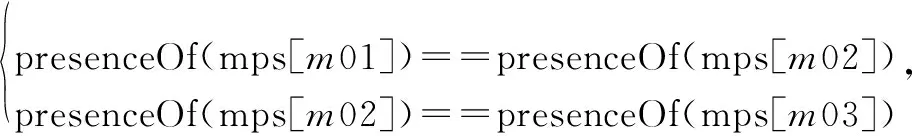
∀i∈N,∀c∈{Continuities},∀m01,m02,m03∈{Mps}
(18)
式中:元组c=

图3 出动各工序间机器关联关系图Fig.3 Association diagram of machines among each processduring sortieing
(4) 交叠约束
同一机器作业任务前后时序无交叠,约束表示为
noOverlap(mchs[k]),∀k∈M
(19)
式中:mchs[k]为第k台机器作业的排序,是对该机器作业间隔变量mps(k′,t′,o′)|IFk′==k的编排,最后要确保各间隔相互无交叠。
(5) 甲板滑行防碰撞约束
调度设计过程中,飞机滑行、等待、出动等过程中安全间隔的检查,满足最小间隔距离Dsafe,同式(14)。
综合式(15)~式(19),便是对第2.2节中数学规划模型的调整为约束规划模型。建模过程更加注重对实际调度问题的描述,贴合人们思维习惯。
3 求解算法的给出
本文将出动离场调度问题抽象为一个FJSP模型,但同时应考虑滑行阶段各飞机的路径设计与碰撞防止问题。因此,出动离场这个FJSP问题涉及到不同生产线的空间干涉约束,使得求解变得更加困难。而现实调度中既要考虑解的最优性又要兼顾求解的时效性,必须设计出快速有效的算法。对于FJSP问题,多采用群体智能算法,如PSO算法、双种群GA(double population GA, DPGA)、差分进化(differential evolution, DE)算法、蜂群算法等,也有基于MIP的分枝定界等精确求解算法,本文采用约束规划算法进行求解。
为方便问题研究,该约束规划模型简写为
minimizez=g(ops(i,j.o))
(20)
(21)
决策变量:间隔变量ops,mps及各机器作业序列变量mchs。
3.1 约束引导启发式算法(算法1)
混合车间调度问题通过阶段任务分配、单机调度设计两个阶段迭代优化完成,任务分配结合第3.2节算法作以说明,单机调度设计则由约束引导启发式搜索算法完成。单机调度是调度领域中经典、基础的作业方式。单机调度利用约束满足算法[13],求解最大完工时间(makespanCmax)使得满足小于或等于给定截止时间要求。该算法要求每台机器对其分配任务进行操作排列,使得调度方案满足时间窗约束及模型其他约束。
3.1.1 进行初始化操作
对每个作业进行编排以确定其在每台机器上的最早可能开始时间和最晚可能完成时间。在所有的时间窗已经编排好后,在每台机器上所有操作的时间窗互相之间进行比较。当任意给定机器的两个作业时间窗没有交叠时(满足一台机器同时只能进行一种作业任务的约束),这两个作业时间窗的先后关系可以增加到约束规模型中,即:在任何可行调度方案中,具有更早时间窗的作业任务必须早于这个后续时间窗的作业。实际上,优先关系在时间窗有交叠时也可以推理出来。在当前先后优化约束集合中,由S′ki(S″ki)表示作业(k,i)最早(最晚)可能的开始时间,C′ki(C″ki)表示作业(k,i)最早(最晚)可能的完成时间。这里,作业(k,i)最早可能开始时间S′ki视为该作业在实际开始时间,记为rki;而作业最晚可能完成时间C″ki视为该作业在实际交货时间,记为dki。那么,在机器k上作业(k,i)与(k,j)之间的作业间隔松弛间隙可以表示为
(22)
式中:作业(k,i), (k,j)表示机器k上加工任务i,j,k∈{Machines},i,j∈{Operations};rki表示作业(k,i)的现场开始时间;dki表示作业(k,j)的现场的交货时间。
图4详细说明了以上几个表达式时间含义,其中作业(k,i) 先于(k,j),图中情况i)任务作业时间窗则表示前两式,情况ii)则表示最后一式。如果δ(k, i)→(k, j)<0,那么在图4中的任务优先约束情况下不存在可行的调度方案,说明此时作业(k,j)先于(k,i)。在程序初始化阶段,所有作业时间窗(也称为间隔变量)两两之间相互比较,所有隐含的作业优先级关系将插入到析取图中。因为这些新增的优先级约束,每个作业的时间窗将会再次调整,或者说更加紧凑(即δ(k, i)→(k, j)将进一步压缩),这里将包含对每个任务作业的开始与交货时间进行重新编排。
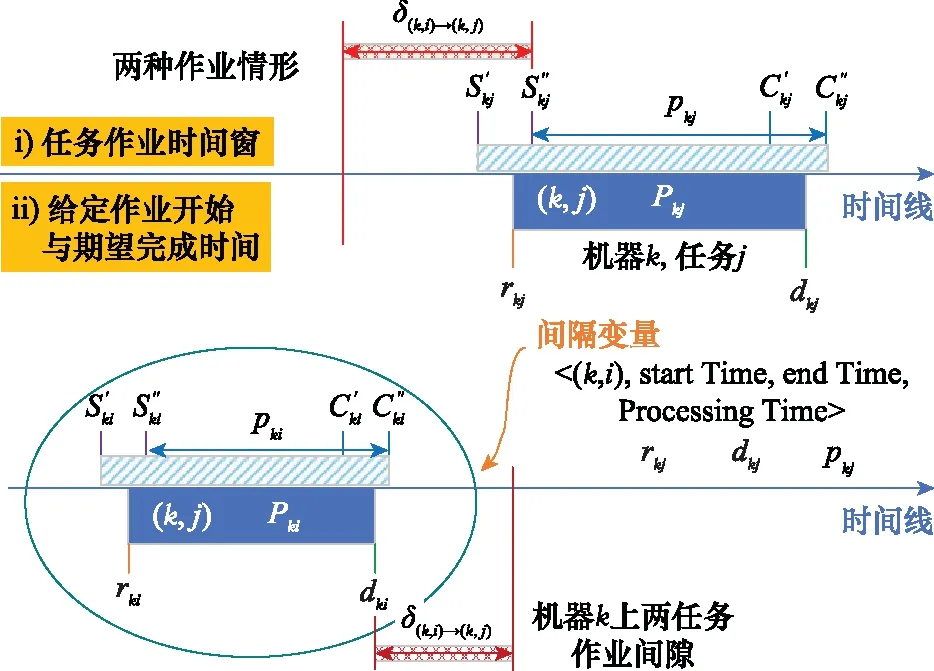
图4 同一机器前后任务作业间隔松弛间隙示意图Fig.4 Schematic diagram of slack clearance between task operation inteval before and after the same machine
约束规划采用的是约束满足技术,主要依靠约束传播算法[18]。做法是插入新的优先级约束(析取弧),而这个优先级约束隐含在之前插入的优先约束和调度问题的原始约束中。由于新优先级的插入,约束满足算法重新计算各作业的时间窗。而对于每对在同一机器上处理作业任务,编排中可能存在以下4种情况。
情形 1δ(k,i)→(k, j)≥0&&δ(k, j)→(k,i)<0,优先级约束为任务(k,i)→(k,j),表先后关系;
情形 2δ(k,j)→(k, i)≥0&&δ(k, i)→(k,j)<0,优先级约束为任务(k,j)→(k,i);
情形 3δ(k,i)→(k, j)<0&&δ(k, j)→(k,i)<0,排列中不存在这种调度方案;
情形 4δ(k,i)→(k, j)≥0&&δ(k, j)→(k,i)≥0,任务(k,i)→(k,j)或(k,j)→(k,i)均可,即二者无先后优先级要求。
3.1.2 调度设计编排规则
(1) 对于满足情形4的一对作业(任意排列均可)编排。如果出现多于1对满足情形4的任务对,那么需要采用搜索启发法进行编排。直接推理启发策略为:任务对的选择是基于该任务对所提供的排列灵活度进行的,具有最低灵活度的任务对则被选中。如果具有低灵活度的任务之前未调度好,那么在后面的编排中可能出现该任务对无法完成调度,所以低灵活度的任务对要比高灵活度的任务对优先编排。这里,灵活度依赖任务对(k,i)→(k,j)或(k,j)→(k,i)排列方案的松弛间隙大小。综上考虑,一种较为有效的任务对排序灵活度的评估策略可以是任务对排列的松弛间隙的均衡化处理:

(23)
式中:P((k,i),(k,j))为该任务对排序灵活度。
由式(23)知,如果任务对的松弛间隙最大值较大,则会拉高其排序灵活度,总体调度方案的编排优先级会延后。在P((k,i),(k,j))最低排序灵活度的任务对选中后,那么具有更大的松弛间隙的任务优先级则确定该任务对前后优先顺序,即δ(k, i)→(k, j)≥δ(k, j)→(k, i)⟹任务(k,i)优先于(k,j)。
(2) 对于满足情形3的一对作业的编排。当发生该情形时,调度方案将不能完成构建,算法需要回溯,即之前完成迭代计算的一个或多个排序决策将被取消;或者说,当前采用这种方式提出和构建的调度问题的解不存在,而且原问题部分约束还需要做进一步的松弛。
3.1.3 约束引导启发式(算法1)过程
步骤 1搜索初始化。
步骤 2计算每个未排序(调度编排)的任务对的松弛间隙,δ(k, i)→(k, j)和δ(k, j)→(k, i)。
步骤 3检查优先级约束条件,对需要排序(调度编排)的决策变量(任务对及其松弛间隙)进行分类。如果任意决策变量满足情形1或情形2,则进入步骤 4;如果任意决策变量满足情形3,则进行回溯;否则进入步骤 5。
步骤 4插入新的优先级约束,并进入步骤 2。
步骤 5如果没有决策变量属于情形4,则已找到调度可行解,算法1停止;否则进入步骤 6。
步骤 6对尚未排序(调度编排)的每个任务对进行排序灵活度P((k,i),(k,j))计算。选择minimumP((k,i),(k,j))的任务对,如果δ(k, i)→(k, j)≤δ(k, j)→(k, i),则任务(k,i)优先于(k,j);否则,任务(k,j)先于(k,i)。结束后返回步骤 4。
3.2 二分法算法迭代优化约束规划
约束规划问题的求解,是基于约束满足问题进行的。将目标函数最优值设定上界后,转化为约束条件并增加到模型约束当中,该FJSP问题的算法流程如下。
由图3及式(17)和式(20)可知,任务分配集有衍生约束,即工序、机器任务分配关系:
(24)
工序任务集Nj分配给该工序下可选机器完成,即机器任务分配一致性关联:
(25)
机器所分配任务具有前后关联关系,如分配机器1的任务与后续分配给机器4、机器7有前后约束关系。
设置目标函数下界L=z*=Cmakespan,Cmakespan为已知的一个目标下界(可以估计,其值的好坏直接影响算法效率),设置目标值上界U=Cmax(一个大常数),目标函数上下界中点值M=(L+U)/2。
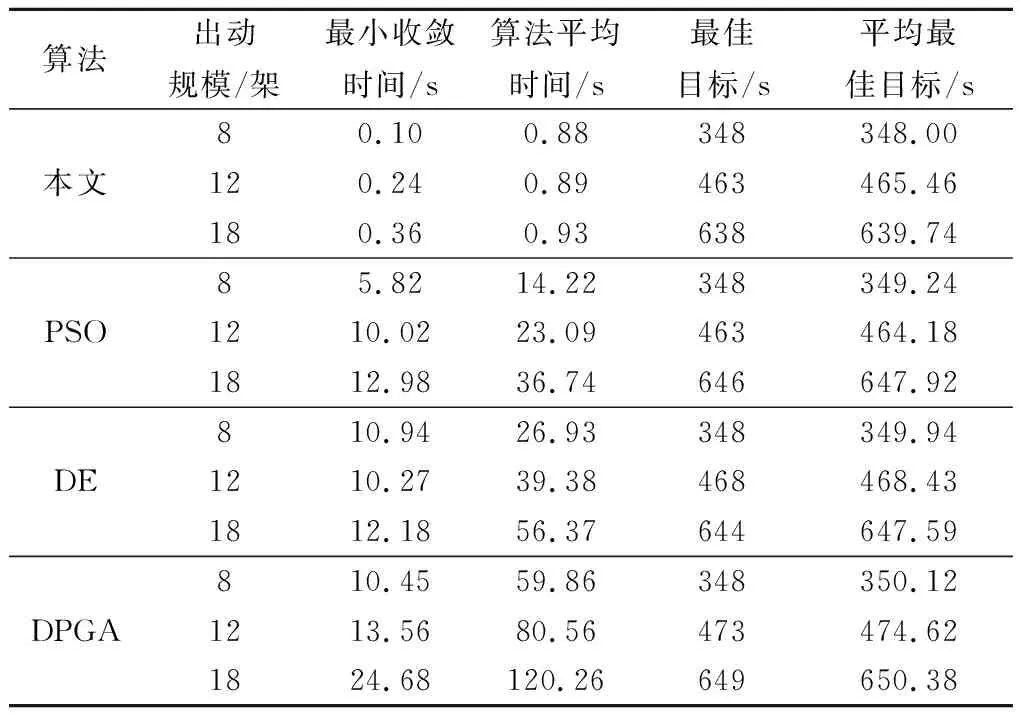
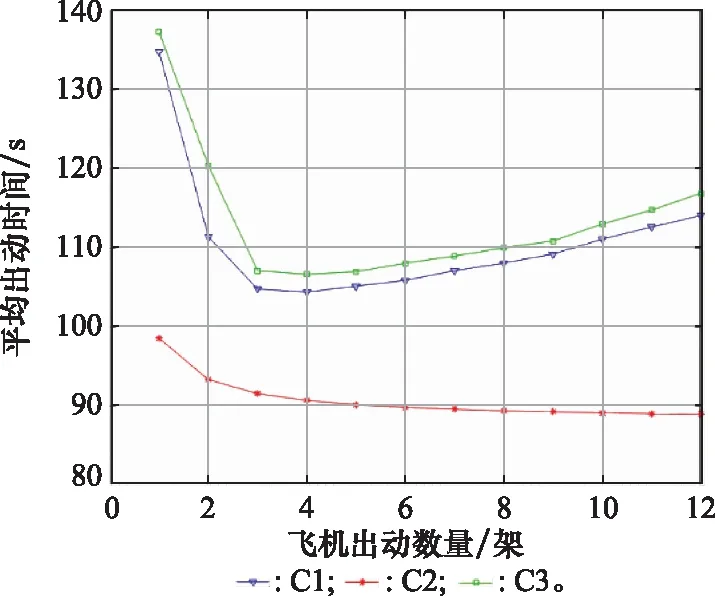
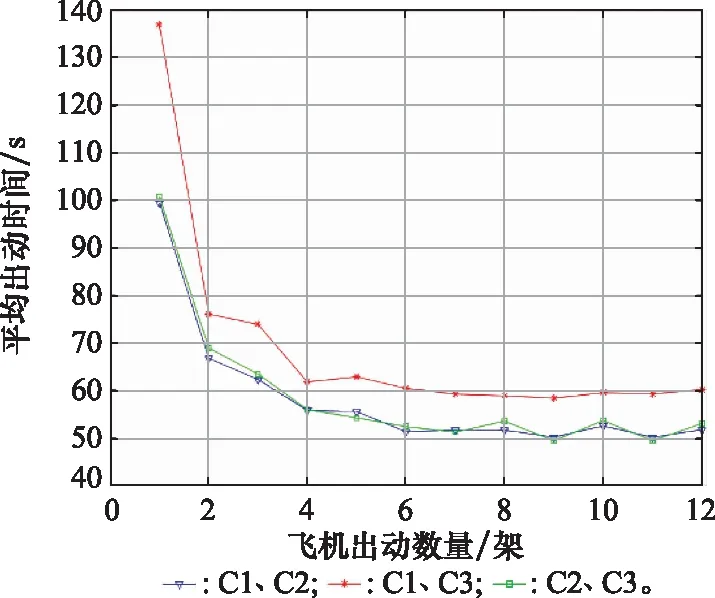
步骤 2启动二分法搜索优化。取k=1,新增约束g(ops(i,j.o))=g(mps(k,t.o)) 步骤 3机器任务集分配。如果k≤3,采用Monte Carlo模拟从机器k的可选任务集N1中生成任务集nk(见式(24))。此时,设置N1=N1-nk;如果3 步骤 4单机任务调度优化设计。对机器k所分配的任务集,生成一个操作序列,进行约束一致性检查(进行约束传播和领域缩减),使得调度方案满足约束式(21)要求。单机任务调度由约束引导启发算法完成,见算法1。完成该机器的任务分配与调度设计。 步骤 4.1如有可行解,机器k执行最后一个任务,zk=g(ops(i,j.o))=endOf(mps(k,t,o))(完成时间)。如果z*≤zk,则z*←zk;否则,z*←z*。 设置k=k+1,如果k≤10,返回步骤 3;否则,将新的上界设置为M,新上界记为U*=M,下界保持不变,新的中点M*=(L+U*)/2,二分法搜索进入步骤 5。 步骤 4.2如果无可行解,同新的下界设置为L*=M,上界保持不变,那么新的中点M*=(L*+U)/2,二分法搜索进入步骤 5。 步骤 5算法结束判定。当U*-L*>gap时,将M*值返回步骤 2,重新进行任务分配和调度设计;当U*-L*≤gap,算法停止。gap值为迭代计算时,目标函数的上下界值差。 说明二分法搜索在下界较优时效率很高,因为证明约束满足问题无可行解所需要的计算时间比较长,而找到约束满足问题的可行解相对简单。 图5 某型航母甲板概况图Fig.5 Overview of an aircraft carrier deck 本文仿真采用Matlab2018a+ILOG Cplex混合编程求解,运行环境Win10操作系统,Intel(R) i7-4790U CPU@3.6 GHZ处理器,内存8 GB。 图6为某一甲板态势下,选择8、12、18架飞机进行出动离场调度的算法仿真,左侧部分为飞机作业甘特图,如图6(a)所示,8架飞机中纵轴为各飞机编号,不同颜色块标定不同作业阶段(或工序),色块中编号代表机器号进行相应作业阶段加工,如M2-1对应纵轴第2架飞机表示该飞机第1阶段在机器2上处理,而其色块位置及跨度为起止时间,其他类推。右侧部分为机器作业甘特图,如图6(b)所示纵轴为加工机器号,不同颜色块由暗到亮依次表示不同飞机编号,色块编号则代表飞机的不同作业阶段,如J8-2对应纵轴机器6表示第8架飞机的第2个阶段在该机器上加工,同样色块位置及跨度代表起止时间和加工时间,其他类推。从图6中可以看出,各子图中的作业调度完成满足模型约束条件,各阶段及机器作业之间互斥兼容,不存在冲突情况,即给出方案完全可行,算法可以较好地解决离场调度设计。 图7是约束规划算法对不同出动规模的迭代计算过程,算法终止是结合gap值和约束满足检查次数进行的。横坐标是对迭代次数的抽样,纵轴为目标值,迭代目标值的更新策略是迭代中找到更好的满足解时进行,图7中各标星点为不同规模出动调度的约束满足解,并在标星点处记录其计算时刻,标识了算法收敛时间,及算法终止时间,计算中相关仿真结果如表1所示。从图7可以看出,算法对不同出动规模的最终收敛时间随着规模的增加而增大,依次为0.1 s、0.33 s、0.44 s,并呈现线性变化趋势。此外,不同规模算例的迭代结束时间也基本相当且小于1 s,即便不考虑其收敛点时间,算法的实时性较好。通过对初始数据各进行30次仿真,其结果均相同,说明算法较为稳定且较好地适应不同规模的调度计算。但如果不从最终收敛时间看,而调高gap阈值,仅关注目标值逼近到近似最优点,即图7中3条曲线0.05~0.06 s处“肘部”大转弯处结果。也就是说此时,算法对不同出动规模的调度计算在该“肘部”时间基本同时找到了近似最优解,而这个时间约为0.06 s。因此,如果退而求其次,当实际问题调度实时性要求高而仅需近似解,可以看出本文算法效率可满足要求,更重要的是对不同规模离场调度所需时间基本相同,而第4.3节将分析本文算法与其他经典方法的比较。 图7 不同出动规模下算法迭代收敛曲线Fig.7 Algorithm iteration convergence curves under different sortie scales 表1 不同规模飞机的出动调度仿真结果 而表1则列出算法对不同规模飞机的出动调度有关指标,算法性能在图7中作了阐述,其目标值分别为348 s、463 s及638 s,平均出动时间随出动规模的增加而减少,平均出动效率为35~44 s/架之间,这也基本符合实际出动情况,10.5 min内可将18架飞机在机务勤务保障完毕情况下完成放飞(而美国“尼米兹”级航母使用4个弹射位出动架次率约为28~30 s/架)。 实验数据是经合理化假定的,实际作业调度则可根据经验值进行修正,泛化到一般场景应用实现实时调度规划。仿真实验是基于作业时间确定、机器无故障且在给定离场数据进行任务规划,然而实际情况是作业时间具有随机性,机器可能故障,甲板滑行时可能因避碰检查带来的冲突隐患导致作业等待延迟。但是本文所设计算法依然有效,原因如下:一是针对实际作业不确定性问题,通过经验数据得到保守的期望作业时间,以此作为算法处理数据,并提供不同作业策略以适应不确定性[19],比如:① 调高期望作业时间来适应由海况环境变化导致甲板作业效率降低;② 在可能发生延迟时增加作业人力及配套设备给机器加工提速,进而弥补调度计划的作业偏差;③ 不可避免状况时整体向后偏移作业进程。二是针对机器故障发生时,若短时无法恢复,可捕获待调度信息启动算法的实时间重调度。 舰载机保障、出动、回收作业等各环节通常有明显分段特性,全周期作业优化可由各环节优化之累加,因此孤立分析出动离场的优化调度对现实意义明显。 针对调度问题,文献[5,7]给出了PSO、DLGA、DE等群体智能搜索算法,本文采样这些方法开展第4.1节算例条件下的仿真实验,初始化设置采取完全随机化与轮盘赌结合方式进行,种群规模为50,代数为500、100、500,参数设置:PSO中惯性权重0.9,加速因子(2,2);DPGA与DE算法中交叉与变异率均为0.1,仿真实验各做了30次,随机抽取各算法中的一次迭代收敛结果如图8所示。上述实验与本文算法结果性能比较如表2所示。图8给出的是出动规模为8架飞机时最优调度的迭代收敛曲线(其他情况类似),图8(a)中PSO算法经过较少迭代后便收敛,但算法随机性较大,最佳解获取为随机得到,该解相关信息并不能影响后续种群搜索,其最佳解获取之后的后续解质量较差;DPGA是种群整体演进优化,图8(b)中经过较少迭代后算法收敛,且算法后续种群总体上呈现收紧趋势,但是遗传机制无法解释该收敛值为全局最优,其实也是引言中谈到的算法早熟性(收敛快),容易限入局部最优;DE算法是GA的变种,图8(c)中算法经过较多的迭代后方才收敛,总体趋势是一个较为稳定的目标值收紧过程。显然上述智能算法同样也能较好解决调度优化问题,但实验中发现,上述方法在不同仿真实验结果往往会有差异、最佳目标值出现摄动,即算法的稳定性方面不够,或者说“最优”解的质量不足。 算法出动规模/架最小收敛时间/s算法平均时间/s最佳目标/s平均最佳目标/s本文80.100.88348348.00120.240.89463465.46180.360.93638639.74PSO85.8214.22348349.241210.0223.09463464.181812.9836.74646647.92DE810.9426.93348349.941210.2739.38468468.431812.1856.37644647.59DPGA810.4559.86348350.121213.5680.56473474.621824.68120.26649650.38 而表2中则给出了多次实验后上述方法与本文算法的区别比较,主要从收敛时间、算法平均时间、目标值波动等指标分析。单独从收敛时间看,本文算法远远优于智能算法,比DPGA或DE算法约提高近2个量级;而从算法平均时间看,本文算法同样也远好于上述智能搜索算法。各算法目标结果均具有一定的抖动,在小规模出动时目标值相对稳定,但随规模增大,智能算法的最佳目标值摄动更显著。尽管DPGA收敛的迭代次数比较少,但是最小收敛时间相比其他算法时间要多,各算法综合性能排序为本文fPSOfDEfDPGA。但是假如实际优化问题实时性计算要求较高时,要求在短时提供最佳解,即减少最大搜索迭代次数,那么此时PSO算法未必能好于DE算法,原因是算法稳定性方面不够好、随机性大。而DPGA效果因为双种群规模增大了搜索复杂度,降低了算法效率。 舰载机起降作业受航母甲板有限空间约束,所装配的弹射器和起飞位数量对于机群出动离场效率具有较大影响[20]。在本文规划模型和约束规划算法分析和仿真基础上,研究不同可用起飞位对不同规模飞机出动效率的影响规律。下面将对1~3个起飞位可用的情况下,不同规模飞机的平均出动时间进行计算(出动效率)。 (1) 1个起飞位可用的情况分析 航母有3个起飞位,分别假设只有C1或C2或C3起飞位可用情况下,计算不同规模飞机出动的平均时间。为确保计算结果的准确性,相同规模飞机出动时间计算,取不少于10种不同停机位飞机的出动组合方案求其均值作为该出动规模下的出动时间。那么可得到只有1个起飞位可用的情况下,出动1~12架飞机的平均出动时间变化情况如图9示。 图9 一个起飞位可用时平均出动时间与出动规模关系Fig.9 Relationship between average sortie time and sortie scale when one takeoff position is available 可以看出,相对而言C1和C3起飞位可用时,平均出动时间在4架处为最小,往后稍有增多;C2起飞位则随出动规模的增大而减少。因此,只有一个起飞位可用时,需要尽可能确保C2可用,然后是C1和C3。 (2) 2个及3个起飞位可用的情况分析 2个、3个起飞位可用时分析同上。当2个可用时,有C1与C2,C1与C3,C2与C3 3种组合,同上方法,那么1~12架飞机的平均出动时间变化情况如图10示。可以看出,出动规模超过4架以上时,其平均出动时间基本保持在50~65 s之间,C1、C2及C2、C3这两组均与C2的组合出动效率相当,优于C1、C3的组合。因此,C2起飞位非常关键,起到拉低平均出动时间作用,保持其功能完好对提高出动效能意义重大。而3个起飞位均可用时,第4.2节中已给出仿真分析,这里不赘述。 图10 两个起飞位可用时平均出动时间与出动规模关系Fig.10 Relationship betwween average sortie time and sortie scale when two takeoff positions are available 综上分析,基于弹射起飞的出动离场调度优化问题,在起飞位不能同时使用情况下,合理使用C2起飞位并确保其性能完好对出动效率的提升意义重大。仅使用一个起飞位时,C1、C3起飞位对出动效率贡献性能相当,但是C2起飞位效果理想;有两个起飞位时,出动效率随出动规模增加到6架以上时将稳定在60 s/架左右。本文研究的是弹射起飞模式,相较于俄“库兹涅佐夫”的滑跃起飞,出动效率在相同出动情况下可以提升约20 s/架。 本文对舰载机出动离场问题抽象成FJSP模型来进行调度优化研究。一是模型建立。在传统数学规划模型的基础上进行适当调整,引入易于直观理解的调度逻辑约束和时间间隔决策变量,建立了对应的约束规划模型。二是约束规划模型算法。运用调度分解技术将调度问题划分为多个单机调度的组合优化问题,最终通过约束规划的二分法迭代算法完成优化问题收敛,而将其单机调度为任务分配和调度设计两个阶段完成,任务分配由Monte Carlo模拟生成,调度设计则由约束引导启发式搜索算法完成。三是对比实例仿真分析。将约束规划算法与传统群体智能算法比较分析发现,在本文所研究的中小规模调度优化问题中,前者算法效率比后者提升约2个数量级。当然,由于约束规划其实也利用类似分枝定界的树搜索算法,最大的改进是利用约束传播和领域缩减技术极大减少搜索空间,通过对不同出动规模的仿真发现,算法效率非常高且随着规模的增加算法时间呈线性增长趋势,当然规模的增加成超大型规模后算法时间将会出现爆炸式增长,而这不属于本文研究范围。因现实的出动离场问题均属于中小型复杂约束问题,要求的就是实效性及在线规划性能,那么从这点来讲,约束规划便能很好地解决此类问题。四是对3个起飞位可用情况进行对比分析。起飞位使用越多出动效率越高,仅1个起飞位可用时,C2效能最高,C1、C3相当,出动时间约100 s/架;仅2个起飞位可用时,含C2组合的效能较高,C1和C3组合效能较差,出动时间约60 s/架;当3个起飞位均使用时,平均出动效率约为40 s/架。因此,C2起飞位对出动效能的贡献度最大,实际使用时应尽可能最大程度确保其可用性、可靠性。此外,出动效率随出动规模的增多而增大,但一定规模后趋缓或少量降低。4 仿真分析
4.1 仿真初始条件
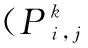

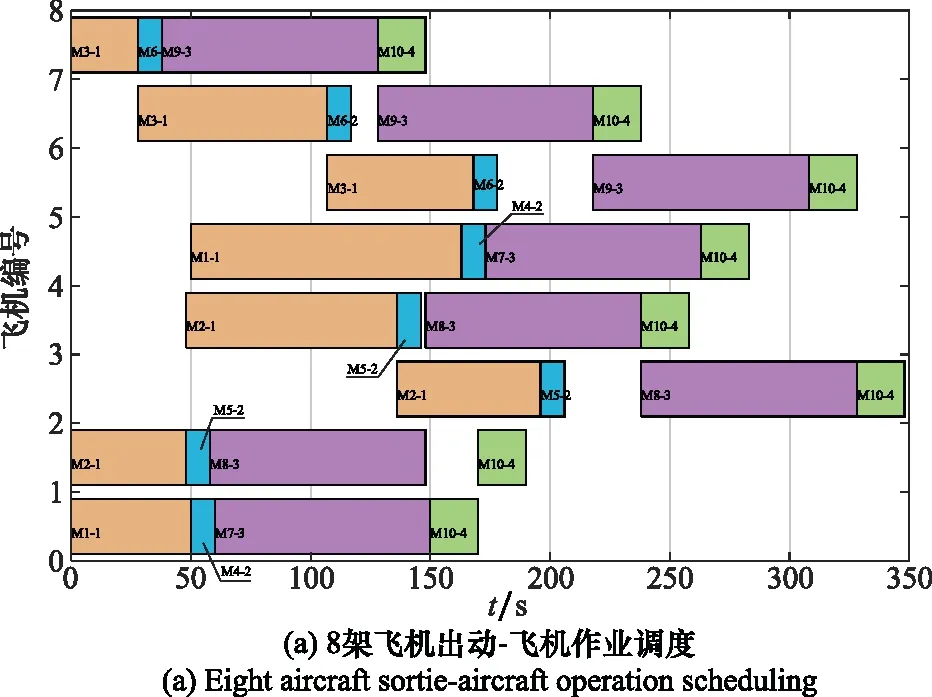
4.2 算例实现与结果分析

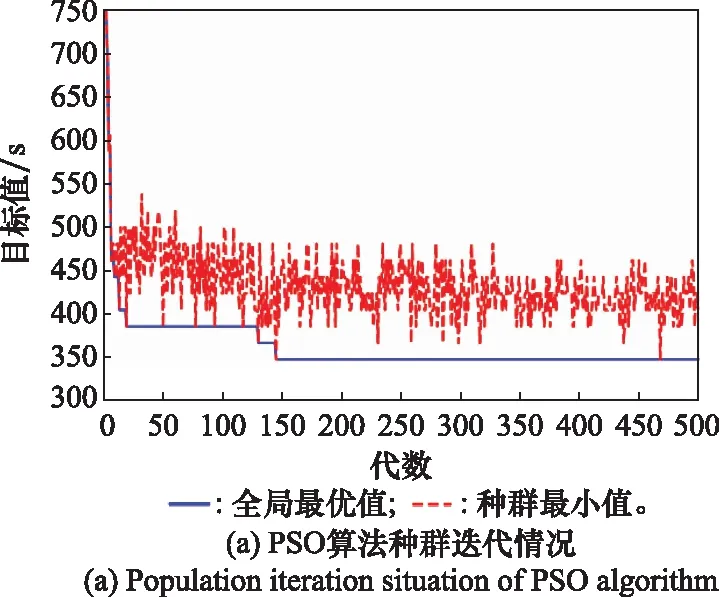
4.3 约束规划算法与经典算法的比较
4.4 模型灵敏度分析
5 结 论
