基于FMCW雷达的旋转目标微动参数提取方法

冯维婷, 梁 青, 谷 静

(西安邮电大学电子工程学院, 陕西 西安 710121)

0 引 言

在雷达目标中有一类是旋转目标,比如无人机旋翼的旋转,弹道中段目标的自旋、锥旋,这一类目标除质心平动以外内部旋转的局部运动称为微动[1-3]。无人机处于悬停状态时的微动特征是识别目标或干扰的重要依据,弹道中段目标的自旋、锥旋特征也是区别于诱饵和欺骗干扰的重要特征。因此,对旋转目标微动特征的提取分析一直是雷达目标识别领域的研究热点[4-5]。

雷达目标的微动会调制雷达回波相位,使得目标主体平动引起的多普勒频率周围产生调制边带,这是微多普勒效应[6]。对微多普勒参数的提取方法中,文献[7-8]采用参数化提取方法,基于目标的微动特征构造包含若干个参数的解调算子对信号进行解调,若干个参数在多维平面上进行搜索,当合适的参数构成的解调算子与信号匹配时解调信号能量最大,从而通过搜索峰值进行目标微动参数的估计。参数化方法是多维搜索方法,参数估计精度取决于搜索步长,高精度的参数估计值必然有巨大的运算量。

微多普勒频率具有时变特征,大量的文献利用时频分析方法处理这类非平稳信号。文献[9]对时频分布结果采用经验模式分解方法将时频曲线分解成若干独立曲线来估计目标的微动参数,但经验模式分解方法存在模式混叠问题,无法有效处理复杂的雷达信号。文献[10]计算信号的时频分布,基于时频脊线分离出各散射点的时频曲线来取得目标微动参数,然而存在相互交叠处的时频脊线提取错误问题。为了解决多条时频曲线相互交叠难以提取的问题,文献[11]结合时频分布与逆Radon变换进行微动参数估计,逆Radon变换需要提前知道时频曲线的周期,文中采用自相关法进行周期估计,但自相关法适合单分量信号,无法有效估计多分量的信号周期。

针对以上问题,以旋转目标微动参数提取为研究对象,利用德州仪器公司的60 GHz频段调频连续波(frequency modulated continuous wave, FMCW)毫米波小型雷达系统IWR6843搭建实验平台,进行旋转目标雷达实测数据的采集。从FMCW雷达接收到的回波信号出发,分析了旋转目标微多普勒信号特征、利用奇异值比谱、时频分析和逆Radon变换相结合的方法进行雷达采集数据的分析,完成了旋转目标微动参数的有效估计。

1 FMCW雷达微动参数特征分析

1.1 雷达信号模型

雷达发射宽带线性调频信号,在一个调频周期内,发射信号的解析表达式为

(1)

式中:t表示一个调频周期TC内的快时间;AT表示信号振幅;fc表示信号载波频率;K表示信号调频斜率。经时延τ后,雷达接收的回波信号表示为

(2)

式中:AR表示接收信号振幅;时延τ=2d/c,其中d表示雷达与目标之间距离,c表示光速。

sR(t)与sT(t)混频处理,再经过低通滤波器,得到的中频信号表示为

sIF(t)=AIFexp[j2π(fcτ+fIFt)]

(3)

式中:AIF表示中频信号振幅;fIF表示中频信号频率;fIF=Kτ。fIF与距离d的关系为

(4)

式中:B表示信号带宽。由于TC很小,一个TC内的距离近似为常量,因此对式(3)进行频域分析估得fIF,再利用式(4)可以得到目标距离。

FMCW雷达连续发射多帧信号,每帧有多个线性调频信号,对多帧中频信号需要考虑目标运动引起的多普勒现象,离散化后的多帧中频信号可以表示为

sIF(n,m)=AIF(n,m)·exp{j2π[fIFn+fd(m)n)]}

(5)

式中:n表示快时间离散序列,长度为N;m表示慢时间离散序列,长度为M;fd是距离变化引起的多普勒频率。

为了获取旋转目标的微动参数,对式(5)在每个TC进行脉冲压缩,脉冲压缩结果中目标所在距离单元对应的M点信号就是包含多普勒频率的雷达多普勒信号。

1.2 旋转目标微动特征分析

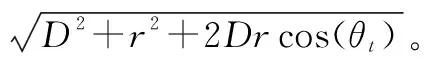
图1 雷达与旋转目标几何关系示意图Fig.1 Diagram of geometrical relationship between radar and rotating target

当旋转目标满足远场条件,即(r/D)2→0,雷达与旋转散射点P的距离可近似为

dP(t)≈D+rcos(2πfrt+θ0)

(6)

对式(6)求导得目标速度为v(t)=d/dt[dP(t)]=-2πrfrsin(2πfrt+θ0)。根据fd的定义,旋转目标的微多普勒频率可以表示为

(7)

式中:λ为载波波长。

由式(7)可见,旋转散射点P的微多普勒频率是随时间按正弦规律变化的曲线。正弦曲线的频率就是目标的旋转频率fr,初始相位就是散射点P在观测初始时刻的相位θ0,振幅即是最大微多普勒频率,该值由旋转半径、旋转频率和载波波长共同决定,包含了目标的结构信息。一般情况下绕固定中心旋转的散射点有多个,它们具有相同的旋转频率fr、不同的旋转半径和初始相位,Q个旋转散射点的多普勒频率可以表示为

(8)

可以看出,同一旋转中心的多个散射点,其微动特征表现为微多普勒频率是一组频率相同的正弦信号的叠加,各正弦信号的振幅和初始相位不同。因此,旋转目标微多普勒频率中各正弦信号振幅、频率和初始相位3个参数的提取是检测和识别不同旋转目标的基本依据。

2 微动参数提取方法

根据第1节结论,旋转目标微动参数包括旋转频率fr、初始相位θ0和包含在最大微多普勒频率中的旋转半径r。为了提取微动参数,采用的方法主要有3部分:基于奇异值比谱的旋转频率估计、时频分析技术和利用逆Radon变换的振幅和初始相位估计。

2.1 基于奇异值分解的旋转频率估计

雷达脉冲压缩后的多普勒信号表示为s(m),m=1,2,…,M。用信号s(m)构造矩阵A,其表达式表示为

(9)

式中:Mj、Mi是正整数,Mj·Mi≤M。对A进行奇异值分解[13]

A=UDVT

(10)

式中:U为Mj阶矩阵,U的列为A·AT的正交特征向量;V为Mi阶矩阵,V的列为AT·A的正交特征向量;D为Mj×Mi的对角矩阵,对角线上前z个非零元素称为奇异值,表示为σi(i=1,2,…,z)。

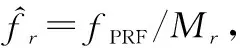
实际上基于式(9)构造的矩阵A存在假设周期与实际周期之间的截断误差不断积累的问题,常常无法有效估计频率。受到周期信号奇异值分解特点的启发,改进矩阵A的构造方法。重新构造的矩阵A为

(11)

式中:Mk=[k·fPRF/fri],符号[·]表示取整,fri是旋转频率在一定估计范围内进行搜索的第i次值,搜索范围表示为[frmin,frmax];L=[fPRF/fri]。

对每一个fri,进行式(11)构造的矩阵A的奇异值分解,计算奇异值比谱SVR(fri),旋转频率估计范围[frmin,frmax]的峰值处对应频率就是fr的估计值。

2.2 基于同步压缩变换的时频分析

时频分析技术是分析非平稳信号的有利工具,可以得到微多普勒频率随时间变化规律。这里采用同步压缩变换(synchro-squeezing transform,SST)的时频分析技术。SST以短时傅里叶变换(short time Fourier transform,STFT)为基础计算信号的线性时频谱,再进行压缩,最后输出分辨率高于STFT的时频谱[15-16]。信号s(t)的STFT定义为

(12)

式中:g(τ-t)代表随t移动的窗函数。用一定长度的窗函数g截取信号s(t),对截取信号进行傅里叶变换得到t时刻信号的局部频谱信息。随着窗函数g沿整个时间轴的移动,就得到了信号在整个时间-频率轴上的完整频谱分布。

对于谐波信号sk(t)=ej2πfkt,经STFT后的时频谱能量集中在以频率值fk为中心的一定频带宽度内,并且其两侧的时频系数随着与fk的距离增大而减小。由于窗函数的截断效应,信号的时频谱存在模糊,时频分辨率较低。

为了提高时频分辨率,SST基于STFT进行瞬时频率fI(t,f)的估计[17],表达式为

(13)

(14)

2.3 基于逆Radon变换的微动参数提取

对旋转目标的多普勒信号进行时频分析,微多普勒频率表现为时频谱图中多条同频率的正弦曲线的叠加,各曲线之间相互交叠。传统的微多普勒参数提取方法是通过检测时频谱的能量峰值,提取出各条时频脊线完成参数估计,但是相互交叠的曲线在交叉点处容易检测到错误曲线,导致方法失效。为了解决时频曲线难以提取的问题,根据旋转目标微多普勒频率的正弦形式特点,采用逆Radon变换提取正弦信号的振幅和初始相位两个参数。

逆Radon变换能对时频谱图中的正弦曲线进行能量积累、聚焦,将微动参数估计问题转化为逆Radon变换后参数空间中的峰值检测问题。

旋转散射点P的微多普勒频率重新写成如下形式:

fd(l,θ)=δ(l-lPsin(θ+θ0))

(15)

式中:lP是正弦信号的振幅,与式(7)的对应关系为lP=4πrfr/λ,即最大微多普勒频率;θ是随时间变化的旋转相位,θ=2πfrt。

时频平面上fd(l,θ) 的逆Radon变换[19]为

g(x,y)=

(16)

式中:kx=ηcosθ;ky=ηsinθ。

Q个散射点逆Radon变换结果为

(17)

由式(17)可知,时频平面上的一条正弦曲线经逆Radon变换后是x-y参数空间中的一个点(xi,yi),该点对应于正弦曲线的振幅lPi和初始相位θ0i。lPi与θ0i估计值与点坐标(xi,yi)的关系为

(18)

进行逆Radon变换前需要已知各正弦曲线的周期,其值根据上文中改进的奇异值比谱方法得到。

综上,多个散射点的微动参数估计具体算法过程如下:

步骤 1将接收到的雷达中频信号存放为二维数据矩阵形式,每行是一个调频周期的N点快时间信号,每列是M个调频周期构成的慢时间信号。

步骤 2对快时间维进行脉冲压缩得到距离维信息,抑制静止目标、干扰和噪声,取出旋转目标所在的若干个距离单元并进行相加,得到目标慢时间维的M点多普勒信号。

步骤 3用多普勒信号构造矩阵A,并进行奇异值分解,见式(10)和式(11),基于奇异值比谱并搜索峰值估计旋转频率fr。

步骤 4对多普勒信号计算SST时频谱,对时频谱图进行逆Radon变换,估计最强目标分量的旋转半径和初始相位。

步骤 5利用估计值构造最强分量信号,将其从原多普勒信号中剔除。

步骤 6重复步骤4和步骤5,直到估计出所有分量信号参数为止。

算法的处理流程如图2所示。

图2 算法流程图Fig.2 Flow chart of the proposed algorithm

3 实验结果

3.1 仿真分析

选取3个旋转散射点进行仿真,雷达波长为0.005 m;多普勒信号的振幅为1;散射点的旋转频率为4.5 Hz;各散射点的旋转半径为r1=0.10 m,r2=0.15 m,r3=0.20 m;初始相位为θ01=0.780 rad,θ02=2.870 rad,θ03=4.970 rad。设置高斯白噪声下多普勒信号的信噪比(signal to noise ratio,SNR)为0 dB。

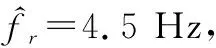
图3 奇异值比谱Fig.3 Singular value ratio spectrum

多普勒信号的STFT和SST时频谱如图4所示。

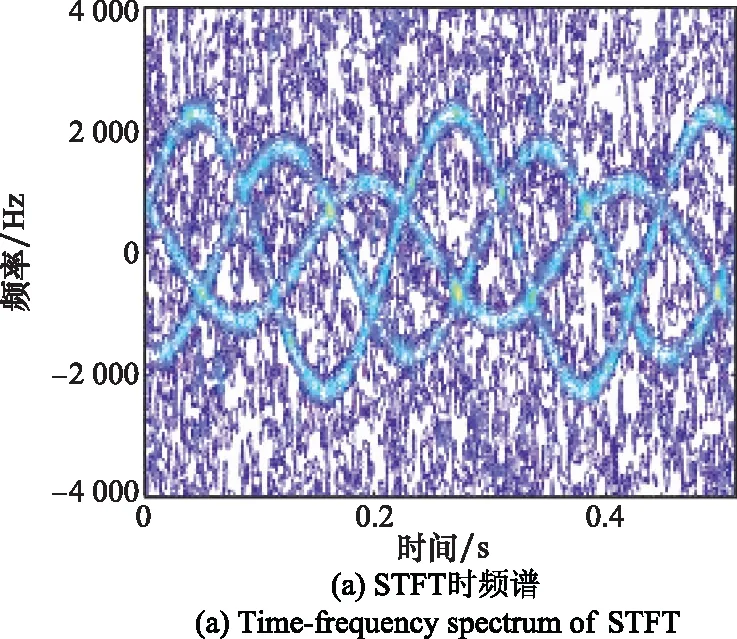
由图4可以看出,时频谱中3个旋转散射点微多普勒频率为标准的正弦曲线形式,各曲线相互交叠,曲线的频率相同,振幅和起始相位不同。图4(a)的STFT时频谱时频聚集性较差,频率分辨率较低。图4(b)的SST时频谱谱线清晰,时频分辨率较高。

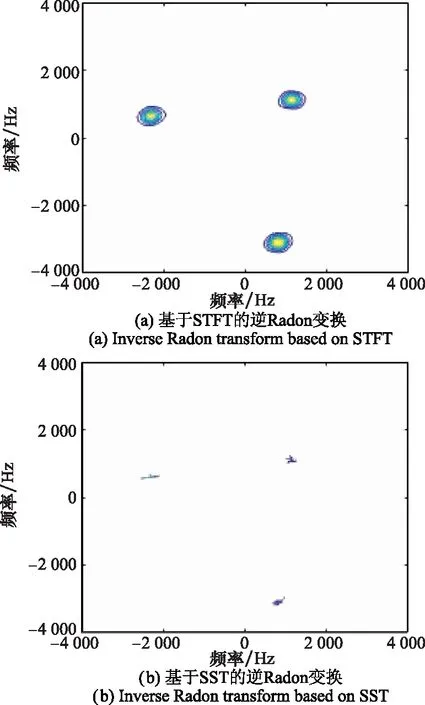
图5 逆Radon变换结果Fig.5 Inverse Radon transform

采用所提方法在SNR分别为-6 dB、-3 dB、0 dB、3 dB、6 dB时,各进行100点蒙特卡罗实验,得到旋转频率的估值均为4.5 Hz, 3个散射点的旋转半径和起始相位平均估计值见表1和表2。由表1和表2可以看出,各参数估计误差随着SNR的增加而减小,并且在强噪声环境下所提方法仍能得到旋转半径和起始相位的高精度估计值。

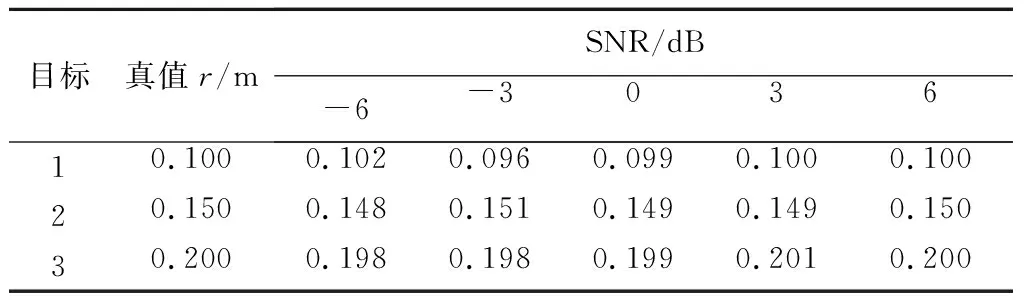
表1 旋转半径估计值

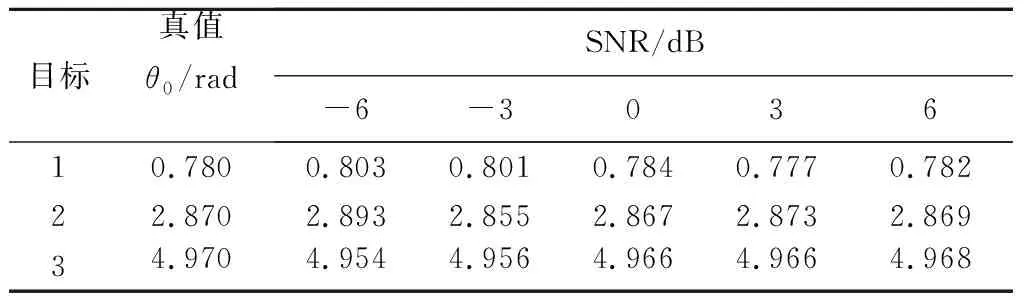
表2 起始相位估计值

3.2 实测实验

实测实验使用的FMCW雷达是德州仪器公司的IWR6843毫米波雷达系统,配置了DCA1000高速数据采集卡,采用1发4收模式采集信号。试验中雷达参数设置如下:载波频率fc=62.5 GHz,采样频率FS=2 MHz,调频斜率K=25.998 MHz/μs,一帧数据包含128个调频周期数,调频周期TC=240 μs,一个调频周期内的采样点数为256点,实际带宽B=3.328 GHz,脉冲重复频率为3 200 Hz。

实测实验装置如图6所示,设置的转台中心与雷达之间的距离约1.2 m, 旋转半径约0.14 m,两个旋转目标的相位差为π rad。

图6 实验装置Fig.6 Experimental devices

接收到的雷达中频信号中取一帧数据,首先对每个调频周期的256点快时间信号进行脉冲压缩得到一维距离像,再对一帧数据的128个调频周期数据在慢时间维进行傅里叶变换得到距离-多普勒像。一帧实测数据的距离-多普勒像如图7所示。

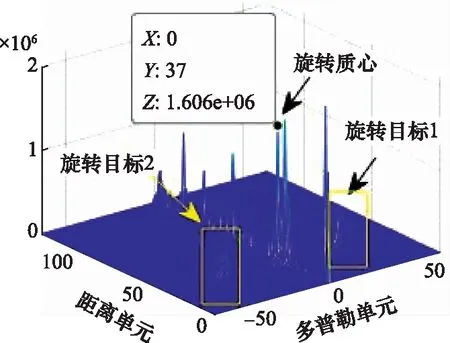
图7 一帧数据距离-多普勒像Fig.7 Range-Doppler imaging of one frame’s data

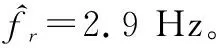
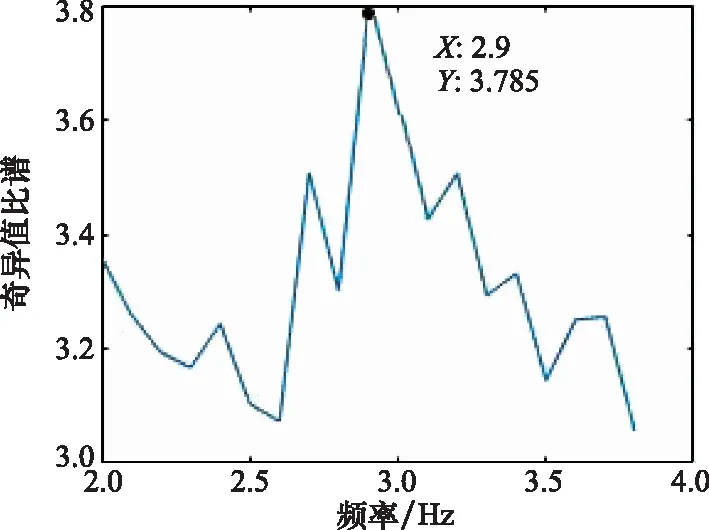
图8 奇异值比谱Fig.8 Singular value ratio spectrum

对实测实验数据进行SST变换,时频分析结果如图9所示。

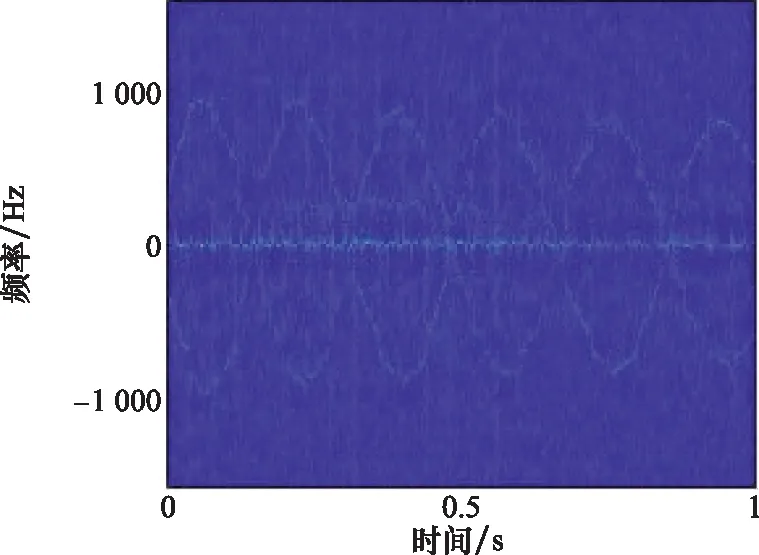
图9 旋转目标SST时频谱Fig.9 SST time-frequency spectrum of rotating targets

图9的时频谱中是两条相位相反的正弦曲线,这与图6的实验设置相符。图中零多普勒频率对应的转盘主体能量大于两个散射点的能量,不利于微动参数提取。对多普勒信号求导处理,消除强零频干扰,而两个散射点的微多普勒频率波形基本不受影响,求导处理后的时频谱如图10所示。

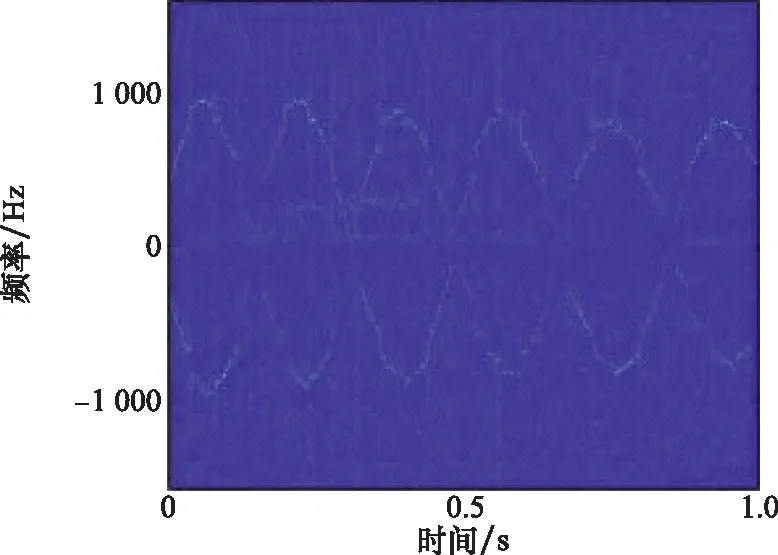
图10 求导处理后的SST时频谱Fig.10 SST time-frequency spectrum after calculation of derivation

实测实验数据的逆Radon变换结果如图11所示。

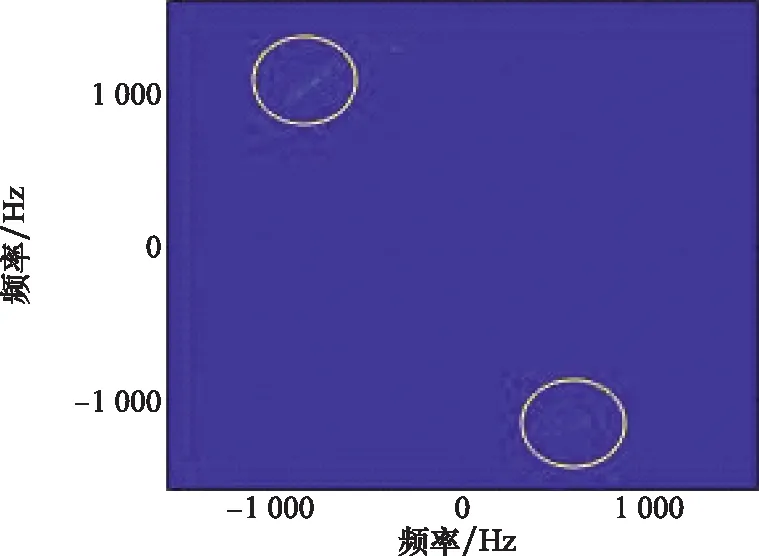
图11 逆Radon变换结果Fig.11 Inverse Radon transform

图11中逆Radon变换结果存在展宽现象,这是因为图10中的时频曲线并非理想等幅的标准正弦曲线的缘故。

2个旋转目标的微动参数平均估计值见表3。实际旋转目标的初始相位和旋转频率未知,但从表3的旋转半径估值与真值的对比可以看出旋转半径的估值与真值基本符合;虽然初始相位未知,但是2个旋转目标的相位差是确定的,相位差的估值与真值也基本符合;旋转频率的估值是其他微动参数估计的基础,其他微动参数的有效估计间接表明了旋转频率估值的有效性,因此所提方法能有效估计实际雷达旋转目标的微动参数。

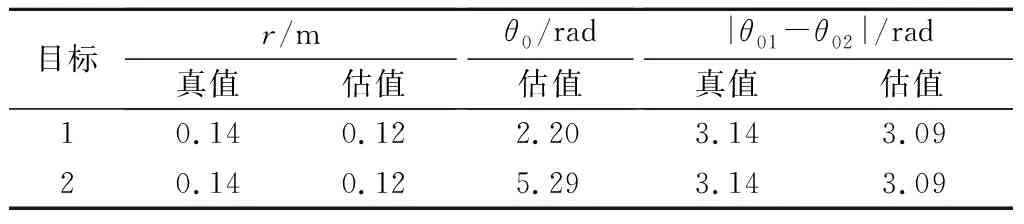
表3 实测数据微动参数估计值

4 结 论

以旋转目标为研究对象,基于FMCW雷达推导了其多普勒信号的解析形式,并根据信号时频谱的正弦曲线特征,提出了综合利用奇异值比谱、SST时频分析技术和逆Radon变换以提取旋转目标微动参数的方法。仿真分析和雷达实测数据的实验结果表明,所提方法能有效提取旋转目标旋转频率、旋转半径和初始相位值,算法抗干扰能力强,参数估计精度较高,所得的微动参数为后继的雷达目标分类、识别、监测打下了基础,也为复杂背景中复杂雷达目标微动特征分析提取提供了一种途径。