基于PSO-CNN的LPI雷达波形识别算法

赵 帅, 刘松涛, 汪慧阳

(海军大连舰艇学院信息系统系, 辽宁 大连 116018)

0 引 言

低截获概率(low probability of intercept, LPI)雷达是一种基于脉冲压缩技术实现信号高时宽带宽积、强抗干扰能力及低截获特性的新型雷达,现广泛装备于各国军队。在当今复杂电磁环境、激烈电子攻防及信息制胜的战场背景下,准确高效识别对抗方的LPI雷达波形,对判断危险等级、构建战场态势及实施对抗干扰和干扰效果评估具有重要意义[1]。

基于时频分析的LPI雷达波形识别方法是该领域的重要分支。作为结合了时间与频率分析手段的信号处理方法,该方法能够更准确地反映雷达信号这种非平稳信号的时变本质,使得对雷达信号的分析精确到具体时间的特定频率上,具有对雷达信号的惟一可辨识性。时频分析算法种类繁多,常见的有STFT(short-time Fourier transform)、WT(wavelet analysis)、CWD(Choi-William distribution)、WVD(wigner-ville distribution)及其变种等。该类方法首先将雷达信号转变为时频图像,后对图像进行识别来实现对雷达信号的分类。

卷积神经网络(convolution neural network, CNN)在图像识别领域有着举足轻重的地位。在对雷达时频图像识别的研究中,CNN作为主流的特征提取及分类器被广泛应用,如何选取适配高效的CNN结构成为学者们亟待解决的问题。Zhang在文献[2]中对CNN的卷积层数量、隐藏单元数量及池化层种类进行人工选参,通过对比确定出最为适合的网络超参数,并将其应用于8种LPI雷达波形的识别中。Kong则在固定卷积层数量、种类的基础上对网络输入尺寸、卷积核数量及大小进行了对比实验,得到了其实验范围内最适于12种LPI雷达识别的超参数[3]。吴琼在其硕士毕业论文中细致讲述了应用于雷达波形识别的多种CNN改进办法[4]。上述文献均是依靠人工设置多组CNN超参数,依次训练对比结果择优,缺乏智能性及客观性。

于是,本文思考是否可以选取一种优化算法,与CNN相结合自适应智能选定最优CNN网络结构,以实现更好的LPI雷达波形识别效果。

在优化算法与CNN的结合领域,国内学者的研究多是在固定的网络结构上,使用优化算法代替传统的梯度下降法更新网络连接权值或阈值。如杨洁改进遗传算法的适应度函数及交叉算子,将其应用于反向传播(back proportion,BP)神经网络的初始权值与阈值的寻优[5]。赵毅提出一种改进的量子粒子群优化(particle swarm optimization,PSO)算法,并将其与CNN结合[6]。此外还有高华照构建的FC-VGGNet-plus+PSO模型[7],王金哲提出PD-CNN(PSO+Dropout,PD)算法[8],均是对CNN权值、阈值进行优化。这些研究尽管在一定程度上提高了CNN的识别效果,但并未解决网络优化的焦点问题,即结构寻优。

优化网络结构方面,白燕燕在固定CNN网络层数、类型排列的前提下,将卷积层中核的大小及数量、池化层类型、激活函数类型、训练批量及学习率作为PSO粒子分量,迭代寻找最适于手写体数据集的CNN结构[9]。该算法表现出了一定的先进性,但仍未摆脱既定网络层架构前提这一桎梏。国外学者Junior提出一种psoCNN算法[10],可自动搭建不定层数的CNN网络,该算法将CNN视作PSO的一个粒子,设置网络训练损失为适应函数,结合设置的CNN粒子更新机制,自动寻找最优CNN结构,但该算法设定的网络排列原则还有欠缺,易生成不合理的网络结构,且算法评估指标单一,可调整性、适应性有待提高。

结合并设计改进Junior的psoCNN算法思想,本文提出一种基于PSO-CNN的LPI雷达识别算法,以解决该方向主流分类器CNN的框架寻优问题,可为未来该领域CNN的选定提供参考。

1 CNN

CNN[11]作为一种前馈神经网络,通过局部连接和权值共享大大缩减了参数数量,同时其二维形式可以很好地表征图像像素之间的内部联系,这些优点使得CNN在图像处理领域大放异彩。

CNN主要由3种类型的网络层堆叠而成,即卷积层(conv)、池化层(pool)和全连接层(FC)。每一层的输出为该层输入与层内权值、偏置的函数值,该函数通常称为激活函数。CNN的训练过程由双向传播构成。在数学层面,CNN前向传播可表示为

(1)

式中:X为输入数据;Oi为第i层的输出;fi(·)为第i层使用的激活函数;gi(·)为第i层进行的加权运算;Zi为该层的加权运算输出;Wi与b分别表示该层的权值与偏置。对于3种不同的网络层,gi(·)有着不同的形式,具体如下所示:

(2)

式中:⊗表示卷积层输入与层内权值进行的卷积运算;Pooling(·)表示池化层进行的下采样操作,包括平均池化和最大池化两种,主要用来缩减输出参数量;如果是全连接层,则进行内积运算。

CNN前向传播输出预测值,通过误差函数衡量其与标签值之间的差异,随后反向传播使用梯度下降法更新网络权重最小化误差函数。CNN训练的过程也是最小化误差函数的过程。常见的误差函数有交叉熵及均方误差(mean squared error, MSE)。

作为一种深层有监督神经网络,训练一个完整的CNN网络需要大量时间,对多个CNN的试错择优将更为花费时间且寻优范围十分有限。因此,设计一种能够尽可能快的大范围自动构建并评估寻优CNN架构的算法尤为重要。

2 PSO算法

PSO算法是一种典型的群智能优化算法[12],模拟鸟群随机搜寻事物的捕食行为而得来。将优化问题的潜在解比作搜索空间中的一只鸟,称其为“粒子”。“粒子”在迭代过程中依照式(3)及式(4)更新其速度和位置。PSO算法流程如图1所示。

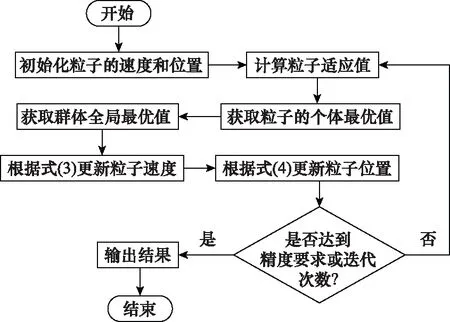
图1 PSO算法流程图Fig.1 Flow chart of PSO algorithm

粒子i的第d维速度更新公式:

(3)

粒子i的第d维位置更新公式:

(4)

剖析式(3)等式右边的3部分:第1部分为惯性部分,即粒子维持先前运动状态的趋势;第2部分为认知部分,即粒子通过记忆逼近自身历史最佳位置的趋势;第3部分为社会部分,即粒子通过共享经验逼近群体或邻域历史最佳位置的趋势。

PSO搜索范围广、参数数量少、收敛速度快,且算法实现易[13-14],十分适用于复杂耗时的CNN寻优工作。

3 基于PSO-CNN的波形识别算法

3.1 PSO-CNN整体算法

将CNN的一种结构视作PSO的一个粒子,每个粒子由离散的网络层功能块组表示,例如:conv|avgpool|conv|maxpool|FC。粒子训练、测试、评估时,直接对功能块组进行编译。CNN粒子训练过程的评估指标(grade),即适应度函数由两部分构成:一是识别精度,由训练过程中的验证准确率(acc)衡量;二是网络复杂度,由网络参数量(Np)衡量。两部分可通过权重因子Cf调整所占比重,具体构成如下:

(5)

式中:Nb为基准网络参数量。选取当前个体与全局grade最高的CNN粒子作为pbest与gbest。不同于传统粒子更新方式,粒子并非为数值表示,因此连续域数值累积的更新方式需转变为离散功能块的增删替换,粒子群初始化、粒子速度的计算及粒子的更新也需新的机制。

PSO-CNN算法的整体框架如算法1所示,其中涉及的粒子群初始化、粒子速度计算与更新分别由第3.2和第3.3节介绍。对于CNN粒子识别精度的评估,可选取网络训练时的训练验证准确率及测试集测试准确率作为评估依据。为压缩整体训练时间,本文所设定的粒子评估前训练epoch数通常较小,这时使用测试集测试的准确率通常不高,并不能有效衡量粒子质量,而网络训练时的验证准确率可在训练前期选取出具有最优潜力的粒子,因此使用验证准确率作为网络精度的评估依据。

算法 1 PSO-CNN输入 运行次数(Nr),PSO群体粒子数(N),PSO最大迭代次数(itmax),训练数据(X,Y),个体极值与全局极值的选择阈值(Ctsh),网络层数范围(lmin,lmax),卷积层最大卷积核尺寸(kmax),全连接层最大神经元数(nmax),网络输出维度(dout),粒子评估前训练epoch数(etrain),最优框架测试前训练epoch数(etest)。 输出 最优CNN架构及其参数数量,测试准确率。1 for j=1 to Nr do2 S={P1,P2,…,PN}←粒子群初始化(Nr,N,lmin,lmax,kmax,nmax,dout)3 P1.pbest←P1,P1.grade,P1.pbest.grade←CNN粒子分数评估(P1,X,Y,etrain)4 gbest←P1,gbest.grade←P1.grade5 for i=2 to N do6 Pi.pbest←Pi,Pi.grade,Pi.pbest.grade←CNN粒子分数评估(Pi,X,Y,etrain)7 if Pi.grade≥gbest.grade then8 gbest←Pi9 end10 end11 for it=1 toitmaxdo12 for i=1 to N do13 Pi.velocity←CNN粒子速度计算(Pi,Ctsh)14 Pi←粒子更新(Pi,Pi.velocity)15 Pi.grade←CNN粒子分数评估(Pi,X,Y,etrain)16 if Pi.grade≥Pi.pbest.grade then17 Pi.pbest←Pi,Pi.pbest.grade←Pi.grade18 if Pi.pbest.grade≥gbest.grade then19 gbest←Pi,gbest.grade←Pi.grade20 end21 end22 end23 end24 CNN粒子分数评估(gbest,X,Y,etest)←gbest25 return gbest,gbest.nparamaters,gbest.grade26 end27 return gbest,average of gbest.nparameters,average of gbest.grade

3.2 粒子群初始化

粒子群初始化的过程即依据设定的网络层排列原则,随机生成粒子功能块组的过程,具体如算法2所示。排列原则的设定是为了保证架构的可行性和实用性,具体有以下几点:一是首层必为卷积层,尾层必为全连接层;二是全连接层不穿插于其他两层之间,即全连接层后只有全连接层,且本文将全连接层最大数量设置为5;三是需根据输入图像尺寸限定池化层数量,以避免深层特征图尺度过小而不能提取有效特征。添加网络层时,在设定的范围内随机生成该层的必要参数。添加卷积层时,生成卷积核尺寸大小及输出通道数;添加全连接层时,生成该层的神经元数量;添加池化层时,随机选择最大池化与平均池化,根据CNN的搭建经验,一般默认池化尺寸为3×3,步长为2×2。

3.3 粒子速度计算及更新

粒子群初始化完成后,保证群体向最优值靠拢的关键便是粒子速度的计算和粒子的更新。首先要解决的是粒子差异的计算,如算法3所示。

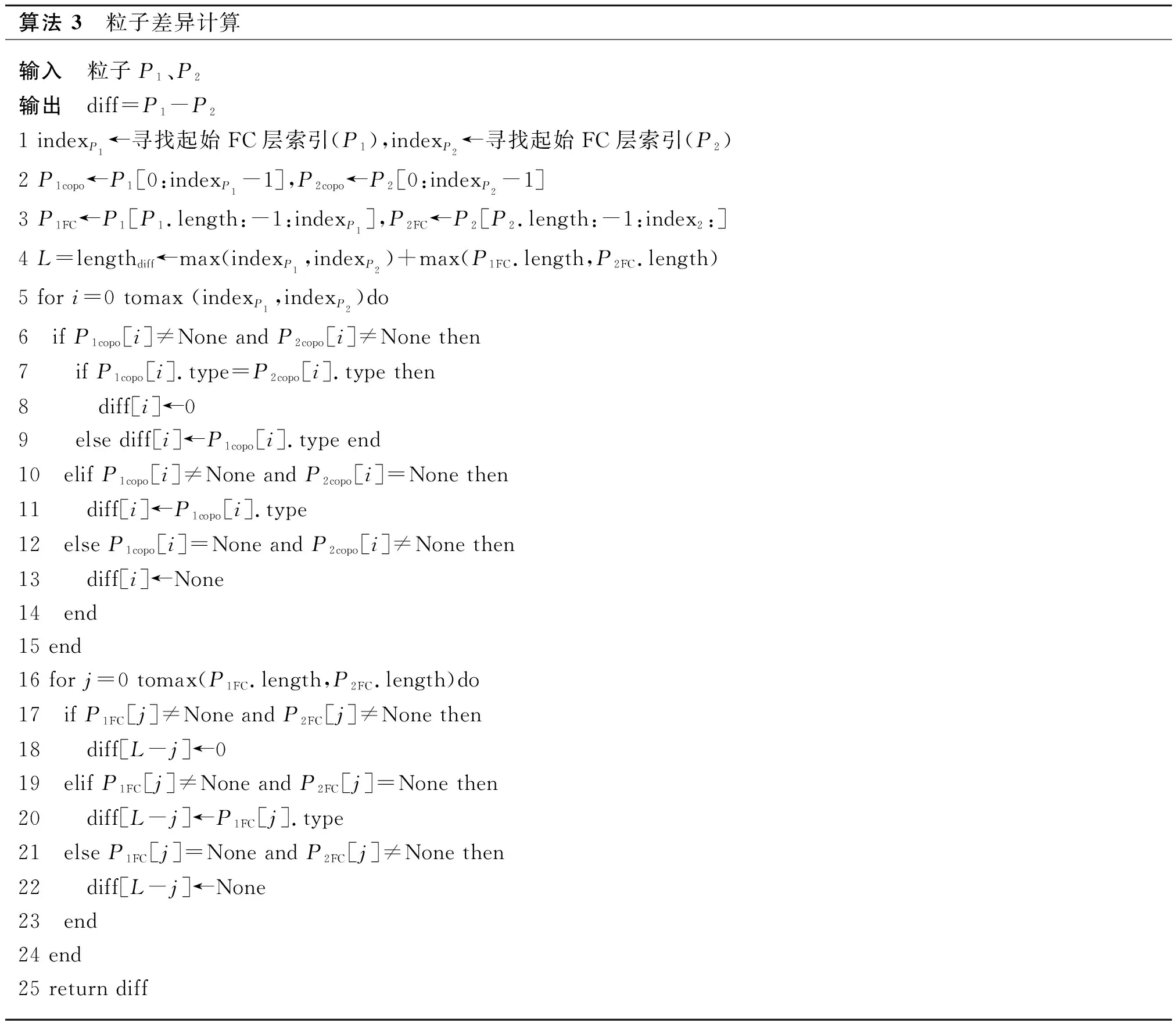
算法 3 粒子差异计算输入 粒子P1、P2输出 diff=P1-P2 1 indexP1←寻找起始FC层索引(P1),indexP2←寻找起始FC层索引(P2)2 P1copo←P1[0:indexP1-1],P2copo←P2[0:indexP2-1]3 P1FC←P1[P1.length:-1:indexP1],P2FC←P2[P2.length:-1:index2:]4 L=lengthdiff←max(indexP1,indexP2)+max(P1FC.length,P2FC.length) 5 for i=0 tomax (indexP1,indexP2)do6 if P1copo[i]≠None and P2copo[i]≠None then 7 if P1copo[i].type=P2copo[i].type then 8 diff[i]←09 else diff[i]←P1copo[i].type end10 elif P1copo[i]≠None and P2copo[i]=None then11 diff[i]←P1copo[i].type12 else P1copo[i]=None and P2copo[i]≠None then13 diff[i]←None14 end15 end16 for j=0 tomax(P1FC.length,P2FC.length)do17 if P1FC[j]≠None and P2FC[j]≠None then18 diff[L-j]←019 elif P1FC[j]≠None and P2FC[j]=None then20 diff[L-j]←P1FC[j].type21 else P1FC[j]=None and P2FC[j]≠None then22 diff[L-j]←None23 end24 end25 return diff

两个粒子计算差异时,为避免更新粒子时全连接层被放置于卷积层、池化层之间,故将粒子拆分为卷积池化(copo)与FC两部分,两部分相向分别计算差异值。差异值的计算以前粒子为主,若两粒子某位置层类型不同,diff选取前粒子类型;若两粒子某位置层类型相同,diff取为0。

粒子速度由各块随机选取(pbest-P)或(gbest-P)相应块构成,由于本算法中粒子的特殊性,抛弃原算法中的惯性部分。设定个体极值与全局极值的选择阈值(Ctsh),在每个位置随机生成一个(0,1)之间的数r。若r≤Ctsh,则选取(gbest-P)作为该位置的速度,反之则选取(pbest-P)。Ctsh控制着粒子趋近gbest的速度,Ctsh越大,粒子便越快趋近gbest,但同时粒子群的搜索范围变小,陷入局部最优的可能性变大。

根据式(3),新的粒子由粒子速度和原粒子相加构成。当粒子速度为0时,保留原粒子相应位置功能块;速度为N时,移除相应位置功能块;速度为C、P、F功能块时,则对原粒子功能块进行替换。整体算法示例如图2所示。

图2 粒子速度计算及结构更新示例Fig.2 Example of particle velocity computation and architecture update

需要指出的是,若在粒子更新后所含池化层数量超出依据输入图像尺寸计算的限额,则由后至前按序移除超额池化层。

3.4 基于PSO-CNN的波形识别算法的实际应用

本文所设想的算法实际应用框图如图3所示。天线侦收到射频信号,经过前端处理为中频信号,通过时频分析将中频信号转变为时频图像。随后制作训练集,标注出图像的波形类型,用于训练PSO-CNN模块,寻找出最优的CNN。最优CNN找出并训练完毕后,便可用其自动、快速、准确识别天线侦收的未知信号波形。在众多的时频分析算法中,WVD算法[15]具有最高的时频分辨率,但在处理LPI信号这种多分量信号时易产生交叉项干扰。SPWVD(smoothed pseudo Wigner-Ville distribution)[16]作为WVD的改进版本在保持高时频分辨率的基础上,很好地抑制了交叉项干扰。本文即采用SPWVD作为时频分析方法,SPWVD定义如下:

(6)

式中:s(t)为输入信号;t与f分别代表时间和频率;g(u)和h(τ)为两个汉明窗函数,且满足g(0)=(0)=1。

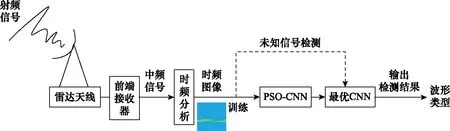
图3 算法实际应用框图Fig.3 Block diagram of algorithm’s practical application

4 仿真实验

4.1 建立LPI雷达信号数据集

本文所提出的LPI雷达波形识别算法针对7种最为常见的雷达信号,分别为线性调频(linear frequency modulation, LFM)、Barker码、Frank码及P1、P2、P3、P4码编码信号。信号生成具体参数选择如表1所示。其中,U(·)表示范围内均匀分布;U[·]表示范围内整数的均匀分布;{}表示可选参数集;fc表示载频;B表示带宽;N表示每信号周期采样数;LBc表示巴克码码长;Ncc表示每套编码包含的周期数;M表示频步;m表示子码长度;fs表示采样频率。在建立数据集时,大部分学者仅考虑加性高斯白噪声(additive white Gaussian noise,AWGN)的影响,这与实际信道相差很大。为更好地贴近真实环境,本文搭建莱斯衰落信道模拟信号传输过程,信道具体参数如表2所示。表2中AWGN大小使用信噪比(signal to noise ratio,SNR)来衡量。

表1 7种LPI雷达信号仿真参数

表2 莱斯衰落信道参数

信号生成完成后,使用SPWVD方法获取信号时频图像。同一信号由WVD与SPWVD获取的时频图像对比如图4所示。

图4 同一信号的WVD与SPWVD时频图像Fig.4 WVD and SPWVD time-frequency images of the same signal

相比较来看,和前面理论分析一致,SPWVD的效果远远好于WVD的效果。7种LPI雷达信号的SPWVD时频图像展示如图5所示。

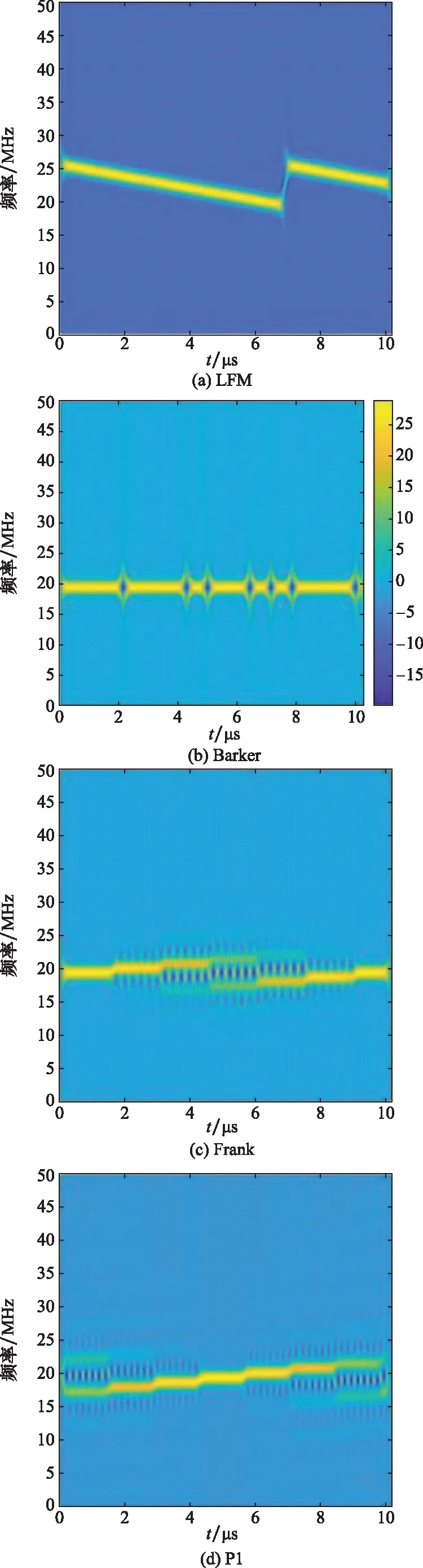
分析7种LPI雷达信号时频图像:LFM与Barker码编码特征区分度很高,其余5种信号虽较为相似,也具有可供区分的特征。Frank,P1及P2时频图像具有明显的阶梯状特征,而P3,P4信号则为边缘光滑的直线段;Frank及P3信号能量中心分布于图像左右两侧,而P1及P4能量中心聚集于图像中心;P2信号与P1图像特征极为相似,但两者时频图像中特征线段走势相反,P2为下行,P1为上行。总之,使用CNN对7种时频图像的识别分类具有可行性。数据集其他参数如表3所示。

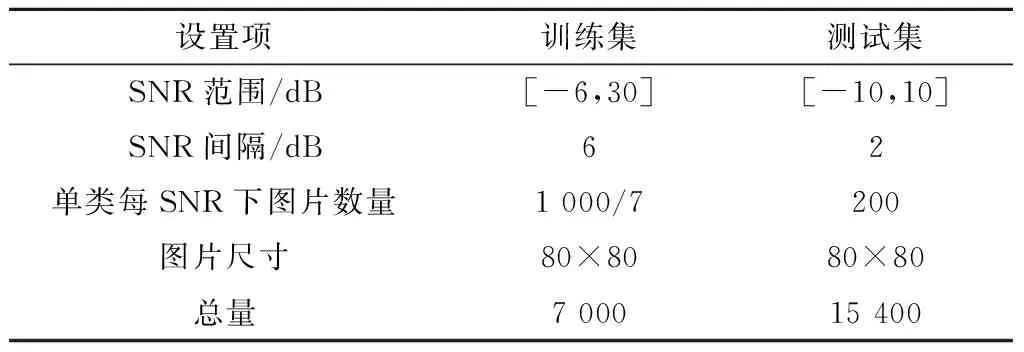
表3 数据集仿真条件设置

4.2 算法训练及评估

算法依托Tensorflow+Keras框架实现。作为一种高度模块化且具有用户友好应用程序接口的神经网络库,使用Keras搭建神经网络十分简单易行。本文实现的CNN粒子生成、更新,均是在以列表形式存在的功能块组上进行,Keras序列化模型可以较轻松实现对各功能块组的编译、训练及测试。

算法实验平台为Intel(R) Core(TM) i7-8565U CPU@1.80 GHz处理器,8 G内存,未使用显卡加速。

4.2.1 算法单精度指标训练及评估

为检验PSO-CNN算法寻找高识别精度CNN结构的能力,本节仅采取acc作为粒子的评估指标,即将式(5)中Cf设置为0。依据表4实施训练5次,得到每次训练的最优CNN粒子,训练结果如表5所示,其中acc-10为所选出的最优粒子进行10 epochs训练后的验证准确率。

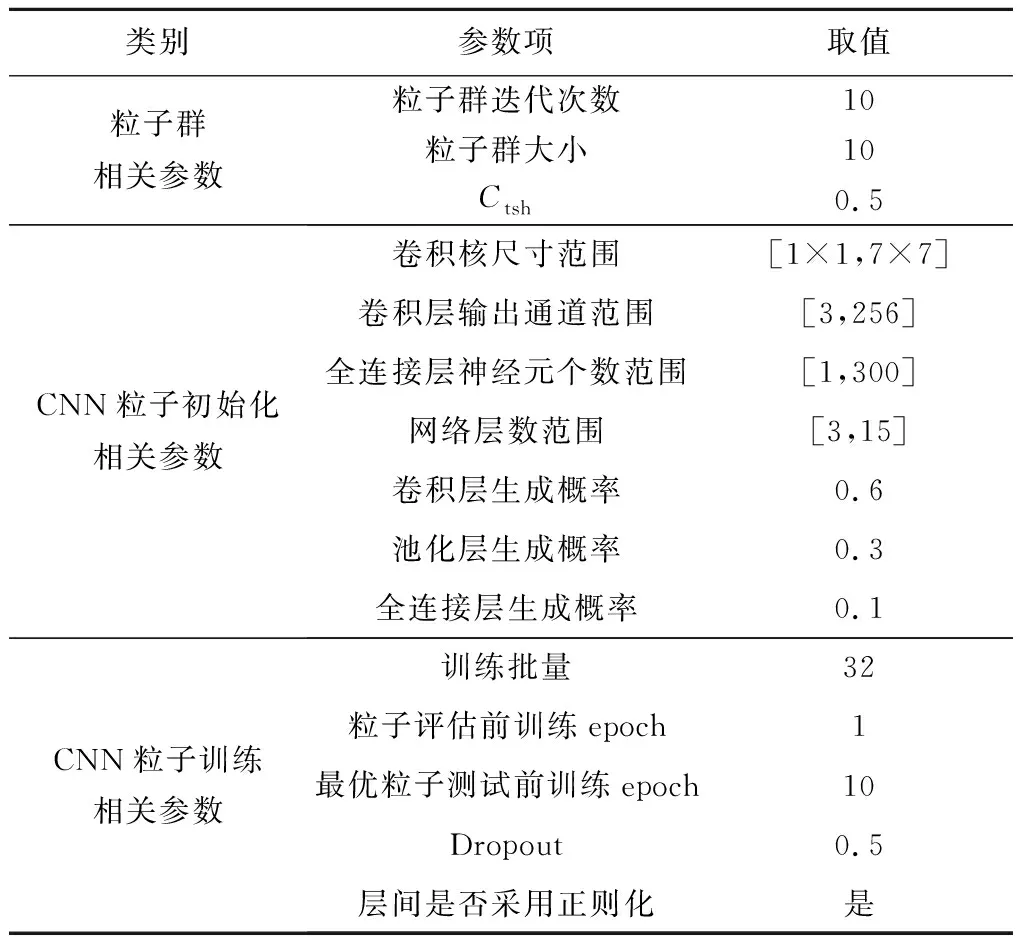
表4 PSO-CNN算法参数选择

观察表5,5次训练中的acc-10均超过97%,参数数量大多在百万级别。限于硬件水平,每次训练所花费的时间在10～27 h不等。

表5 单精度指标PSO-CNN算法训练结果

5次训练gbest进化曲线如图6所示。一次epoch训练后评估得到的gbest,在迭代中逐步更新。gbest的acc值呈递增趋势,经过10次迭代,acc值最终均达到80%左右的水平。

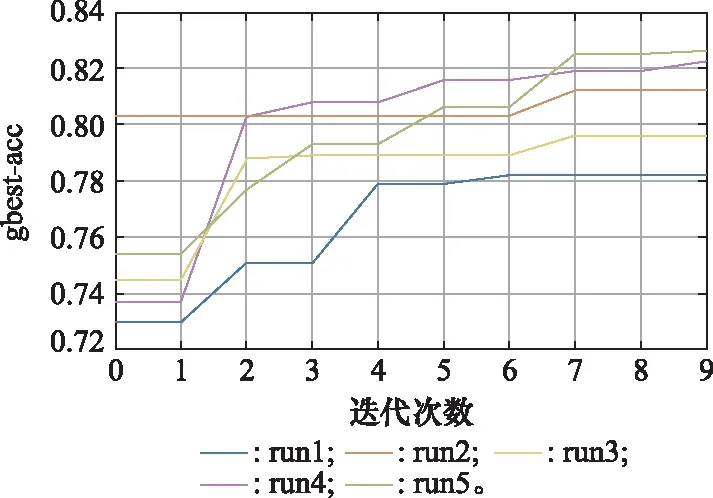
图6 单精度指标PSO-CNN算法训练gbest进化曲线Fig.6 Training gbest evolution curve of single precision index PSO-CNN algorithm

第3次与第5次所寻得的最优粒子精度最高,将这两次训练得到的最优CNN框架展示如图7所示。

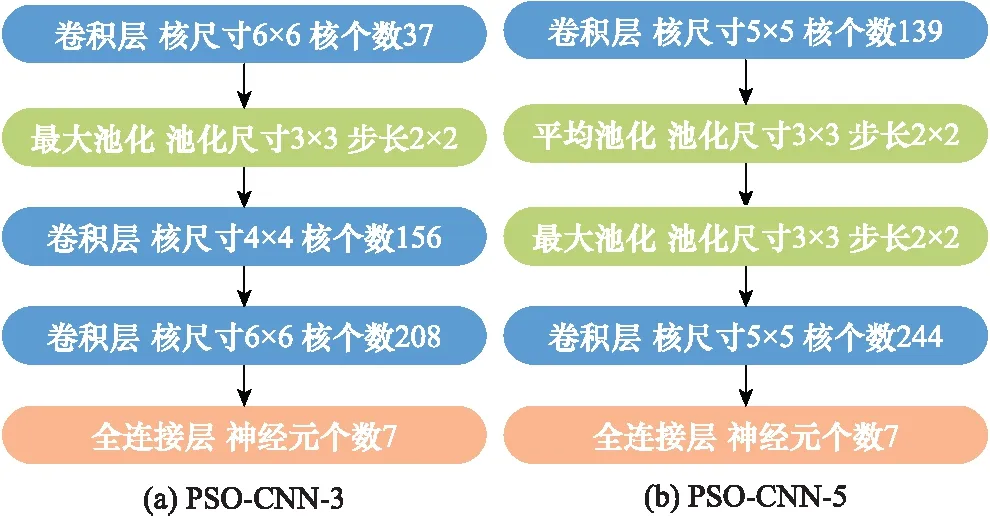
图7 单精度指标PSO-CNN算法获取的最优结构Fig.7 Optimal structure obtained by single precision index PSO-CNN algorithm

单精度指标PSO-CNN算法获取的CNN均为较浅的5层网络。由于数据集图像为简单的线条,所含的深层次特征较少,浅层网络更具有适配性。

选取LeNet[17]、ZFNet、AlexNet[18]、VGG13、VGG16、VGG19[19]、GoogleNet[20]、ResNet34及ResNet50[21]这9种经典CNN结构使用相同训练集进行训练,所得模型与PSO-CNN算法第3次、第5次训练所得模型在同一测试集上的检测效果如图8所示。

图8 与9种经典CNN的检测效果对比 Fig.8 Comparison of test results with nine classic CNNs

通过对比可以看出,单精度指标PSO-CNN算法获取的两种CNN结构在测试集上得测试效果超过了绝大部分所选取的经典CNN结构,直观展示了算法的优越性。11种CNN结构进一步的对比如表6所示,其中参数数量的计算以80×80的输入图像尺寸为准。

表6 与经典CNN的进一步对比

结合图7和表6可知,通过PSO-CNN算法寻优获取的两种CNN具有较简单的结构、最少的参数、快速的检测时间,同时实现了优越的检测精度。最少的参数保证了模型的轻量性,快速的检测时间保证了其实时性,在SNR≥0的情况下,PSO-CNN-3可实现94.8%的检测精度,也印证了模型的精确性。

限于硬件水平,11种CNN结构均在训练集上训练了10 epochs。与同为5层网络的LeNet相比,PSO-CNN算法所寻得的CNN结构表现出了更好的适用性。由于本实验使用的数据集特征相对简单,对于VGG16、ResNet-34等较深的CNN结构,一是提取过深层的特征易将简单问题复杂化;二是需要长时间充分训练,而这又易导致过拟合问题。

4.2.2 算法双指标训练及评估

在实际应用中,有时对模型轻量性要求很高而对模型精度的要求相对宽松,这就需要将模型复杂度也纳入粒子的评估指标,寻找更为轻量但同时满足一定精度要求的CNN结构。

在本节实验中,首先设定Cf=1,即双指标占比相同。将Nb依次设定为3.5×105、3.5×106及1.05×106,分别为单精度指标PSO-CNN算法寻优结构参数量级、一般经典CNN结构参数量级及取中参数量级。依据表4进行训练,为了解不同Nb对粒子迭代寻优的影响,训练过程中粒子pbest及gbest变化趋势对比如图9所示。

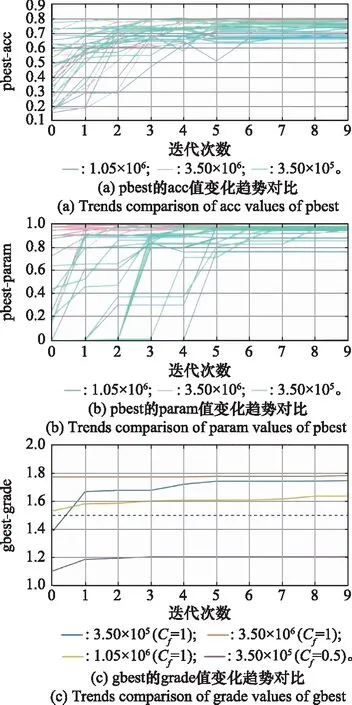
图9 不同Nb对粒子迭代寻优的影响Fig.9 Effect of different Nb on particle iterative optimization

如图9所示,采用双指标(1∶1)的PSO-CNN算法在迭代过程中可实现acc与param的同时寻优,粒子gbest的grade值也均为递增趋势。当Nb取3.5×106时取得最好的精度寻优效果,初始化粒子时param为非0值,说明初始化粒子的参数量均未超过3.5×106,随着迭代次数增加,param值很快逼近1值,一方面说明粒子优化有效,可同时也说明3.5×106量级相较于更新的粒子参数量过大,导致param值对粒子参数量变化的反应较小,粒子grade受param值的影响也相应较小。Nb取3.5×105时,在第3次迭代后param摆脱0值,全部粒子参数量降至3.5×105以下,这表明param值收敛较慢,粒子grade受param的影响较大,导致在更新粒子时较大的压缩参数量,生成的新粒子acc反而偶尔降低,出现了acc波动较大的情况。

基于不同Nb所选出的最优CNN网络结构的其他对比如表7所示。

表7 双指标PSO-CNN算法训练结果

表7结果显示,采用双指标(1∶1)的PSO-CNN算法寻优的CNN均为105量级,与单精度指标算法相比,大幅缩减了参数数量。Nb取3.5×105时实现了84.2%的检测精度,也满足了较高的精度要求。

在接下来的实验中,令Nb=3.5×105,Cf=0.5,依据表4进行训练以研究双指标(2∶1)的PSO-CNN算法的寻优效果。训练过程中粒子gbest变化趋势见图9(c)中的3.5×105-0.5Cf曲线,pbest变化趋势对比如图10所示。

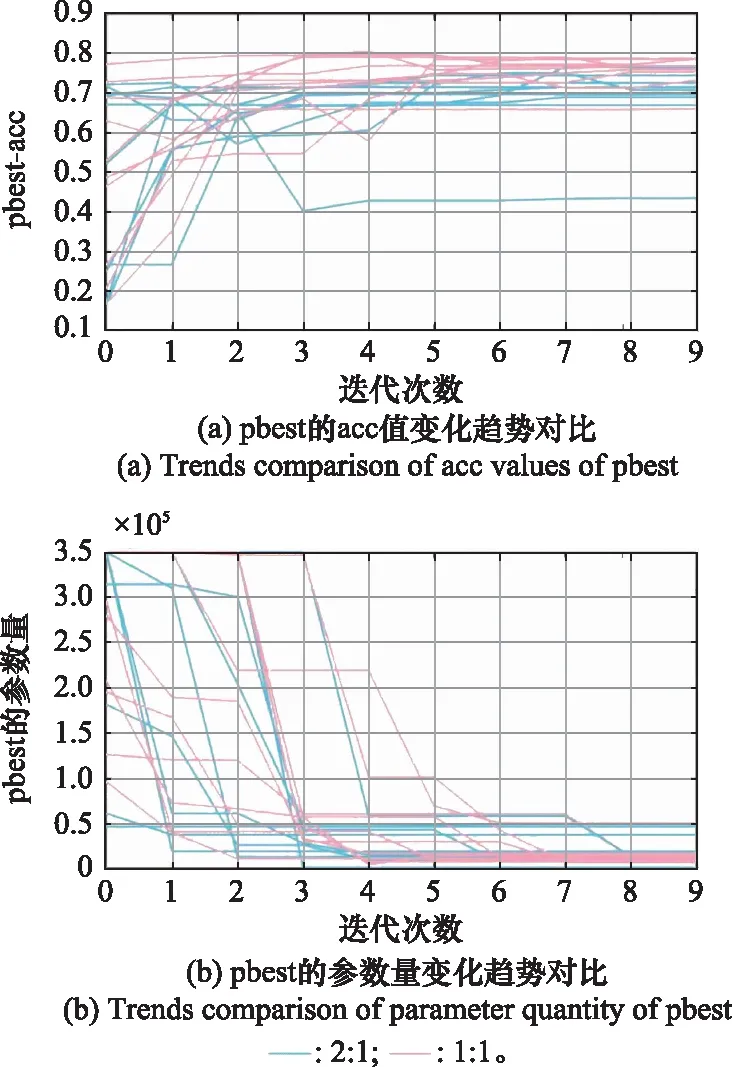
图10 不同Cf对粒子迭代寻优的影响Fig.10 Effect of different Cf on particle iteration optimization

图10结果表示,在Cf=0.5时,粒子群也可实现对grade的较快寻优,但与Cf=1时相比,粒子所能实现的acc略低且寻优网络的参数量也相对偏高。所寻得网络的其他对比如表7所示。总体对比,Cf=1时效果更好。

5 结 论

目前基于时频图像的LPI雷达波形识别多采用CNN作为特征提取和分类器,针对该领域CNN结构智能寻优这个难题,本文提出一种基于PSO-CNN的雷达波形识别算法。该算法基于识别精度及网络复杂度两种指标,使用PSO优化CNN,实现了较大范围内自动搭建层数不定、层类别及层内参数不定的CNN结构并进行迭代寻优。

仿真部分首先搭建莱斯衰落信道仿真更贴合真实环境的LPI雷达信号,之后使用SPWVD将信号转变为时频图像并建立数据集,使用PSO-CNN算法进行CNN结构的智能择优。算法评估结果表明,PSO-CNN算法获取的CNN结构与其余9种经典CNN结构相比,实现了对LPI雷达信号更好的检测效果,且更具轻量性、实时性、收敛性及适配性。由此可见,对LPI雷达信号波形的识别不能靠经典模型的套用,而是要挖掘适配该方向的专用CNN结构,本文研究成果可为其提供重要参考。

需指出的是,限于硬件水平,本文初始化的粒子群规模为10,这在一定程度上限制了算法寻优效果,导致训练结果出现波动的情况。在后续工作中,还将尝试把Inception块、残差块等纳入CNN智能寻优范围,以期获得更为精确高效的CNN结构,实现更好的LPI雷达波形识别效果。