基于梳状谱调制和间歇采样重复转发的复合干扰
2021-11-29周胜文沙明辉胡小春
周胜文, 沙明辉, 胡小春
(北京无线电测量研究所, 北京 100854)
0 引 言
近年来随着大规模数字集成电路在电子对抗领域的广泛应用,基于数字射频存储(digital radio frequency memory, DRFM)的干扰技术受到越来越多的关注[1-3]。间歇采样转发干扰基于DRFM技术采用收发分时工作体制,解决了收发同时工作体制下系统隔离度要求高的难题,同时干扰转发的延迟非常小,广泛应用于小型化干扰装备的实际工程研制中[4-5]。在间歇采样转发干扰的基础之上,文献[6]提出幅度均匀加权叠加的干扰样式,文献[7-8]研究了叠加干扰的时序优化和干扰效能;文献[9]分析了间歇采样重复转发干扰(interrupted sampling repetitive repeater jamming, ISRRJ)对脉内频率编码信号的干扰效果,文献[10]针对采用恒虚警处理的雷达提出优化ISRRJ参数的方法,文献[11]分析ISRRJ对线性调频信号的欺骗干扰和对相位编码的压制干扰。针对均匀间歇采样导致的假目标幅度递减问题,文献[12]提出间歇采样非均匀重复转发干扰(interrupted-sampling and nonuniform periodic repeater jamming, ISNPRJ),总结了干扰参数的选取步骤并对干扰效果进行分析,文献[13]提出间歇混沌采样的干扰方法,文献[14]针对相位编码雷达提出预测转发的干扰方法,相比直接转发和重复转发有更好效果。间歇采样在合成孔径雷达(synthetic aperture radar,SAR)和逆SAR(inverse SAR,ISAR)的干扰领域也有广泛应用,文献[15-21]研究了通过间歇采样干扰形成ISAR图像欺骗的方法,文献[22-24]则将间歇采样干扰的思想应用于SAR欺骗干扰。结合不同干扰样式的优点开展复合干扰样式的研究是另一个重要的研究方向,文献[25]提出基于灵巧噪声卷积调制和ISRRJ的复合干扰方法,文献[26]提出基于频移干扰和ISNPRJ的复合干扰方法,复合干扰相比单一干扰样式具有更高干扰效能。
梳状谱调制干扰(comb spectrum modulation jamming, CSMJ) 本质上是一种多分量的频移干扰,被广泛用于欺骗干扰[27]和压制干扰[28],但是当梳状谱的数量较少时,CSMJ形成的稀疏假目标容易被雷达采用各种抗干扰技术识别出来并被剔除掉[29-35]。本文提出基于CSMJ和ISRRJ的复合干扰方法,通过梳状谱调制参数控制假目标的分布范围,利用间歇采样重复转发特性使假目标的个数倍增。新方法通过调节复合干扰参数控制字,能够产生幅度均匀分布的密集假目标群,具有良好的欺骗兼压制干扰效果。
1 CSMJ
设雷达发射时宽为T,带宽为B的线性调频(linear frequency modulation, LFM)脉冲信号,其信号形式如下:
(1)
式中:f0为载频;rect (·)为矩形函数;μ为调频斜率且μ=B/T。
梳状谱信号是M+1个单频连续波的加权和,其信号形式如下:
(2)
式中:am为第m+1个信号的幅度;fm为第m+1个信号的频率。
CSMJ制干扰是将截获的雷达信号x(t)与梳状谱信号进行时域乘积调制从而产生相参欺骗干扰,梳状谱干扰Jcomb(t)为
(3)
雷达脉冲压缩匹配滤波器的单位冲击响应为h(t)=x*(-t),则干扰信号经过匹配滤波器后输出为
(4)
式中:*为卷积运算;F(t,am,fm)为干扰输出的第m个分量,其信号形式为
(5)
式中:sinc(x)=sin(πx)/πx为辛克函数。
由式(5)可知,CSMJ经LFM雷达脉冲压缩处理后其输出为多个单频震荡,其包络为M+1个sinc 函数的加权和。当fm>0时, 第m个分量的脉压峰值将在真实目标回波脉压峰值之前出现,形成前置性干扰效果。当雷达信号调频斜率一定时,CSMJ信号经脉冲压缩处理后形成的多个假目标峰值点位置与梳状谱各个频率点的频率值成正比,假目标间隔与梳状谱相邻谱线频率差成正比。通过设置梳状谱频率数量和频率值,可产生不同分布的假目标。
CSMJ在脉冲压缩处理后形成的假目标时间间隔为(fm+1-fm)/μ,换算为距离间隔为ΔR(fm+1-fm)T,ΔR为LFM脉冲压缩雷达的距离分辨率,即ΔR=c/2B,c为光速。当假目标间隔小于雷达距离分辨率时,即(fm+1-fm)T≤1,则梳状谱干扰为密集假目标压制干扰。
若假目标保持相同间隔,间隔为若干个雷达分辨单元且假目标均分布在真实目标之前,则
fm=mΔf
(6)
式中:Δf=L/T为频率间隔,L为假目标间距控制字。由|fm| (7) 间歇采样干扰是指接收到雷达信号后只采样较短的时间就进行处理转发,然后再继续采样后续脉冲并处理转发,采样和转发的过程分时交替进行。 间歇采样脉冲p(t)是一个脉宽为τ,重复周期为Ts的矩形包络脉冲串,可表示为 (8) 式中:δ为单位冲激函数,对采样脉冲p(t)进行傅里叶级数展开可得 (9) 式中:fs=1/Ts;b0=τfs;bn=τfssinc(nfsτ)。对截获雷达信号进行采样处理,即与间歇采样信号相乘,则间歇采样转发干扰信号为 (10) 如果真实目标的回波通过匹配滤波器的响应为y(t)=x(t)*h(t),由式(5)可知干扰信号经过匹配滤波器的输出为 (11) 间歇干扰信号所产生的假目标包含两部分:零阶假目标和高阶假目标,高阶假目标幅度逐渐减少且对称分布在零阶假目标两侧[4-5],根据线性调频信号的时频耦合关系,脉冲压缩后假目标的距离间隔为fsTΔR。 当采样一次重复转发K次时,干扰信号为 (12) 其匹配滤波输出为 (13) 间歇采样重复转发K次时各假目标幅度bn=sinc(n/(K+1)/(K+1)。如果假目标回波功率大于真实目标功率判定为有效假目标,则K次重复转发干扰的假目标总数为 (14) 其中xn为 (15) 式中:JSR为干信比,表示干扰信号功率和目标回波的功率比值。不同重复转发次数的条件下假目标个数与JSR的关系如图1所示,由图1可知,假目标个数受到干信比的制约,不能单纯靠增大重复转发次数来增加假目标个数,实际应用中应结合干扰功率选择合适的重复转发次数。 图1 不同转发次数下JSR和假目标数量关系Fig.1 Relationship between JSR and false targets amount with different repetitive times 由第1节可知,梳状谱干扰能够形成数量、幅度、间隔可控的多假目标,但是假目标数量与间隔控制字的乘积受到脉冲压缩增益的约束;由第2节可知,间歇采样干扰形成的假目标群的幅度随着距离散布的扩大按照sinc函数递减,并且随着重复转发次数K的增加进一步降低。 因此,将梳状谱调制和间歇采样重复转发结合起来形成新的复合干扰样式,可以充分利用不同样式的优点,为产生幅度分布均匀的密集假目标群提供一种可能。 设复合干扰信号为J(t),其信号形式为 (16) 根据式(5)和式(13),干扰信号经过脉冲压缩处理后表示为 (17) 由式(17)可知,复合干扰方法可形成K组假目标群,各假目标群之间的间距为BτΔR。每组假目标群又包括两个部分,第1部分以梳状谱干扰为主假目标群,假目标的数量和间隔可通过梳状谱函数的控制参数进行调节,假目标幅度较大,假目标个数较少;第2部分为分布在主假目标左右两侧的次假目标群,该部分假目标的幅度随着远离主假目标减小,假目标个数较多。 当梳状谱形成的假目标群的总距离大于重复转发形成的假目标间距时,即 Bτ≤ML≤BT (18) 复合干扰可形成掩护区间较宽的密集假目标,反之,转发的假目标群之间出现较大缝隙,不利于掩护真实目标。 当梳状谱调制形成的假目标间距大于间歇采样假目标的间距时,LΔR>fsTΔR,即 L(K+1)τ≥T (19) 间歇采样形成的次假目标群可以分布在梳状谱调制形成的距离区间,此时干扰能量集中。 根据雷达信号时宽、带宽、间歇采样脉宽和干信比选取复合干扰的控制参数M、L、K的步骤如下: (1) 重复转发次数一般选择1~4,JSR较大时可选择较大K值; (2) 受干扰响应时间的限制同时考虑工程应用中开关切换时间,间歇采样脉宽τ一般选择为若干微秒; (3) 根据式(19)选择梳状谱间距控制字L; (4) 根据式(18)选择梳状谱个数控制字M。 当干扰控制参数满足上述条件时,新的复合干扰方法能够形成一定距离区间上幅度均匀分布的密集假目标群。 针对新的复合干扰方法的控制参数选取问题,设计仿真实验进行对比分析,用于证明理论分析的正确性。 仿真参数设置如下:雷达信号脉冲宽度T=10 μs,带宽B=10 MHz;CSMJ干信比JSR=20 dB。仿真结果如图2所示。 图2 不同参数条件下CSMJ干扰效果对比图Fig.2 Contrast diagram of jamming effect using CSMJ with different parameters 从图2可以看出,梳状谱调制干扰形成的假目标个数分别为11、4、5、5,假目标间隔分别为60 m、150 m、300 m、300 m;假目标个数和间隔与理论相符。对比图2(a)和图2(b)可知,假目标个数越多,干扰输出幅度越小。对比图2(b)和图2(d)可知,M、L越大,假目标覆盖范围越宽,假目标幅度的衰减也增大,需要利用式(7)进行幅度校正。 仿真参数设置如下:雷达信号脉冲宽度T=100 μs,带宽B=50 MHz; ISRRJ干信比JSR=20 dB。仿真结果如图3所示。 对比图3(a)和图3(b)、图3(c)和图3(d)可以看出,相同参数条件下增大重复转发次数K可以增加假目标个数,但是假目标干扰能量降低。对比图3(a)和图3(c)~图3(d)可以看出,相同参数条件下,增加间歇采样宽度,假目标间隔减少,假目标越密集。 4.3.1 不同重复转发次数仿真分析 仿真参数设置如下:雷达信号脉冲宽度T=100 μs,带宽B=50 MHz;复合干扰干信比JSR=20 dB,采样脉宽τ=2 μs。仿真结果如图4所示。 对比图4(a)和图4(b)可以看出,在其他参数相同的条件下,增加转发次数可以扩大假目标距离覆盖区间,但是假目标幅度减小;对比图4(b)和图4(d)可知,增大梳状谱间隔,可以改善间歇采样造成的能量分散;当ML 4.3.2 不同采样脉宽仿真分析 仿真参数设置如下:雷达信号脉冲宽度T=100 μs,带宽B=50 MHz;复合干扰,干信比JSR=20 dB,重复转发次数K=3。仿真结果如图5所示。对比图5(a)和图5(b)可以看出,采样脉冲宽度增加可以扩大假目标距离覆盖区间,但是假目标覆盖空隙变大,总的有效覆盖范围不变;对比图5(b)和图5(d)可知,增大梳状谱间隔,虽然干扰幅度降低,但是有效覆盖范围增加。 本文提出一种基于CSMJ和ISRRJ的复合干扰方法,通过对CSMJ的仿真分析,推导出幅度校正公式以及假目标个数与间隔控制字的约束关系;通过对ISRRJ的仿真分析,给出假目标个数、干信比、重复转发次数的关系。针对复合干扰形成的密集假目标的特性,给出复合干扰参数控制字的选择步骤,并进行干扰效果仿真分析。理论分析和仿真结果表明,新方法不仅能够形成幅度均匀分布的密集假目标群,而且参数控制简便,下一步将开展具体工程应用工作。2 ISRRJ


3 复合干扰
4 仿真分析
4.1 CSMJ仿真分析
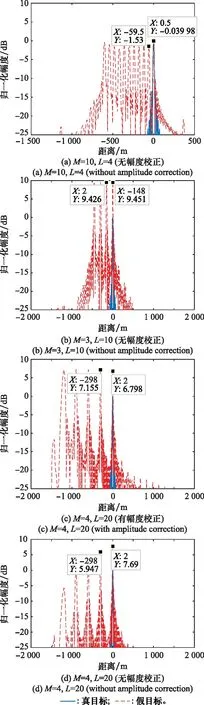
4.2 ISRRJ仿真分析
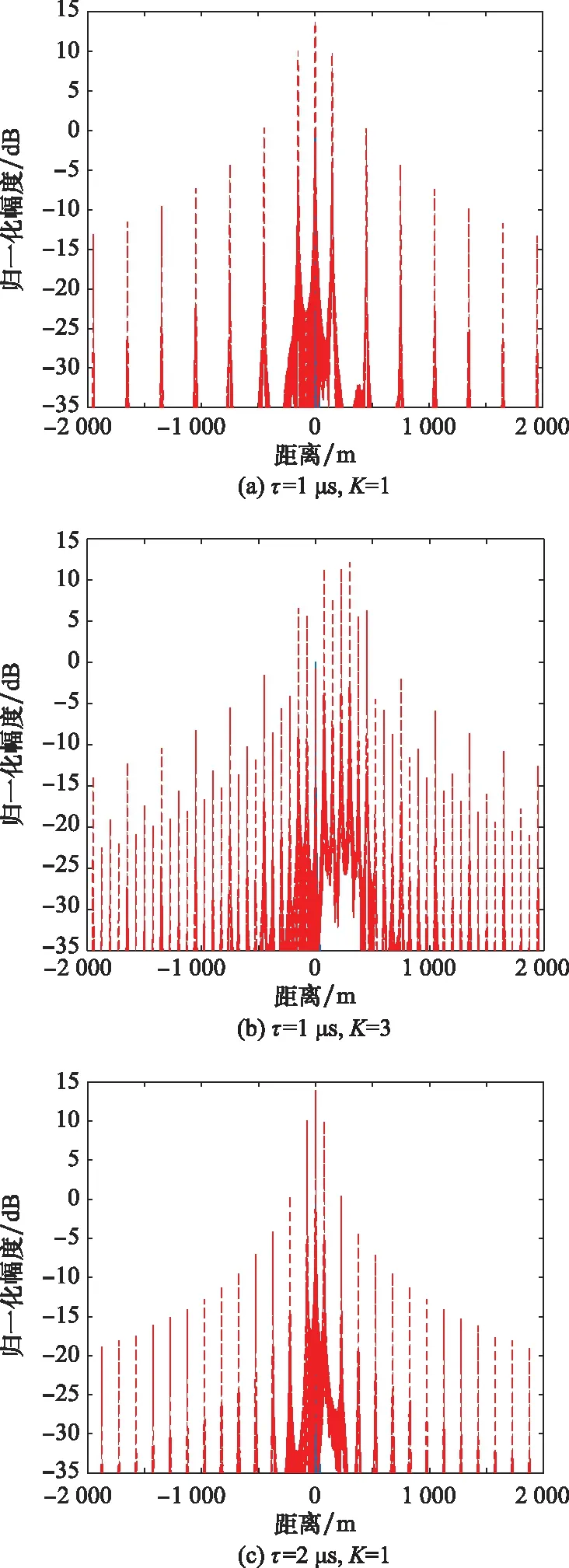
4.3 复合干扰仿真分析
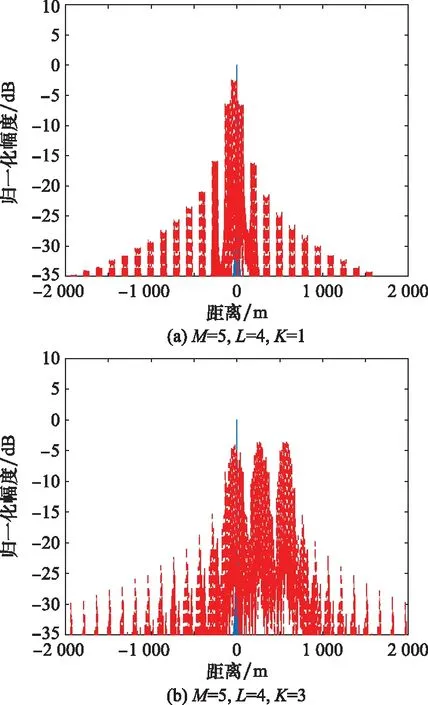
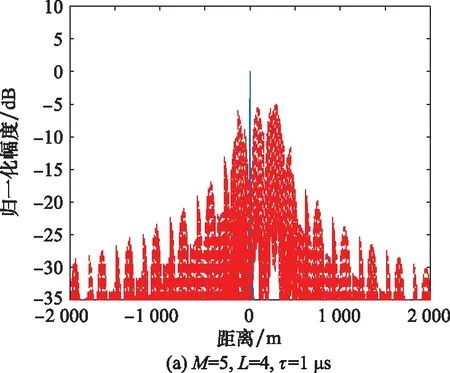
5 结 论
