阿仑纽斯公式在核电厂电仪设备时限老化分析中的研究与应用

刘 华，游 洲，刘亚男，刘飞洋，王 伟，黄国玉，欧阳宏志，邱 蕾，王新林

（1.南华大学 电气工程学院，湖南 衡阳 421001；2.中国核动力研究设计院 核反应堆系统设计技术国家级重点实验室，成都 610041）

为保证核电厂的运行安全，必须对1E级电仪设备进行环境鉴定。由于核级设备的可靠性将直接影响核电站的安全运行，因而核级数字化仪控系统在自主化过程中应按照相关法规和标准进行设备鉴定[1]。同理，为了保证核电厂延寿期间的运行安全，必须对1E级仪表进行基于时限老化分析的环境鉴定。时限老化分析涉及热老化分析、湿热循环分析、运行延寿期间的累积辐照分析、抗机械振动分析和地震试验分析等。其中，热老化分析通常使用阿伦纽斯公式及其模型进行评估。

1 阿伦纽斯公式和模型

1.1 热老化模型方法

模拟实验需要解答一个问题，即老化分析对象或产品在可控的实验环境中，测试一段时间相当于产品在实际使用条件下使用多长时间[2]。热老化模型的意义不仅在于可以极大地降低实验成本，也让测试更具目的性和针对性，有利于测试人员对整体时间的掌控。热老化通常使用阿伦纽斯模型进行评估，Nelson在文献中描述了该模型[3]。

环境试验是用以考核设备在寿期内存储，以及正常环境条件、异常环境条件下的耐受能力[4]。从环境试验的角度，阿伦纽斯模型为老化建立了一个基于材料、温度的函数，可在给定温度下估算热老化寿命，还能将分析对象给定温度下的剩余寿命与另一温度下的剩余寿命联系起来。

式（2）中，t为达到指定的使用寿命结束条件或生命周期的时间；B为常数。

可以使用阿伦纽斯模型进行等效老化，从而在给定不同的试验温度T1和试验周期t1的情况下，计算实际(或预期)安装和使用的环境温度T2下的寿命t2，见式（3）：

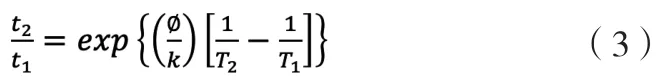
在某些情况下，设备本身的操作会导致环境温度的局部升高。电磁阀等设备在通电时自热就是这种情况，运行期间引起局部热上升，使设备所处的实际温度明显高于环境室温。式（4）在确定设备整体使用寿命时，考虑了间歇运行期间自热的影响。

式（4）中，T1为鉴定测试温度；t1为鉴定测试时间；T2e为通电时的最高预期温度；t2为计算的使用寿命；T2ne为断电时的最高预期温度；PHR为预计设备通电的最大时间百分比。

1.2 阿伦纽斯热老化模型的前提条件、敏感性和局限性

一般而言，关于美国核电厂执照更新申请与审查，估算整个过程需花费大量人力物力，大约4～5年时间。因此，美国核管会将提出执照更新申请的时间进一步限定在运行执照到期前至少5 年。该流程里的步骤“分析与评估”、步骤4“核管会审查与批准”2这两个环节是整个过程的核心，前者的责任方是执照更新申请者，如核电厂业主和/或营运单位，后者的责任方为执照更新申请的审查者，即美国核管会。

阿伦纽斯方法论广泛地用于热老化效应的量化计算。阿伦纽斯热老化模型有前提条件、敏感性和局限性三方面影响因素。在应用该方法评估热老化效应时，了解其潜在的局限性是至关重要的。下面具体分析总结这些前提条件、敏感性和局限性，以帮助理解阿伦纽斯方法的有效应用，并在适当应用时保守地论证该模型[3]。

点评：本研究的特色之处在于，应用网络建模分析的方法，揭示了转录调节因子基因靶向的性别特异性模式与结肠癌的存活结果相关。这种方法也可用于了解性别如何影响其他癌症的进展和对治疗的反应。

单一的应激源类型，如热老化，是假定贯穿于材料的整个生命周期。假设一个主要的化学反应对应于一个主要的老化机制，应选择合适的测试温度，以确保在测试条件下的主导老化反应，在安装使用条件温度下，也是主导和等效的。

根据气体反应理论，比例系数“A”大约以温度的平方根增加。当所有的反应物都不是气态时，这种温度依赖关系就会改变。这种假设可能会使计算值产生少量误差——对于典型的环境温度和测试温度，误差小于5%。基于以上原因，这个小误差将被其他保守的假设所弥补。因此，假设式（1）中的比例系数“A”与温度无关。

活化能随温度和时间的变化是恒定的，上述方程对所选活化能的精度非常敏感。由于活化能通常只有1～2个有效位，因而应谨慎选择活化能，并对其表达结果进行合理解释。

假设反应速率不受反应物浓度损耗的影响，换句话说，在耗尽效应（退化量）明显之前结束使用。这个假设是保守的，因为反应物的消耗降低了老化反应的速率，这将在相同降解量的基础上给出一个寿命端点，从而给出一个更长的预期寿命。

式（3）假设从一组温度条件下的时间转换为另一组温度条件时，退化损伤量相同。

由于前面所述的限制和前提条件，尽管阿伦纽斯热老化模型已被监管机构普遍接受，但它只能提供设备预期使用寿命的估计。在可行的情况下，应考虑结合状态监测或其他方法来共同验证设备的剩余寿命。

2 阿伦纽斯公式的应用

阿伦纽斯模型常常与时间、温度和热老化有关。该模型可用于估算给定温度下的热寿命，将某一温度下的剩余寿命与另一温度下的剩余寿命联系起来。下面为基于阿伦纽斯方程的应用案例。

2.1 使用寿命的测定

应用场景：已知发射器在203°F（368 K）加速条件下热老化2584h，发射体中的敏感材料活化能为0.78 eV。如果安装在环境温度为116°F（320K）的位置，该发射器的预期使用寿命是多少。

将相关数据代入式（3），进行计算和整理：

2.2 计算物质的活化能

应用场景：已知阿伦纽斯模型，分析对象在333 K和423 K的失效时间分别为350400 h和350 h。这种物质的活化能是多少。

2.3 自加热调整

应用场景：电磁阀在325°F的加速条件下热老化288h。阀门内的极限老化敏感材料是一种活化能为0.94 eV的弹性体。当阀门通电时，自加热升温到11.2°F。该阀门预计有10%的通电时间，其安装在环境温度为104°F的地方的发射器的预期使用寿命是多少。

将相关数据代入式（4），进行整理和计算：

式中，T1：鉴定测试温度为325°F，即435.93 K；t1：鉴定测试持续时间为288 h；T2e：通电时的最高预期温度为115.2°F，即319.37 K；T2ne：断电时的最高预期温度为104°F，即313.15 K；PHR：预计设备通电的最大时间百分比为0.1。

2.4 环境变化下的加权平均温度

应用场景：在装置的使用寿命内，预计已安装的装置将暴露于下面条件：20℃（293.15 K）环境15年；40℃（313.15 K）环境14年；60℃（333.15 K）环境11年。已知=1eV，计算整个使用寿命的阿伦纽斯加权平均温度Tn是多少。

将相关数据代入式（5），再进行整理和计算：

3 经验法则10℃定律的分析

3.1 经验法则10℃定律

由于有限部件缺乏活化能数据的情况下，“10℃定律”严格来说，是一种经验法则[6]，用来粗略地近似于与温度有关的反应。根据这条经验法则，使用温度每上升10℃（K），特定温度的反应速度就会增加一倍（或寿命减少一半）。RCC标准体系中规定试验的基准值是温度为135℃，时间950 h（设备预期寿命40年）。这些数值可用“10℃定律”调整，即：试验温度每增加（或降低）10℃，相应试验期限降低一半（或延长一倍）。

式（6）中，tSER为与使用温度对应的实际寿命；tage为老化时间；tage为老化温度，单位：℃或K；tSER为使用温度，单位：℃或K。

3.2 10℃定律的应用举例

场景描述：某一特定设备在50℃下的使用寿命为5年，但与极限构件材料相关的活化能尚不清楚。估算85°F（29.44℃）的近似预期寿命。

将相关数据代入式（7）：

通过增加环境的严酷性进行加速热老化试验。该试验的严酷程度由试验温度和持续时间来表示，数值的组合与设备预期寿命相关。由于“10℃定律”没有理论基础，一般情况下TLAA分析不建议使用。

4 小结

在众多的环境因素中，温度对产品的性能参数影响最大也最为常见，同时也是使用频率最高的环境因子。分析阿伦纽斯热老化模型的前提条件、敏感性和局限性，对其可能的局限性以及修正方案给出了说明。依托阿伦纽斯公式进行等效老化，可以作为工程上加速老化的理论基础，对诸多场景进行了案例分析和计算。通过研究将阿伦纽斯公式应用在核电厂电仪设备时限老化分析中的热老化分析，论证了阿伦纽斯公式比“10℃经验法则”更科学。