基于时间序列分解的降雨数据挖掘与预测

赵然杭，甘 甜，逄晓腾，王兴菊，苟伟娜，齐 真

（1.山东大学土建与水利学院，济南250100；2.青岛市供水事业发展中心，山东青岛266071）

0 引 言

降雨是水文过程的重要环节，能直接反映区域气候变化及水文过程，降雨量变化直接关乎区域水资源开发利用乃至影响社会经济发展。近年来，由于气候变化与人类活动的影响，生态问题严峻、洪旱灾害频发，充分挖掘降雨时间序列所含信息能更好揭示其自然规律，为水资源的规划管理提供科学的指导，促进人与自然和谐共处。对降雨量数据准确预测能为防洪抗旱工作提供科学的建议，进而改善居民生活质量，促进区域政治与经济的发展，是事关民生的大事。

数据挖掘是指从大量的、有噪声的、模糊的、随机的数据中，提取隐含其中的有用的信息和知识的过程［1］。国内外学者对降雨时间序列数据挖掘进行了相关研究：李宜轩运用线性拟合的方法，综合分析了桓台县1981-2018年的降水趋势变化情况，结论与实际情况相符［2］；衡彤等采用小波变换方法，对新安江流域黄山地区降水量时间序列的多时间尺度变化及突变特征进行了探讨，研究分析了主汛期降水与年降水的主周期，两者较为接近，结果合理［3］；李平兰等分析了1970-2015年会东县的降水变化特征，采用了累积距平法与Mann-Kendall 法的突变点综合判定方法，弥补了单个方法检验能力的不足［4］；Moravej等基于线性时间序列模型，利用ADF 函数、Mann-Kendall 检验，对伊朗West Azerbaijan 省的降雨时间序列进行了趋势分析，模型结论准确且适用性较强［5］。

国内外学者对降雨时间序列数据预测进行了相关研究：王晓鹏等应用基于Box-Jenkins方法的时间序列分析技术，针对青南高原的四个典型地区1961-2005年降水量序列，建立了自回归滑动平均模型对未来降水量进行了预测，模型因能反复识别修改，适用于复杂情况的数据拟合与预测［6］；贾海峰等提出了灰色-时序组合预测模型，能对年降雨量进行中长期预测，并以北京市大兴县黄村气象站35年降雨量资料为例进行了验证，模型能满足精度要求，且对其他既具有摆动又有趋势数据的模拟和预测同样适用［7］；高瑞华利用烟台地区1981-2010年降水资料，建立了干旱的灰色预测GM（1，1）模型，对2010-2030年的干旱灾害进行了预测，模型通过了残差与后验差检验分析，在短期预测时精度能满足要求，但不适用于长期预测［8］；Kolachian 等采用分位数映射与平均贝叶斯模型，通过提高观测值与集合预报平均值之间的相关系数，对欧洲中心2020年各月份不同降水模式的若干气象站的观测降水序列进行了预报，结果较为准确［9］。

以上研究分别对降雨时间序列进行了数据挖掘或预测，没有将数据挖掘与预测建立紧密联系，而数据挖掘能为数据预测提供信息支撑，数据预测结果也能验证挖掘的准确性，两者相辅相成。由于降雨时间序列受趋势、周期与突变等因素影响，复杂多变，需要在充分挖掘数据信息的基础上，进行降雨时间序列的预测研究。因此开展基于时间序列分解的降雨数据挖掘与预测研究，为雨（洪）水资源管理工作提供决策技术支持。

1 研究理论与方法

1.1 时间序列法简介

降雨时间序列因受多种因素影响，存在着趋势性、周期性、突变性等多种变化特征，将时间序列分解为趋势项、周期项、突变项与随机项并对各项进行分析与研究能更好揭示降雨量数据的变化规律。设X为时间序列，T为趋势项、P为周期项、B为突变项、R为随机项，则X可以表示为：

常见的趋势项分析法包括：累积距平［10］、Mann-Kendall 趋势分析［11］、Hurst 指数［12］、特征点［13］，周期项分析法包括：小波分析［14］，突变项分析法包括：Mann-Kendall 突变检验［15］、Pettitt 突变检验［16］，随机项检验法包括：自相关图和单位根［17，18］。

1.2 基于时间序列分解的降雨数据挖掘-预测模型

提出了基于时间序列分解的降雨数据挖掘-预测模型（Data Mining And Forecasting model，DMAF 模型），不仅能挖掘出降雨时间序列的内在信息，还能对其进行准确预测。

（1）数据挖掘方面：①数据分解：对于降雨时间序列X，采用特征点法分解其趋势项T；小波分析法分解其周期项P；Mann-Kendall法、Pettitt法进行突变性分析，无特殊情况突变项B不予考虑；计算余项X-T-P-B得随机项R。②数据挖掘：分别采用累积据平法、Mann-Kendall趋势分析法、Hurst指数法、特征点法进行趋势分析，采用小波分析法进行周期分析，采用Mann-Kendall 法、Pettitt 法进行突变性分析，采用自相关图法、单位根法对随机项进行检验。

（2）数据预测方面：利用线性延长方法将趋势项T基于特征点法的末端直线进行延长得到Ty，利用Matlab 小波工具箱Extend 函数将周期项P进行延长得到Py，无特殊情况下不考虑突变项，采用NAR 神经网络法对随机项进行预测。然后，将延长后的趋势项Ty、周期项Py与预测所得随机项Ry相加得预测结果，流程如图1 所示。为提高预测精度，将NAR 神经网络经遗传算法进行优化，其流程图如图2。

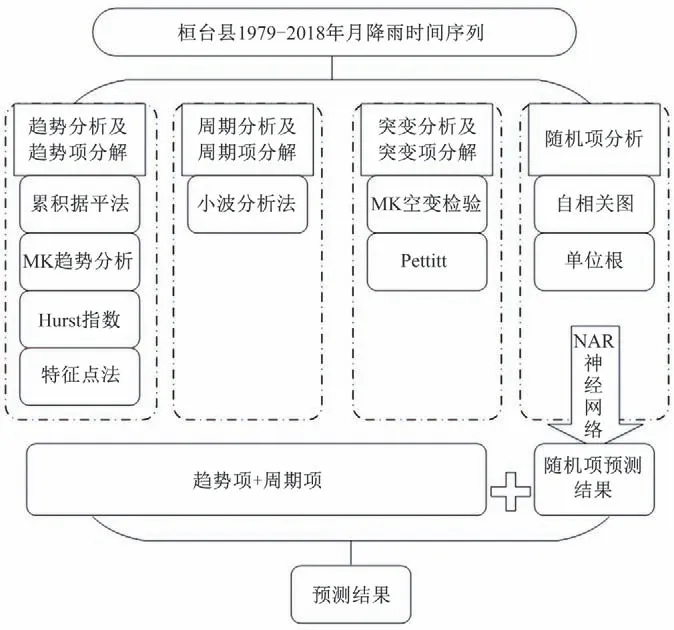
图1 研究流程图Fig.1 Research flow chart

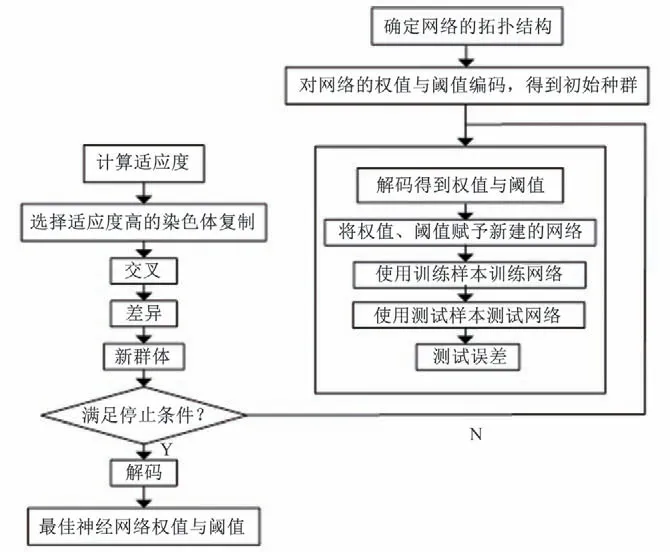
图2 基于遗传算法的神经网络优化流程图Fig.2 Neural network optimization flow chart based on genetic algorithm

2 基于时间序列分解的降雨数据挖掘-预测应用实例

2.1 研究区域概况与数据来源

桓台县是淄博市下辖县，位处鲁中山区和鲁北平原的结合地带，人口50.15 万，县域面积498.25 km2，属暖温带季风气候［19］。桓台县河网较为密布，乌河、东西猪龙河、孝妇河、涝滞河、小清河、预备河等10余条河流流经县内，但因处于鲁山北麓山前洪冲积平原和黄泛平原迭交地带，南受鲁中山区洪水冲积，北受黄河泛滥淤淀，形成湖洼沼地，地形地貌复杂，降雨量预测难度大。加之季风气候的影响，降雨年际及年内分布不均，旱涝灾害频发，严重制约着当地的经济发展。因此选取桓台县为研究区域，数据来源于桓台县水文站。

2.2 时间序列分解

利用matlab 进行编程，以桓台县1979-2018年降雨数据为例，时间步长为月，将时间序列分解为趋势项、周期项、突变项与随机项进行数据挖掘。

（1）趋势项：分别采用累积距平、Mann-Kendall、Hurst 指数等方法进行趋势性分析，特征点法进行趋势项提取。累积距平图如图3所示，Hurst指数图如图4所示，Mann-Kendall趋势分析结果如表1所示。

由图3可得，累积距平图总体较为平稳，存在先降后升的趋势，但不明显。由表1 可得，数据总体呈现微弱上升趋势，但趋势不显著。图4 中，Hurst 指数为0.067 7，H值＜0.5，表明该时间序列具有长期相关性，但未来总体趋势与过去相反。

表1 Mann-Kendall 趋势检验结果Tab.1 Mann Kendall trend test results

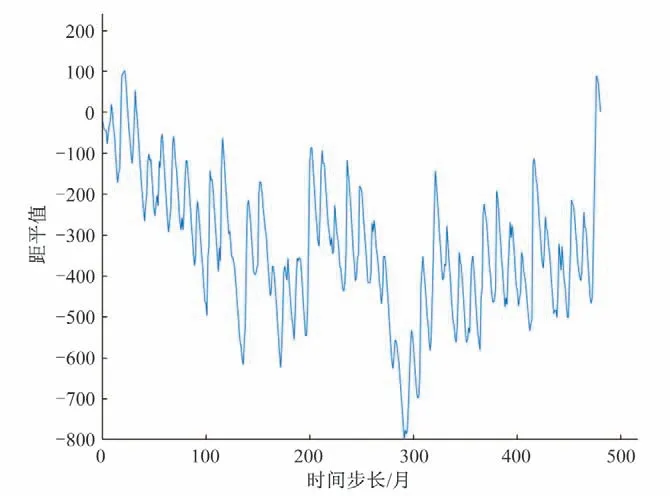
图3 累积距平图Fig.3 Cumulative anomaly

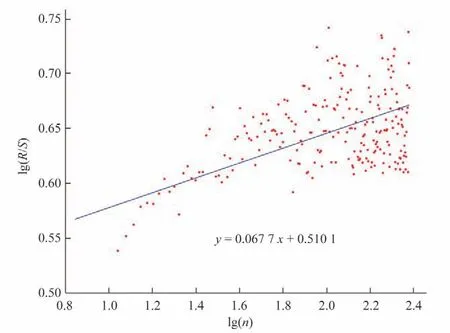
图4 Hurst指数图Fig.4 Hurst index

综合分析可得，桓台县1979-2018年月降雨数据趋势变化较为平稳，存在微弱上升趋势，预测下一时段将呈现微弱下降趋势。

以上为定性分析，现根据特征点法定量分解趋势项。取阈值C=12，将雨量数据进行分段，分段后的特征点利用插值法首尾相连，结果如图5所示。

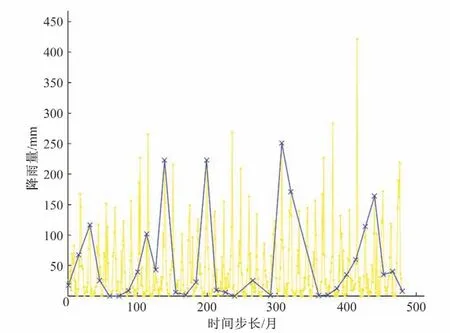
图5 特征点分段图Fig.5 Feature point segmentation

由图5可得，桓台县1979-2018年的月降雨量大致呈现5次丰枯交替现象，为便于直观描述，将各特征点的取值前30%标注为high，中间40%标注为mid，后30%标注为low，如图6所示。对各段斜率进行描述，斜率小于-1标注为骤减，-1～-0.1标注为下降，-0.1～0.1 标注为平稳，0.1～1 标注为增加，大于1 标注为激增。如图7所示。

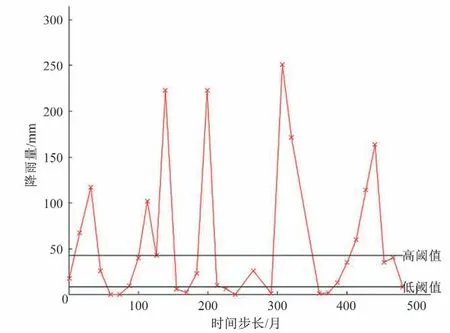
图6 特征点取值描述图Fig.6 Description of feature point value

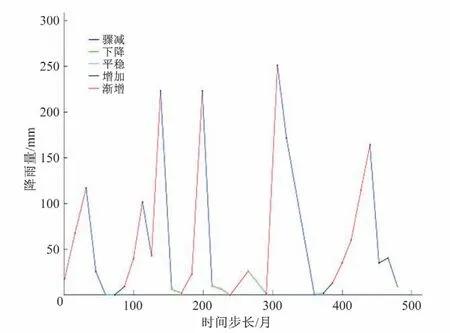
图7 各段斜率描述图Fig.7 Slope description of each segment

经计算插值法误差为79.50，用回归法连接后效果如图8所示（图8中红色数字为各段回归系数）。

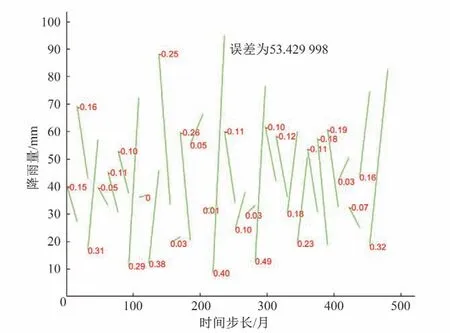
图8 趋势项分解图Fig.8 Trend term decomposition

插值法更为直观，便于描述序列变化情况。回归法误差为53.53，明显小于插值法，因此，选用回归法的结果为时间序列的趋势项。

（2）周期项：使用Matlab 中的小波工具箱得小波方差图，如图9所示。由图9可以看出，桓台县1979-2018年月降雨量的第一主周期为19（月）。以第一主周期时间尺度绘制小波系数图，如图10所示。选取第一主周期小波系数为周期项。

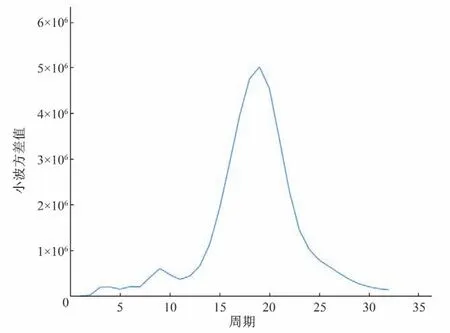
图9 小波方差图Fig.9 Wavelet variance

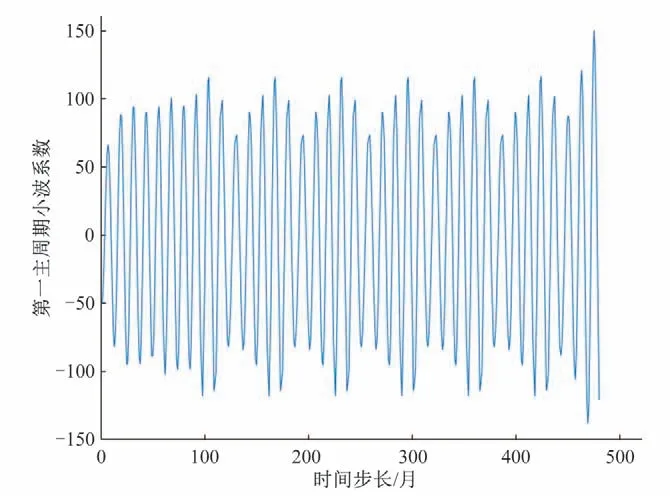
图10 第一主周期小波系数图Fig.10 First principal period wavelet coefficients

（3）突变项：分别采用Mann-Kendall 法、Pettitt 法进行突变性检验，结果如图11、表2所示：

由图11 可得，1979年-2018年的月降雨量突变情况发生少。表2中，突变点检验结果不显著，不能认为产生突变。为避免单个检验方法决策失误，采用文献［4］中突变点判别方法，认为在两种判别方法中均为突变点的月份才发生显著突变。综合分析，认为1979-2018年月降雨不发生显著突变情况，不进行突变项分解。

表2 Pettitt法检验结果Tab.2 Results of Pettitt method

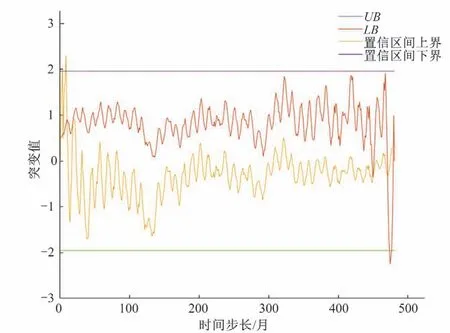
图11 Mann-Kendall突变检验图Fig.11 Mann-Kendall mutation test

（4）随机项：将时间序列减去趋势项、周期项与突变项可得随机项。若随机项的自相关性较小且具有平稳性，说明趋势项、周期项、突变项信息被充分提取。利用Eviews 软件对随机项进行自相关（AC）、偏自相关（PAC）检验，结果如图12所示。

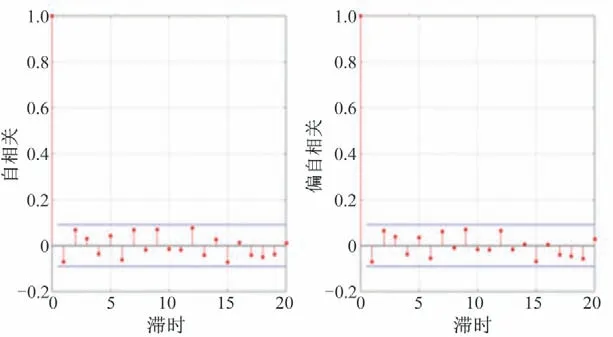
图12 自相关图Fig.12 Autocorrelation diagram

由图12得，AC值与PAC值始终围绕零轴小范围波动，进一步进行单位根检验，得P值 为0、AIC为10.418 02、SC为10.54212、LogL为-2 423.818。由自相关与单位根检验结果可知，随机项不存在单位根，为平稳时间序列。趋势项、周期项、突变项信息已被较为充分提取。

2.3 时间序列预测

2.3.1 随机项预测

为便于验证预测结果，以1979-2014年432 组月降雨量数据为率定数据，2015-2016年月降雨量数据为验证数据，对2017-2018年月降雨数据进行预测。

随机项预测分别采用NAR和NARX［20］神经网络预测法。

（1）NAR 神经网络预测：构建经遗传算法优化的NAR 神经网络，经率定，滞后阶数取18，中间层个数取8，训练集、测试集和验证集比例取70∶15∶15。所构建神经网络模型的回归系数图、误差图、预测结果图如图13～15所示。

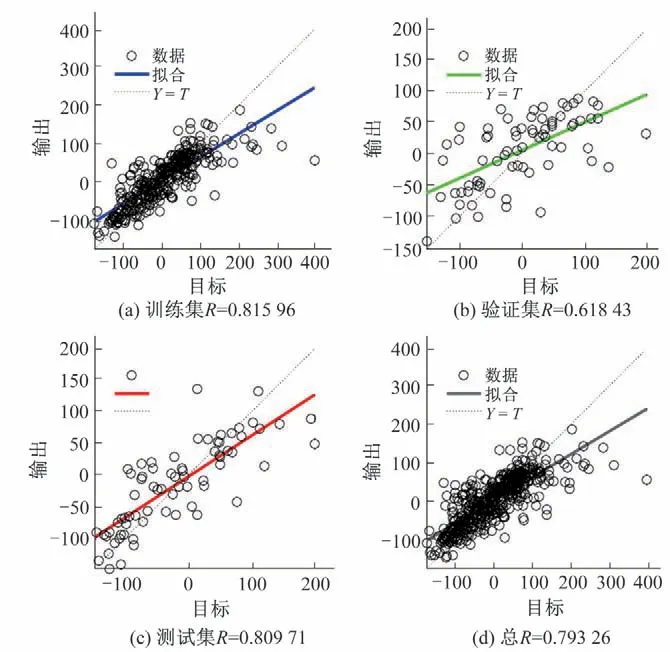
图13 神经网络回归系数图Fig.13 Regression coefficient diagram of neural network

由图13 知，神经网络模型回归系数较高，总回归系数0.793 26，训练集回归系数0.815 96。由图14 知，误差集中分布于0附近，多为小误差，大误差较少。

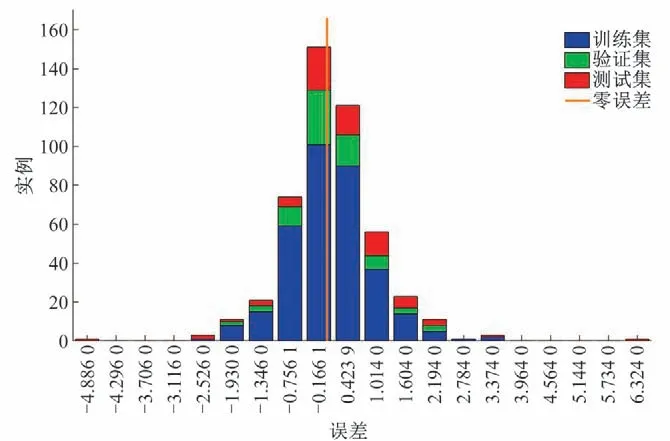
图14 神经网络误差图Fig.14 Neural network error chart

（2）NARX 神经网络预测：为了验证DMAF模型预测结果的合理性，采用NARX神经网络随机项预测法，结果见图16。

2.3.2 时间序列的总体预测

将图15 和图16 的预测结果，分别与所对应的趋势项和周期项相加，得到基于NAR 和NARX 神经网络的2017-2018年月降雨的预测结果，见图17。其中，模型预测误差16.79%，NARXANN预测误差20.05%，直接预测误差41.62%。

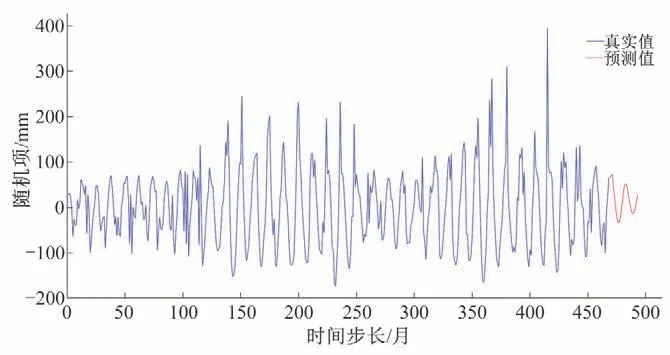
图15 基于NAR神经网络随机项预测结果图Fig.15 Random term prediction result chart based on NAR neural network

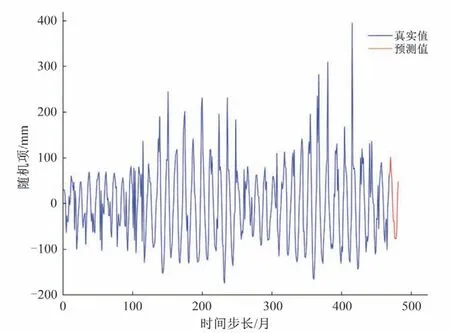
图16 基于NARX神经网络随机项预测结果图Fig.16 Random term prediction result chart based on NARX neural network

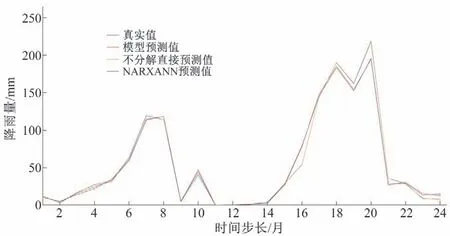
图17 预测结果对比图Fig.17 Comparison chart of prediction results

3 结果分析与讨论

3.1 结果分析

（1）时间序列挖掘：由图3和表1可知，桓台县1979-2018年月降雨量数据有微弱的上升趋势，此结论与文献［2］相符。由图3 可预测未来将呈微弱下降趋势，由图9 可知，其第一主周期是19（月），由图11与表2可知，数据不存在明显的突变情况。

（2）时间序列预测精度：由图17 可知，与1979-2018年月降雨量的实测数据相比，基于NAR 和NARX 神经网络的预测误差分别为16.79%和20.05%。利用NAR 神经网络直接预测法进行时间序列的总体预测（结果见图17），预测结果误差较大（为41.62%）。因此，上述3 种预测方法，基于NAR 神经网络随机项预测方法获得月降雨数据的精度最高。

3.2 讨 论

（1）关于降雨时间序列的数据挖掘与预测的关系：降雨时间序列受趋势、周期与突变等因素影响，复杂多变，数据挖掘能为数据预测提供信息支撑，数据预测结果也能验证挖掘信息的准确性。而现有水文数据挖掘与预测方面的文献［2-5］，未见有基于水文数据挖掘的预测研究，即没有建立数据挖掘与预测的紧密联系，而是直接预测。创新性地提出了DMAF 模型，将降雨时间序列分解为趋势项、周期项、突变项及随机项，并对各项进行数据挖掘，同时建立NAR 神经网络模型对随机项进行预测，再将预测结果与数据挖掘后的趋势项、周期项、突变项相加得降雨时间序列预测结果，相较于直接预测法，结果更为准确。因此DMAF 模型能在充分挖掘降雨时间序列的基础上，对其进行准确预测。

（2）关于利用DMAF 模型对降雨时间序列长短期预测问题：对研究区域的降雨时间序列进行分解后，利用线性延长方法将趋势项T基于特征点法的末端直线进行延长得到Ty；利用Matlab 小波工具箱Extend 函数将周期项P进行延长得到Py；无特殊情况不考虑突变项；利用经遗传算法优化的神经网络预测随机项得Ry；然后，将延长后的趋势项Ty、周期项Py与神经网络预测所得随机项Ry相加得预测结果。因降雨时间序列变化复杂，线性延长特征点法末端直线只能在短期满足精度，DMAF模型适用于降雨时间序列的短期预测。

（3）关于利用DMAF 模型对降雨时间序列预测的步长问题：桓台县1979-2018年的480 组月降雨数据，时间步长为月，若降雨数据能满足一定的时间步长，研究提出的DMAF 模型还能对实时数据（30 min 或1 h 等步长）、周数据、年数据等进行挖掘及预测。

（4）DMAF模型对流域的选择没有严格要求，因不考虑流域温度、下垫面条件、海陆位置、流域河流结构等因素，不同流域水文数据均能采用本模型进行数据挖掘与预测。

（5）周期项由第一主周期小波系数确定，随机项为原始数据减去趋势项、周期项与突变项所得余项，两者存在负值是合理的，单位为mm。

4 结 论

以桓台县1979-2018年月降雨量数据为例，构建了DMAF模型进行数据挖掘与预测研究，主要结论如下。

（1）DMAF模型能在充分挖掘降雨时间序列的基础上，对其进行准确预测，模型将时间序列分解为趋势项、周期项、突变项与随机项，相较直接预测准确度较高。桓台县1979-2018年月降雨量数据挖掘与预测的结果表明，数据有微弱的上升趋势，预测未来将呈微弱下降趋势，其第一主周期是19（月），数据不存在明显的突变情况。对桓台县2018年月降雨数据进行预测，预测值与真实值较为接近，预测结果误差较小，为16.79%。

（2）DMAF模型短期预测精度较高，不适宜长期预测。

（3）DMAF模型的推广性较强，能对实时数据、周数据、月数据、年数据等进行挖掘与预测。

（4）DMAF模型的流域通用性较广，对流域的选择没有严格要求，可适用于其他流域数据。 □