胶东半岛典型流域地表水文过程变化及其归因分析

王宏宙，孙善磊，王 洁，于志国，闫桂霞，周舒佳，毕早莹

（1.南京信息工程大学气象灾害教育部重点实验室，南京210044；2.常州市金坛区气象局，江苏常州213200）

0 引 言

随着社会经济的快速发展和人口的不断增长，人类对水资源的需求增大，水资源短缺问题日益加剧，已成为影响社会经济可持续发展的重要约束条件［1］。作为水文循环的重要环节，地表水文过程始终与水资源的合理开发利用密切相关；因此，了解和认识地表水文过程对全球变化的响应已成为水文、气候等科学研究的热点科学问题［2-4］。

地表水文过程始终与气候变化和人类活动密切相关［5-8］。如降水直接决定了地表水分供给；温度、风速、相对湿度和辐射等气候要素通过改变蒸散发（ET）过程，影响地表水分支出［6］。而人类活动通过改变流域下垫面特征（如水利工程设施的修建、生态恢复、城市扩张等）影响产汇流机制及地表水文过程［6-8］。在全球气候变化加剧的背景下，人类改造自然环境的能力不断提高，使得区域乃至全球水文循环变化变得愈加复杂。为厘清相关机制，学者们采用各种手段和方法，剥离了不同气候要素变化和人类活动对径流、ET的影响，取得了大量研究成果［9-13］。常用的区分气候变化和人类活动影响的手段有：流域对比分析法［9］、敏感性分析［10］、陆面模式法［11］、水文模型法［12］及弹性系数法［13］等；但这些方法存在一定的局限性。比如，流域对比分析法很难找到两个完全一致的流域，且费时费力［9］；而水文模型和陆面模式法对驱动场要求较高，耗费计算机时，尤其对大流域［11，12］；弹性系数法未考虑影响因子间相互作用对水文过程的影响，存在不确定性［10］。近来，Sun等［14］原创性地提出了一种基于敏感性试验的多控制因子联立求解方法，可以有效而准确地剥离各因子对水文分量变化的影响，已被成功应用于鄱阳湖流域和中国西南地区。另外，自Budyko 框架理论提出以来，因其需要资料少、结构简单、物理机制明确、模型参数少（仅1 个流域特征参数），已被广泛应用于水文循环变化研究［15，16］；更重要的是，Budyko 参数反映了流域特征，为综合研究气候变化和人类活动对水文循环的影响提供了重要的模型工具。

胶东半岛包括青岛市、烟台市、威海市及潍坊市的一部分，总面积42 680 km2，为我国北方主要的经济技术开发区。胶东半岛区域水系多发源于中部山地，河川径流洪枯期悬殊，径流集中在汛期；由于特殊的地形地貌和持续性少雨，该区域已出现严重的水资源短缺问题，严重制约了胶东半岛经济发展［17-23］。近年来，胶东半岛地区气候变化加剧，加之人类活动规模增大、强度增强，造成了该地区水土流失严重、涵养水分能力降低等一系列环境问题［19，23］。目前对胶东半岛流域水文循环变化的关注较少，尤其是ET变化尚不清楚；虽然少数学者对该地区径流变化特征进行了研究［17-23］，但依然缺乏关于水文循环变化机理的定量化归因分析。因此，系统分析胶东半岛气候和水文过程变化规律，并揭示气候变化和人类活动在其中的作用，已成为理解本地区水文循环变化机制、改善水资源管理措施及合理开发利用的当务之急。

综上，拟选取胶东半岛4个典型流域，详细分析气候和主要陆面水文分量（如ET和径流）的变化特征，并采用Budyko 方程结合多控制因子联立求解方法，定量化估算气候变化和人类活动（以Budyko 参数表示）对ET和径流的影响，以此探讨胶东半岛地表水文循环变化机理。本研究有望为应对胶东半岛水资源短缺，建立科学的水资源管理制度，及维持社会经济健康发展提供重要的定量化信息。

1 资料与方法

1.1 资料及处理

气象要素采用国家气候中心提供的胶东半岛1961-2010年间16个常规气象站（图1）的逐日降水（mm）、日照时数（h）、10 m风速（m/s）、相对湿度（%），及最低（oC）、最高（oC）和平均温度（oC）观测资料。由于缺少辐射观测，利用日照时数和Allen等［30］推荐的公式计算净辐射。水文要素为1961-2010年4 个水文站（图1）的逐年径流数据（m3/s），来自烟台市水文水资源勘测局和青岛市水文水资源勘测局。采用1 km×1 km SRTM 数字高程模型（http：//westdc.westgis.ac.cn）和ArcGIS 10.2 水文分析工具，提取流域边界和面积；然后，根据流域面积估算地表径流（mm）。考虑世界粮农组织推荐的FAO56 Penman-Monteith 公式具有明确的物理含义，拟采用该公式估算各气象站点PET，详见Allen等［24］。采用流域水量平衡方法估算流域不同年代ET；首先，将1961-2010年分为1961-1980年（基准期）、1981-1990年（1980s）、1991-2000年（1990s）和2001-2010年（2000s）4 个时段，采用反距离权重法对年降水（P）进行空间插值，获得各流域不同时段年降水；以P减去径流获得ET。气候和水文分量年代变化，以各时段减去基准期表示。

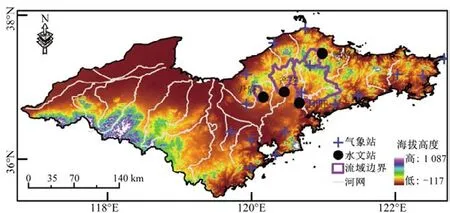
图1 流域、气象站和水文站分布Fig.1 Locations of the selected 4 basins，weather and hydrological sites

1.2 Budyko方程

由Budyko 假设，ET受水分供给（即降水）和能量供给（即PET）的共同影响；流域尺度上，降水和PET之间存在耦合平衡关系。在此基础上，傅抱璞［25］和Yang 等［26］基于无量纲分析和数理方程，提出了包括流域特征影响的Budyko模型。本研究采用Yang等［26］的方程，

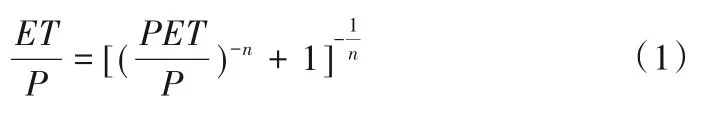
一般，n越大，ET消耗降水越多，反之相反。利用降水、PET和ET，分别拟合基准期、1980s、1990s 和2000s 参数n，即n基准期、n1980s、n1990s和n2000s。关于径流（Q）的方程可写为，

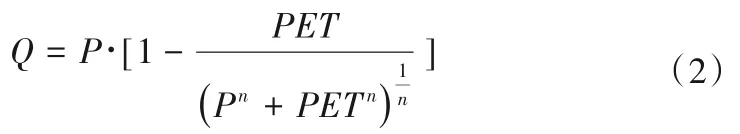
1.3 归因方法

为减少影响因素间相互作用带来的不确定性，拟参考Sun等［14］提出的基于敏感性试验的多控制因子联立求解方法，设计试验，分离各因子对ET和径流变化的贡献。具体如下：首先，由影响ET或径流的气候因子（温度、净辐射、相对湿度、风速和降水）和参数n，设计7 组试验，其中1 组基准试验（EXP-BASE）和6 组敏感性试验（EXP_non-Y，Y为影响因子），具体见表1。以1980s的温度试验（EXP_non-Tave）为例，温度设置为基准期，净辐射、相对湿度、风速维持在1980s，采用FAO56 Penman-Monteith 公式计算PET，然后，将计算的PET、1980s 降水和n1980s代入方程（1）或（2），估算EXP_non-Tave 的ET或径流。最后，联立方程，获得各因素对水文分量变化的贡献。以EXP_non-Y为例，其对应的ET或径流（相对于基准期）变化可认为是除Y以外的其余因子共同引起的，可表示为：

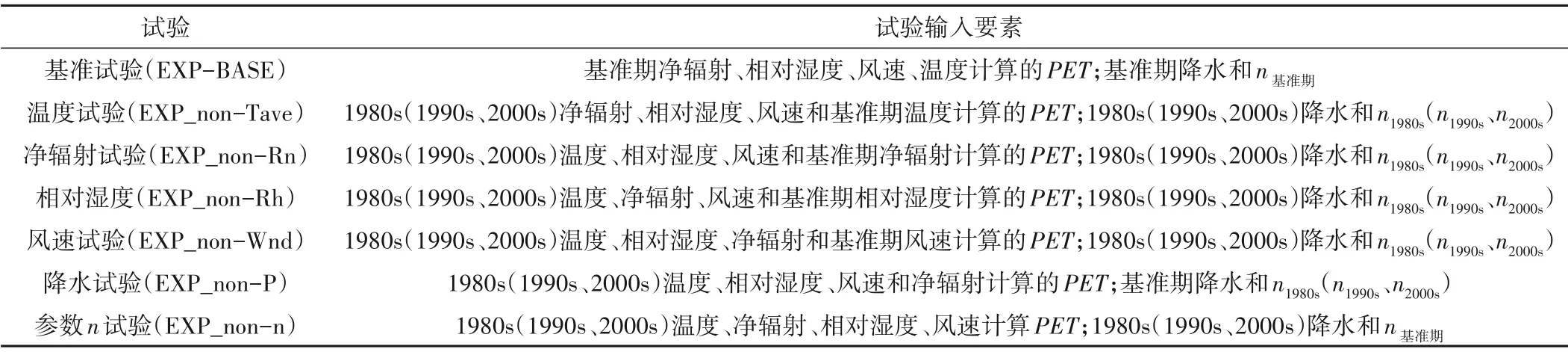
表1 试验设计Tab.1 Configurations of experiments

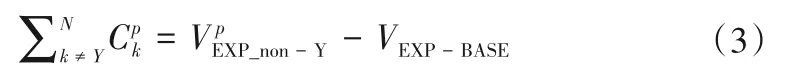
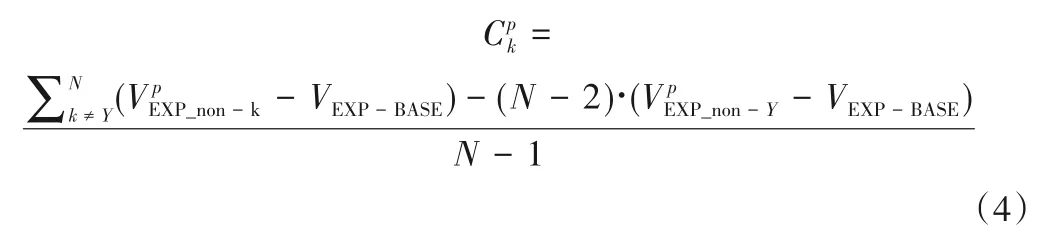
需要指出的，PET对ET或径流变化的贡献为温度、辐射、相对湿度和风速贡献之和。为确定ET、径流变化的主控因子，首先，判断参数n的贡献是否大于气候变化（即降水和PET贡献之和）；如果大于，则ET或径流变化的主控因子为参数n；相反，气候变化影响较大且降水贡献大于（小于）PET，则主控因子为降水（PET）。

2 结果分析

2.1 降水、PET及参数n变化特征

由图2（a），各流域基准期降水基本在700 mm 左右，以团旺和臧格庄较大（＞760 mm）；PET均在1 000 mm以上，且臧格庄最大（1 118.40 mm）；产芝、团旺、尹府和臧格庄的基准期参数n分别为1.40、1.34、1.11 和1.42，说明产芝和臧格庄有较多的降水通过ET的形式被耗散，而尹府有较少的降水被ET耗散。图2（b）为降水较基准期的变化，总体而言，各流域不同时段降水均减小，特别是1980s 和1990s（除尹府）减小较大（＜-100 mm）；2000s 降水依然偏少，但减小幅度基本在50 mm 以内。由图2（c），PET变化表现出一定的区域性差异；在产芝、团旺和尹府，1980s 和1990s 的PET增加，但2000s 下降，变化幅度均小于30 mm；臧格庄各时段PET均减小，且1990s 和2000s 减小明显（＜-55 mm）。较基准期，各流域参数n在各时段一致性地增加［图2（d）］，说明由于人类活动的增强，ET分配的降水增加；除个别时段外，参数n的增幅均大于0.5，尤以产芝1980s 和2000s增幅最大，在1.0以上。

图2 不同时期各流域主要水文气候分量和参数n及降水、PET、参数n较基准期的变化Fig.2 Values of the major hydro-meteorological elements and parameter n over the 4 basins during each period and changes in precipitation，PET and parameter n relative to the baseline period

2.2 归因方法评估

在进行归因分析之前有必要对剥离因子贡献的方法进行评估，本研究采用各因子贡献之和与观测的ET、径流变化散点图，以及相关系数（R）、趋势系数和均方根误差（RMSE）等指标，结果如图3。很明显，该方法剥离的各因子贡献之和与观测的ET、径流变化几乎处在1∶1 线上。由定量化指标，各因子贡献之和与观测的ET、径流变化的R几乎为1，RMSE为5.12 mm，拟合趋势线的趋势系数也近乎为1；均说明该剥离因子贡献方法可以较为准确地估算各影响因子对ET、径流变化的贡献。

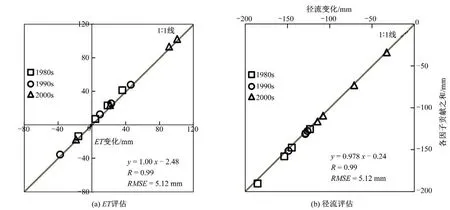
图3 归因方法评估Fig.3 Validation for the selected attribution method

2.3 蒸散发变化及其归因

如图2（a），尹府流域基准期ET为454.98 mm，其他流域均在500 mm 左右，以臧格庄最大，为550.53 mm。由图4（a），就产芝、团旺和尹府，各时段ET均增加，且产芝和尹府2000s的增加最明显（～100 mm）；相反，臧格庄不同时段ET均减小，且1990s最大，为-35.60 mm。图4（b）～（d）为各流域降水和参数n对不同年代ET变化的贡献。1980s，由于降水减少，产芝和尹府ET减小了～95 mm，而团旺和臧格庄减小了～80 mm；随着PET增大，产芝、团旺和尹府ET增大（＞10 mm），其中尹府增加最大（20.51 mm），需要注意的，尽管臧格庄PET减小，但其贡献为正，这可能与剥离贡献方法的误差有关；就参数n，其对ET变化的贡献均为正，且大于50 mm，尤以在尹府最大（111.55 mm）。1990s，降水贡献均为负，除尹府外，其他3个流域的贡献率均大于65 mm，且臧格庄最大（-99.94 mm）；由于产芝、团旺和尹府PET增加，ET增大（＜15 mm），而臧格庄PET的减小使得ET略微减小。2000s，降水对ET变化的贡献依然为负（＞-25 mm）；PET的减小使得各流域ET减小（＞-12 mm）；随参数n的增大，各流域ET不同程度的增大，其中产芝和尹府的贡献大于105 mm，而臧格庄的贡献最小（16.46 mm）。由图4（b）～（d），臧格庄各时段PET、参数n对ET变化的贡献均小于降水，故臧格庄1980s、1990s和2000s的ET变化主要归因于降水的减少；与之相反，其他流域各时段均显示参数n的贡献最大，故产芝、团旺和尹府各时段ET变化的主控因子为参数n。另外，需要指出的是，臧格庄ET变化主控因子不同于其他流域，其原因可能为降水［图2（b）］、参数n［图2（d）］的变化幅度以及ET对它们的敏感性（即单位降水或参数n变化引起的ET变化）存在一定区域差异。

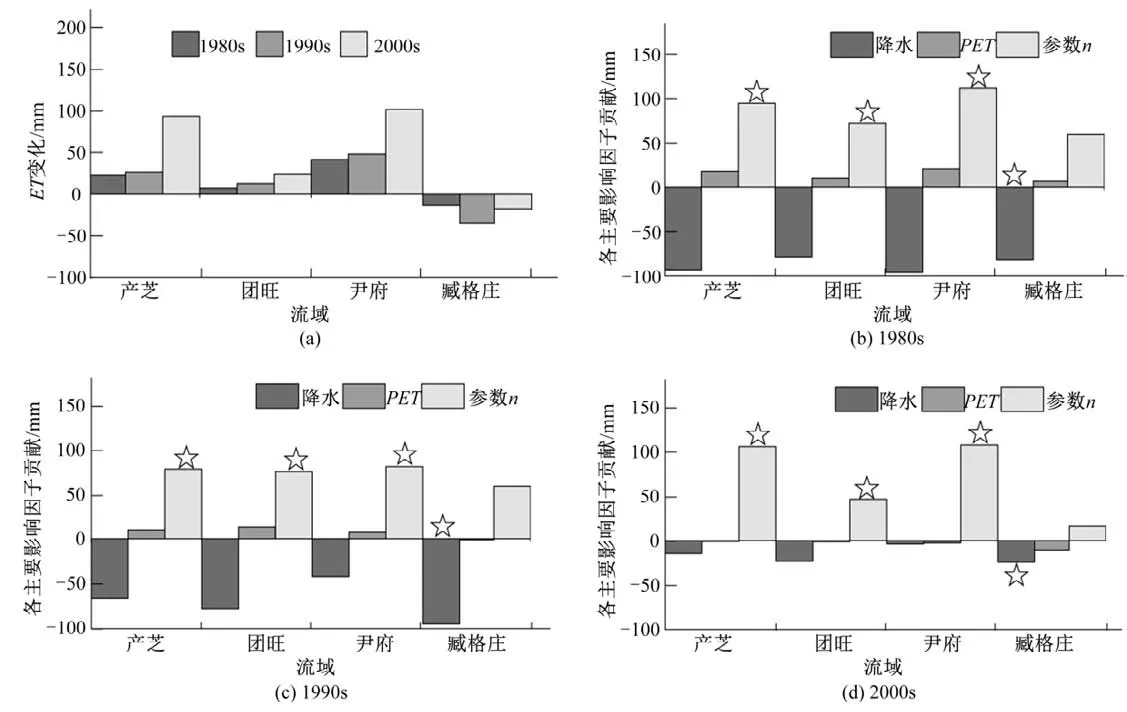
图4 不同时段ET变化及降水、PET和参数n对各时段ET变化的贡献Fig.4 Changes in ET during different periods，accompanied with contributions of precipitation，PET and parameter n

2.4 径流变化及其归因

由图2（a），除产芝基准期径流小于200 mm，其他流域均大于200 mm，且尹府最大，为242.65 mm。就各时期径流变化，各流域均不同程度减小［图5（a）］，1980s 径流下降最大（＜-130 mm），而2000s 下降较小（＞-120 mm）。如图5（b）～（d），1980s，降水减小使各流域径流减小，除产芝外，其贡献率均大于50 mm；由于PET增大，产芝、团旺和尹府径流减小（＞-20 mm）；参数n的增加使各流域径流减小，以产芝和尹府减小最大（＜-90 mm）。1990s，降水对径流变化的贡献为负，其中团旺和臧格庄的贡献较大（＜-60 mm），且以臧格庄最大（-70.11 mm）；随着PET的增加，产芝、团旺和尹府径流减小（＞-15 mm），而臧格庄PET使得径流略微增大。2000s，降水对各流域径流变化的贡献为负（＞-30 mm）；PET对各流域径流变化贡献为正（＜12 mm）；随着参数n的增大，各流域径流不同程度减小，其中产芝和尹府贡献较大（＜-105 mm），而团旺和臧格庄贡献较小（＞-50 mm）。对比各因子对径流变化的贡献［图5（b）～（d）］，可以发现，1980s，产芝和尹府流域参数n对径流下降的贡献最大，而团旺和臧格庄流域降水对径流减小的贡献最大，故产芝和尹府、团旺和臧格庄径流变化的主控因子分别为参数n、降水；1990s 和2000s，除臧格庄主控因子为降水（降水贡献最大），而其他流域均显示参数n对径流变化的贡献最大，故其他3 个流域径流的变化可归因于参数n的增大。值得注意的是，流域间径流变化主控因子存在差异，这可能与降水［图2（b）］、参数n［图2（d）］的变化幅度以及径流变化对它们的敏感性（即单位降水或参数n变化引起的径流变化）的区域性差异有关。

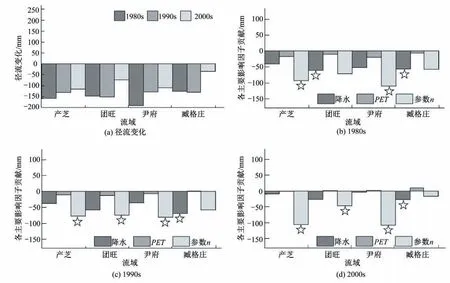
图5 不同时段径流变化及降水、PET和参数n对各时段径流变化的贡献Fig.5 Changes in runoff during different periods，accompanied with contributions of precipitation，PET and parameter n

3 结论与讨论

以胶东半岛4 个典型流域为例，本研究详细分析了各流域降水、PET、ET和径流变化特征，并基于Budyko方程和多控制因子联立求解方法，估算了气候和参数n对ET和径流变化的贡献，开展了归因分析，得到以下结论。

（1）较基准期1961-1980，各流域各时段降水均减小，以1980s 和1990s 减小最大（＜-100 mm）。PET变化表现出明显的区域性差异，产芝、团旺和尹府在1980s 和1990s 增大，而在2000s减小，臧格庄各时段PET均减小，且1990s和2000s减小幅度较大（＜-55 mm）。各流域不同时段参数n均增大，尤其产芝1980s和2000s增加最大（＞1.0）。

（2）定性和定量化指标均显示多控制因子联立求解方法可以较为准确地估算各影响因子对ET、径流变化的贡献。

（3）产芝、团旺和尹府各时段ET均增加，其中产芝和尹府2000s 的ET增加最明显（＞100 mm）；相反，臧格庄不同时段的ET较基准期均减小，且1990s 减小最大（-35.60 mm）。不同时段ET的变化，除臧格庄主控因子为降水，其余流域ET增加均归因于参数n的增大。

（4）各流域径流均减小，1980s 下降最大（＜-130 mm），而2000s 下降较小（＞-120 mm）。产芝和尹府1980s 径流的下降归咎于参数n的增大，而团旺和臧格庄径流减小的主控因子为降水；1990s 和2000s，除臧格庄主控因子为降水，其余流域径流变化的主控因子均为参数n。

通过分析胶东半岛4 个流域不同时段ET和径流（较1961-1980年）的变化，揭示了在全球变化背景下该地区水资源量明显下降。采用Budyko方程和多控制因子联立求解方法对ET和径流变化进行了归因分析，甄别了控制各流域地表水文分量变化的主要因子，有助于各流域制定合适的应对水资源短缺的措施。对于参数n（即人类活动）主导的流域，政策制定者可通过改变人类活动等，减小ET耗散，增大径流量，提高水资源储备；而对于降水变化主导的流域，政策制定者可考虑修建水利工程设施，储备降水，提高水资源利用效率，以减少水资源短缺带来的负面影响。

本研究存在一定的不确定性。如资料的处理：未考虑地表反照率（设置为常数0.23）的时空变化［27，28］估算净辐射，可能会对PET估算造成偏差。气象观测（尤其是降水）经常受仪器和观测场条件的影响［29］，进而给本研究带来不确定性。FAO56 Penman-Monteith 公式：FAO56 Penman-Monteith 公式并未考虑CO2浓度升高对植被生理特征（如气孔导度和植被结构特征）的影响，进而造成PET估算存在偏差［30］。剥离各因子贡献的方法：该方法的核心假设为影响因子的贡献是线性叠加的，但事实并非如此，进而造成一定的不确定性。 □