不同集成模型对小流域短时径流预报的影响研究

林泳恩，杜 懿，孟 越，解河海，王大刚

（1.中山大学地理科学与规划学院，广州510000；2.珠江水利委员会珠江水利科学研究院，广州510000）

0 引 言

准确可靠的短期径流预报对制定防洪减灾应急计划，保障人民生命财产安全具有重要的战略意义和应用价值。随着我国当前水利信息化的大力推进，水文数据的数据量呈现出指数级的增长趋势［1，2］。在如今这个大数据时代，基于数据挖掘技术，从历史经验与海量气象水文数据中提取数据的深度价值，是水文预报发展的一个重要方向［3］。

机器学习是一门研究计算机如何效仿人的学习行为来取得新的知识和技能的学科。机器学习算法可以从数据中自动分析获得规律，并利用规律对未知数据进行预测，因此被广泛应用于数据挖掘、计算机视觉、生物特征识别、网络安全、市场规律分析等领域［4-7］。基于大数据的机器学习能够在不考虑流域汇流过程、下垫面变化、人类活动影响等复杂因素的前提下，构建径流预测黑箱模型，实现对未来河道水量的高效预测。

机器学习中的不少智能算法已广泛应用于水文领域中，比如入库流量预测［8］、地下水预测［9］、水质预测［10］等。关于短期径流预报的文章也有不少［11-15］，但在这些研究中，往往只是建立单一的预报模型，准确率与稳定性均有待提升。集成学习基于博采众长的思想，通过构建并结合多个机器学习器来完成学习任务，能够有效防止过拟合和欠拟合问题的发生，从而改善预测效果。目前集成学习在人脸识别［16］、电力调度［17］、疾病诊断［18］等领域已有不少应用，在水文水资源领域也有一些研究。如王婉琳将集成学习应用于再生水资源配置，得到的配置结果明显优于传统智能优化方法的配置结果［19］。许斌等人将随机森林模型和梯度提升树模型应用于中长期径流预报中，结果显示这两个集成学习模型能有效提高预报的准确度、可靠度和稳定度［20］。马新宇等人的研究结果表明，bagging集成学习模型对于水华的预测能力高于单个BP网络模型［21］。

目前关于集成学习在短期径流预测中的应用研究还比较缺乏，因此本次研究将利用前馈神经网络（FFNN）、长短期记忆神经网络（LSTM）、支持向量回归（SVR）、自回归积分滑动平均模型（ARIMA）以及分类回归树（CART）作为基学习器，分别建立bagging 集成模型、stacking 集成模型、GBDT 集成模型以及AdaBoost 集成模型，实现对安墩水流域小时尺度的径流预测，并通过相关系数（CC）、平均绝对误差（MAE）、平均相对误差（MRE）、均方根误差（RMSE）、纳什效率系数（NSE）、达标率（QR）等指标进行比较分析，探索短期径流预测的研究发展新途径。

1 研究区概况与数据

安墩水，又称安墩河，为西枝江的一级支流，发源于广东省惠东县安迅镇水美村，于惠东县多祝镇水口村汇入西枝江。安墩河流域属于亚热带季风气候，高温多雨、气候湿润，因为受到莲花山脉的影响，其成为惠州市的暴雨中心之一。安墩水流域总集雨面积为404 km2，其中，九洲水文站以上集雨面积达385 km2，流域长51 km，平均比降4.33‰，多年平均径流量54 m3/s，多年平均降水深1 761.5 mm，其中约80%的雨量集中分布在4-9月间。

安墩水流域内共设有梅子坪、洋潭、仓下、松坑、安墩、九洲等6 个雨量观测站，九洲站同时也为该流域内唯一的一个水文观测站。各测站的相关信息如表1 所列，流域内各测站的空间分布情况如图1所示。

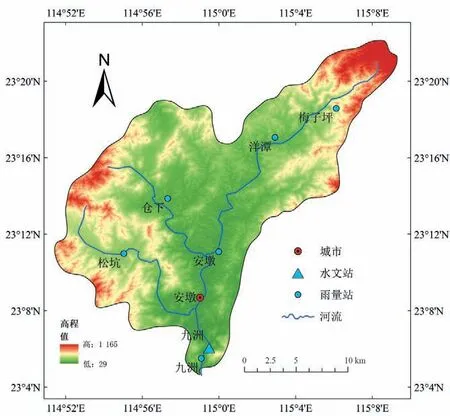
图1 安墩水流域图Fig.1 The map of Andun River basin

表1 安墩水流域内各雨量测站信息Tab.1 Information of rainfall measurement stations in the Andun River Basin

在本研究中，我们使用流域内六个雨量站及一个流量站在1980-2016年的观测数据来进行研究。我们计算了当前时刻流量值与过去不同时刻流量值和平均降雨量值之间的相关系数，结果如图2 所示。由图2 可看出，随着两个流量值的时间差增大，他们之间的相关性不断减少，当滞后时间达到10 h 时，相关系数的衰减速度明显变缓。而当前流量值与前期降雨量的相关性则是随着时间先增大后减小，其中峰值出现在第6 h。基于以上分析，我们最终选择了流域过去10 h 中各小时的降雨量以及流量值作为模型的输入。我们将前80%的数据划分为训练集以用来训练模型，将剩下的20%的数据划分为测试集以用来评价模型的预测效果。

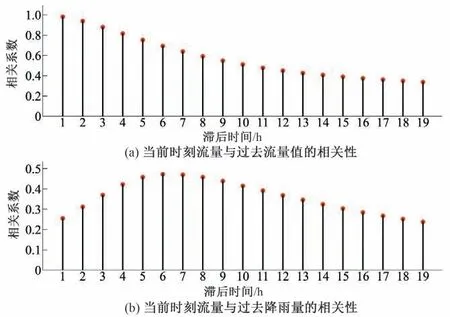
图2 当前时刻流量值与过去不同时刻流量值和平均降雨量值之间的相关性Fig.2 The correlation between the current streamflow and streamflow and average rainfall of the previous times

由于进行的是时间序列的预测以及流量值和降雨量值的量纲不同，为了加快模型训练时的收敛速度以及提高模型的预测效果，本研究在训练模型前先对原始数据集进行了标准化处理，其公式如下：

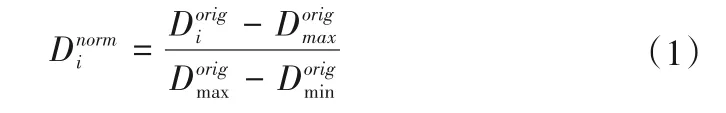
2 研究方法

2.1 建模算法

集成学习（Ensemble Learning）的主要思想是通过一定的方式产生多个子预测模型，再根据特定的策略将所有的子模型进行结合形成最终的集成模型。本次研究将利用前馈神经网络（FFNN）、长短期记忆神经网络（LSTM）、支持向量回归（SVR）、自回归积分滑动平均模型（ARIMA）以及分类回归树（CART）作为集成模型的基学习器，并进一步构造Bagging 集成模型、Stacking集成模型、GBDT集成模型以及AdaBoost集成模型。

前馈神经网络（FFNN）是人工神经网络的一种，其采用一种单向多层结构，整体构架由输入层、隐藏层（一层或多层）和输出层多层网络组成，各层均包含一定数量的神经元。长短期记忆网络（LSTM）是循环神经网络的一种，通过考虑短期和长期状态，LSTM 网络可以识别有价值的输入，并将它们保存在长期状态当中，而当必要时候则可以在长期状态中将这些信息提取出来。支持向量回归（SVR）是为了解决回归问题而根据支持向量机算法演化而来的算法，它将初始数据非线性地映射在高维特征空间以及解决特征空间中的线性回归问题。分类回归树（CART）是一种树构建算法，这种算法主要通过使用二元切分来处理连续型变量，即特征值大于某个给定的值就走左子树，或者就走右子树，这样一步步下去获得最终结果。自回归积分滑动平均模型（ARIMA）是指将非平稳时间序列转化为平稳的时间序列后，将因变量对它的历史值以及误差项的当前值和历史值进行回归建模。目前已有一些研究利用了这几种算法来建立径流预报模型，并取得一定的预测效果［22-26］。

Bagging算法的核心思想是从训练集进行Bootstrap抽样，构造子预测模型，再将所有预测结果进行投票平均。Stacking 算法是一种有层次的集成算法，它的主要思想是先通过不同的方法训练多个不同的弱学习器，然后再训练一个将之前的弱学习器的输出作为输入的高层学习器，它的输出就是最终的预测结果。GBDT 算法通过多轮迭代，每轮迭代产生一个弱学习器，每个学习器在上一轮学习器的残差基础上进行训练，以达到不断减少预测误差的目的。AdaBoost 算法在训练每个弱学习器时，都会根据上一个弱学习器来改变训练样本的权重，最后再通过一定方式将所有弱学习器组合起来。

2.2 评价指标

采用相关系数（CC）、平均绝对误差（MAE）、平均相对误差（MRE）、均方根误差（RMSE）、纳什效率系数（NSE）、达标率（QR）作为评定模拟精度的评价指标。具体为：

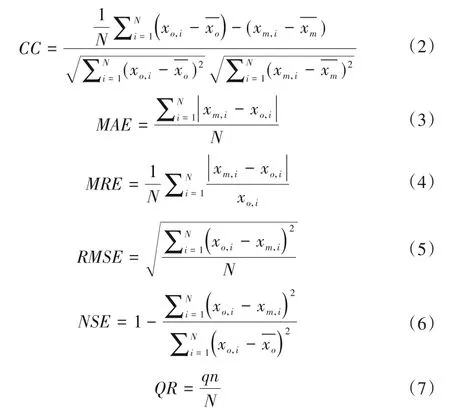
式中：xo，i和xm，i分别为实测值和模型预测值和分别为所有实测值的均值和所有模型预测值的均值；N为总样本量；qn为及格预报的数量，即相对误差小于20%的预报。

3 预测结果分析

图3展示了bagging 模型、stacking 模型、GBDT 模型以及Ad⁃aBoost 模型在预测未来1 h 径流时的性能，其中左边一列4 张图为在训练期的结果，右边一列4 张图为在测试期的结果。不难发现，在训练期GBDT 模型要明显优于其他3 种集成模型，其预测值与实测值之间更加的接近，且决定系数R2最高，为0.997 9；在训练期表现第二好的模型为stacking 集成模型，其决定系数R2为0.990 9。而在测试期，GBDT 模型的预测效果是最差的，决定系数R2仅为0.936 6，且拟合直线与1∶1 线偏离较多；而另外3种模型的表现差异不大，其中表现最好的模型为bagging模型和AdaBoost模型，它们的决定系数R2均为0.9860。综合来看，在预测未来1 h 的径流时，AdaBoost 模型的表现是最好的。当预报未来两小时径流时，4 种集成模型表现出相似的预测性能（图略），训练期它们的决定系数R2按顺序分别为0.963 7、0.971 4、0.995 9 和0.961 6，测试期精度均有所下降，他们的决定系数R2分别为0.946、0.941、0.884 和0.947。当预测未来4 h 径流时，这4 种集成模型仍然保持了较好的预测能力，训练期它们的决定系数R2分别为0.894 6、0.909 0、0.843 7 和0.911 5，而测试期的决定系数R2分别为0.845、0.798、0.809和0.826。

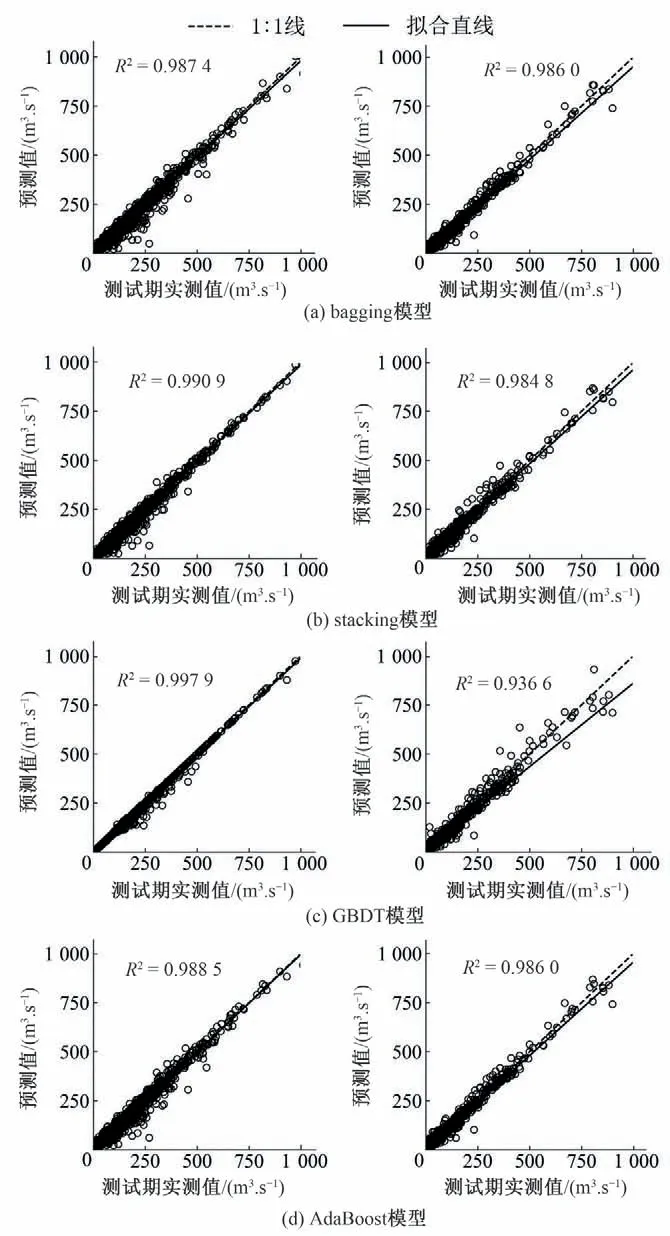
图3 预见期为1 h时bagging模型、stacking模型、GBDT模型以及AdaBoost模型的预测结果与实测值之间的散点分布图Fig.3 The scatter diagram between the predicted results of the Bag⁃ging model，the Stacking model，the GBDT model and the Adaboost model and the measured values when the forecast lead time is 1 hour

分别统计4 种集成模型在测试期中预测结果的6 项精度指标，结果如表2 所示。当预见期为1 h 时，各模型的预测效果排名为：bagging 集成模型＞AdaBoost 集成模型＞stacking 集成模型＞GBDT 集成模型，其中bagging 集成模型的RMSE、MAE、MRE、NSE、QR、CC分别为11.235、4.015、0.086、0.986、0.933 和0.994。当预见期为2 h 时，bagging 集成模型和AdaBoost 集成模型均表现不错，但bagging 集成模型的效果略优于AdaBoost 集成模型，各模型的预测效果排名为：bagging 集成模型＞AdaBoost 集成模型＞stacking 集成模型＞GBDT 集成模型，其中bagging 集成模型的RMSE、MAE、MRE、NSE、QR、CC分别为22.17、8.096、0.141、0.946、0.866 和0.974。当预见期为3 h 时，各模型的预测效果排名为：bagging 集成模型＞stacking 集成模型＞AdaBoost 集成模型＞GBDT 集成模型，其中bagging 集成模型的RMSE、MAE、MRE、NSE、QR、CC分别为31.775、11.795、0.188、0.889、0.809和0.946。当预见期为4 h时，各模型的预测效果排名为：bagging集成模型＞AdaBoost 集成模型＞GBDT 集成模型＞stacking 集成模型，其中bagging 集成模型的RMSE、MAE、MRE、NSE、QR、CC分别为37.865、14.01、0.211、0.845、0.764和0.923。

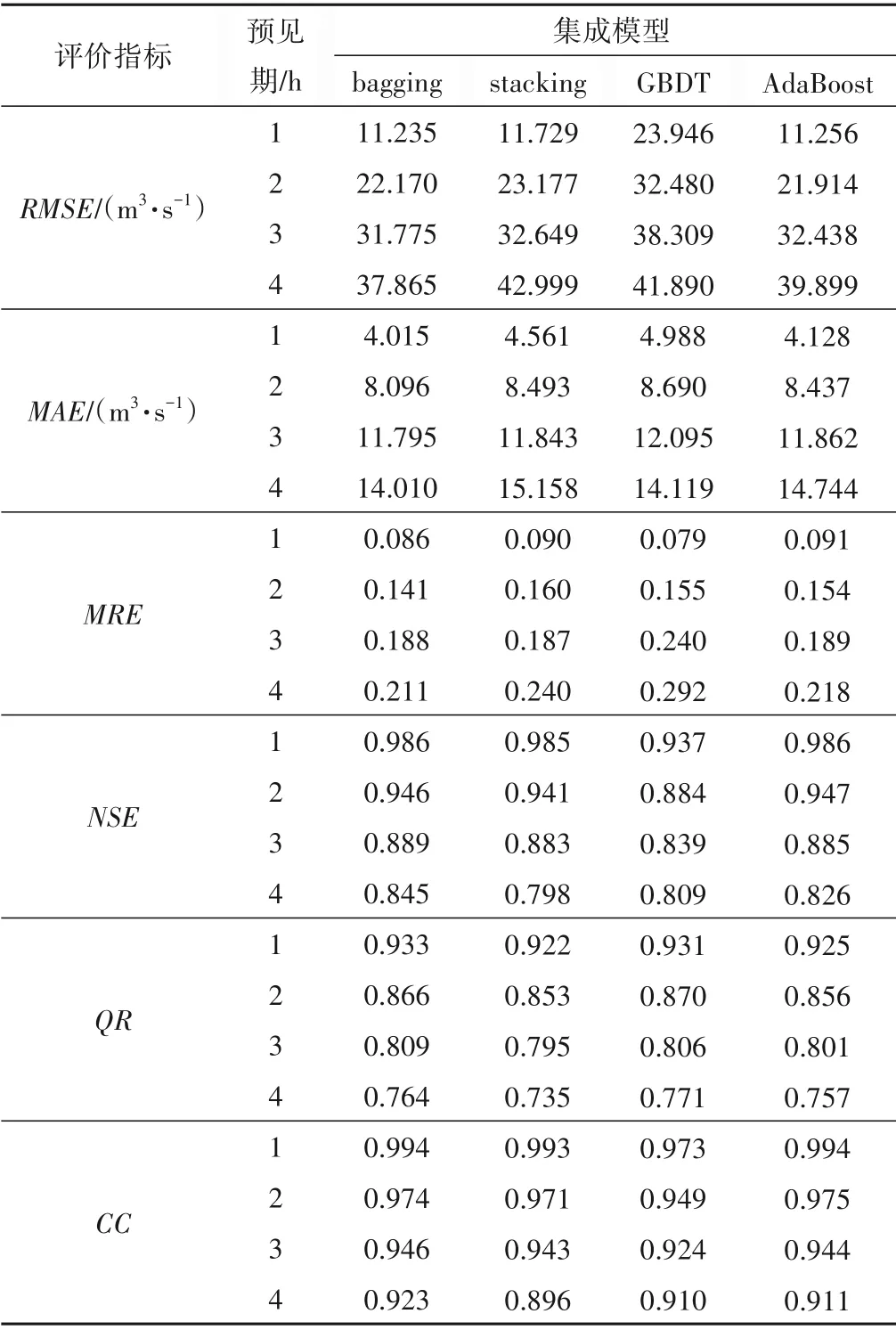
表2 4种集成模型在测试期中的预测效果Tab.2 The prediction performance of the four ensemble learning models in the testing set

随着预见期的增长，4种模型的预测表现均有所下降，这是因为预见期的增长会带来更多的不确定性，从而增加预测的难度。其中bagging集成模型稳定性是最好的，预测性能并没有随着预见期的增长而下降太多，各项指标均能保持在较好的水平上；整体来看，稳定性从大到小排序为：bagging 集成模型＞Ada⁃Boost集成模型＞GBDT集成模型＞stacking集成模型。

Yilmaz 等人［27］的研究指出，最高的2%的流量值体现了河流的洪峰流量，而最低的30%的那些流量值则能够反映河流的基流情况。基于此，本研究将安墩水的流量按照其大小分成了3 个等级：0～28 m3/s 代表基流，28～269 m3/s 代表中等流，大于269 m3/s代表洪水流量。分别计算1 h预见期时4种集成模型对于这3 个级别径流的预测效果，结果如表3 所示。对于基流来说，bagging集成模型和stacking集成模型均有不错的预测性能，而GBDT 集成模型虽然在一些指标上较优，但其RMSE和NSE却比较差，说明其对基流的预测不太稳定，即某些时候预测效果好，而某些时刻效果一般。对于中等流，4种集成模型的效果差异不大，整体来看，各模型的预测效果排名为：bagging集成模型＞AdaBoost集成模型＞GBDT集成模型＞stacking集成模型。对于洪水，AdaBoost 集成模型的表现明显优于其他3 种模型，而GBDT 集成模型的表现则明显差于其他模型。总的来说，这4种集成模型对中等流和洪水均有不错的预测效果，而这一点对于防洪减灾是十分有价值的。

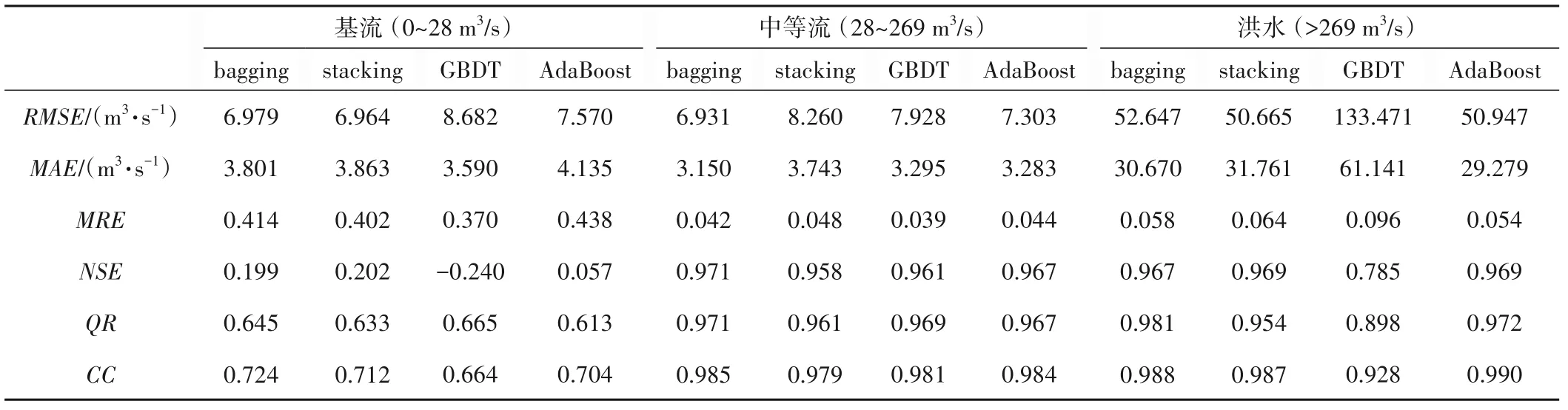
表3 预见期为1 h时4种集成模型对3个级别径流的预测效果Tab.3 The prediction performance of the four ensemble learning models on the three levels of runoff when the prediction lead time is 1 hour

根据安墩水流域九洲水文站的历年逐时流量资料绘制出了测试期内的四场洪水过程，并使用训练好的各集成模型进行了洪水预测，预测情况如图4 所示。这四场洪水中包含了前峰型洪水、后峰型洪水以及多峰型洪水，洪水历时最短的为4 d多，最长的为8 d。从图4中可以看出，对于不同类型、不同级别的洪水过程，这些集成模型均能够合理重现出它们的特点以及随时间的变化，体现了其较高的稳定性和鲁棒性。此外，我们可以发现GBDT 集成模型在洪水起涨初期预测效果较好，但在预测洪峰流量时效果不如另外3种模型。

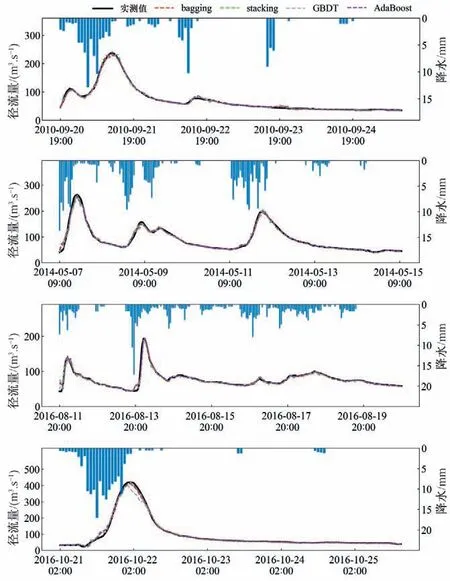
图4 4种集成模型对4场洪水的预测结果Fig.4 Forecast results of four ensemble learning models in four flood events

4 结 语

本研究利用前馈神经网络（FFNN）、长短期记忆神经网络（LSTM）、支持向量回归（SVR）、自回归积分滑动平均模型（ARIMA）以及分类回归树（CART）作为基学习器，分别建立了bagging集成模型、stacking 集成模 型、GBDT 集成模型以及AdaBoost 集成模型，实现对安墩水流域小时尺度的径流预测，并通过相关系数（CC）、平均绝对误差（MAE）、平均相对误差（MRE）、均方根误差（RMSE）、纳什效率系数（NSE）、达标率（QR）等指标进行比较分析，得到如下结果。

（1）若从业务预报中最常用的MRE指标来看，测试期bagging 集成模型对1～4 h 预见期的预测结果分别为0.086、0.141、0.188、0.211；stacking集成模型分别为0.090、0.160、0.187、0.240；GBDT 集成模型分别为0.079、0.155、0.240、0.292；AdaBoost 集成模型分别为0.091、0.154、0.189、0.218，均表明这四类集成模型可用于短期径流预测，且精度尚可，其中bagging集成模型的性能为4种中最优。

（2）随着预见期的增大，从稳定性的角度来看，稳定性从大到小排序为：bagging 集成模型＞AdaBoost 集成模型＞GBDT 集成模型＞stacking集成模型。

（3）对于基流，bagging集成模型和stacking 集成模型均有不错的预测效果；对于中等流，4 种集成模型的预测效果差异不大；而对于洪水，AdaBoost 集成模型的表现明显优于其他3 种模型。

（4）综合以上，对于安墩水流域的短期径流预报，可优先考虑bagging集成模型或AdaBoost集成模型。 □