基于盒维数的雅鲁藏布江流域水系分形维数及影响因素研究

费俊源，吴鹏飞，刘金涛，2

（1.河海大学水文水资源学院，南京210098；2.河海大学水文水资源与水利工程科学国家重点实验室，南京210098）

0 引 言

地貌水文过程研究的一大难点是定量化地描述水系结构特征［1］，而水系结构特征会对水资源空间分布［2］、聚居点规划［3］、地貌演化［4］产生影响，这又使得此特征受到了广泛关注。由于水系的局部与整体间具有自相似性，目前主要使用针对自相似结构的分形理论描述水系结构特征［5，6］。

在分形理论中，分形维数被用于量化描述非规则客体［7］。目前的水系分形特征研究主要依托数字高程模型（Digital Elevation Model，DEM），使用Horton 定律或计盒法获取水系分维数［7，8］。除了针对中小流域的研究［5，9］，以较大流域为对象的水系分形研究大多将流域划分为少量子区域或子流域，单独分析各子区域的分形特征。例如，窦明等［2］依照水资源分区将淮河流域划分为13个区域，发现各区域的水系盒维数能够反映区域的人类活动、土地利用等情况；郑楠炯等［8］将韩江流域划分为9个子流域，发现子流域与整个流域间的分维数接近。但是，上述研究使用的分区较大，且分维数样本数量较少，由于分维数与气象［7］、地形地质［10］间联系紧密，少量的分区不足以充分反映大型流域内气象和地形条件强异质性带来的水系分维数的差异。

本研究以雅鲁藏布江（以下简称雅江）流域为研究区，采用自动化提取方法得到流域内大量不同面积尺度的子流域并通过计盒法获取子流域的盒维数。基于此盒维数数据集分析雅江流域内不同尺度的子流域水系分维数与降水、坡度、起伏度等气象、地形特征的关系。

1 研究区及数据源

雅江流域位于西藏自治区南部，涉及拉萨市、山南市、日喀则市、林芝市4 个地级市部分地区，流域面积24.8 万km2，绝大多数区域海拔＞3 000 m，是世界上平均海拔最高的流域［11］。流域随雅江自西向东延伸，南北方向相对狭窄。流域内降水的空间分布差异大，同时存在干旱、半干旱半湿润、湿润地区［11］。

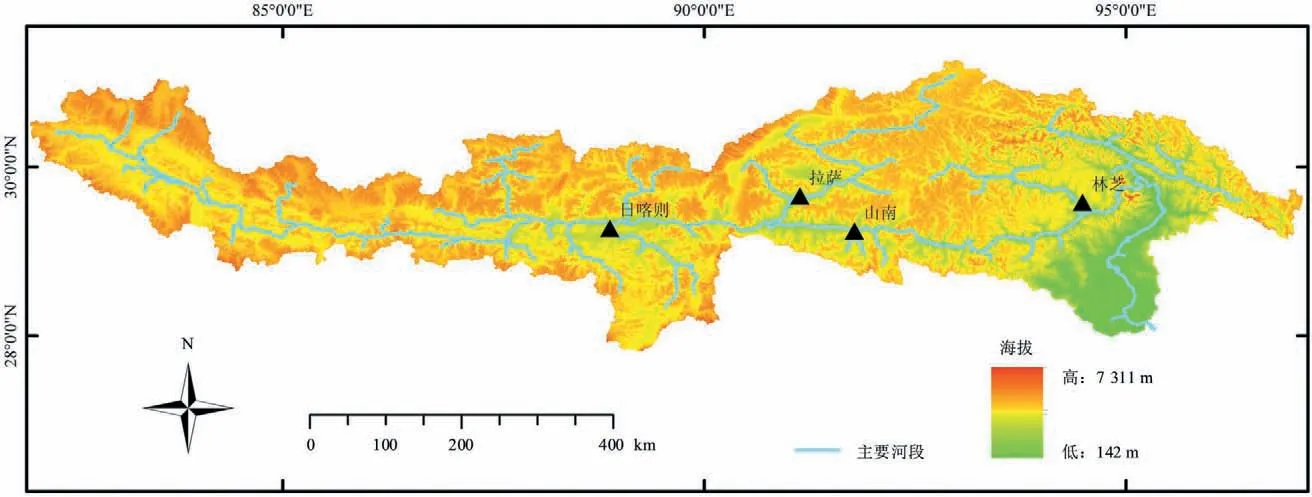
图1 雅鲁藏布江流域概况Fig.1 Overview of Yarlung Zangbo river basin

本研究使用1″（约30 m）分辨率的AW3D30 DEM，数据下载自日本宇宙航空研究开发机构网站（https：//www.eorc.jaxa.jp/ALOS/en/aw3d30）。雅江流域范围由更大范围的DEM，经填洼和流向识别［12，13］，依照雅江出口点提取。研究使用1 km 分辨率青藏高原地区（2000-2015）降水数据，下载自国家青藏高原科学数据中心（http：//data.tpdc.ac.cn），并以此计算出流域各位置的平均年降水量数据。

2 研究方法

2.1 水系及子流域提取

本研究首先对DEM 进行填洼预处理，移除DEM 内因采样误差导致的洼地和平地，再计算每个栅格单元的流向。然后，依据流向累积得到每个单元的上游汇水面积。通过设置临界源面积（Critical Source Area，CSA），提取汇水面积大于CSA的单元作为雅江的主要水系。最后，以水系的全部源点和部分主要干支流交汇节点作为子流域窗口，提取其完整的上游区域作为不同尺度的子流域以供分析。具体方案如下：

首先，自行编程实现由Garbrecht 和Martz［12］提出的算法进行填洼，然后使用Wu 等［13］提出的iFAD8 单流向算法获取单元流向并进一步得到上游汇水面积。

为了综合考虑不同尺度流域间的分形维数差异，以250 km2作为CSA 阈值，提取出雅江流域的主要水系。将所有水系源点对应的上游区域作为最小子流域。再选取2个上游入流汇水面积差异较小（较小入流的汇水面积不得少于较大入流的1/3）的单元作为主要干支流交汇点，提取对应的完整上游流域作为较大面积尺度子流域。值得注意的是，不同尺度子流域间存在嵌套现象，即较小子流域可能被某一较大子流域覆盖。这一方面是为了保证用于分析的是完整流域，另一方面则是为了保证充足的数据量。对此，本研究将所有子流域划分至不同面积区间，主要针对尺度近似的子流域进行分析。尽管依然存在少量处于同面积区间但相互嵌套的子流域，但由于后续使用的都是面平均参数，可以认为这些子流域依然具有代表性。

对于每个子流域，通过设置新的CSA 阈值得到其内部的水系，而本研究使用拐点法确定该阈值［7，14］。拐点法通过检查不同汇水面积阈值下盒维数变化趋势，选择盒维数变化趋势的拐点作为最终阈值。由于本研究使用的子流域数目较多，难以逐个确定每个子流域的最佳阈值，因此使用不同面积阈值下所有子流域的平均盒维数的变化趋势确定拐点，将确定的拐点阈值作为所有子流域的最佳汇水面积阈值。

2.2 盒维数计算方法

首先将栅格DEM 区域划分成大量边长为r的正方形窗口，然后检索出存在水系的窗口数量N（r）。r、N（r）与盒维数D间存在如下关系［15］：

根据上述关系，使用一组r和N（r）数据点绘ln（r）-ln［N（r）］关系图，由最小二乘法拟合的直线斜率的绝对值即为所求盒维数值。由于当r的扩大倍数超过2 时分维数会出现波动［16］，因此研究将r的扩大倍数固定为2，以5 倍栅格单元边长（约150 m）作为初始的正方形窗口边长r。

3 结果与分析

3.1 子流域划分及汇水面积阈值确定

本研究从雅江流域中提取出了356 个子流域，其中依据259 个水系源点提取得到259 个最小子流域，并依据3.1 节的方法选取97 个主要水系节点提取了97 个较大尺度的子流域。然后，以250 个栅格为间距，共计算了9 个CSA 阈值（500～2 500 之间）对应的平均盒维数，结果如图2（a）所示。可以发现，平均盒维数随着CSA 的增大而减小。当以1 500 个栅格（灰色点）为分界点时，汇流栅格数目＜1 500 个（黑色点）和＞1 500 个（空心点）对应的平均盒维数呈现出2 种不同的线性减小趋势，且二者的拟合效果极佳。此外，如图2（b）所示，各CSA 对应的所有子流域盒维数间平均绝对误差和均方根误差都较小，整体与平均值接近，可见采用平均盒维数确定阈值具备代表性。因此，将拐点对应的1 500 个栅格面积（约1.35 km2）作为汇水面积阈值提取水系。

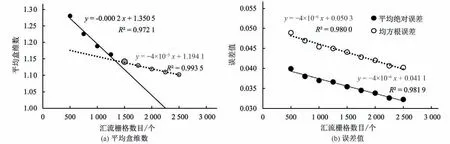
图2 平均盒维数随上游汇流栅格数目的变化关系和所有子流域盒维数的平均绝对误差和均方根误差随汇流栅格数目的变化关系Fig.2 The relationship between the average box dimension and the number of upstream grids and The relationship between the mean absolute error and root mean square error of all sub-basins’box dimension and the number of upstream grids

3.2 分形维数提取结果统计

根据流域的面积大小，研究以500、1 000、2 000、4 000 km2为面积尺度分区节点，分5 个面积区间对356 个子流域的气候、地形特征以及分形维数分别进行了统计（表1）。其中起伏度的定义为流域最大高程和最小高程之差。可以看出，提取出的面积250～500 km2的子流域数目最多，为259 个，也就是有259 个由水系源点提取的最小子流域。值得注意的是，由于DEM单元汇水面积增长的跃进特征，由CSA 得到的水系源点的汇水面积不一定等于CSA 对应的250 km2。其他4 个面积区间内的子流域较少，但也均超过10个。本研究得到的分区盒维数均值最小为1.04，最大为1.17。这一数值范围与邻近流域的研究成果接近［5，16］，属于较小的盒维数范围。水系发育程度越高的区域盒维数越大［16］，由此体现出雅江流域水系发育程度较低。雅江流域的盒维数D≤1.6，表明雅江流域的河流地貌处于侵蚀发育的幼年期［17］。根据表1 中的数据可以发现，盒维数均值存在随面积区间增大而增大的情况，但增幅并不明显。这是由于较大流域包含更多下游河谷区域，该区域水系发育程度优于上游山丘区。此外，不同面积子流域的平均坡度、平均海拔相近，起伏度呈现出随流域面积增大而增加的趋势。

表1 不同面积范围的流域降水、地形特征及分维数统计Tab.1 Precipitation，topographic features and fractal dimension statistics of catchments with different area scales

3.3 分形维数和地形及气象特征的关系

本研究分别分析了5 个面积区间内盒维数随平均坡度、起伏度以及年平均降水的变化关系，并用线性关系、指数型关系、对数型关系拟合了关系函数。对于所有数据组，3 种拟合关系的确定系数差值均小于0.04，因此下文均以最简单的线性关系进行描述分析。

图3 展示了盒维数随平均坡度的变化。在5 种面积区间内，盒维数均呈现随平均坡度增大而减小的趋势。这体现出雅江流域中高地形起伏的上游区域河流处于发育更早期的阶段，越平坦的下游区域河流发育情况越好。此外，随着面积区间的增大，盒维数与平均坡度间拟合的确定系数同样增加。这是由于小流域的水系发育更容易受各类局地因素的影响，大流域更能体现盒维数（或河网密度）与平均坡度间的相关性。

图4展示了盒维数与起伏度之间的相关关系。大致可以判断出雅江流域内子流域存在盒维数随着起伏度的增加而减小的趋势。但整体看来，盒维数与起伏度间的相关性不佳。由于高起伏度地区的平均坡度倾向于更大，这里的变化趋势可以视作图3中盒维数与流域平均坡度相关性的体现。

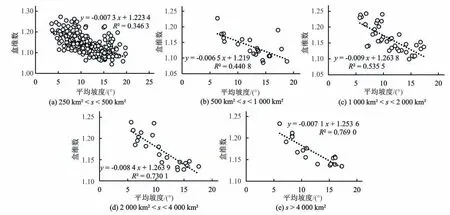
图3 不同面积（s）范围下分形盒维数与流域平均坡度的关系Fig.3 Relationship between box dimension and average slope of catchments with different area scales（s）

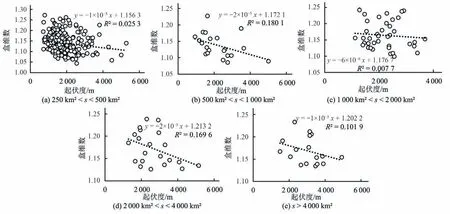
图4 不同面积范围（s）下分形盒维数与起伏度的关系Fig.4 Relationship between box dimension and average topographic relief of catchments with different area scales（s）

图5 展示了不同条件下水系盒维数与年平均降水量的关系。虽然不同面积区间内盒维数与平均年降水量的确定性系数存在波动，但可以发现整体上不同面积区间的流域水系盒维数均呈现出随年平均降水量增大而减小的趋势。研究显示的雅江流域内部的盒维数随年平均降水量的变化趋势与王博等［16］统计全国多个流域得到的湿润半湿润地区分形维数普遍高于干旱半干旱地区的结果不同。结合分形维数与河网密度的对应关系，此差异也许可以类比河网密度与降水量的U 型关系。Abrahams 等［18］证明了河网密度随干旱程度呈U 型关系，即以某一干旱情境为节点，在相对此情境越干旱或越湿润的情况下，河网密度都会增加。因此，可以推断分形维数与降水量可能也呈类似U 型关系，本研究和已有研究发现的特征规律大致分属U 型的两端。在本研究使用的子流域中，当年平均降水量较大（＞600 mm）时，部分子流域并未遵从随年平均降水量增大而递减的趋势，因此可以观察到大量盒维数增大的子流域［如图5（a）、图5（b）、图5（c）］，正是这些子流域导致了相关区间内线性拟合效果较差，也间接佐证盒维数与平均年降水可能存在U型关系。随着面积尺度的增加，受限于流域数目及降水量分布，难以观测到水系分形维数与降水的U型关系。

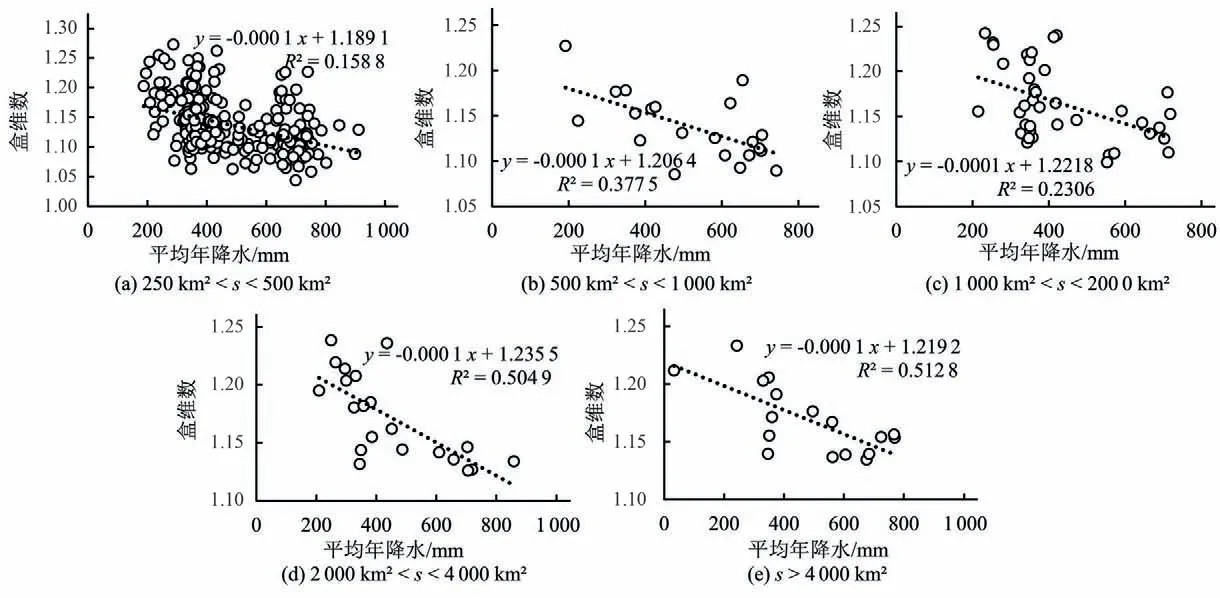
图5 不同面积范围（s）下盒维数与年平均降水的关系Fig.5 Relationship between box dimension and average precipitation of catchments with different area scales（s）

4 结果与讨论

针对已有水系分维研究中样本数量过少的问题，本研究使用自动化处理方法从雅江流域选取了合适的节点，提取出了356个不同面积的子流域，经拐点法确定1.35 km2为最适合雅江流域分形研究的汇流面积阈值。然后使用计盒法计算了子流域的水系分形维数，发现雅江流域的河流处于地貌发育的幼年期。研究还划分了5 个流域面积区间，分别分析了不同面积尺度下盒维数与流域平均坡度、起伏度以及平均年降水量间的关系。结果显示，使用盒维数与平均坡度和平均年降水量间相关性较好，大致呈线性下降的关系，不同面积区间下拟合函数的确定系数则呈现出随流域面积增大而增大的趋势。而流域的分形维数与起伏度间的关系则较差。此外，根据本研究发现流域的盒维数与平均年降水量间关系呈现出非单调趋势，推断盒维数应与河网密度一致，随流域的干旱程度呈U 型关系。其中，较小面积尺度流域的盒维数与平均降水一定程度上呈U 型关系，而此关系在较大面积尺度的流域则不明显，未来仍需要增加不同降水量的大面积尺度流域样本数量做进一步分析验证。

本研究主要关注雅江流域水系分形结构与地形、气象要素的关系。但是部分已有研究表明，水系的分形结构与植被、土地利用等多种其他要素同样存在关联［2，19］，且这些要素与社会、经济关系密切。因此，后续研究需要关注相关领域，将水系分形特征在生产生活中的推广应用。 □