附加直流的低信噪比雷达微振动信号提取 *

林 赟， 章灵涵， 陶 海， 李 洋， 申文杰，王彦平

(北方工业大学信息学院雷达监测技术实验室， 北京 100144)

0 引言

桥梁是重要的交通枢纽，其安全运行对人类安全和经济发展都至关重要。长期运营、车辆超载、环境退化、自然灾害等原因，加速了桥梁结构恶化。有必要在桥梁使用期间进行监测[1]，实时反映桥梁健康状态，避免事故发生。

桥梁形变监测方法可分为接触式和非接触式测量法。典型的接触式测量法比如加速度计、应变计、线性变量差动变压器和光纤传感器等[2-4],形变测量精度高，但是需要把传感器安装在桥梁固定位置处，且仅能对布点位置进行测量。非接触测量法主要包括激光测量法和雷达测量法。激光测量法灵敏度高，但激光穿透性差，受雨雾等环境因素影响较大。雷达测量法具有全天时、全天候工作的优点[5]，可对波束覆盖范围内的目标进行形变监测，毫米波雷达的精度测量可达亚毫米量级，因此使用毫米波雷达是桥梁形变监测重要的手段之一。

雷达信号的相位中包含了目标的距离信息，雷达进行桥梁形变监测的基本原理是对雷达采集的时序数据进行差分干涉获取差分相位信息，通过差分相位积分提取形变量。此方法可以得到高精度的振动幅度和振动频率，是评估桥梁健康状态的重要参数。然而桥梁监测时，当距离较远或振动点雷达反射信号较弱时，信号信噪比低，信号噪声带来的相位误差使得形变量提取误差大。因此如何在低信噪比的条件下正确提取微振动信号特征是目前桥梁形变监测中的重要研究方向。

对差分干涉得到的形变量进行滤波是雷达振动信号去噪的主要方法。主要去噪方法有：奇异值去噪法[6]，该方法使用SVD对矩阵分解，奇异值差分谱进行降噪处理后结合S变换进行时频分析；自适应噪声抵消方法[7]，该方法对信号通过改进的变步长LMS算法对滤波器权系数进行调整，分离信号和噪声；小波变换法[8]，该方法多尺度分解信号，利用噪声和信号在不同尺度的小波分解的不同特征进行去噪。Huang等人提出经验模式分解(Empirical Mode Decomposition, EMD)[9]可以将复杂信号分解为一系列有限小的本征模态函数，具有自适应性，较好去除噪声和目标提取效果，然而会有模态混叠的现象；差分相乘共轭法[10]，该方法利用雷达回波一维高分辨处理后进行差分运算与当前时刻复共轭相乘后去除杂波影响，准确提取微振动信号。

上述方法都是对差分干涉相位积分得到的形变量进行去噪。然而，在低信噪比条件下，信号噪声带来差分相位噪声，当噪声较大时，差分相位可产生缠绕。这样的差分相位缠绕具有随机特性，难以利用邻近差分相位的关联性直接进行解缠绕。对缠绕后的差分相位积分，反演得到的形变量可产生跳变，无法准确反映真实形变量，且破坏了形变信息，这种形变误差也难以采用上述滤波方法去除。

针对低信噪比条件下，噪声引起雷达振动信号差分干涉相位缠绕的问题，本文提出基于附加直流的微振动信号提取方法。该方法通过在信号中附加幅度值远大于实际信号幅值的直流信号，约束差分相位，使其不发生缠绕，从而解决传统方法中的形变量跳变问题，以有效提取振动特征。

本文后续安排如下：第1节对低信噪比环境下的微振动信号进行信号建模；第2节对附加直流微振动信号提取方法进行论述；第3节通过仿真实验和实测数据验证了本文方法的有效性和正确性；第4节对本文进行了总结。

1 微振动目标信号模型

雷达观测几何如图 1所示，雷达位置固定，P为振动点，雷达以一定的脉冲重复频率发射信号，P点的反射信号被雷达接收机接收，得到随时间变化的二维雷达信号。

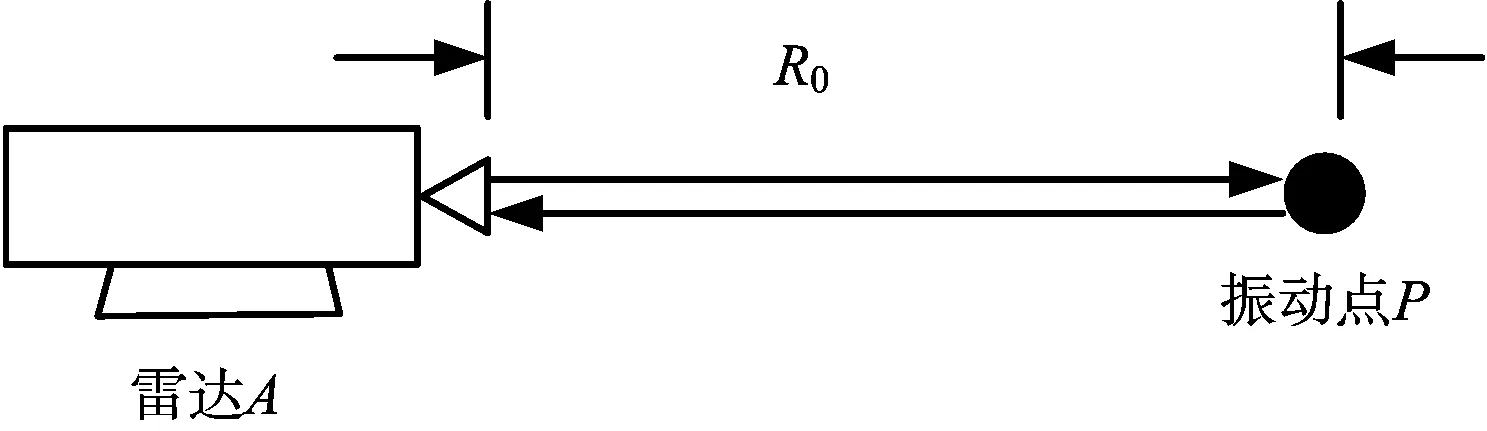
图1 雷达振动监测几何图

假设雷达发射调频连续波信号，其信号波形可以表示为

St(t)=exp(jπKrt2+j2πfct)

(1)

式中，fc为发射信号中心频率，Kr为调频率，t为快时间。雷达一定的脉冲重复频率发射信号，接收到的回波信号表达式为

Sr(t,τ)=Ap·exp(jφp)·

(2)

式中，τ为慢时间，符号*表示共轭，Ap·exp(jφp)为振动点的复反射系数，t0表示信号从目标返回的时间延时，由于振动点的振动，延时是关于慢时间τ的函数，t0的表达式为

t0(τ)=2R(τ)/c=2(R0+Mcos(2πfvτ))/c

(3)

式中，c为光速，R为目标与雷达之间的瞬时距离，是关于慢时间τ的函数。振动点与雷达的中心距离为R0，振动点在雷达视线方向作振幅为M、频率为fv的简谐振动。

对回波信号(式(2))作傅里叶变换和残余视频相位校正处理，得到以下脉冲压缩信号：

Sr(t,τ)=Ap·exp(jφp)·sinc(Br(t-t0))·

exp(-j2πfc·t0)

(4)

式中，Br为发射信号带宽，sinc为sinc函数。

取目标所在距离R0处的慢时间信号，即

Sr,t=2R0/c(τ)=Ap·exp(jφp)exp(-j2πfc·t0)

(5)

将式(3)代入式(5)，可得到

(6)

式中，λ=c/fc为发射信号波长。

式(6)代表的信号，其相位包含了振动点的振动信息。微振信号的振幅M远小于发射信号波长λ。

定义初相：

(7)

和振动项：

x(τ)=Mcos(2πfvτ)

(8)

式(7)和式(8)代入式(6)后得到

(9)

在噪声条件下，式(9)改写为

An(τ)exp(jφn(τ))

(10)

式中，N(τ)为复高斯白噪声，An(τ)为复高斯白噪声的幅度，服从瑞利分布，φn(τ)为高斯白噪声的相位，服从均匀分布。

2 基于附加直流的低信噪比雷达微振动信号提取方法

2.1 基本原理

在低信噪比下，信号噪声带来较大的差分相位噪声。图2给出了式(10)代表的雷达振动信号在某τ时刻和τ+Δτ时刻的矢量表示，其中Δτ为脉冲重复时间间隔。图中，Sp为无噪声时的振动信号。在Δτ的时间间隔内，微振动信号本身的差分相位较小，不会产生相位缠绕问题。而低信噪比条件下，例如噪声水平与有用信号相当或强于有用信号时，因噪声相位服从随机均匀分布，导致差分相位缠绕，如图中所示的情况。噪声引起的相位缠绕，因其具有随机性，难以直接利用相邻差分相位之间的关系进行解缠绕。

图2 低信噪比雷达振动信号的向量表示

对噪声引起的缠绕的差分相位进行积分，反演得到的形变量存在跳变误差，破坏了振动信号信息，无法反映目标真实的形变量。

为解决低信噪比条件下差分相位的缠绕问题，本文提出附加直流方法，在原信号中附加幅度值远大于原信号幅度的直流信号K，以约束差分相位，避免相位缠绕。对式(10)表示的原信号附加直流后的信号为

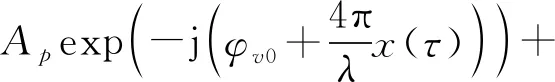
An(τ)exp(jφn(τ))+K

(11)

式中，K≫Ap，且K≫An。

附加直流后，雷达振动信号向量表示示意图如图 3所示。因附加直流量幅度远大于振动信号和噪声，则差分相位被约束，不再缠绕。

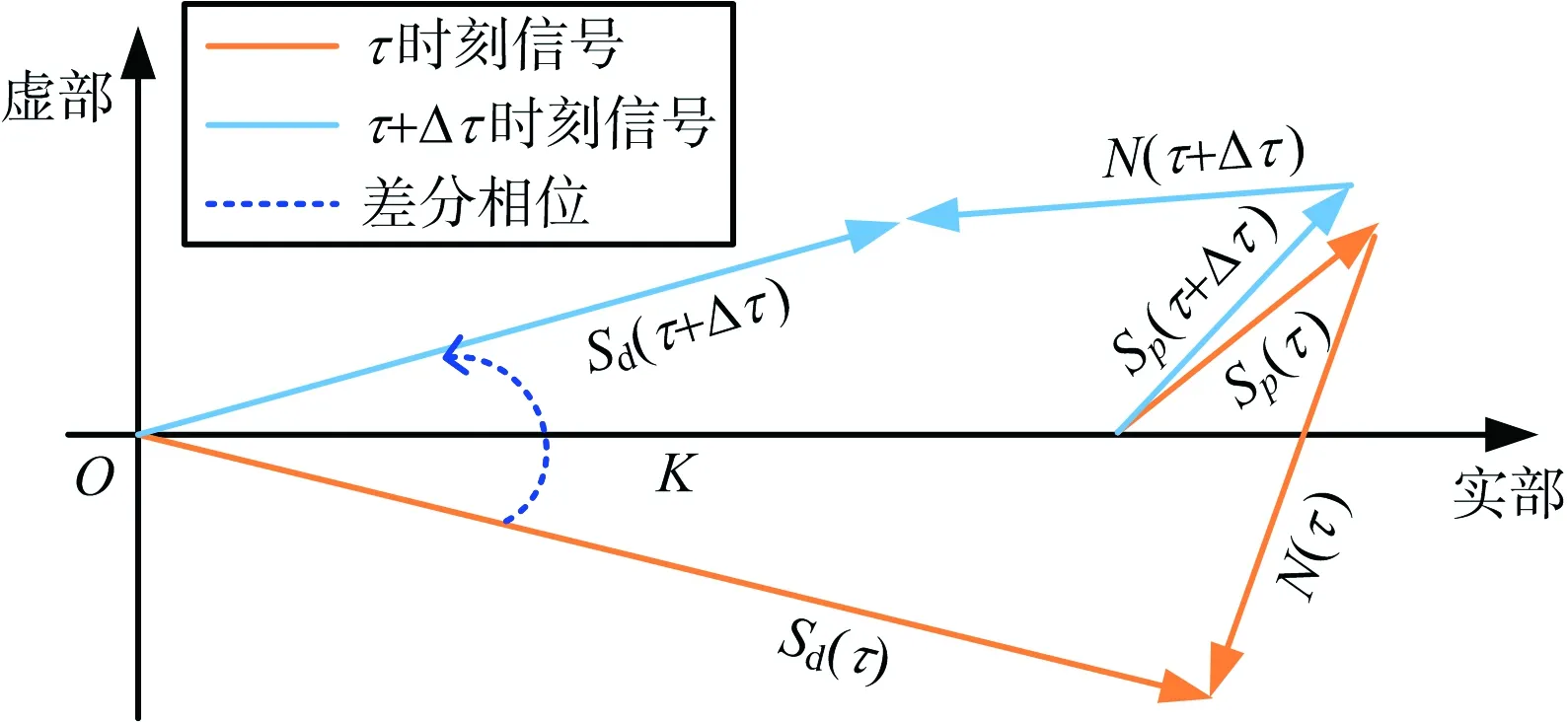
图3 附加直流雷达振动信号的向量表示

2.2 附加直流信号的相位调制系数推导

附加直流后，差分相位缠绕问题得到解决，同时，振动信号相位受到调制，附加直流后的差分相位与真实差分相位存在调制系数关系，本节将对调制系数进行推导。

在附加直流K远大于原信号幅度时，式(11)可近似为

Sd(τ)≈K·exp(jφd)

(12)

根据图 3的几何关系，相位φd近似为

(13)

式中，Ar和φr分别表示原信号Sr的幅度和相位，函数imag代表对复数取虚部。

将式(10)代入式(13)可得

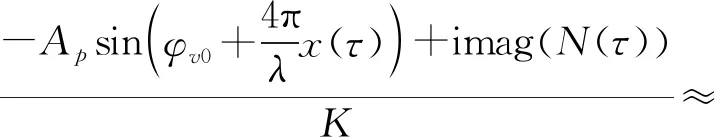
(14)

上式中采用的近似包括

(15)

以及

(16)

式(14)中右侧第一项为常数，不包含动态信息，可忽略，第二项包含了振动信息，可以看到该项对振动相位的调制系数为

(17)

在实际数据处理中求解调制系数α时，K已知，Apcosφv0可通过对原信号Sr的实部求均值得到。

式(14)中右侧第三项为复高斯白噪声的虚部，为实高斯白噪声，可通过滤波方法对噪声进行抑制。

则振动信号形变量提取的表达式为

(18)

式中，φ′d为附加直流信号的差分相位。

2.3 处理流程

基于附加直流的微振信号提取流程如图 4所示，主要步骤描述如下。

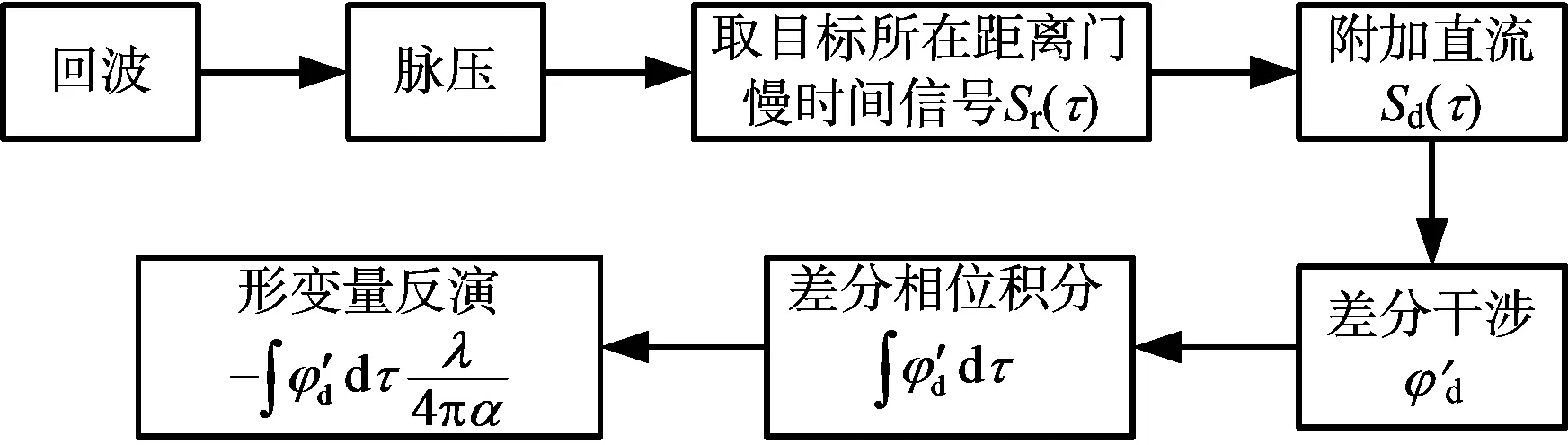
图4 附加直流法微振动信号提取流程

步骤1： 对波数据进行脉压，获得距离压缩域信号。

步骤2： 距离压缩域提取振动目标所在距离门的慢时间信号Sr(τ)。

步骤3： 对信号Sr(τ)附加直流，获得新的信号Sd(τ)。

步骤4： 对附加直流后的信号Sd(τ)进行差分干涉，提取差分相位。

步骤5： 对差分相位做积分后除以调制系数α，最后反演得到形变量。

3 仿真与实测数据分析

3.1 仿真实验

仿真参数如表1所示，表中的信噪比是指目标所在距离门的慢时间信号的信噪比，所加噪声为复高斯白噪声。

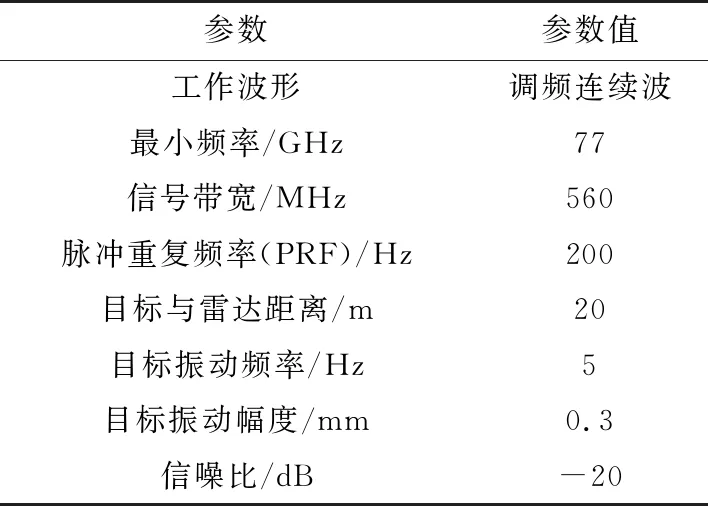
表1 仿真参数

本仿真中，将常规的直接对振动信号进行差分干涉反演形变量的方法与本文所提附加直流的形变反演方法进行比较，前者在本文中简称为直接法。

仿真结果如图5所示，图5(a)为直接法提取的形变量，可以看到跳变现象严重，形变量远远偏离真实值。图5(b)为直接法形变量的频谱，因形变量跳变，破坏了振动信息，频谱中5 Hz的振动频率分量不可见，由此可见，即使后续采用滤波方法也无法得到准确的形变量。图5(c)为附加直流法得到的形变量，未见跳变现象，因噪声水平较高，振动信息隐藏在噪声中。图5(d)为附加直流法形变量的频谱图，可以看到，通过傅里叶变换能量累积，5 Hz的目标振动频率清晰可见。图5(e)为附加直流法形变量经10 Hz低通滤波后的结果，去噪后，反演形变量与理论值接近。

3.2 定量化实验

本文采用信标仪进行定量化实验，实验场景和信标仪如图6所示。实验使用77 GHz的雷达对距离约为23 m处的信标仪进行雷达数据采集。雷达参数同表1的雷达参数，信标仪的振动频率设定为2 Hz，振动幅度为0.5 mm。

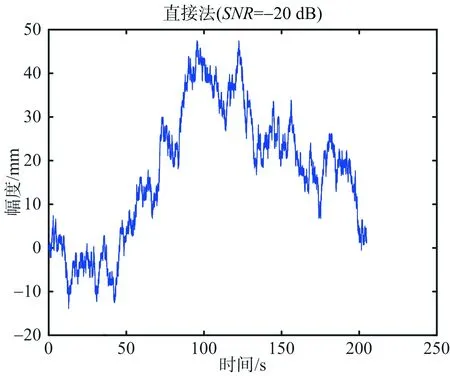
(a) 直接法提取的微振动信号形变量

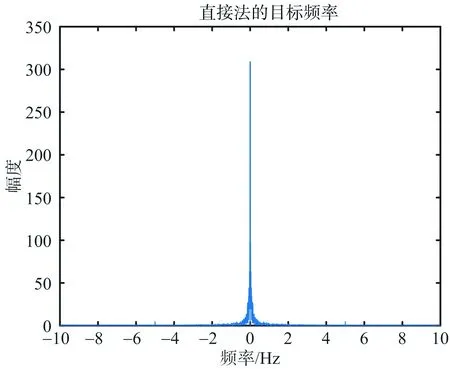
(b) 直接法形变量频谱

(c) 附加直流法提取的微振动信号形变量

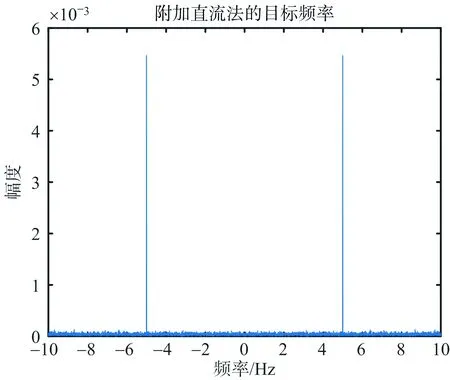
(d) 附加直流法形变量频谱

(e) 附加直流法低通滤波后形变量图5 仿真结果

图6 实验场景与信标仪照片

定量化振动实验结果如图7所示，图7(a)为某条脉冲的一维距离像，23 m处的距离峰值为信标仪所在位置。图7(b)为直接法提取的信标仪形变量，可以看到跳变现象。图7(c)为直接法形变量的频谱图，在此图中无法观测到2 Hz的频率分量。图7(d)为附加直流法信标仪形变量，无跳变现象。图7(e)为附加直流法形变量频谱图，2 Hz的频率分量清晰可见。图7(f)为附加直流法形变量经5 Hz低通滤波后的形变量。

(a) 一维距离像

(b) 直接法提取的信标仪形变量

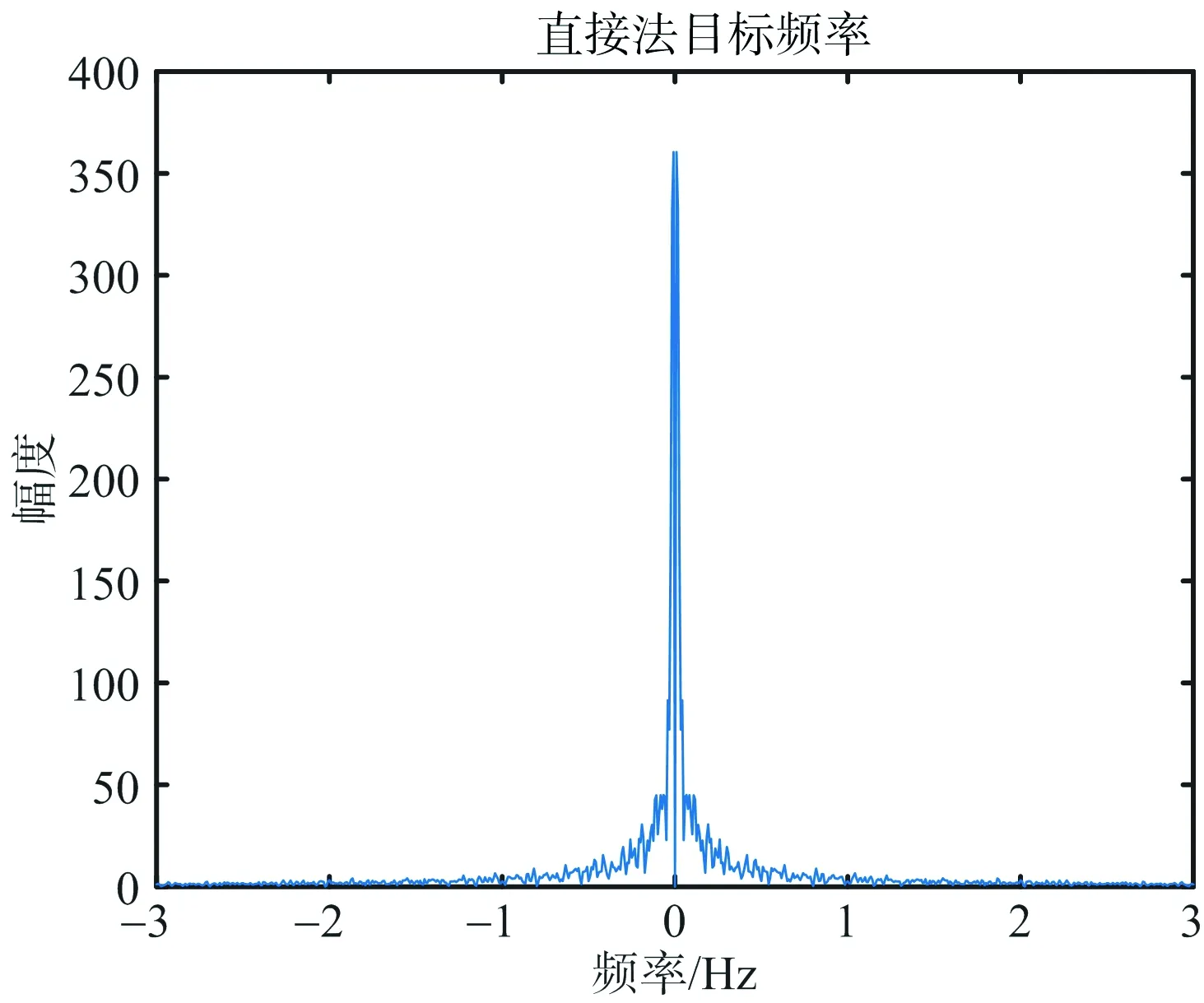
(c) 直接法信标仪形变量频谱

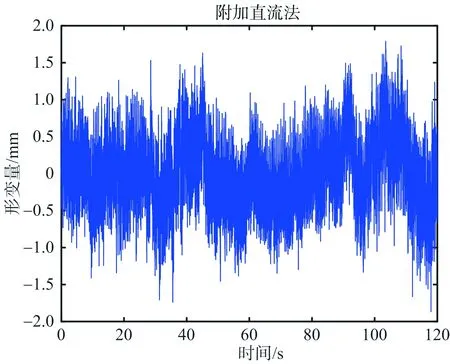
(d) 附加直流法提取的信标仪形变量

(e) 附加直流法信标仪形变量频谱

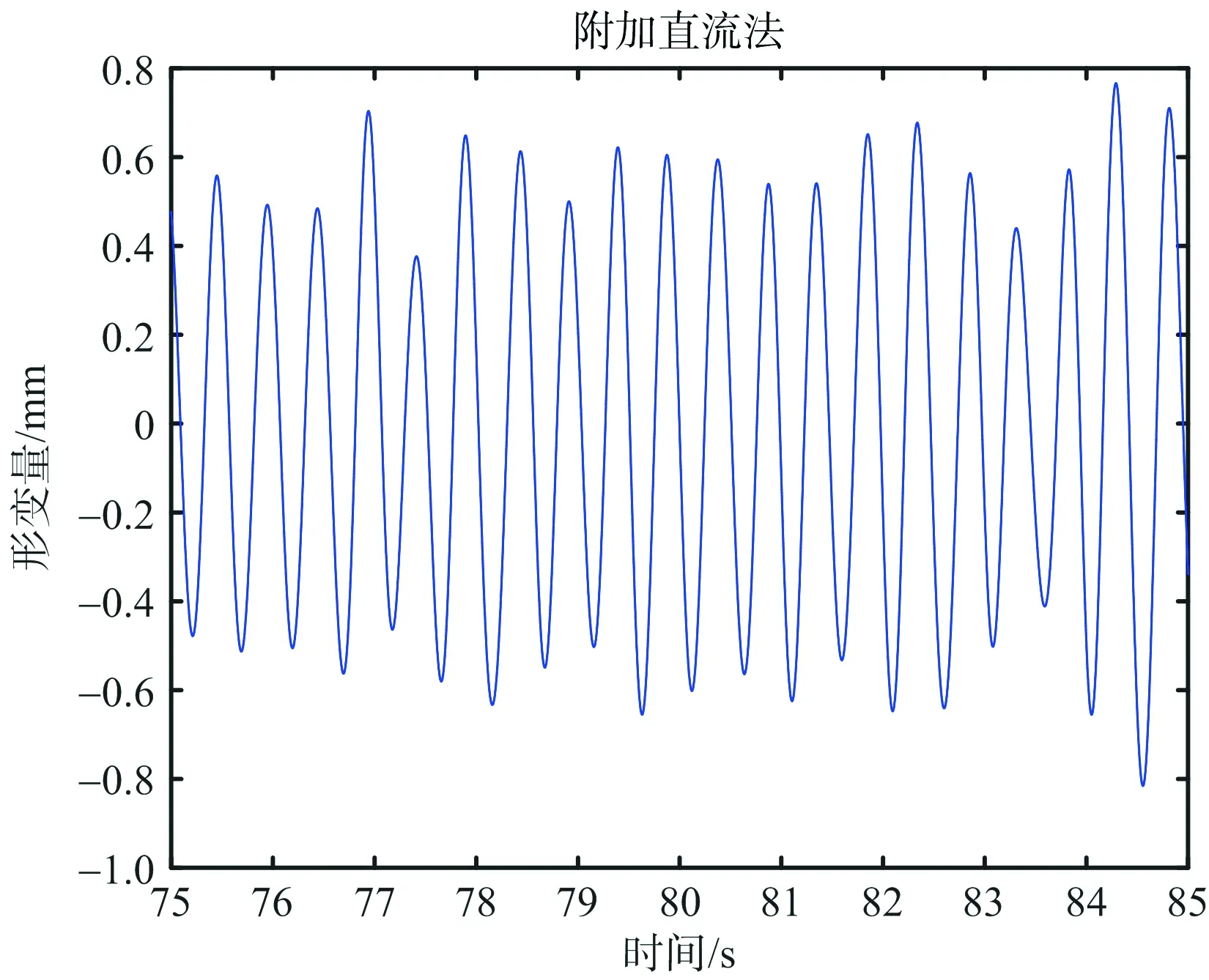
(f) 低通滤波后附加直流法信标仪形变量图7 定量化振动实验结果

上述的定量化振动实验结果分析与仿真现象一致。

3.3 桥梁实验

实测桥梁的场景如图8所示。桥梁的环境更为复杂，来往的车辆和路人等干扰都增加了桥梁监测的难度。实验采用77 GHz雷达进行数据采集，雷达系统参数设置同表 1。监测目标是桥梁拉索，目标距离雷达约17 m，观测时间为1 min。

图8 桥梁实验场景

实测桥梁实验的结果如图9所示。同前两个实验，图中分别展示了一维距离像、直接法和附加直流法各自的形变量反演结果及形变量频谱。图9(b)所示直接法形变量跳变出现在第7秒，通过同步采集的视频得知此时有行人经过，对信号产生了干扰，采用直接法无法获得准确的形变信息。图9(e)附加直流法形变量频谱显示拉索振动频率为0.5 Hz。图9(d)和图9(f)验证了附加直流法解决低信噪比差分相位的缠绕问题的有效性，能够准确提取目标的形变量。

(a) 一维距离像

(b) 直接法形变量

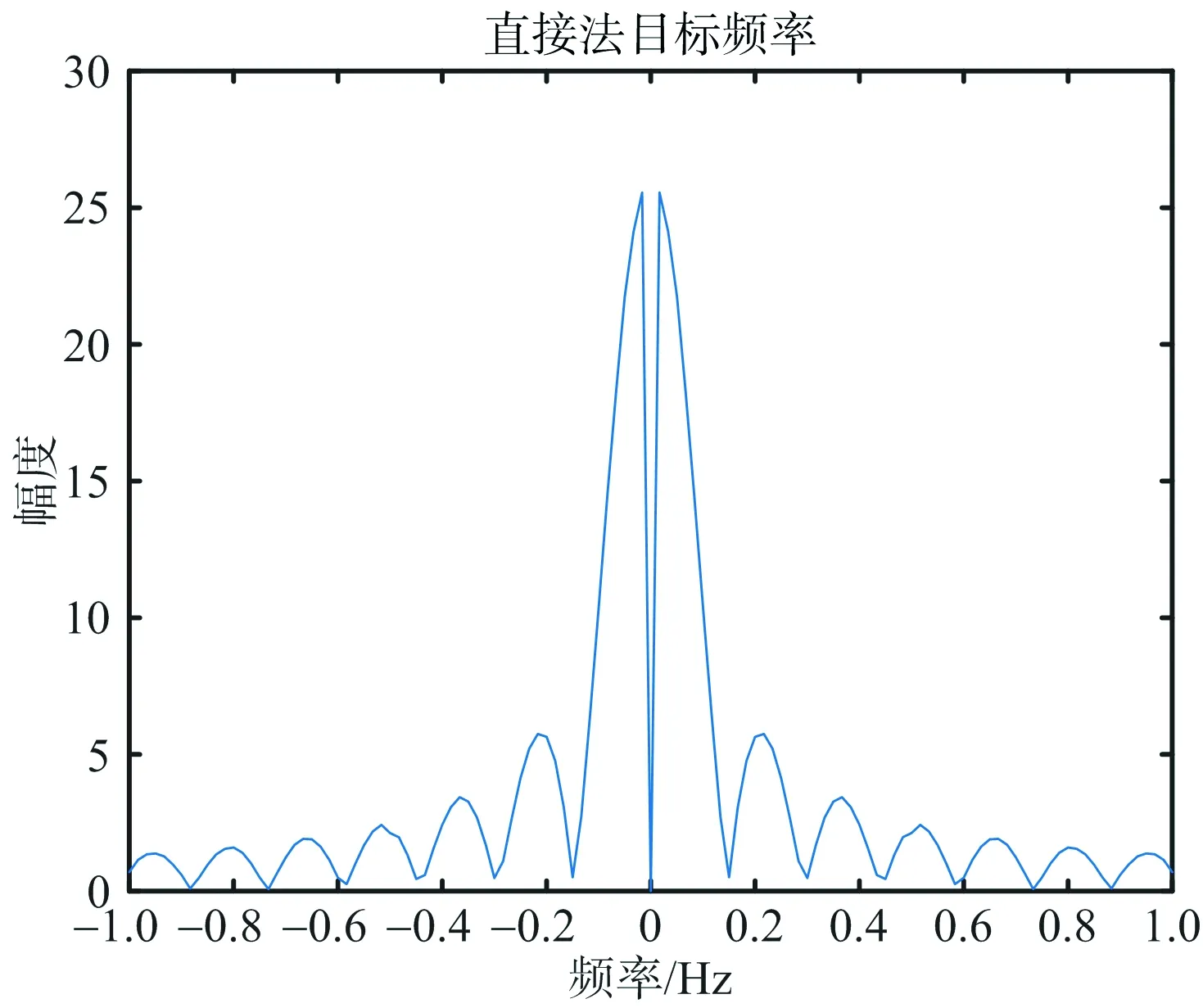
(c) 直接法形变量频谱

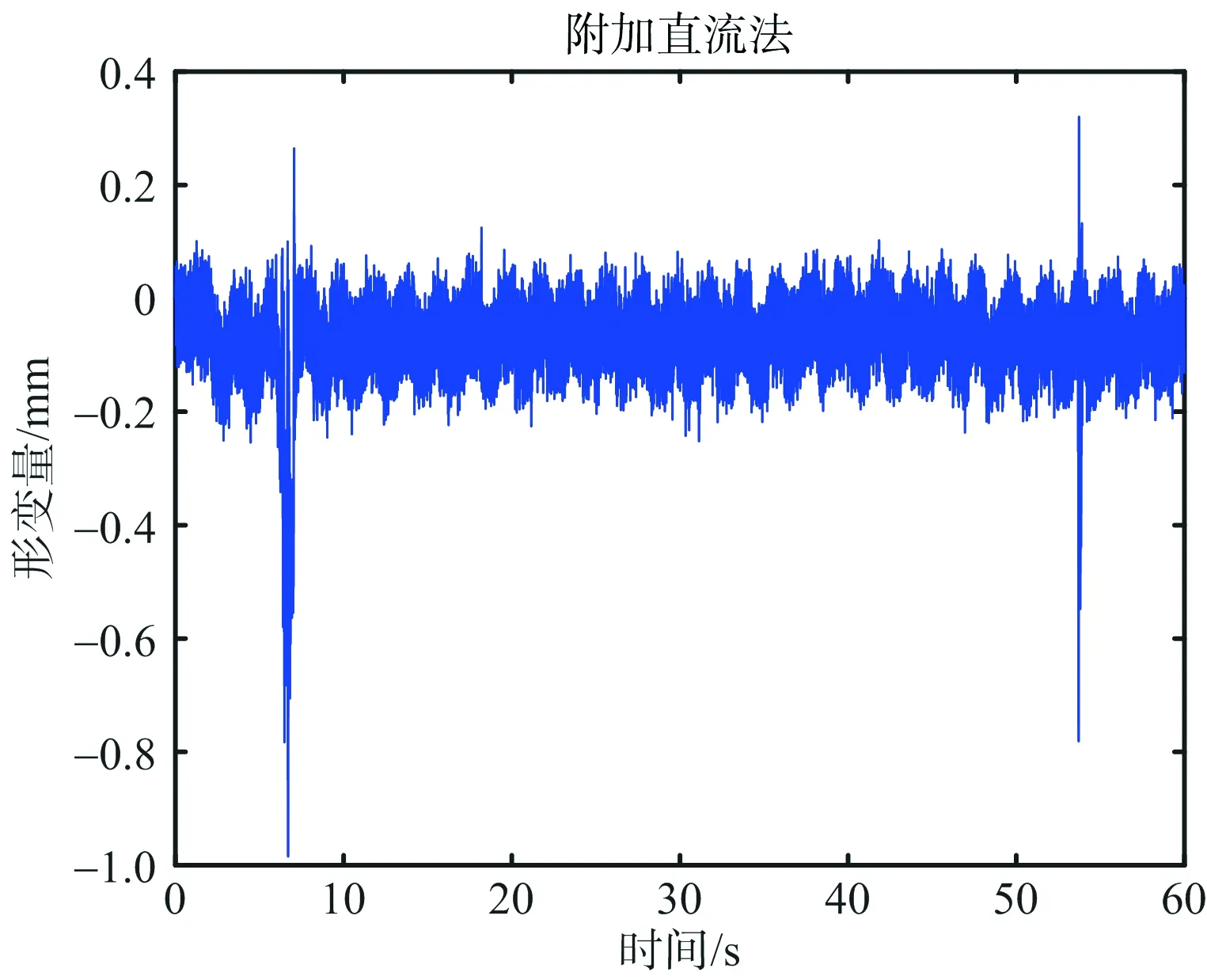
(d) 附加直流法形变量

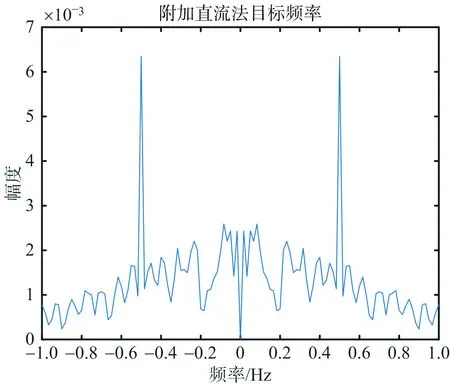
(e) 附加直流法形变量频谱

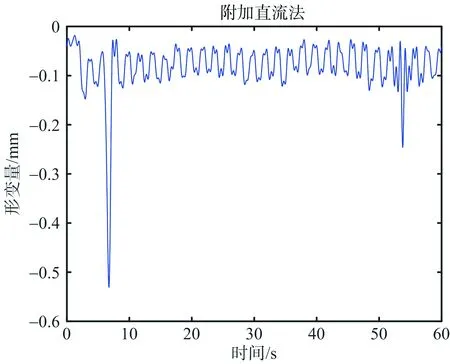
(f) 附加直流法低通滤波后形变量图9 实测桥梁实验结果图

4 结束语

利用毫米波雷达对高背景噪声下微振动目标进行形变量、振动频率等振动特征提取时，低信噪比引起雷达回波的差分干涉相位产生缠绕，导致反演形变量发生跳变，破坏了振动信息，难以获得准确的形变量和振动频率等振动信息。本文提出附加直流法解决这一问题，仅对原信号附加直流信号，就约束了差分干涉相位，避免相位缠绕。在此基础上，本文推导了附加直流带来的差分相位调制系数，可准确反演形变量。最后，仿真实验、定量化实测实验和桥梁实测实验验证了本文方法的有效性。