关于纯电动汽车的节能策略研究

谭积钻

摘 要：本文主要分析电动汽车在不同运行规律下的耗能大小，从而求出耗能最小的运行规律。其方法是：先运用拉格朗日乘子法对状态空间方程进行变分，推出目标泛函取得极值的必要条件，再通过Matlab进行求解，最后给出最优解。通过对比最优运行规律与其他几种运行规律的耗能情況，验证了最优运行规律下电动汽车的耗能最小。

关键词：最小耗能原理;节能控制;电动汽车

中图分类号：U469     文献标识码：A       文章编号：1003-5168（2021）27-0079-04

Abstract： This paper mainly analyzes the energy consumption of electric vehicles under different operation laws，and obtain a operation law with the minimum energy consumption. The method is as follows： firstly， the Lagrange multiplier method is used to variational the state space equation， and the necessary conditions for obtaining the extreme value of the objective functional are derived. Then it is solved by matlab， and finally the optimal solution is given. By comparing the energy consumption between the optimal operation law and other operation laws， it is verified that the energy consumption of electric vehicle under the optimal operation law is the lowest.

Keywords：principle of minimum energy consumption; energy saving control; electric vehicles

随着能源危机愈来愈严重，节能问题备受关注，以汽车节能作为重点研究内容逐渐成为相关领域的研究热点，并成为未来发展趋势。目前对车辆的节能研究主要分为两大类。一是系统的静态节能研究和平衡状态的节能问题，主要是改进技术结构和改善不合理的设备以提高能源利用率等。二是对系统动态的研究，即在不改进原有结构的情况下采用优化控制的方法对能量的使用进行优化处理。其中，在系统动态研究方面，主要是寻求汽车在行驶过程中的最小能耗控制规律。汽车在行驶过程中内燃机或电机的工作状态是可控的，通过给出的系统动力学方程，建立其相应的数学模型，选择合理的算法进行控制，可以得到汽车运行的最佳工作状态，从而达到节能的目的[1]。

目前在最小能耗控制系统的设计上，由于受到控制理论和数学算法的限制，主要采取简化模型的方法进行求解。将复杂非线性系统经过适当简化，给出一个线性简洁的数学模型进行等效替代。该模型需要根据行驶过程中的信息（如车速、荷载状态等）给出相应的输出转矩，控制发动机使其工作在最优工作曲线上[2，3]。

1 电动汽车的最小耗能设计思路

最速降线问题是较早的一类最优问题。该问题的提出是为了寻求在给定约束条件下使物体从起点到终点所用时间最短的最优路径。该方法是以时间最小作为指标的最优问题方法。而在现实中，除了时间指标之外，还有常被关注的指标，如能量指标。研究汽车的最小耗能控制主要内容为汽车的运行状态，本文旨在研究和探讨一种最优的运行规律，即在给定的工况下，汽车的总耗能最小[4，5]。

2 汽车的动力学方程

汽车主要由发动机系统、传动系统以及整车系统等三部分组成。以电动机作为汽车发动机，在不考虑电机达到额定电流的情况下，可以将其输出转矩视为与电流成正比，耗能大小将以电流作为性能指标的变量因素进行研究。汽车的传动系统由一系列齿轮组成，通过齿轮传动将电机的转矩输出到驱动轮，本文以单极传动为例。整车系统的动力学方程主要考虑路面牵引力、路面阻力和空气阻力。其中，牵引力依赖于驱动轮与路面的摩擦力，路面阻力取决于路面状况，空气阻力与汽车速度成正比关系[6]。

电机工作原理：电流作用于电机并使转子转动，转子带动传动轮转动将转矩输出给驱动装置，以下为电动汽车的动力学方程。

如果不考虑扭矩传递损耗，整理式（1）（2）和（3）可以得到：

以上公式中参数及其数值如表1所示。

3 状态空间方程的建立

取状态空间变量为：[x1=x]，[x2=x1]，其中，[x1]为汽车行驶的路程，[x2]为汽车行驶的速度。

根据式（4）建立状态空间方程：

4 推导最优解的必要条件

拉格朗日乘子法是一种求最优解的方法，它可以将有约束极值问题转化为无约束的极值问题进行求解，大大降低了解决最优问题的难度。它的原理是引入朗格朗日乘子将状态方程与性能指标结合起来构建哈密顿函数，之后对哈密顿函数进行变分以及微分处理，最后得出三个微分方程分别是协态方程、伴随方程和状态方程，这三个方程就统称为正则方程，而这三个方程的解将成为求解最优解的判据[7]。

取电机的耗能作为性能指标泛函：

则哈密顿函数为：

式中，[λ]为拉格朗日乘子，对式（7）进行变分和微分处理得到最小耗能的动力学控制微分方程如式（8）所示。

将约束条件以及表1中所给的参数代入式（8）求解微分方程，得到汽车最小耗能的速度表达式（9）和位移表达式（10）。

5 结果分析

利用Matlab软件将最小耗能的速度规律曲线和位移曲线绘制出来如图1和图2所示，可以看到该策略的运行规律要求汽车在25 s时间内将速度提至最大速度，随后开始缓慢减速直至停止运行。该过程严格遵守初始速度和末速度为零的约束条件，以及保证在100 s时间内运行1 000 m的位移条件[8]。

为了验证该策略的节能效用，以速度指标设计不同的运行规律进行比较，要求这些运行规律严格遵守初始速度和末速度为零的条件，以及100 s内运行1 000 m位移的约束条件。

各运行规律的速度曲线如图3所示，位移曲线如图4所示。可以看到几种运行规律均严格遵守初始速度和末速度为零的条件，以及100 s内运行1 000 m的位移条件。

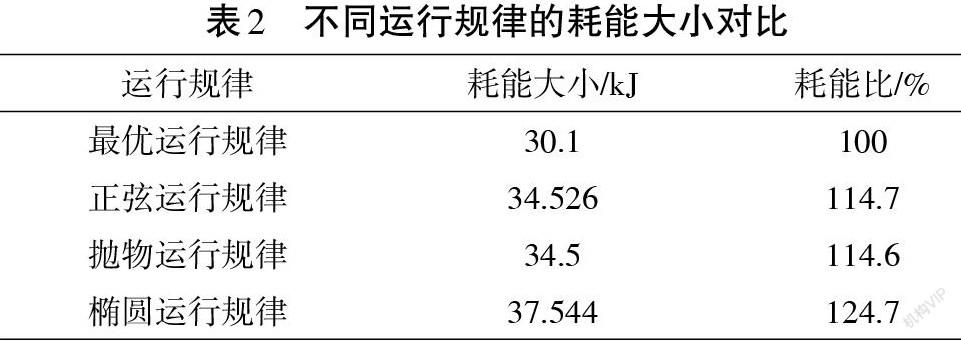
根据式（7），得到不同运行规律的能耗情况如表2所示。可以看到在相同的运行时间及运行位移的情况下，最优运行规律的能耗最小，其他运行规律与其进行比较，结果显示正弦运行规律和抛物线运行规律的耗能比最优运行规律高出14.6%，椭圆运行规律的能耗比最优运行规律高出24.7%。说明在同等条件下，运用本策略给出的运行规律具有明显的节能效果。

6 结论

本文利用最优控制理论给出了一种针对电动汽车的最小耗能控制策略，并将该策略与其他运行方案对比，结果表明运用该策略在同等工况下具有明显的节能效果。

参考文献：

[1] 胡中楫.最小能耗控制及其应用[M].杭州：浙江大学出版社，1981.

[2] 吴迪.ISG混合动力汽车能量优化管理策略研究[D].合肥：合肥工业大学，2013：1-131.

[3] 金涛涛.混合动力传动系统建模及优化控制研究[D].北京：北京交通大学，2013：1-152.

[4] 涂昊然.基于驾驶行为的纯电动汽车能耗分析方法研究[D].北京：北京理工大學，2018.

[5] 肖奡.电动乘用车节能驾驶辅助控制算法研究[D].北京：北京理工大学，2018.

[6] 杨超.电动车动力学建模与仿真研究[D].武汉：武汉理工大学，2007：1-68.

[7] 黎明安.动力学控制基础与应用[M].北京：国防工业出版社，2013：123-135.

[8] 黎明安.动力学系统建模与仿真[M].北京：国防工业出版社，2012：79-80.