用于超高移动性信道的正交时频空调制

刘梦晓 周晶 张文逸

摘要：分析了正交时频空（OTFS）调制的关键问题和研究进展，探讨了基于多载波体制的OTFS与正交频分复用（OFDM）的关系，并在超高移动性信道中仿真比较了二者的性能。數值结果表明，OTFS对信道时变引入的强多普勒效应展现了良好的稳健性，相比于OFDM能够更直接地获取分集增益。因此，OTFS有望在支持超高移动性信道可靠通信方面发挥重要作用。

关键词：OTFS；延迟-多普勒信道；OFDM；超高移动性；分集增益

Abstract： The key issues and research progress of orthogonal time frequency space （OTFS） are introduced. The relationship between multicarrier-based OTFS and orthogonal frequency division multiplexing （OFDM） is analyzed， and their performances over very high mobility channels are compared via simulation. Numerical results demonstrate that the performance of OTFS under strong Doppler effects in time-varying channels is robust， and that the diversity gain can be obtained more directly than the OFDM. Therefore， OTFS has the potential of playing an important role in achieving reliable communications under very high mobility.

Keywords： OTFS； Delay-Doppler channel； OFDM； very high mobility； diversity gain

新一代无线通信系统的愿景之一是全方位支持不同类型的通信场景和应用需求。其中，在高移动性条件下保证通信质量是一个重要方面。例如，国际电信联盟（ITU）的5G（IMT2020）愿景是支持500 km/h的超高移动性[1]。当前，中国高速铁路建设发展迅猛，人们对旅行中不间断、高质量通信的需求也在同步增长，这也凸显出超高移动性可靠通信这一课题的重要意义。

目前以第3代合作伙伴计划（3GPP）为代表的主流无线通信系统标准采用正交频分复用（OFDM）作为基础波形，能够大幅度降低宽带信道中通信发收机的实现复杂度，但在高移动性的支持能力方面面临挑战。超高移动性在时域上表现为信道响应的快速时变，这对信道估计的实时性、准确性以及导频开销控制等都造成很大压力；超高移动性在频域上表现为强多普勒效应，这导致OFDM系统出现严重的子载波间干扰，采用传统收发机体制很难应对。若简单地通过缩短OFDM符号的绝对时间长度来增强移动性支持，那么循环前缀占比将相应增大，频谱效率严重下降。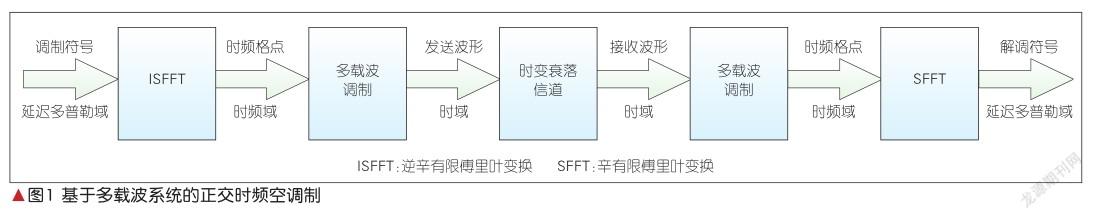

在上述背景下，近年来由R. HA？ DANI等提出的一种称为“正交时频空”（OTFS）[2-3]的新型调制技术得到了广泛关注。OTFS的主要思想是引入延迟多普勒（Delay-Doppler）域信道表示和信号调制方法，其通信过程可归结为调制符号通过延迟-多普勒域等效信道的过程。这一新思路的优越性在于能够利用无线信道的一种常见特征：即使时频域信道模型具有高时变性，其延迟-多普勒域表示通常仍是稀疏且慢变的。因此，在时变衰落信道中使用OTFS，有可能较好地控制信道估计开销和接收算法复杂度。进一步地，由于在OTFS调制过程中，每一个调制符号都经过了扩展，占据了一帧OTFS信号对应的全部时频资源，因此OTFS具有获取信道全分集增益的潜力。OTFS可通过在OFDM系统中加入预处理和后处理来实现，因此具备与主流无线通信标准的兼容性[2]。OTFS已成为近年来无线通信物理层的代表性新技术之一，受到业界的广泛关注。

本文旨在探讨基于多载波体制的OTFS技术在支持超高移动性可靠通信方面的应用前景。为此，我们在介绍OTFS基本原理的基础上，回顾了近年来对OTFS的通信性能、设计、信道估计等方面的研究进展，通过仿真研究比较了OTFS与传统的OFDM系统在超高移动性信道中的性能，说明了OTFS有望在支持超高移动性信道可靠通信方面发挥重要作用。

1 OTFS的基本原理与实现方法

对OTFS的原理可以从不同角度进行描述和解释。本文选用在通信领域最为人熟知的OTFS多载波解释，并介绍对应的实现方法。如图1所示，OTFS可视为在多载波传输基础上的一种二维扩展传输方案，可通过在OFDM系统的发、收端分别增加预处理、后处理来实现。图1中，辛有限傅里叶变换（SFFT）和辛有限傅里叶逆变换（ISFFT）[3]都是针对矩阵的二维变换，它们都可通过两次一维的快速傅里叶变换/快速傅里叶逆变换（FFT/IFFT）来实现。因此，OTFS不需要改变现行主流通信系统标准的基本波形，也不需要大幅度增加信号处理复杂度，这为其在新一代无线通信系统中的应用扫清了基本障碍。

2 OTFS的关键问题与研究进展

2.1 OTFS的滤波器设计与加窗问题

在实际信道中，物理路径通常不会准确对应延迟-多普勒平面上的格点，而成形滤波器、接收滤波器的影响也会反映到等效信道中。这些都导致OTFS延迟-多普勒域等效信道具有比公式（3）更加复杂的形式（尽管其时不变特性仍然保持），而掌握等效信道模型是在接收端实现OTFS信号检测的前提。

2.2 OTFS的信道估计与信号检测

在围绕OTFS展开的各方面研究中，信道估计是非常重要的课题。OTFS的一大优越性是，通过在延迟-多普勒域描述时频双色散信道，有可能大幅度降低信道估计的开销和复杂度。这一特性已经在若干研究中得到验证。例如，文献[8]考虑了导频与数据同传的设计方案，在延迟-多普勒域格点上设计了导频图样，通过保护间隔避免导频和数据符号之间的干扰，通过优化阈值检测信道有效路径并估计其强度，并利用估计结果检测信号。仿真结果表明，这一设计所能达到的性能与完全已知信道条件下的性能接近。在多天线系统中，OTFS的信道估计问题更具挑战性。近期已有研究者考虑大规模多输入多输出（Massive MIMO）OTFS系统的信道估计问题。例如，考虑分数阶多普勒频偏的影响，文献[9]提出了能够达到良好性能的导频设计和信道估计算法；文献[10]论证了OTFS MIMO信道的稀疏性，将下行多天线信道估计问题归结为稀疏信号重建问题，并提出了基于三维正交匹配追踪的信道估计算法，能够以较低的开销实现足够精确的信道估计。

在接收端得到对OTFS等效信道的估计后，即可实现信号的检测。由于延迟-多普勒域等效信道通常能够保持一定的稀疏性，适合应用经典的消息传递（MP）算法。文献[5]分析了OTFS等效信道的因子图模型，设计了能够同时处理非理想脉冲波形导致的时频域符号干扰以及多普勒域符号干扰的MP算法，通过仿真证明其能够在高移动性信道中实现良好的性能；所提出的MP检测器算法的复杂度仅随M和N线性增长，远低于ML检测的复杂度，具备用于实际系统的可能。但由于OTFS在多径环境下的等效因子图常具有短环结构，MP算法很容易陷入局部最优。文献[11]提出了一种变分贝叶斯迭代检测器，能够避免上述问题，保证算法收敛到近最大后验概率检测器的性能。

2.3 OTFS性能分析：分集增益与编码

OTFS通过将每一个调制符号扩展到时频二维，获取频率分集增益和时间分集增益，这与OFDM相比具有明显优势。但获取信道全分集增益仍需要一定的前提，包括信道编码和检测算法的恰当设计。文献[12]分析了OTFS系统的成对差错概率，指出在未编码情况下，其严格意义上的分集阶数仍然为1。也就是说，在信噪比足够大时，每增加10 dB的信噪比，OTFS的错误概率仅会下降一个量级。但对于实际的信噪比、错误概率范围和不太小的M和N数值，这样的效果并不会明显出现，文献[13]将这一特征描述为OTFS具有大于1的“有效分集增益”。

对编码OTFS系统分集增益的分析更具实际意义。最近，文献[14]研究了在OTFS中获取分集增益的编码设计准则，指出了在OTFS系统中编码增益和分集增益存在折中关系：分集增益随着信道可分辨多径的数量而增加，但编码增益随之减少。数值结果证明，经过恰当设计的编码OT？ FS系统在高移动性信道中能够确保获取全分集增益，而未编码OTFS系统并不具有这一特性。

2.4 OTFS用于实际无线信道

对OTFS的理论研究一般包含对时变无线信道特性的一些理想化假设，因此研究实际信道中OTFS的实现与性能具有重要意义，这方面的研究目前相对比较少。文献[15]在實测得到的毫米波车载通信信道中研究了OTFS的性能，结果表明兼顾OTFS接收机复杂度与获取分集增益并不容易，进一步优化性能需要合理选择系统参数并应用信道编码。文献[16]研究了OTFS的软件无线电实现方法，在实际的室内无线环境中研究了接收机直流偏移与载波频偏的影响，验证了该场景中OTFS相对OFDM的性能优势。

3 OTFS在超高移动性信道中的性能研究

在本节中，我们通过仿真对比不同移动速度条件下OTFS和OFDM的误码率（BER）。仿真中，我们假设OTFS的发收滤波器具有理想双正交的一些特性，并假设理想信道估计。输入符号x[ k，l]的调制方式采用四元正交幅度调制（4 QAM）。设载波频率为4 GHz，信道采用3GPP扩展车载A（EVA）模型[5]，路径数为P = 4，各径幅度增益的统计特性相同。在移动性方面，我们考虑了最高500 km/h的移动速度所导致的等效多普勒频移，体现了信道的超高移动性。

在图2（a）中，我们比较了OTFS与OFDM的BER性能，其中OFDM沿用了传统的逐符号最小欧氏距离检测器，它在无多普勒频移的信道中是最大似然检测器；OTFS则使用了MP检测器。可见，对于OFDM，随着移动性的增加，子载波间干扰相应增大，导致BER性能迅速出现错误平层。可以推断，即使借助纠错码进一步降低错误概率，也无法避免信噪比的损失。而对OTFS，仿真结果表明其性能对多普勒效应表现出良好的稳健性，这验证了其对超高移动性具有很强的支持能力。对比二者的性能，可见OTFS总能够获取更大的分集增益，而未编码OFDM系统的分集阶数为1。因此，对于一定的未编码BER，OTFS相对于OFDM具有可观的信噪比增益。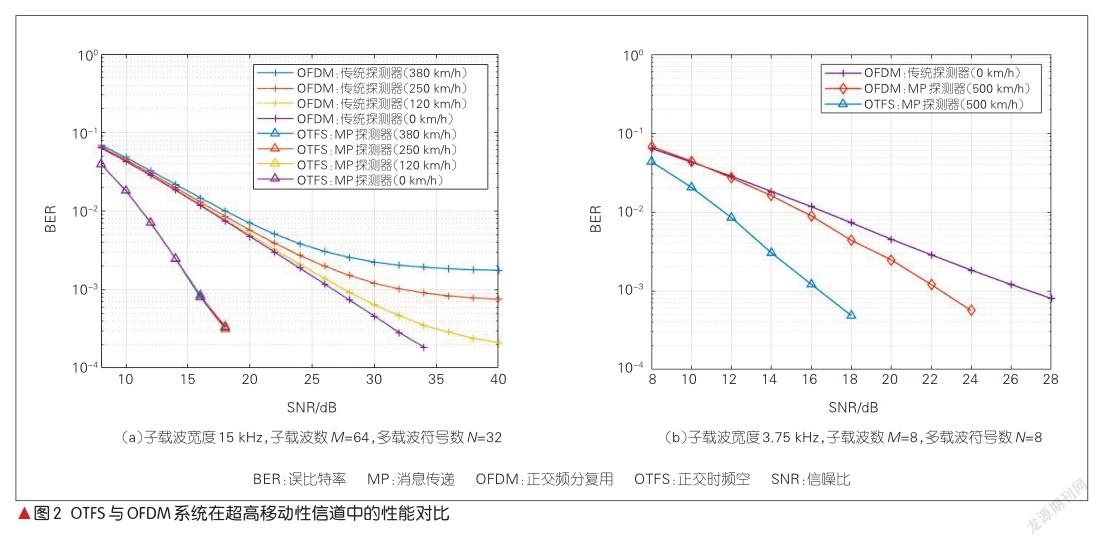

然而，OTFS的优越性与不同的比较标准和具体的系统参数设置有关。在图2（b）中，我们比较了OFDM与OTFS在均采用MP检测器时的BER性能，并改变了一些系统参数。仿真结果表明，对于OFDM，MP检测器能够在一定程度上对抗超高移动性导致的子载波间干扰的影响，其性能甚至超过了无多普勒效应时最大似然检测器所达到的性能，且表现出一定的分集增益。对此，一种合理的解释是该增益源于多普勒效应导致的符号在频域的扩展。相反，在系统参数有所改变后，OTFS的性能相对图2（a）略微变差，因此在图2（b）中相对OFDM的性能增益也就相应地减小了。如果使用了设计恰当的信道编码，那么OFDM系统所能获取的分集增益还将增加，从而使二者的性能差异进一步减小。因此，在不同条件下，OTFS的性能优越性还需要更为全面的评估，特别是需要考虑编码系统的性能。这方面的最新进展可参见文献[14]。

4結束语

新一代无线通信系统的基本波形需要灵活适配不同的通信场景。OTFS能够直接而显著地增强现有的OFDM等多载波波形体制对高移动性场景的支持能力，对全面支持高速铁路等场景、满足当前迅猛发展的通信需求具有重要意义。在基本波形的未来演进中，OTFS也有望持续发挥作用，例如有研究指出OTFS也可纳入广义频分复用（GFDM）这一新型波形体制的框架中实现[17]。

但OTFS走向应用仍然存在很多不可忽视的问题，特别是需要进一步考虑各种非理想制约因素的影响，从而明确OTFS的实际增益，避免片面夸大其作用。这些制约因素包括实际信道特性及其估计、成形滤波、编码、接收机复杂度乃至容许时延等方面。目前业界对OTFS的最终性能极限的研究仍然不够，这需要从第一性原理[18]出发，理解其性能增益的本质和关键影响因素。

致谢

感谢澳大利亚新南威尔士大学李双洋博士在文章撰写过程中给予的大力支持和帮助！

参考文献

[1] IMT-2020（5G）推进组. 5G愿景与需求白皮书[R]. 2014

[2] MONK A， HADANI R， TSATSSANIS M， et al. OTFS-orthogonal time frequency space： a novel modulation technique meeting 5G high mobility and massive MIMO challenges [EB/ OL]. （2016-08-09）[2021-06-10]. https：//arxiv.org/abs/1608.02993

[3] HADANI R， RAKIB S， TSATSANIS M， et al. Orthogonal time frequency space modulation[C]//2017 IEEE Wireless Communications and Networking Conference （WCNC）. San Francisco， CA， USA： IEEE， 2017： 1-6. DOI： 10.1109/WCNC.2017.7925924

[4] HE R S， SCHNEIDER C， AI B， et al. Propagation channels of 5G millimeter-wave vehicleto-vehicle communications： recent advances and future challenges [J]. IEEE vehicular technology magazine， 2020， 15（1）： 16-26. DOI：10.1109/MVT.2019.2928898

[5] RAVITEJA P， PHAN K T， HONG Y， et al. Interference cancellation and iterative detection for orthogonal time frequency space modulation [J]. IEEE transactions on wireless communications， 2018， 17（10）： 6501-6515. DOI： 10.1109/TWC.2018.2860011

[6] RAVITEJA P， HONG Y， VITERBO E， et al. Practical pulse-shaping waveforms for reduced-cyclic-prefix OTFS [J]. IEEE transactions on vehicular technology， 2019， 68（1）： 957-961. DOI：10.1109/TVT.2018.2878891

[7] WEI Z Q， YUAN W J， LI S Y， et al. Transmitter and receiver window designs for orthogonal timefrequency space modulation [J]. IEEE transactions on communications， 2021， 69（4）： 2207-2223. DOI： 10.1109/TCOMM.2021.3051386

[8] RAVITEJA P， PHAN K T， HONG Y. Embedded pilot-aided channel estimation for OTFS in delay-Doppler channels [J]. IEEE transactions on vehicular technology， 2019， 68（5）： 4906-4917. DOI：10.1109/TVT.2019.2906357

[9] SHI D， WANG W J， YOU L， et al. Deterministic pilot design and channel estimation for downlink massive MIMO-OTFS systems in presence of the fractional Doppler [EB/OL].（2021-05-21） [2021-06-11]. http：//arxiv. org/ abs/2015.09628v1

[10] SHEN W Q， DAI L L， AN J P， et al. Channel estimation for orthogonal time frequency space （OTFS） massive MIMO [J]. IEEE transactions on signal processing， 2019， 67（16）： 4204-4217. DOI：10.1109/TSP.2019.2919411

[11] YUAN W J， Wei Z Q， YUAN J H， et al. A simple variational Bayes detector for orthogonal time frequency space （OTFS） modulation [J]. IEEE transactions on vehicular technology，2020，69（7）：7976-7980.DOI： 10.1109/TVT.2020.2991443

[12] SURABHI G D， AUGUSTINE R M， CHOCKALINGAM A. On the diversity of uncoded OTFS modulation in doubly-dispersive channels [J]. IEEE transactions on wireless communications， 2019， 18（6）： 3049-3063. DOI： 10.1109/TWC.2019.2909205

[13] RAVITEJA P， HONG Y， VITERBO E， et al. Effective diversity of OTFS modulation [J]. IEEEwirelesscommunicationsletters， 2020，9（2）：249-253.DOI：10.1109/ LWC.2019.2951758

[14] LI S Y， YUAN J H， YUAN W J， et al. Performance analysis of coded OTFS systems over high-mobility channels [EB/OL].（2021-04-14）[2021-06-12]. http：//ieeexplore.ieee. org/document/9404861

[15] BLAZEK T， RADOVIC D. Performance evaluation of OTFS over measured V2V channels at 60 GHz [C]//2020 IEEE MTT-S International Conference on Microwaves for Intelligent Mobility （ICMIM）. Linz， Austria： IEEE， 2020： 1-4. DOI： 10.1109/ICMIM48759.2020.9298994

[16] THAJ T， VITERBO E. OTFS modem SDR implementation and experimental study of receiver impairment effects [C]//2019 IEEE International Conference on Communications Workshops（ICCWorkshops）.Shanghai， China： IEEE， 2019： 1-6. DOI： 10.1109/ICCW.2019.8757167

[17] NIMR A， CHAFII M， MATTHE M， et al. Extended GFDM framework： OTFS and GFDM comparison [C]//2018 IEEE Global CommunicationsConference（GLOBECOM）.Abu Dhabi， United Arab Emirates： IEEE， 2018： 1-6. DOI：10.1109/GLOCOM.2018.8647704

[18] MOHAMMED S K. Derivation of OTFS modulation from first principles [EB/OL]. （2021-03-1） [2021-06-11]. http：//ieeexplore. ieee. org/document/9392379

作者簡介

刘梦晓，中国科学技术大学在读硕士研究生；主要研究领域为无线通信技术。

周晶，中国科学技术大学博士后研究员；主要研究领域为信息论与通信系统。

张文逸，中国科学技术大学教授、博士生导师；主要研究领域为无线通信与网络、信息论与统计推断；主持国家自然科学基金、国家重点研发计划课题等多项科研项目。