基于摄像头和陀螺仪的四轮智能车控制方案

林振威

[摘    要]以全国大学生智能汽车竞赛为背景，介绍基于摄像头循迹的四轮智能小车控制方案，同时，在传统控制方案上增加陀螺仪反馈实现循迹控制稳定性的提升。该控制方案提供了小车对不同路段的适用性，提高了小车运行的稳定性。

[关键词]智能车;PID控制;摄像头循迹;陀螺仪

[中图分类号]TP273 [文献标志码]A [文章编号]2095–6487（2021）08–00–02

[Abstract]Taking the national college student smart car competition as the background， this paper introduces a four-wheel smart car control scheme based on camera tracking. At the same time， adding gyroscope feedback to the traditional control scheme to improve the stability of tracking control. The control scheme provides the applicability of the trolley to different road sections and improves the stability of the trolley's operation.

[Keywords]smart car; PID control; camera tracking; gyroscope

隨着科技发展，自动化和智能化的发展趋势越来越明显。而智能汽车作为今后汽车行业的一个重要发展方向[1]，近年来受到了越来越多的关注。全国大学生智能汽车竞赛则为智能汽车的发展做出了铺垫。因此，本文以智能汽车竞赛为背景，提出了一种基于摄像头和陀螺仪的智能汽车控制方案。通过摄像头采集道路信息，陀螺仪采集小车状态，单片机处理输出控制信号，实现智能循迹控制[2]。由于传统PID控制对不同赛道情况的适应能力较弱，这对小车的提速带来了困难，本方案通过在传统PID的基础上增加陀螺仪进行校正，提高了小车对不同赛道的适应能力，提升了控制系统的鲁棒性。

1 摄像头循迹

本方案采用MT9V032摄像头采集赛道信息，并通过ARM Cortex-M4内核的K66单片机进行图像处理，通过特征提取对取得偏差，对小车的转向进行控制。摄像头采集的图像为灰度图像，本文采用大津法（OTSU）二值化的方法将灰度图处理为黑白图，实现图像信息的简化，便于特征的提取。此外，本方案采用两个DMA中断交替采图、轮换处理的方式，实现了图像采集和处理的同时进行，提高了执行效率，提高了处理帧数，为控制精度的提高奠定了基础[3-4]。

将采集到的图像二值化处理后，就可以进行赛道特征的提取，本方案采用先寻找赛道两边边线，然后将两边线求和取中来拟合赛道中线，再通过求取赛道中线与图像中线的偏差的方法对小车的转向进行控制，见图1。

如图1所示，为图像处理前后的效果图，左侧为采集图，右侧为处理后的图，其中两侧是赛道边线，中间为拟合的中线。

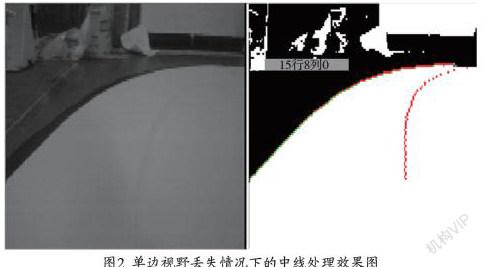
当然，小车在运行时有可能会出现视野较差，导致只能看到赛道一边的情况，对这种情况，则无法通过上述方法求取偏差，这时需要依靠一边的边线对中线进行拟合。这就需要对赛道宽度进行拟合，对于斜视图的，逆变换是一种常用的处理方法，它能够对斜视图进行处理，将其变换成“上帝视角”，然而考虑到单片机算力的限制以及摄像头视角比较固定，本方案采用了一种简化的替代方法。通过将小车正放在一条长直道的中央采图，对该图进行拟合，求出该情况下不同行高的赛道宽度，这些宽度即可近似视为该摄像头角度下采集到的图像不同行高处的赛道宽度，通过单边线加（或减）赛道宽度的一半，即可拟合出赛道中线。

如图2所示，为单边视野丢失情况下的中线处理效果图，左侧为采集图，右侧为处理后的图，其中两侧是赛道边线，中间为拟合的中线。

2 PID控制

智能车的运动是通过单片机输出不同大小的PWM波对电机和舵机进行驱动来控制的。对于不同的电机来说，其对PWM波的响应速度是有差别的。因此通过固定的PWM对电机进行控制是不可靠的，为保证小车可靠运行，保证其对响应的快速性、准确性和稳定性，采用常用的PID控制算法实现闭环控制。

PID控制作为出现最早、应用最广的控制器，以其结构简单、鲁棒性和适应性较强，调节整定很少依赖于系统的具体模型，使用简单等特点受到了广泛应用。这也是本方案采用PID控制器的一个重要原因。

PID控制器是一种线性控制器，它通过将期望值和实际值的偏差按照比例、积分、微分的线性组合得到控制量[5]，从时间的角度讲，比例作用是针对系统当前误差进行控制，积分作用则针对系统误差的历史，而微分作用则反映了系统误差的变化趋势，这三者的组合是“过去、现在、未来”的完美结合，如图3所示。

3 电机增量式PID控制

电机作为速度控制的执行机构，是小车运行时的重要控制环节。本方案采用的电机PID公式如下。

Δu（k）=u（k）-u（k-1）=KP[e（k）-e（k-1）]+KIe（k）+KD[e（k）-2e（k-1）+e（k-2）]

其中

比例P：e（k）-e（k-1）这次误差-上次误差

积分I：e（i）误差

微分D：e（k）-2e（k-1）+e（k-2）这次误差-2*上次误差+上上次误差

增量式PID根据公式可以看出，一旦确定了KP、TI、TD，只要使用前后三次测量值的偏差，即可由公式求出控制增量而得出的控制量Δu（k）对应的是近几次位置误差的增量，而不是对应与实际位置的偏差，没有误差累加。

也就是说，增量式PID中不需要累加。控制增量Δu（k）的确定仅与最近3次的采样值有关，容易通过加权处理获得比较好的控制效果，并且在系统发生问题时，增量式不会严重影响系统的工作。

此外，增量式PID控制输出的是控制量增量，并无积分作用，因此该方法适用于执行机构带积分部件的对象，如步进电机等，而位置式PID适用于执行机构不带积分部件的对象，如电液伺服阀。

在进行PID控制时，位置式PID需要有积分限幅和输出限幅，而增量式PID只需输出限幅。因此对于电机的控制，选用的是增量式PID控制。

4 舵机位置式PID控制

舵机作为转向的执行机构，需要较快的响应速度，因此对舵机采用了位置式PID控制。公式如下

其中：+

比例P：e（k）

积分I：∑e（i）误差的累加

微分D：e（k）-e（k-1）这次误差-上次误差

也就是位置式PID是当前系统的实际位置，与你想要达到的预期位置的偏差，进行PID控制。

因为有误差积分∑e（i），一直累加，也就是当前的输出u（k）与过去的所有状态都有关系，用到了误差的累加值（误差e会有误差累加），输出的u（k）对应的是执行机构的实际位置，一旦控制输出出错（控制对象的当前的状态值出现问题），u（k）的大幅变化会引起系统的大幅变化。

并且位置式PID在积分项达到饱和时，误差仍然会在积分作用下继续累积，一旦误差开始反向变化，系统需要一定时间从饱和区退出，所以在u（k）达到最大和最小时，要停止积分作用，并且要有积分限幅和输出限幅。

所以在使用位置式PID时，一般直接使用PD控制。

而位置式PID适用于执行机构不带积分部件的对象，如舵机和平衡小车的直立。

5 加入陀螺仪的循迹控制方案

由于小车需要适应不同类型的赛道，这对PID参数的适用性和整个控制系统的鲁棒性提出了较高的要求。尤其是在小车高速运行的情况下，很难同时兼顾不同类型的道路。

针对这个问题，采用动态参数对PID进行控制，针对计算出的不同偏差值，给定一个与偏差相关的PID参数，这样即解决了一套参数对不同赛道适应能力不一致的情况。但是，简单的动态参数的控制效果仍然有限。因此，本方案在以上控制策略的基础上加入了陀螺仪。

陀螺仪是一种角速度测量传感器，本方案通过测量小车运行时的横向角速度，即可判断出小车当前运行的状态。若小车在直道上左右来回摇摆，会产生一个来回振荡的横向角速度，通过测量该角速度，并通过在PID输出的基础上减去（或加上）一定比例的该时刻的角速度值（本文称其为阻尼项），即可抑制小车的振荡。控制框图如图4。

对应公式如下：

u（k）=Kpe（k）+Kd[e（k）-e（k-1）-Kkω]

其中ω为角速度，Kk为对应系数。

阻尼项的作用在于减缓小车在转向时的响应幅度，减小其在转向时产生的超调量，起到抑制大超调量，消减小幅高频振荡的作用，以通过小车运行时的稳定性。

6 结束语

智能化、自动化是汽车行业未来发展的一个重要方向，智能小车的研究则是对智能汽车行业的一种简单探索，本文阐述的控制思路仅是众多控制方案的一种，这其中还有许多的东西值得去研究和探索。

参考文献

[1] 《中国公路学报》编辑部.中国汽车工程学术研究综述·2017[J].中國公路学报，2017，30（6）：1-197.

[2] 王盼宝，佟超，曹楠，等.智能车制作[M].北京：清华大学出版社，2001.

[3] 张铮，范若怡，宫若宁，等.基于图像处理的智能小车无线远程灭火[J].实验室研究与探索，2018，37（1）：33-37.

[4] 孙晓峰.基于图像识别的智能小车障碍物检测方法研究[D].昆明：昆明理工大学，2017.

[5] 丁鹏.自寻迹智能车PID控制研究[D].衡阳：南华大学，2018.