考虑工位优先级的智能车间双向物料配送路径规划*
2021-11-27童傅娇张守京
童傅娇,徐 进,张守京
(西安工程大学 机电工程学院,陕西 西安 710048)
0 引 言
车间物料配送路径优化问题是指在一定条件约束下,按照工位物料需求规划小车的配送路径,使其按照规划路径进行物料配送,并达到一定的优化目标。随着互联网与传统产业的融合发展,机械车间高度灵活的个性化和数字化的产品与服务的生产模式已逐渐取代传统生产模式。生产模式的不断变化,在一定程度上使得机械车间环境更为复杂,生产物流的流畅性难以保证。同时,由于机械车间内各类不确定问题频繁发生,物料配送方案对实际工况的适应程度大大降低[1,2]。针对上述问题,国内外学者对该问题的各类影响因素进行了大量的研究。
如在准时制配送方面,不少学者考虑了以配送时间窗为约束[3],如采用混合时间窗[4]、模糊软时间窗[5]、正态模糊隶属度[6]等来表示工位的满意度。在不确定因素方面,蒋增强等人[7]针对不确定环境下的物料配送问题设计了动态周期的物料配送策略。ALNAHHAL M等人[8]考虑机器故障、停线、产品报废等生产线不确定因素,提出了一种动态配送策略。李思国等人[9]对离散制造车间的实时物料配送路径进行了优化。在多目标优化方面,刘爱军等人[10]考虑到柔性车间中存在的动态多目标问题,提出了基于事件驱动和循环驱动的混合重调度策略。夏扬坤等人[11]以配送总成本和小车数量为优化目标,建立了求解配送路径规划问题的数学模型。WANG H F等人[12]以总成本最小和车辆数最少为目标,通过建立相应模型进行了求解。在对车间物料循环配送、回收方面,周蓉等人[13]提出了车辆装卸一体化路径问题。张守京等人[14]在分析车间物料循环的基础上,提出了一种车间物料配送与余废料回收协同的路径优化方法。在求解算法方面,多以群智能算法为主,局部邻域搜索算法使用较少。BANOS R等人[15]在车辆行驶路径长度和车辆负载两个方面进行了综合权衡,以构建问题模型,并采用改进的多目标遗传算法对模型进行了求解。孙宝凤等人[16]针对动态取送路径下的各种实时信息传递对问题的作用和影响,设计了禁忌搜索算法以对模型进行求解。LI Guang-qiang等人[17]提出了通过改进的AFSA对路径规划问题进行求解,并验证了算法的有效性。
通过对上述文献的研究及对机械车间现状的分析基础上,笔者总结出目前机械车间物料配送仍存在以下问题:
(1)配送时间未满足工位需求时间要求,工位服务满意度较低;
(2)物料配送多以单向需求配送为主,未考虑将回收与需求协同规划;
(3)当出现紧急订单、催单、撤单等现象时,未考虑按照工位物料需求紧急度,对工位进行配送。
针对上述问题,笔者提出一种考虑工位优先级的车间双向物料配送策略,同时以物料配送总成本最小为优化目标建立数学模型,并借用遗传禁忌搜索混合算法对问题进行求解,最后通过仿真实验证明混合算法的有效性。
1 问题描述与模型建立
1.1 问题描述
考虑工位优先级及车间双向物料配送路径优化问题是指在满足自动引导小车(automatic guided vehicle,AGV)装载量、时间窗约束等限制条件下,车间物料配送在考虑工位优先级及车间双向物料配送情况下实现AGV配送路径最优、工位满意度最高及总成本最低。其中,工位优先级是指当出现生产扰动如紧急订单、催单、撤单等现象时,工位之间对物料的需求紧急程度不一,服务紧急订单和催单的工位对物料的需求更为迫切,因此需要先对这些工位进行配送。而对于撤单的工位,可以延后对这些工位的物料配送。上述生产扰动对工位物料配送紧急程度造成一定影响,即对工位配送时间有更急迫或缓和的需求。因此,笔者以工位最佳配送时间作为工位配送优先级的参数,工位最佳配送时间越小则工位优先级更高;车间双向物料配送是指在给工位配送物料时,同时将工位的成品进行转运和余废料的回收,形成双向物料流的物料配送模式。
考虑工位优先级及车间双向物料配送的配送策略示意图如图1所示。

图1 配送策略示意图
配送小车装载工位需求的物料从配送中心出发对工位进行服务,工位上的数字代表小车服务顺序,该顺序按照工位优先级进行排序,在对各工位进行配送服务的同时,以“先卸后装”的方式将工位产生的成品及余废料转运与回收。
其问题约束如下:
(1)加工车间内只有一个配送中心0,且小车的起止点均为配送中心;
(2)配送小车k均相同,小车最大载重Q、最大路程等信息已知,车辆数量K能满足所有客户点需求。小车行驶速度v恒定;
(3)小车按照“先配送后回收”的顺序对N个工位进行服务,即对于既有物料需求,又有成品转运或余废料回收的双向需求工位,按照先物料卸载,后成品转运或余废料回收的装载顺序进行服务;而对于只有物料需求或成品装运、余废料回收的单向需求工位,直接进行服务。上述任务均需满足小车容量限制;
(4)车间内工位物料需求信息、工位优先级、配送中心与工位坐标均已知,配送路径中所有节点可互相连通;
(5)工位配送满足时间窗约束,违反时间窗约束则设置惩罚。
1.2 模型建立
根据以上论述,考虑工位优先级及车间双向物料配送路径优化模型表示如下:
(1)
(2)
(3)
pi+si≤qi,∀i∈N;
(4)
(5)
x0ik=xi0k,∀i∈N,∀k∈K;
(6)
(7)
(8)
xijk、xik、yik∈{0,1}.
(9)
式中:C—总配送成本;qi—工位i的物料需求量;pi—工位i的成品转运量;si—工位i的余废料回收量;dij—工位i与j之间的曼哈顿距离;d0i—配送中心到工位i的距离;ci—工位i的时间窗惩罚成本;t—小车到达工位时间;RTi—工位i可接受的最早配送时间;LTi—工位i可接受的最晚配送时间;Ii,Ij—工位i,j的优先级参数;u—车辆单次派遣成本;λ—每千米运输成本;α—物料早到工位的惩罚因子;β—物料晚到工位的惩罚因子;i,j—工位编号;x,y—关联系数。
模型中,目标函数式(1)表示AGV配送总成本最小,其中包括AGV派遣成本,配送距离成本,时间窗惩罚成本;约束式(2)表示每辆小车的装载容量不能超过小车最大装载量;约束式(3)表示每个工位只被服务1次且仅有1辆小车执行任务;约束式(4)表示任一工位的回收量及转运量不超过该工位的需求量;约束式(5)表示到达工位和离开工位的小车相同;约束式(6)表示所有车辆均从原配送中心出发并最终全部返回原配送中心;约束式(7)表示小车按照工位的优先级进行配送,对于任意工位i与j,若工位i的优先级大于工位j,即工位i的最佳配送时间小于工位j时,优先执行工位i的任务;约束式(8)为时间窗约束,物料在时间窗外送达工位将进行惩罚;约束式(9)为决策变量属性。
2 模型求解
遗传算法(genetic algorithm,GA)在解决物料配送路径优化问题具有一定优势[18,19],虽然目前禁忌搜索算法(tabu search algorithm,TSA)在解决物料配送路径优化问题中使用较少,但TSA在该类型问题表现的有效性已被许多研究证明[20,21]。因此,笔者在已有的研究基础上,采用遗传禁忌混合算法(genetic taboo hybrid algorithm,GTHA)对所述模型进行求解,具体求解过程如下。
2.1 遗传算法设计
针对本文出现的配送车辆容量约束问题,物料配送无法一次完成,而需要多车辆同时配送的情况,编码需要更直观地体现各车辆的配送路径,所以笔者采用自然数编码。染色体编码结构如下:
0,Ni1,Ni2,...,Nio,0,Nj1,Nj2,...,Njp,0,Nk1,Nk2,...,Nkq,0...
其中:Nkq—第k辆车的第q个配送任务是为工位点Nkq进行物料配送及回收;0—配送中心。
由3辆车对工位进行物料配送的染色体编码示意图如图2所示。
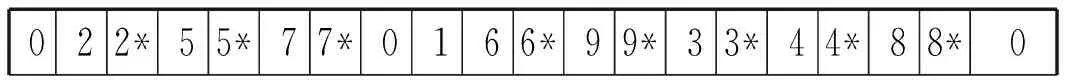
022*55*77*0166*99*33*44*88*0
图2中带有*号的工位表示该工位有成品转运或物料回收需求,则小车1的配送路径为0-2-2*-5-5*-7-7*-0,小车2的配送路径为0-1-6-6*-9-9*-3-3*-0,小车3的配送路径为0-4-4*-8-8*-0。
2.1.1 确定初始种群
采用随机生成100条染色体的方式确定初始种群,初始种群中编号为[1~N],由于存在装载容量的约束,需对初始种群中的每条染色体所包含的工位进行车辆分配,以确定每条路径所包含的工位。初始种群染色体车辆分配步骤如下:
(1)随机选取100条染色体中的一条染色体个体;
(2)首先对该染色体所包含的工位按照工位优先级进行排序,即每个小车优先配送优先级高的工位;
(3)然后按照车辆的装载能力将染色体上的工位分配给小车,达到小车的装载能力后,将剩下的工位分别给另一辆小车。以此方式,完成该染色体上的工位分配;
(4)重复上述操作,直到达到初始种群规模。
2.1.2 适应度函数
以总成本的倒数作为适应度函数的评价值,表示为成本越低的种群个体适应度越好:
(10)
2.1.3 选择操作
选择操作是将精英保留策略与轮盘赌选择相互结合。首先保留适应度最大的个体,即精英个体,剩余个体采用轮盘赌法进行筛选。
2.1.4 交叉操作
笔者选择部分匹配交叉算子,以概率Pc选择个体。交叉操作示意图如图3所示。
2.1.5 变异操作
笔者选择交换变异法进行变异操作,以变异概率Pm选择个体。变异操作示意图如图4所示。

图3 交叉操作示意图

图4 变异操作示意图
遗传算法具有较强的全局搜索特性,但易提前收敛,结合TSA算法较强的局部搜索特性,笔者在遗传算法逐渐收敛时引入禁忌搜索算法,对求解结果进行二次优化。
2.2 禁忌搜索算法设计
禁忌搜索算法的思想为:
(1)以遗传算法收敛时的求解结果作为禁忌搜索算法的初始解,通过遍历所有工位,将工位从当前路径移除,然后依次插入到其他路径的可行位置中构造邻域解,最后以总成本最低选择最优解;
(2)建立禁忌表记录和选择优化流程,该禁忌表不仅可以防止禁忌搜索算法陷入局部优化,而且指明了下一步搜索方向。
遗传算法由于其群智能算法特性易陷入局部最优,当算法求解逐渐收敛时插入禁忌搜索算法可避免这一状况,从而获得更优解。禁忌搜索算法二次优化求解结果实现步骤如下:
(1)根据遗传算法当前产生所有个体,建立禁忌搜索集合NS;
(2)选择集合NS中某个个体ti,置空禁忌表并设置最优状态为空;
(3)由选择的ti构造领域解,并确定其候选解;
(4)禁忌处理和特赦操作。当出现一个解的目标值优于之前任何一个最佳候选解时,进行特赦操作,然后将该解作为当前最优解,并放入禁忌表中。若不存在此解,则从所有邻域解中选择非约束最优解作为特赦,同时将其放入禁忌表中,并释放满足禁忌步长T的对象;
(5)如果对ti的搜索达到最大迭代次数,则结束对ti的搜索,并转到后一步。否则转到第3步。
(6)如果NS中所有对象均以完成禁忌搜索操作,则输出优化结果。否则跳转至禁忌搜索第2步。
2.3 遗传禁忌搜索混合算法流程图
GTHA流程图如图5所示。

图5 GTHA流程图
3 实例验证与分析
3.1 实验设置
针对本文研究问题,笔者采用文献[22]中的原始实例进行验证,并按照本文研究问题特点,对原始数据进行适当调整。
某电动车机械零件加工车间示意图如图6所示。

图6 车间生产示意图
该车间拥有5条生产线,在某一时段,车间有45个工位需要物料的配送或余废料回收服务。车间下方包括配送中心及物料仓库,在进行物料配送及回收服务时,AGV从配送中心0出发,在对所有需求工位进行服务过后,将转运的成品及回收的余废料送至物料仓库0’后最终返回配送中心。在实验中,以物料最佳配送时间作为工位优先级的参数,最佳配送时间越小,表示工位优先级越高。为了使计算更贴切现实生产车间,工位之间的距离计算采用曼哈顿距离计算方法。本文采用Matlab2016b对实例进行验证,相关参数设置为:Q=1 000单位,v=5 000 m/h,u=250元/次,λ=1.5元/km,α=60,β=900;GA种群规模n=100,Pc=0.9,Pm=0.08,最大迭代次数C=500;TSA最大迭代次数I=500,禁忌步长T=20。
车间内配送中心、物料仓库及工位信息表如表1所示。
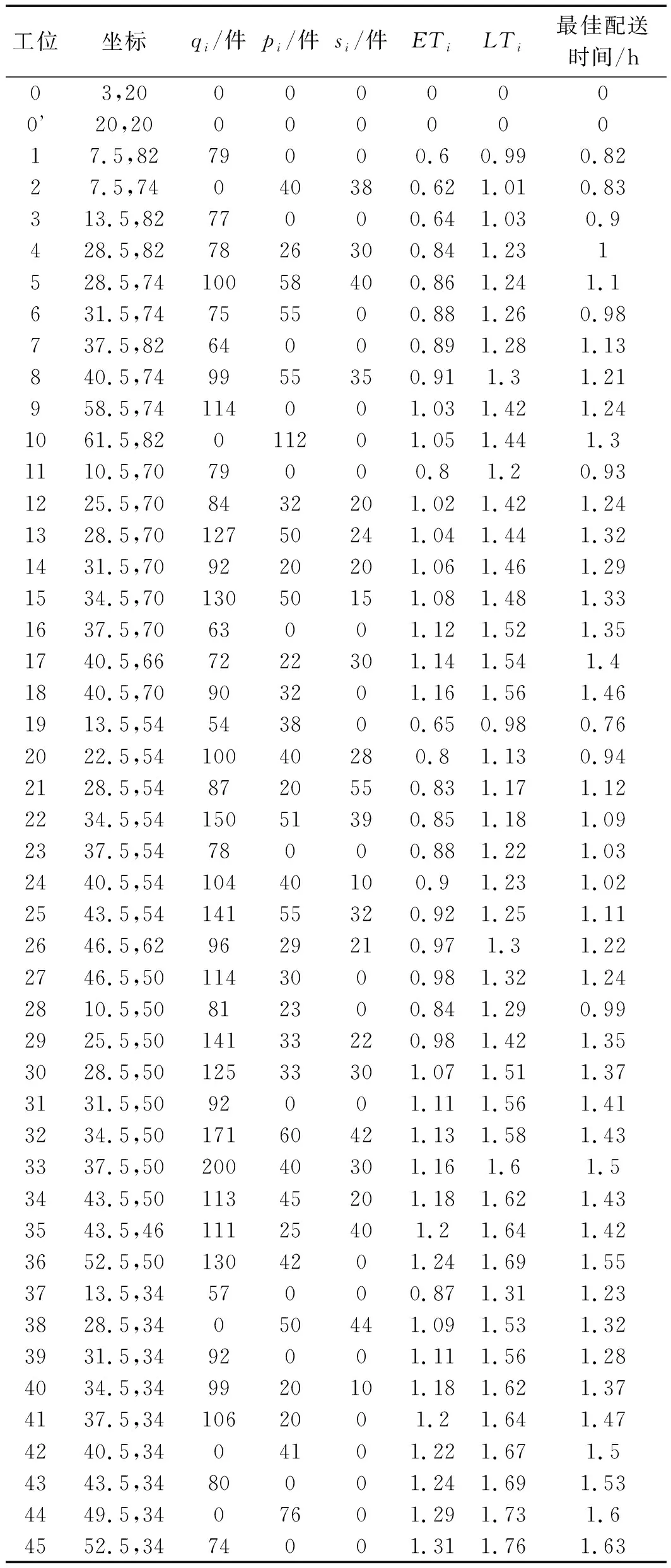
表1 配送中心、物料仓库及工位信息表
3.2 结果对比与分析
为使求解结果不失一般性,笔者用GTHA随机求解20次,取20次平均结果,平均总成本为5 158.1元,工位优先服务率为61%;以同种情况下仅用遗传算法进行求解,取20次平均结果,平均总成本为5 546.6元,工位优先服务率为65%。遗传算法收敛曲线如图7所示。
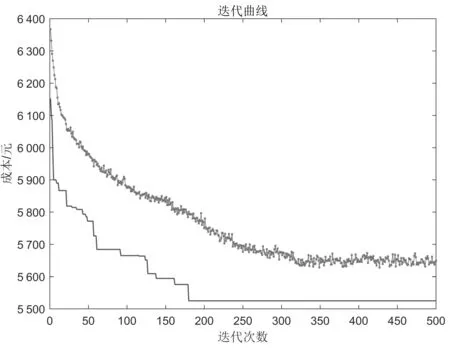
图7 遗传算法收敛曲线
由图7可知,遗传算法在20次仿真中,平均200代开始收敛,图中上下两条收敛曲线分别代表各代平均成本和最小成本。GTHA混合算法收敛曲线如图8所示。
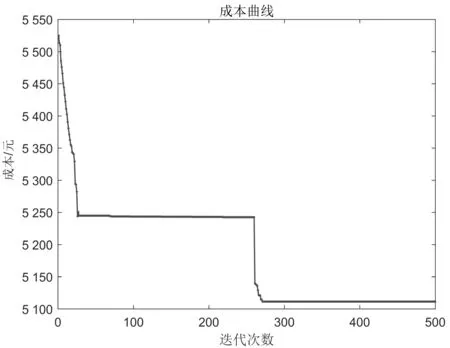
图8 混合算法收敛曲线
由图8可知,GTHA有两次收敛现象,第一次收敛平均在第20代,第二次平均收敛在第250代,图中迭代曲线表示各代最小成本曲线。
在20次实验中,遗传算法与GTHA求解结果即成本对比图如图9所示。
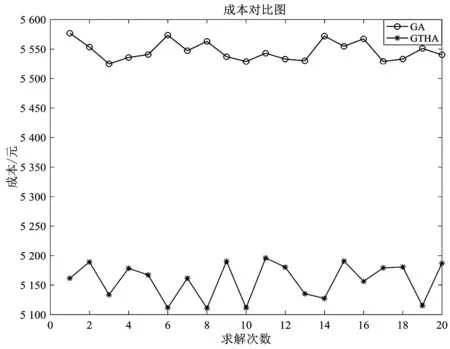
图9 成本对比图
由图9可知,GTHA求解的结果均优于仅使用遗传算法求解的结果,证明了混合算法的优良性。
取20次实验中的一次,其求解结果汇总表如表2所示。

表2 求解结果汇总表
由表2结果可知,利用GTHA及仅使用遗传算法求解结果均为5辆小车进行服务,但使用GTHA比仅使用遗传算法成本降低了399.5元,且工位优先服务率提高了3%。
上述求解结果表明了考虑工位优先级的车间双向物料配送策略在复杂生产车间应用的有效性,也验证了混合算法的优良性。
4 结束语
针对日益复杂环境下机械生产车间工位物料需求响应慢、运输小车利用率低等问题,笔者提出了考虑工位优先级的车间双向物料配送策略并建立相应优化模型,采用遗传禁忌搜索混合算法对优化模型求解,并利用MATLAB对实例进行了仿真验证。
研究结果表明:
(1)通过约束工位优先级,满足了对工位物料需求紧急程度的及时响应;车间内双向物料配送模式,提升了配送小车的利用率,同时实现了对工位产生的成品转运及余废料及时回收;
(2)以总配送成本最低建立目标模型,采用遗传禁忌搜索混合算法对优化模型进行了求解。与仅使用遗传算法对比,混合算法分别使成本降低了399.5元,工位优先服务率提高了3%,证明了混合算法的优良性。
为了更进一步适应日益复杂的机械车间生产环境,未来笔者将研究动态物料需求及不同物料类型下的车间物料配送路径规划问题。
