薄壁旋转碟片的耦合热应力分析
2021-11-27张翠张坤
张翠 张坤
上海杉达学院机械工程学院,中国·上海 201209
1 引言
现代工业追求高功率化的趋势势必导致工业构件处于更复杂的工作环境中,典型的包括机械加工中磨削砂轮和电机中的转子等均受到极强的惯性力和温度载荷。这些工业构件均属于薄壁旋转碟盘类模型,该模型的失效是机器整体中最常见、最高发的,其中内径高副配合处应力集中环带的应力强度又是该模型失效的主要诱因之一[1]。
2 数学模型
均质等厚度薄壁旋转碟片不受外力作用,而仅受到由于碟片绕中心轴z旋转导致的平行于碟片板面的惯性力作用时,旋转碟片可简化为平面应力情况下的同心圆数学模型,以其圆心为参考极坐标系原点O,其内、外径位置分别为a,b,记径向位置及极角分别为r、θ,且碟片转速为ω。
3 力学模型
薄壁旋转碟片模型的几何形状和所受外力均不随极角θ变化,这类问题中模型结构和受力情况均对称于中心轴z,因而其应力只与径向位置r有关,与极角θ无关。故论文模型属于应力轴对称问题[2],该平衡微分方程为:
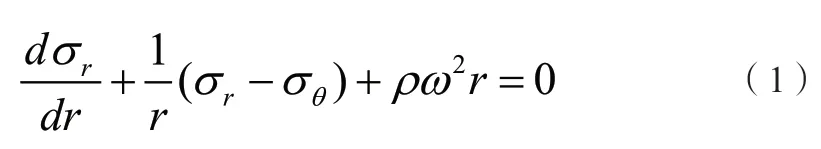
式中:σθ为环向应力,rρω2项是碟片旋转导致的惯性力,其中ρ为单质材料密度,由于其为径向位置r的函数,所以这是一个变体力。极坐标系下模型的几何方程可表示为:
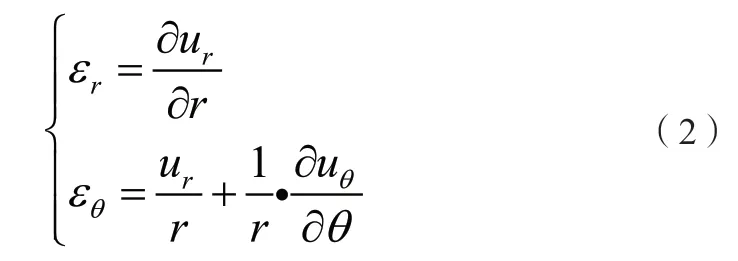
式中:ε r,εθ分别为径向、环向应变,uθ为环向位移。值得注意的是:变体力情况下,模型位移并不是轴对称的。由热弹性耦合理论导出应力分量表示应变分量的热耦合本构方程[2.3]:
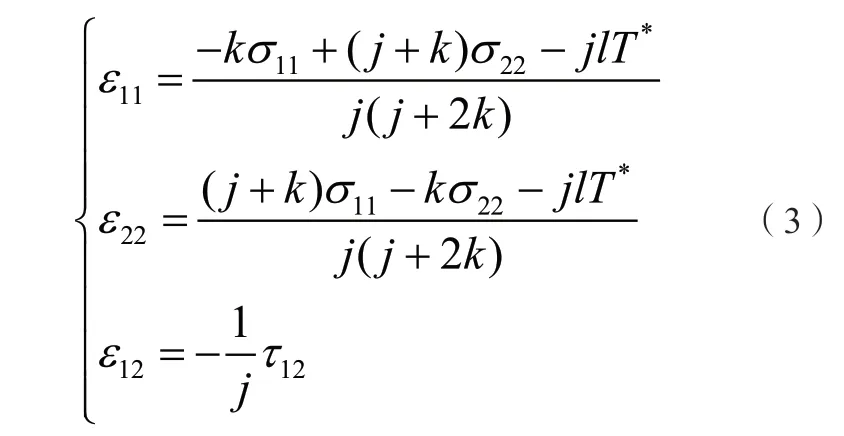
在直角坐标系中,由几何形式的相容方程及平衡微分方程推导关系,导出耦合热应力形式的相容方程:
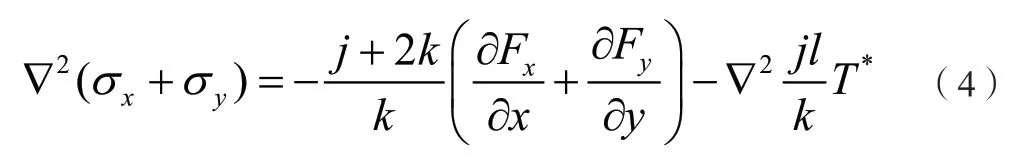
则碟片全邻域热弹性场可表示为:
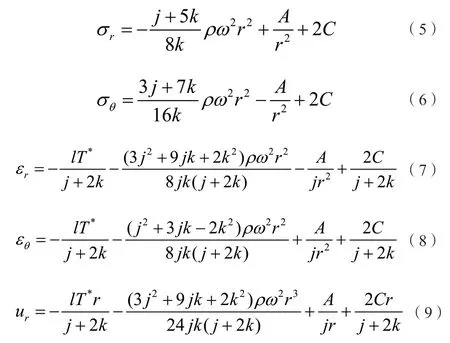
4 结果分析
研究碟片所处温度场*T、碟片转速ω及碟片板面厚度a/b对于热应力集中系数K的影响如图1 所示。
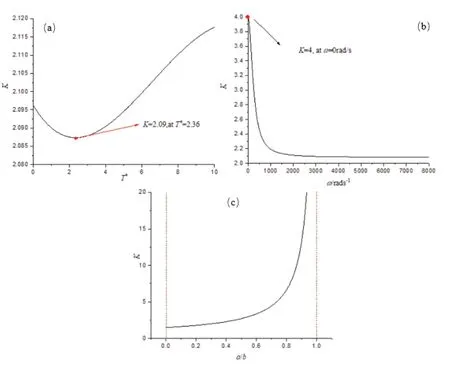
图1 模型热应力集中系数随(a)温度场 T *、(b)碟片转速ω 及(c)碟片板面厚度 a /b 变化关系
5 结语
①热弹性耦合理论导出的本构关系同样可以建立相应的相容方程,对于不同形式的温度场、体力情况可导出不同的相容方程,以均匀温度场、惯性力(变体力)为例的相容方程可进一步建立Ariy 应力函数并得到应力控制方程,相应的应力应变解析表达式明确[3]。
②薄壁旋转碟片的内径应力集中环带情况受到其温度、转速及径向厚度的影响,其中最显著的是径向厚度。
③径向厚度越薄的碟片模型内径处应力集中情况越剧烈,如内外径厚度比为0.9 的碟片应力集中系数可达13.03。以机械加工工业中的磨削砂轮为例,若想减缓砂轮内径处应力集中情况从而增加其寿命,在磨削半径即砂轮外径不变的情况下,最显著的方案为减小砂轮内径。
