提出一种新的能量动量关系式假设

陈志鹏

（泉州潜力光电科技有限公司，福建 泉州 362000）

1 摘录中国传媒大学黄志洵《波粒二象性理论的若干问题》原文

de Broglie 波的相速不是信息的速度，也不是粒子的运动速度，过去几乎无人重视de Broglie 波超光速，不认为是一个问题。但在这里我们却看到物质波与电磁波（光波）的重大区别，对后者而言在自由空间（真空）中传播的速度就是Vp=C；如果Vp>c 便称为（异常传播）需要特殊的理解和解释。故电磁波与物质波之间存在奇怪的不对等。

这是中国传媒科技大学黄志洵教授由感而发的困惑。

2 光的de Broglie 波

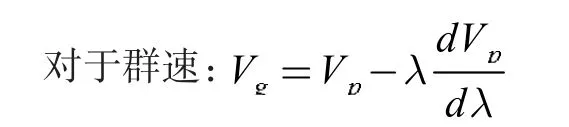
Vp为相相速，Vg为群速，λ 为波长，由非色散媒介的无色波可得dVp/λ=0，即Vg=Vp那么对于光的de Broglie 波而言，光波既要满Vg=Vp=C，同时也要满足Vp=uλ。

即光的de Broglie 波必须是一种特殊的无色群波才能满足Vg=Vp=C=uλ。

由实物粒子de Broglie 波Vp=uλ=c2/v≠（Vp=v）与光的de Broglie 波存在奇怪的不对等。

3 关于正负电子对湮灭成光子对实验

一对高能的自旋相反其它属性一致的正负电子对，在湮灭的瞬间，能产生一对光子。那么这一对光子在湮灭的瞬间是静止的，其能量表达式为为E=1/2m0c2+1/2m0c2=m0c2，那么这一对光子的动量是多少呢？用牛顿动量知道p0=0。但由于静能量m0c2不是静止的，那么上述动量表达式应该是p0=m0c2才正确，即在正负电子对湮灭的瞬间静能量等于静动量。同时对于光子的动量是mc。那么对于物质粒子如果考虑到内在能量关系式时取值应为[m0c2，mc]。

4 一种新的能量与动量关系式

为了建立新的能量与动量关系式，做如下假设：

4.1 如果de Broglie 波光是一种无色群波并满足Vg=Vp=C=uλ

4.2 那么基于光的de Broglie 波类比于物质粒子物质波的相速度与群速度也应满足波速等于波长与频率的乘积，即Vg=Vp=V=uλ 关系式。

可得：

适用范围：p=mv, 适用于理想物粒子，当不考虑粒子能量时适用。

E=PV 适用于考虑粒子内在能量时适用。

5 czp 方程Dirac 形式

对于CZP 方程Dirac 形式由：

上式可化为：E2=v4c2p2/c4+m20c4（ 设v2/c2设z）则这个方程仿照Dirac 方程先行开方形式，写出

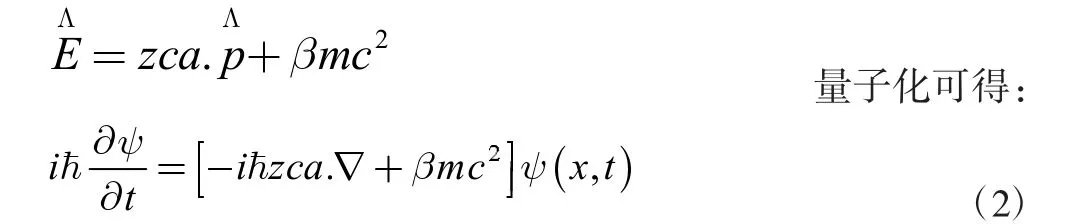
CZP 方程Dirac 形式（方程中z 为速度项可以直接做为速度修正，对于Dirac 方程的解只需做z 修正）

当实物粒子速度接近光速时，两式是趋同的。（对于大型粒子对撞机，用于测试粒子的速度都加速到非常接近光速）。且由Dirac 方程电子自旋角动量S=h∑/2π，CZP 方程Dirac 形式显然也满足。

5.1 解决μ 子实验与Dirac 计算不符

对于磁场中电子的自由运动CZP 方程Dirac 形式与电磁场耦合起来，可以写出（q=-e<0）

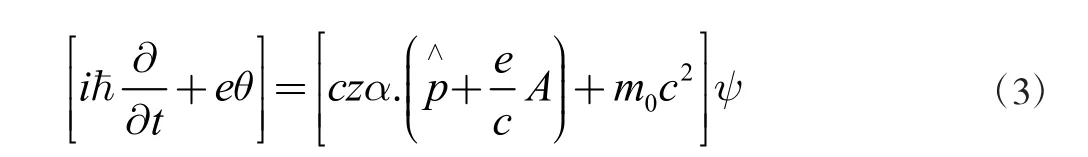
式中θ 和A 是电磁场的标势与各矢式。

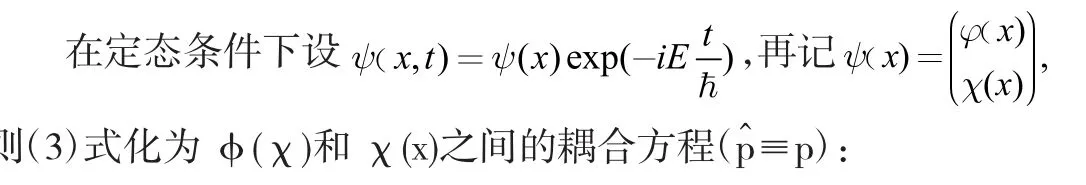
现在我们可以从（7）式看出来与Dirac 方程得到的解差了一个速度差异项。对于较轻质量的电子在费米实验室大型粒子加速器可加速到0.999999999987c 那么速度修正项Z 因子就变的不明显，只有在小数点十位以后才会表现出差异。

对于质量约为电子的207 倍的μ 子而言，在同样的加速器中μ 子却只能被加速到0.9999999974C。所以才会得到μ子的“g 因子”在实验中为2.00233184122，而根据标准方程算出的理论值却是2.00233183620。这两者之间的差异表现在Z 因子上。

μ 子g 因子由g1=gQED+gEW+gHadron

由上式Z 因子修正得到g1/g2=z (g1标准理论值，g2实验值)，即加速器中μ 子速度平方等于0.999999994985846C 那么可以计算出μ 子在加速器中速度约为0.999999997492923C。

5.2 精细结构常数

这个解值与实验一致，且不需加入人为设定的精细结构常数项。

6 关于质能动量量子方程的一维方势阱

式中A1，A2，B1，B2为特定常数。（11）式右边第一项在X→∞时X 趋近于∞。第二项B2e-qxx→∞时趋近于∞。为了保证波函数的有限性，必须在X<0，X>a 时分别取B1，B2为零，因而(12)写为：

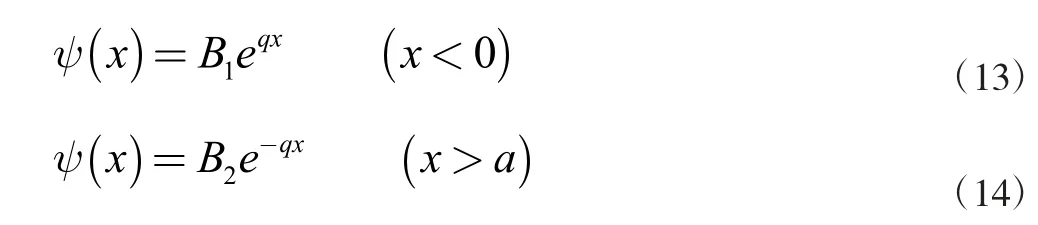
可见x<0 和x>a 的区波函数的强度也不会为零。说明，粒子的能量小于阱内外的势能差，粒子出现在阱外的概率也不为零。常数A1，A2，B1，B2可由波函数的标准条件确定。

当考虑阱深为无穷大V0→∞的简单情况时，因为V0→∞时，q→∞由（11）与（12）可知，在X<0，X>a 处ψ=0，即粒子出现的概率为零。且由于波函数在X=0，X=a 处必须连续，即ψ(0)=ψ(a)=0 代入（11）可得：A1+A2=0 与A1eika+A2e-ika=0

联立两式可得：eika-e-ika=2isinka=0

要使这个式子成立，常数K 不能取任意值，而只能取满足下式的一些不连续值：ka=±nπ n=1，2，3...

将上式代入（10）得粒子在无限深阱中粒子能量的可能取值为：

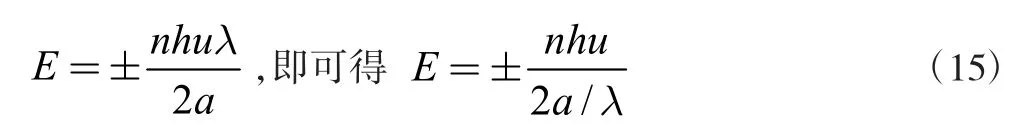
上式表明一维方势阱解有三种形态，正值，负值，或是正负值解。

7 对季灏三个实验给予解释

季灏对麻省理工学院物理系贝托齐在核科学实验室实施的用量热法验证质速关系的实验进行分析，发现贝托齐实验的理论值为0.5MeV，1.0MeV，1.5MeV，4.5MeV，15MeV 五种能量的电子。但在实验报告中仅给出1.5MeV 和4.5MeV 两种电子能量的测量值，没有给出15MeV 电子能量的测量值。季灏对此产生疑问，并对这个实验在加速器实验室中进行重新测量。加速器产生电子束流的六种标称能量和对应的狭义相对论质速关系求得的速度如表1 所示。用铅铁准直器将电子垂直射入0.1210T 的均匀磁场。按照牛顿动量代入狭义相对论的公式计算，电子的圆周运动轨道半径应当是落在10.94 厘米、16.41 厘米、24.62 厘米、32.82 厘米、43.76 厘米和54.7 厘米的六个点上。然而季灏实验却表明，所有的六种电子都落在感光胶片半径大约为18 厘米的小范围内——不同标注能量的电子的偏转半径不符合牛顿动量代入狭义相对论的预言（详见表1）。

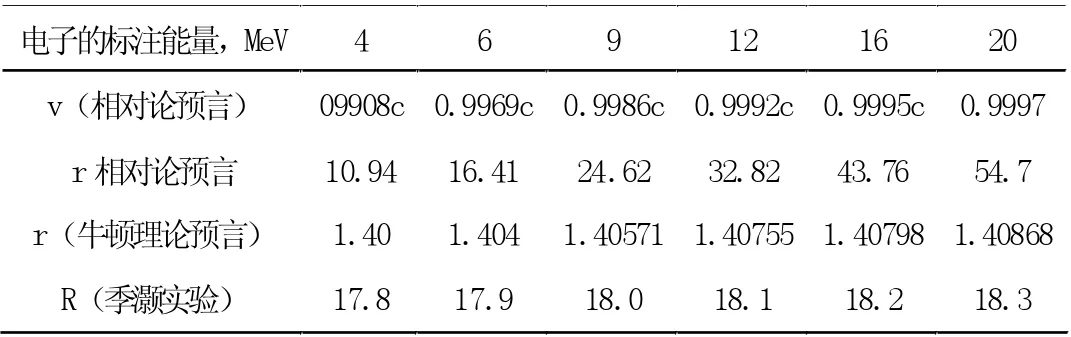
表1 季灏实验，对应的牛顿理论预言及相对论预言

采用柱坐标系，设电子在Z=0 平面运动。在均匀磁场中，令R 是粒子圆形轨道半径，P 是粒子的质能动量关系式的动量，那么代入加速器理论中常用公式并代入质能动量得到：

季灏的六种能量电子束实验表明，这六种电子都落在大约18cm 感光胶片半径上，说明具有不同能量的电子的运动轨迹几乎都落在同一个圆上。也就是说，季灏实验不符合牛顿动量代入狭义相对论理论值。如果按（16）式，则可以得到电子的圆周运动轨道半径运动约为18cm 完美的解释了季灏的实验。

8 讨论

费曼说过，这世界上没有人能真正地理解量子力学？这应是量子力学基础不牢靠造成的。随着实验的不断增加与精确测量，如缪子磁矩，质子电荷半径等与标准方程存在不可忽视的误差。这些都是很大的问题，我们有理由去讨论它们。