二叉树上非齐次分支马氏链一类强极限定理

李世林, 杨卫国, 石志岩

(江苏大学理学院，镇江 212013)

1 引言

对于树图上的每一个节点t，我们称其下一层中与它相邻的节点为节点t的子代，t为这些相邻节点的父代.本文主要考虑二叉树，记为T2，见图1，其特点在于树上的每一个节点t在下一层都有两个不同的相邻节点，即两个不同的子代，分别记为t1和t2，同时用1t表示节点t的父代.

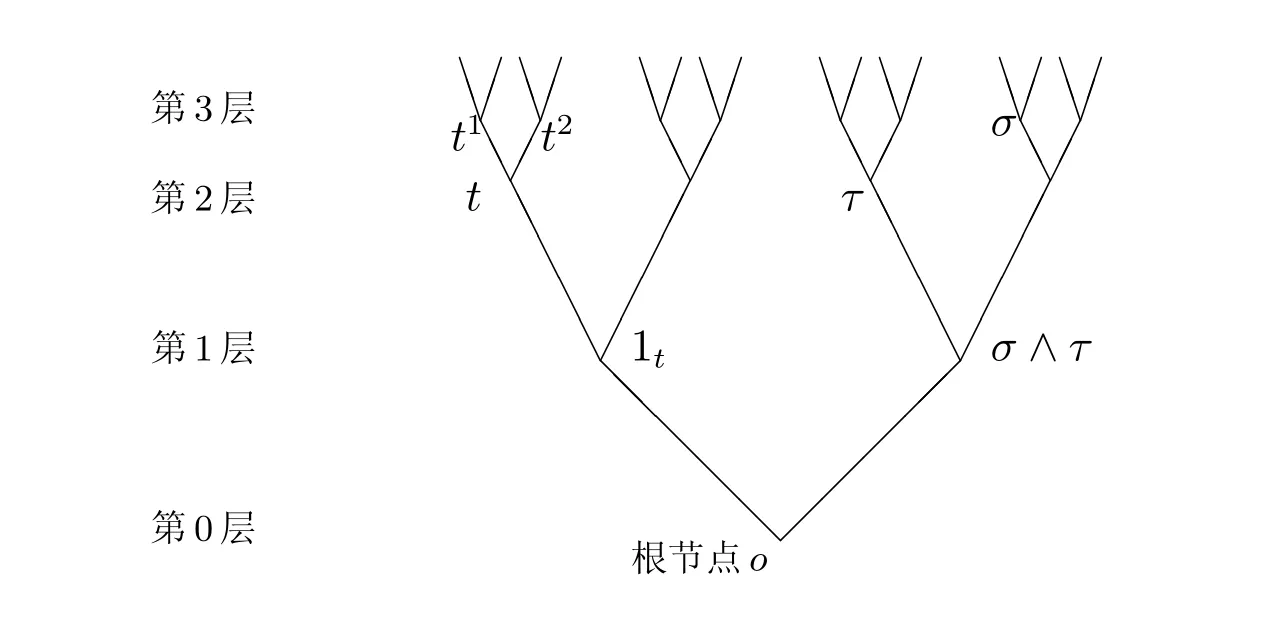
图1 二叉树T2

设(Ω,F,P)为概率空间，{Xt,t ∈T2}是定义在(Ω,F,P)上且取值于G={1,2,··· ,N}(N是正整数)的随机变量集合，设B为T2的子图，记XB={Xt,t ∈B}，xB表示XB的实现.

定义1[1]设T2为二叉树.{Xt,t ∈T2}是定义在概率空间(Ω,F,P)上在有限状态空间G={1,2,··· ,N}中取值的随机变量集合，设p={p(x),x ∈G}是G上一概率分布，P=(Pt(y1,y2|x),t ∈T2)是定义在G×G2上的一随机矩阵，满足

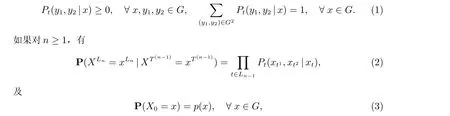
则称{Xt,t ∈T2}为具有初始分布p与随机矩阵P并在G中取值的二叉树上非齐次分支马氏链.

定义2[2]设T是局部有限的无穷树，G={1,2,··· ,N}为有限状态空间，{Xt,t ∈T}是定义在概率空间(Ω,F,P)上在G中取值的随机变量族，设

是G上一概率分布，

是定义在G2上的随机转移矩阵族.如果对于任意的顶点t，

且

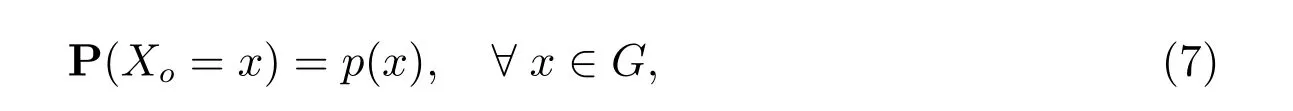
则称X={Xt,t ∈T}为具有初始分布式(4)和随机转移概率矩阵族(5)的树指标G值非齐次马氏链.

在二叉树情况下，文献[3]中指出树指标非齐次马氏链是一类特殊的非齐分支马氏链，故有如下引理.

引理1[3]设{Xt,t ∈T2}是由定义1 定义的二叉树上非齐次分支马氏链，其转移概率矩阵Pt= (Pt(y1,y2|x)), x,y1,y2∈G，如果存在转移矩阵Qt= (Qt(y|x)), x,y ∈G，使得

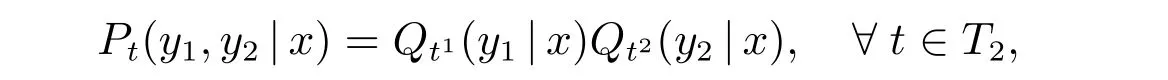
则{Xt,t ∈T2}是树指标马氏链，其转移矩阵为Qt.

近年来，树指标随机过程的极限性质被学者们广泛研究且研究成果颇丰，Benjamini和Peres[4]提出了树指标马尔科夫链的定义，并且对该模型的常返性以及射线常返性进行了研究.Dong 等[2]则考虑了在有限状态空间取值的Cayley 树指标非齐次马氏链，并给出了相应的其强大数定律及渐进均分性(AEP).Guyon[5]提出了取值于任意状态空间的二叉树上分支马氏链模型，并研究了该模型的强大数定律及中心极限定理.Dang 等[3]则在Guyon 的研究基础上建立了离散状态空间下二叉树上非齐次分支马氏链的定义，讨论了其强大数定律和熵遍历性定理，并且给出了该模型与树指标马氏链之间的等价性.随后对于有限或可列状态空间上的二叉树分支马氏链的强大数定律，Shannon-McMillan 定理以及等价性质也被广泛的讨论[1,6-8].刘文[9]率先提出了有限状态空间下非齐次马氏链随机转移概率调和平均的极限定理，石志岩和杨卫国[10]推广了上述结果，研究了一般树图上的树指标非齐次马氏链的随机转移概率调和平均的极限定理.此后，对于树上路径过程随机条件概率的调和平均，几何平均的强极限定理的研究也取得了一些成果[11,12].近期，石志岩等[13]也在马氏环境下，讨论了树指标马尔可夫链转移概率的强极限定理.本文主要考虑在有限状态空间G上取值的二叉树上非齐次分支马氏链的一类强极限定理，首先我们给出了二叉树上非齐次分支马氏链的强极限定理，进而利用该极限定理研究了其随机转移概率调和平均的强极限定理，最后借助于文献[3]中给出的二叉树上树指标非齐次马氏链与非齐次分支马氏链的等价性质，指出了树指标马氏链调和平均的强极限定理可作为本文所得结果的一个推论.

2 主要结果

引理2[3]设T2为二叉树，{Xt,t ∈T2}是如定义1 所定义的在有限状态空间G上取值的二叉树上非齐次分支马氏链，gt(x,y1,y2)是定义在G3上的函数族.设L0={o}, Fn=σ(XT(n))，则其中λ为实数，则{tn(λ,ω),Fn,n ≥1}为非负鞅.

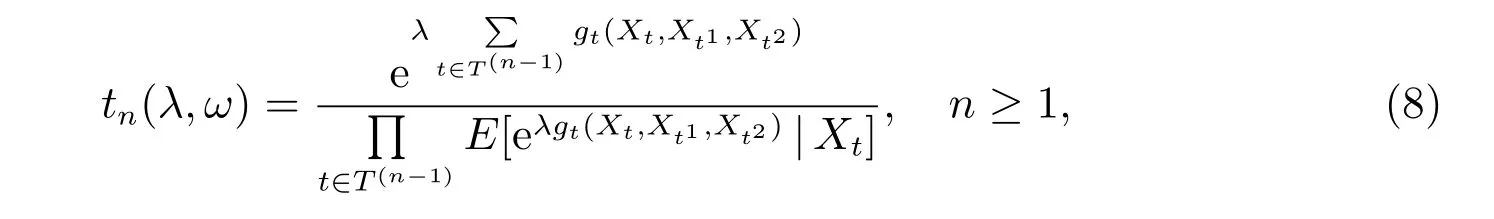
定理1 设T2, {Xt,t ∈T}, gt(x,y1,y2)如引理1 所定义，{an,n ≥1}为非负随机变量序列，设α ＞0，则

当|λ|＜α，利用不等式

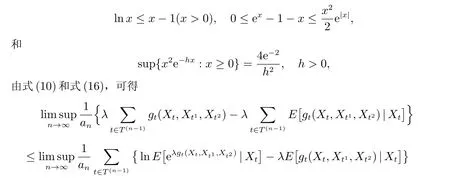
当0＜λ ＜α时，式(17)两侧同除λ，注意到式(11)和式(12)，有

于是由式(19)和式(20)，可知式(13)成立.

注1 文献[3]中研究了与之相似的二叉树上非齐次分支马氏链的强极限定理，其使用的条件为

本文则在新的条件下研究了该强极限定理，所得结果更易于推出二叉树上非齐次分支马氏链随机转移概率调和平均的极限定理及树指标非齐次马氏链随机转移概率调和平均的极限定理.

推论1 设T2是二叉树，X={Xt,t ∈T2}, {gt(x,y1,y2),t ∈T2}, Hn(ω)与Gn(ω)如定理1 中所定义.如果存在α ＞0，使得对任意的ω ∈Ω，有

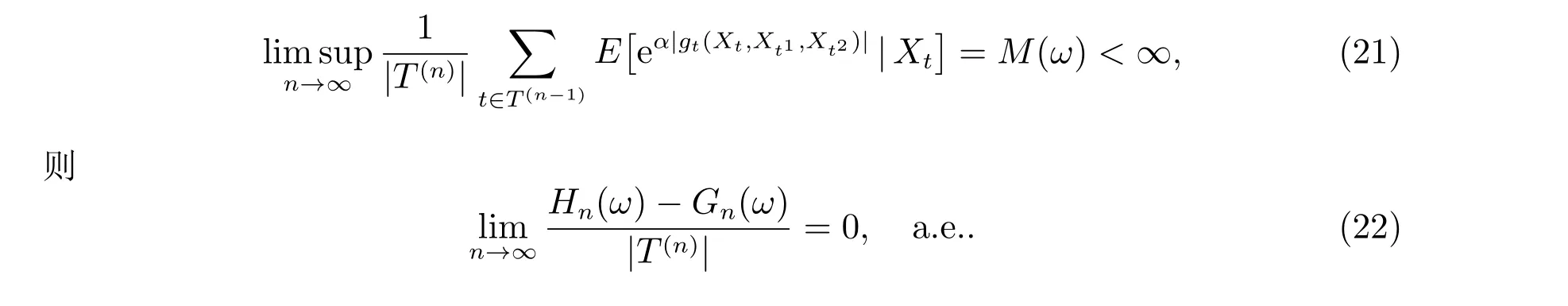
证明 令an=|T(n)|，由式(21)可知D(α)=Ω，故由定理1 可得本推论成立.

接下来，利用推论1 可以得到二叉树上非齐次分支马氏链转移概率调和平均的强极限定理.

定理2 设{Xt,t ∈T2}是如上定义的二叉树上非齐次分支马氏链，其初始分布和转移概率族分别为故由式(31)，可得推论2 成立.

下面说明由推论2 可以推出文献[10]中树指标非齐次马氏链转移概率矩阵的极限定理.

推论2[10]设T2是二叉树，{Xt,t ∈T2}是由定义2 定义的树指标非齐次马氏链，其初始分布和转移概率族分别为