微流程模型的效率改进*

施正香 ，罗文杰 ，孙建东 ，周 洋 ，杨俊刚

(1.云南电网有限责任公司 迪庆供电局，云南 迪庆 674400；2.西南林业大学 大数据与智能工程学院，云南 昆明 650224；3.云南云电同方科技有限公司，云南 昆明 650217)

0 引言

业务流程管理是组织用来构建和更新信息系统的主要技术之一[1]。其关键思想是业务流程用业务流程模型来建模，而信息系统的开发通过流程模型来驱动[2]。从控制流视角，业务流程模型描述了为完成某些业务目标应该执行哪些任务以及它们的执行顺序；从数据视角，业务流程模型描述了应该处理的数据；从资源视角，业务流程模型描述了谁应该负责什么任务。

为了快速响应客户需求，应该持续演化信息系统。为了支持更好地持续演化，业务流程管理要求业务流程微化[3]。相比传统的业务流程，微流程为特定条件下不可再分解的业务流程。当微流程模型被建模后，一个关键问题是能否改进该模型的效率[4]。例如，原本可并发执行的两个任务在微流程模型中被建模为顺序执行。因此，该流程模型的执行效率是低效的。

改进微流程模型是指在不改变外部行为的情况下修改流程模型内部结构的过程[5-6]。现有研究工作主要关注改进业务流程模型的可理解性、可维护性。在改进业务流程模型的可理解性方面，文献[7]提出了一种对业务流程模型的活动进行自动标注的方法；文献[8]提出使用动词-宾语的样式对业务流程模型的活动进行标注，从而提高了业务流程模型的可理解性；文献[9]提出了一种活动标签的样式转换方法，用于将名词样式转换为动词-宾语的样式；文献[10]提出了一种活动标签样式的分类方法，用于将样式分为名词样式和动词-宾语的样式；文献[11]提出了一种方法，用于将活动标签样式进一步细分。在提高业务流程模型的可维护性方面，文献[12]提出了一种用于提高流程模型库中流程模型可维护性的方法；文献[13]提出了一种识别低维护性模型的方法；文献[14]提出了11 个业务流程模型的重构操作，用于提高模型的可维护性。与上述工作相比，本文工作的最大不同在于重点关注改进微流程模型的效率。

具体而言，本文提出了一种改进微流程模型效率的方法，主要贡献如下：(1)根据微流程模型的结构，提出了提取任务关系的算法；(2)从数据视角，提出了分析任务间数据依赖关系的算法。

1 微流程的建模

以Petri 网为形式化基础[15]，本文采用文献[2]提出的带数据的工作流网(WorkFlow net with Data，DWF-net)对微流程进行建模。

定义1(工作流网)[16]工作流网是一个6 元组WF-net=(P，T；F，M，i，o)，其中：

(1)P∪T≠Ø∧P∩T=Ø，P 为库所集，T 为任务集；

(2)F⊆(P×T)∪(T×P)是流关系；

(3)映射M：P→(0，1，…)表示工作流网的标识；

(4)i∈P 表示输入库所；

(5)o∈P 表示输出库所；

(6)每一个节点x⊆P∪T 都位于从i 到o 的一条路径上。

定义2(微流程)微流程是一个9 元组MP=(P，T；F，D，I，O，M，i，o)，其中：

(1)WF-net=(P，T；F，M，i，o)为工作流网；

(2)D 为WF-net 操作的数据集；

(3)I：D→2T输入函数，描述任务的输入数据；

(4)O：D→2T输出函数，描述任务的输出数据。

在微流程的图形化表示中，本文用圆圈表示库所，用方框表示任务，用有向线段表示流关系。

以文献[4]中的在线购物为例，图1 使用定义了微流程模型。首先，麦基通过互联网在线订购商品(任务A)，任务A 的输出是商店地址(变量m)和买家的地址(变量n)。其次，买家可以选择自取或邮寄来提取货物。如果买家选择自取方式(任务B)，他根据商店地址(变量m)到商店提货(变量o)。在收到货物(任务C)后，买家将收到卖家的收据(变量q)。另一种情况，如果卖家选择邮寄方式，卖家需要准备货物(任务D)，并确保货物将邮寄到正确的买家地址(变量n)。为此，卖家将联系快递员(任务E)，货物将被包装上买家地址(变量n)，同时生成跟踪号(变量p)。快递员交付(任务F)包裹给买家(变量o 和变量p)，买家接收货物和收据(变量q)。在货物和收据(变量q)检查无误后，买方确认接收货物(任务G)，交易成功结束。

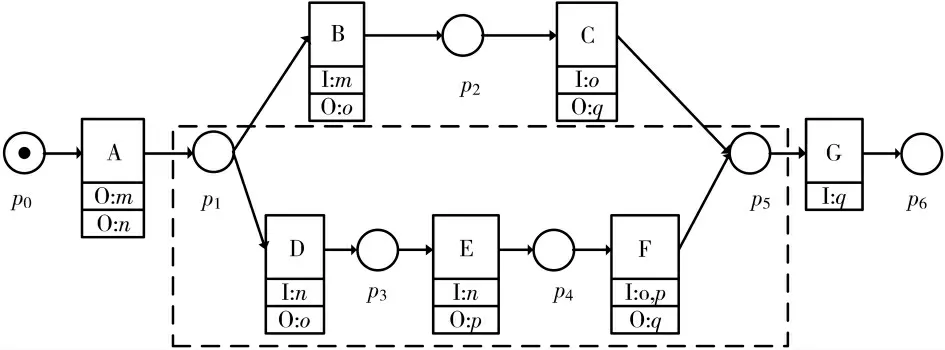
图1 在线购物微流程

对于图1 所示的线购物微流程模型，从控制流视角，任务D 和任务E 是串行执行的。但是，从数据视角，由于任务D 和E 没有任何数据依赖，故而，它们可以并行执行。

针对上述分析，从提高模型执行效率的角度，本文对图1 所示流程模型进行改进，使得模型中没有数据依赖的任务都并行执行。

定义3(任务发生规则)微流程9 元组MP=(P，T；F，D，I，O，M，i，o)，并具有下述的任务发生规则：

(1)对于任务t∈T，如果∀p∈*t：M(p)≥1，则说明任务t 在标识M 有发生权，记为M[t＞；

(2)若M[t＞，则表示在标识M 下，任务t 可以发生，发生后得到一个新标识M′，记为M′[t＞M，∀p∈P，满足：

①若p∈*t-t*，则M′(p)=M(p)-1；

②若p∈t*-*t，则M′(p)=M(p)+1；

③其他，则M′(p)=M(p)。

(3)通常用M0表示初始标识；

(4)一个任务发生序列σ=t0，t1，…，tn-1使从初始标识M0到达标识Mn，可标记为M0→σMn。

2 效率改进的流程

图2 直观描述了本文所提改进流程的步骤，具体包含4 个步骤：提取任务关系、分析数据关系、更新任务关系、重构模型。

图2 效率改进的流程图

2.1 提取任务关系

根据微流程模型的结构，算法1 描述了如何提取任务关系。由文献[2]、[4]、[5]可知，流程模型中任务关系可细分为3 种关系：顺序(→)、选择(#)和并行(||)。

算法1：提取任务关系算法

输入：MP=(P，T；F，D，I，O，M，i，o)是一个微流程模型

输出：关系矩阵RM

(1)for p∈P do

(2) for t1∈*p do

(3) for t2∈p* do

(4) 在RM 中设置t1→t2

(5)for t1∈T do

(6) for t2∈T do

(7) if t3∈T 是t1和t2的最近汇聚节点∧t1≠t3∧t2≠t3then

(8) 在RM 中设置t1# t2

(9)for t1∈T do

(10)for t2∈T do

(11) if t1和t2不是→∧t1和t2不是# then

(12) 在RM 中设置t1||t2

需要说明的是，算法1 中的*p 和p* 分别表示库所的前集和后集，具体定义为：对于任一节点x∈X=P∪T，*x={y∈X|(y，x)∈F}，x*={y∈X|(x，y)∈F}。

令m 和n 分别表示微流程模型中库所和任务的个数，则算法1 的最坏时间复杂度为：O(m3)。

2.2 分析数据关系

分析数据关系是指检测两个任务间是否存在数据依赖关系。由文献[4]、[5]可知，数据依赖关系可细分为3 种关系：直接数据依赖(δd)、间接数据依赖(δa)和输出数据依赖(δo)。

根据任务的输入和输出，算法2 描述了如何分析数据依赖。

算法2：分析数据依赖算法

输入：MP=(P，T；F，D，I，O，M，i，o)是一个微流程模型

输出：数据关系矩阵DM

(1)for t1∈T do

(2) for t2∈T do

(3) if O(t1)∩I(t2)≠Ø then

(4) 在DM 中设置t1δdt2

(5)for t1∈T do

(6) for t2∈T do

(7) if O(t2)∩I(t1)≠Ø then

(8) 在DM 中设置t1δat2

(9)for t1∈T do

(10)for t2∈T do

(11) if O(t1)∩O(t2)≠Ø then

(12) 在DM 中设置t1δot2

令n 表示微流程中任务的个数，则算法2 的最坏时间复杂度为：O(n2)。

2.3 更新任务关系

基于关系矩阵RM 和数据关系矩阵DM，算法3 描述了如何更新任务关系。其核心思想是如果两个任务是顺序关系，但没有任何数据依赖关系，则该顺序关系可以更新为并行关系，以改进流程模型的效率。

算法3：更新任务关系算法

输入：MP=(P，T；F，D，I，O，M，i，o)是一个 微流程 模型，关系矩阵RM 和数据关系矩阵DM

输出：更新后的关系矩阵RM

(1)for t1∈T do

(2) for t2∈T do

(3) if RM 中t1→t2∧DM中t1与t2没有任何数据依赖关系then

(4) 在RM 中设置t1||t2

令n 表示微流程中任务的个数，则算法3 的最坏时间复杂度为：O(n2)。

2.4 重构模型

针对算法3 输出的更新后的关系矩阵RM，算法4借鉴α 算法[17]的思想，描述了如何重构流程模型。其核心思想是如果任务间具有顺序关系，则构建库所，使得任务通过库所相连。

算法4：重构模型算法

输入：关系矩阵RM

输出：WF-net=(P，T；F，M，i，o)

(1)for t1∈T do

(2) for t2∈T do

(3) if RM 中t1→t2then

(4) P=P∪{p12}

(5) F=F∪{(t1，p12)}∪{(p12，t2)}

(6)for t1∈T do

(7) if *t1==Ø then

(8) P=P∪{i}

(9) F=F∪{(i，t1)}

(10)if t1*==Ø then

(11) P=P∪{o}

(12) F=F∪{(t1，o)}

令n 表示微流程中任务的个数，则算法4 的最坏时间复杂度为：O(n2)。

3 实验

3.1 工具

本文采用开源工具PIPE(Platform Independent Petri net Editor)对微流程进行建模。PIPE[18]是一个开源的Petri 网建模和分析工具，被学术界广泛使用。

图1 所示在线购物微流程在PIPE 工具的建模实现如图3 所示。图4 描述了改进后的在线购物微流程在PIPE 工具中的建模实现。

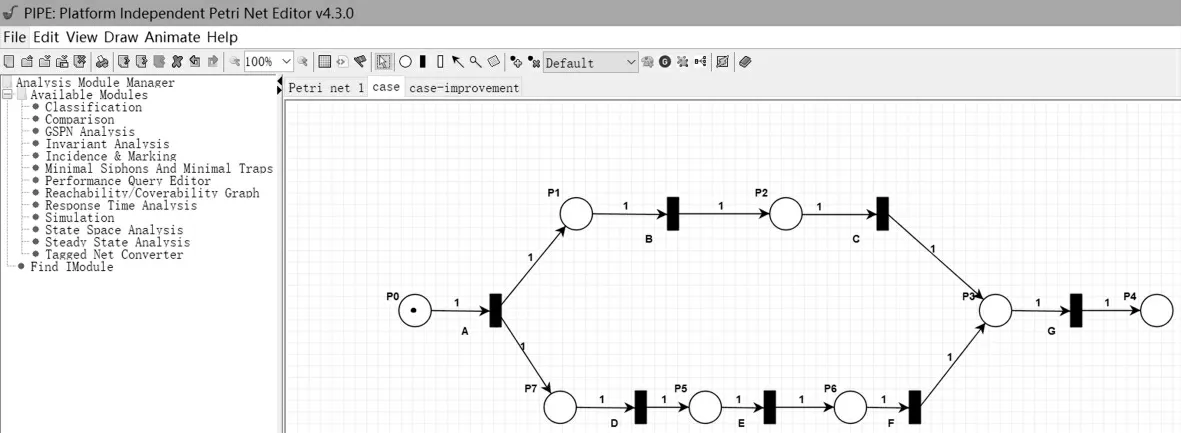
图3 在线购物微流程的建模实现截图

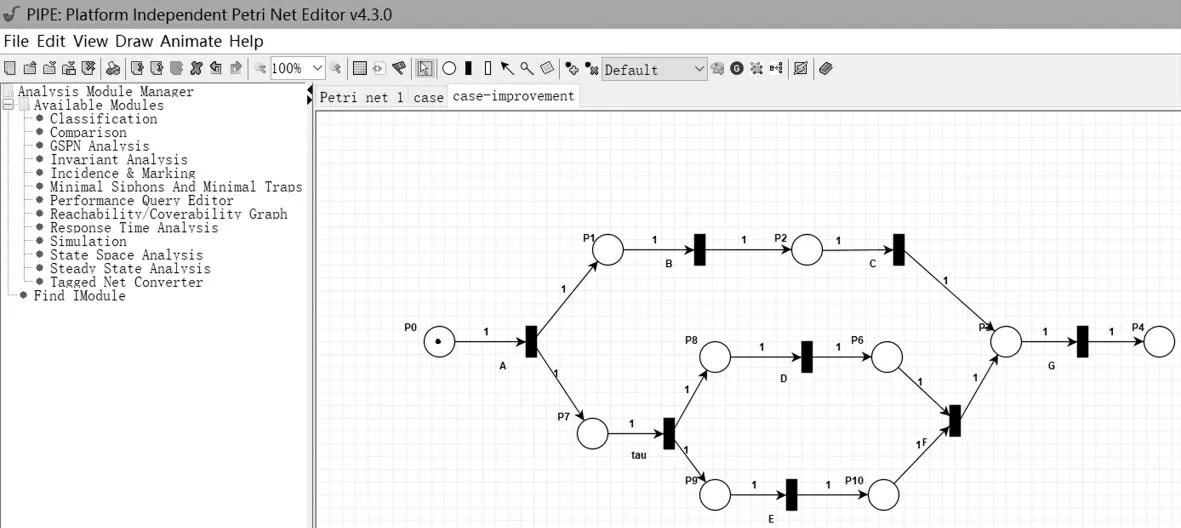
图4 改进后在线购物流程建模实现截图

3.2 实验结果

本文的实验数据集来源于BPM AI 过程模型库。BPM AI 中有学术界和工业界创建的大量真实流程模型，共计400 多个。表1 给出了部分实验结果。

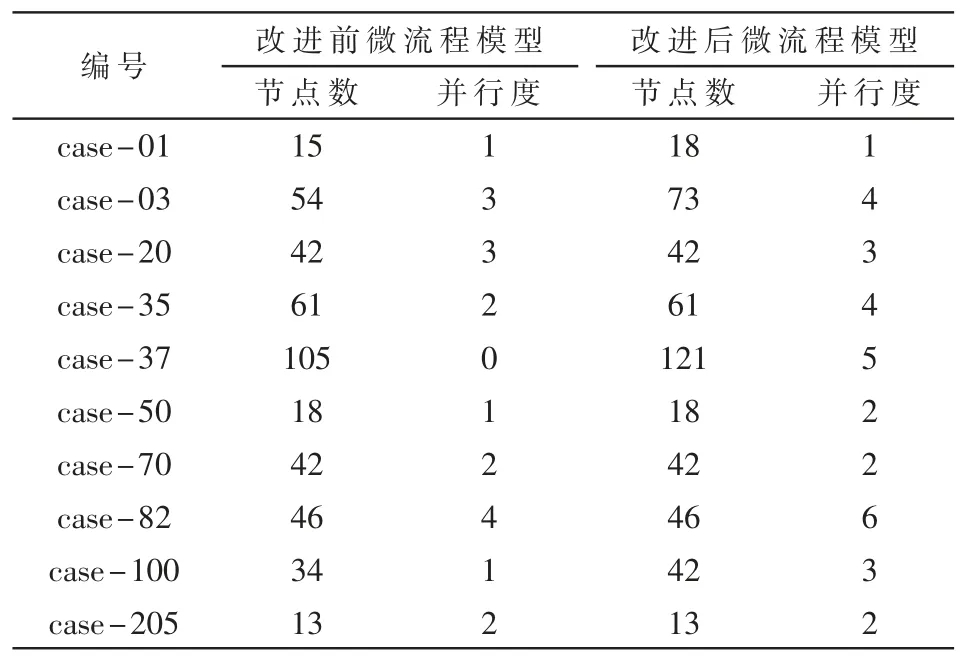
表1 部分实验结果

为了度量微流程模型的并行度，本文基于文献[2]中的任务出度，提出了并行度CD：

其中，dout(t)表示任务t 的出度。

表1 第1 列为编号，第2 列为改进前微流程模型的节点数和并行度，第3 列为改进后微流程模型的节点数和并行度。

从表1 可知：(1)案例case-20 和case-70 改进前后并行度不变，说明这两个流程模型中有顺序关系的任务也有数据依赖关系；(2)案例case-01、case-03、case-37和case-100 改进前后并行度和节点数均增大，说明在提高这些流程模型并行度的同时，也增加了节点数；(3)案例case-35、case-70、case-82 和case-205 改进前后并行度增大，说明在提高这些流程模型并行度的同时，这些流程模型中存在有顺序关系的任务没有数据依赖关系。

4 结论

为提高微流程模型的质量，本文使用带数据的工作流网，提出了一种改进微流程模型效率的方法。该方法通过提取任务关系、分析数据依赖、更新任务关系和重构模型4 个步骤，将流程模型中无数据依赖关系的任务间的顺序关系更新为并发关系，以提高模型的效率。实验结果表明了该方法的有效性。