基于Stacking 模型融合的串联故障电弧检测

王 毅 ，陈 进 ，李松浓 ，陈 涛 ，戴莲丹 ，宣 姝

(1.重庆邮电大学 通信与信息工程学院，重庆 400065；2.国网重庆市电力公司电力科学研究院，重庆 400014；3.国网重庆市电力公司营销服务中心，重庆 400023)

0 引言

电弧是一种由于绝缘介质被电压击穿而导致的持续放电现象，通常伴随着电极部分挥发[1-2]。在生活中由于输电线长时间带载、过载产生热量或者由于外力导致的绝缘层老化、破损，会产生电弧现象[3-4]。这类电弧是人们不希望产生的，称为故障电弧[5-6]。

近年来，相关学者从不同角度对故障电弧的检测进行了广泛研究，文献[7]通过快速傅里叶变换(FFT)得到电流的幅度谱，再对其进行稀疏表示来进行故障检测，在对稀疏表示的Lp 范数进行调整时，发现对不同的数据采用不同的范数可以提高分类的准确性。文献[8]分别分析了小波熵算法、基于支持向量机(SVM)和逻辑回归的分类模型，综合以上算法可知相对于简单方法，该组合算法具有更好的检测功能。文献[9]集中讨论了电弧电流中的40～100 kHz 的高频谐波部分，通过FFT 和阈值设置，可以有效识别故障电弧。文献[10]提取电流中的9 个时频域特征，再使用主成分分析将9 个特征在维度上缩减为3 个参数，最后使用SVM 建立了负荷识别和串联电弧检测的综合模型。

上述故障识别均从故障的高频分量入手，通常需要高采样频率和高计算量。本文通过实验采集大量电流，各种信息混合情况下传统机器学习算法表现不佳，本文提出一种Stacking 模型融合的时域故障电弧检测方法，经验证该算法的识别率能达到98%以上。

1 信号采集与分析

1.1 电流信息采集平台

本文根据GBT 31143-2014《电弧故障保护电器的一般要求》选用故障电弧发生器，根据各公开文献对家用电器的大致分类选用多个典型负载采集电流信息，实验采集原理如图1 所示。

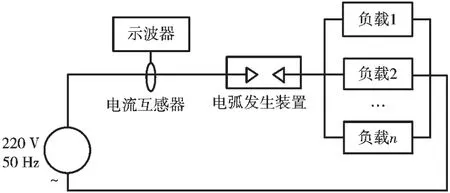
图1 电流信息采集系统

本文使用白炽灯、电风扇、电烙铁、调光灯、LED 灯和笔记本作为典型负载进行测量，使用电流互感器和picoscope高性能示波器作为电流采集工具，采样频率为10 kHz。在采集故障电流时，根据GB14.287.4-2014《电器火灾监控系统第4 部分：故障电弧探测器》规定电弧持续时间不超过0.42 ms 或者不超过额定电流值5%的微小电弧不作为电弧统计。

如图1 所示，采集正常电流时不接入故障电弧发生器，利用示波器与电流互感器相连测量电流；采集故障电流时串联接入故障电弧发生器，实验开始前旋转故障电弧发生器移动电极的螺杆使紫铜锥棒与固定电极石墨圆棒接触，此时电路闭合，实验开始后缓缓旋转螺杆将移动电极拉开使故障电弧发生器内产生连续电弧，保存此段电流作为故障电流。使用上述方法采集6 种不同类型用电器单独和混合电流波形。

采集不同类型用电器混合工作状态下的正常和故障电流，用电器功率信息如表1 所示，采集样本信息如表2 所示。

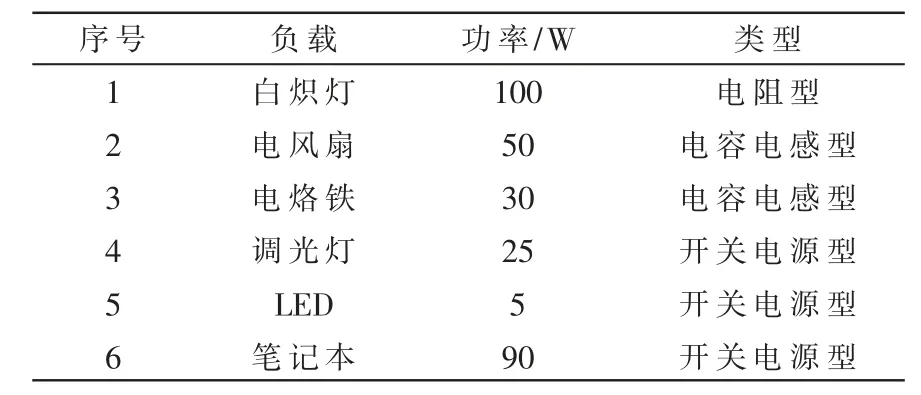
表1 典型负载

选取表1 中所示的负载作为典型负载进行测量。采集的电流信息包括各种电器单独工作以及不同类型用电器同时工作时正常和故障电流信息。采集电器和采集到的电流样本情况如表2 所示。

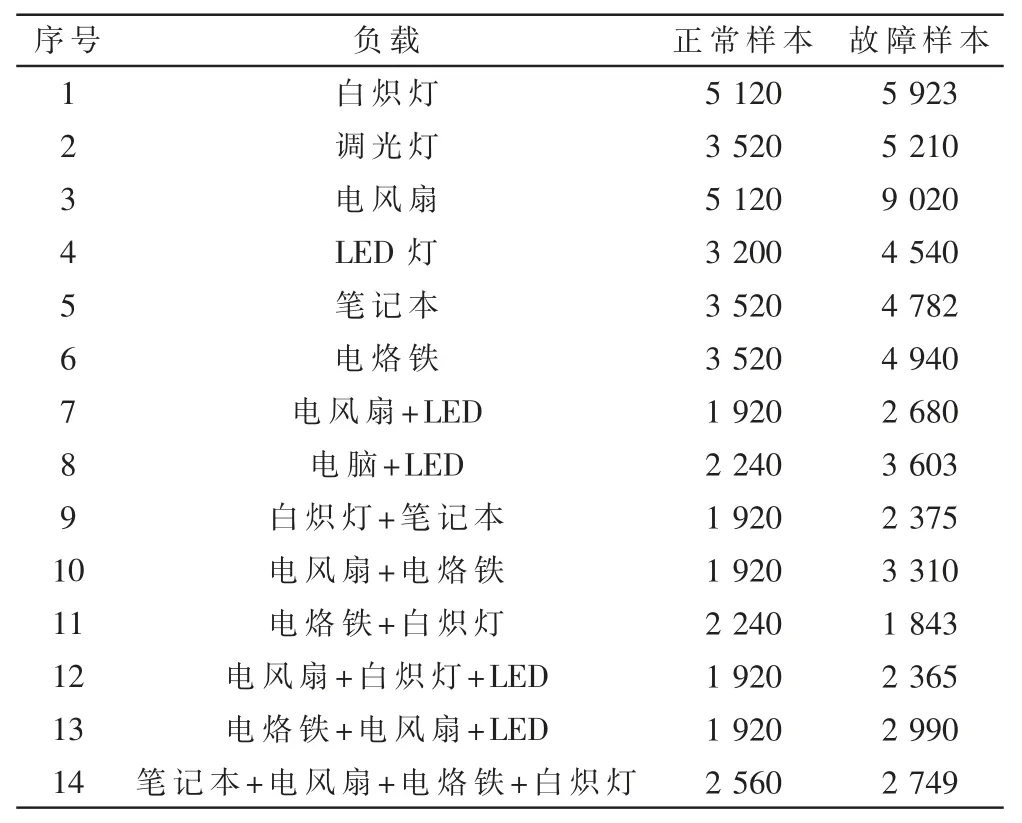
表2 电流信息采集情况

1.2 典型负载电流信息分析

本文主要针对低压交流故障电弧进行检测，此类故障电弧的一般特性为：故障电弧信号中含有高频噪声；电弧电流上升速度快于非电弧电流；电弧电流存在“平肩部”[2]。分别取白炽灯、笔记本正常和故障电流的5 个周期进行归一化后绘制图2 所示电流波形。

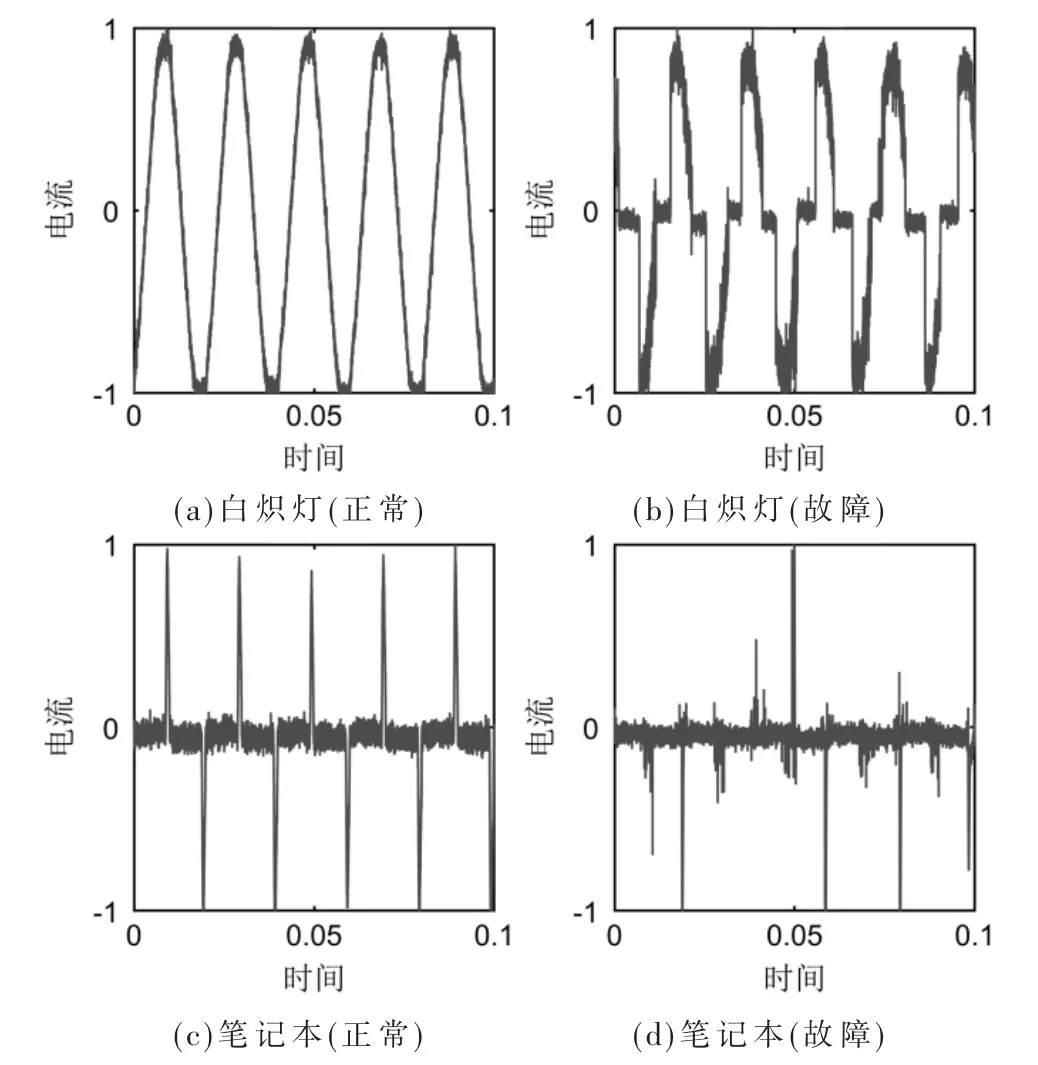
图2 白炽灯和笔记本正常和电弧状态电流波形

2 机器学习算法

2.1 机器学习

机器学习是一门多领域交叉学科，涉及概率论、统计学等多门学科[11]。机器学习算法可分为三大类：监督学习、无监督学习和半监督学习。本文主要使用监督学习算法进行故障电弧检测，将所有正常电流的类标签设为1，故障电流数据类标签设为2。

提取时域电流数据的平均值、中位数、方差以及极差进行故障识别。表3 为求解上述特征的表达式。其中，N 表示一个电流周期内的采样电流个数；xi表示当前电流周期内的第i 个电流样本。

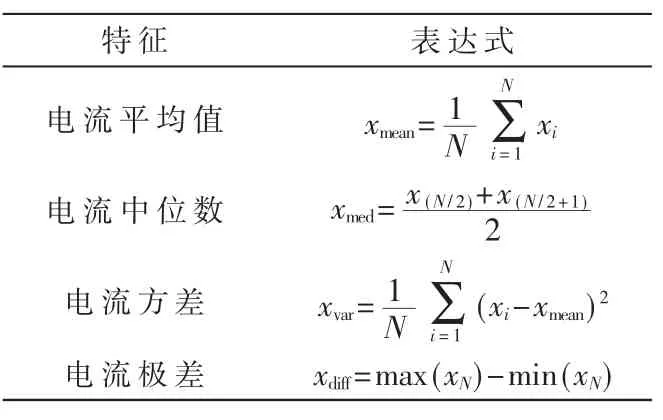
表3 时域特征表达式

本文选取决策树进行故障识别，决策树是一种树形结构[12]，由节点和有向边组成。节点有两种类型：非叶子节点和叶子节点。非叶子节点表示一个特征或属性,叶子节点表示一个类。决策树结构如图3 所示。

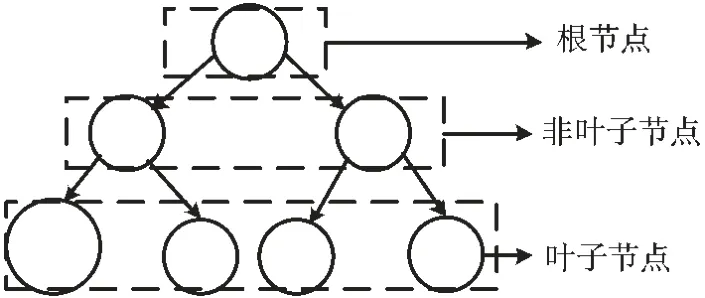
图3 决策树结构

决策树的学习本质上是从训练集中归纳出一组分类规则，得到与数据集矛盾较小的树形结构。决策树学习的损失函数通常是正则化的极大似然函数，通常采用启发式方法，近似求解这一最优化问题。

2.2 决策树参数选择

本文使用网格搜索法对决策树的最大深度进行寻优。网格搜索法首先为想要调参的参数设定一组候选值，然后穷举参数的组合，再根据设定的评分机制找到最好的设置。本文设定决策树的最大深度从1 到20 依次递增，取表2 中14 种用电器的正常和故障电流信息各1 500 组组成样本集，将样本集按照5 份切分进行交叉验证，将5 次测试集准确率的平均值作为评分标准，找到评分最高的组对应的最大深度作为最优值进行决策树建模。过程如图4 所示。

图4 为具有交叉验证的网格搜索法。上述方法在Python3.8 环境下仿真可得仿真结果，如图5 所示。

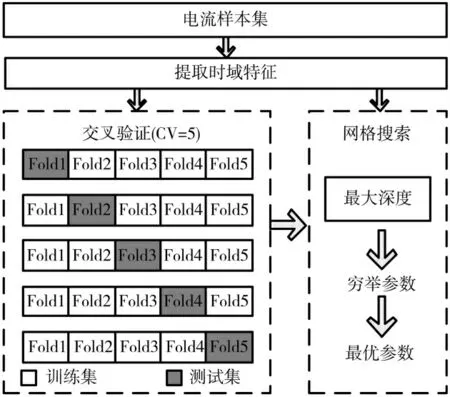
图4 具有交叉验证的网格搜索法

由图5 可得出决策的最大深度最优值为14，最优识别率为94.11%。现考虑使用集成机器学习的方法对改模型进行改进，提高故障识别率。

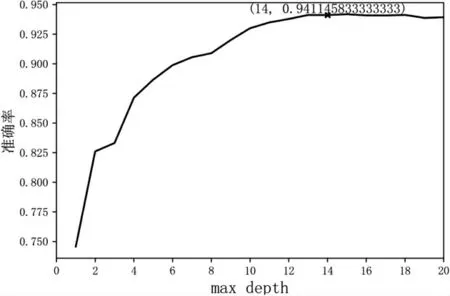
图5 决策树参数寻优

3 集成学习及Stacking 模型融合算法

3.1 Bagging 及Boosting 集成机器学习框架

集成学习将训练集数据输入若干弱学习器，通过一定的结合策略，最终可以得到一个强学习器[13-14]。

集成方法可分为两类：第一类是串行集成方法，其中参与训练的弱学习器按照顺序生成(Boosting 框架)。序列方法的原理是利用弱学习器之间的依赖关系，通过对之前训练中错误标记的样本赋值较高的权重，可以提高整体的预测效果。另一类是并行集成方法，其中参与训练的弱学习器并行生成(Bagging 框架)。并行方法的原理是利用弱学习器之间的独立性，通过平均可以显著降低错误。

本文选择基于bagging 框架的随机森林和极限树以及基于boosting 框架的Adaboost 和XGboost 算法对决策树进行优化。

随机森林和Adaboost 选择14 作为每棵树的最大深度。其基学习器个数使用参数寻优的方法，以算法耗费的时间和准确率为评分机制，找到最佳参数。集成算法准确率如图6 所示。

图6 中随着树数量的增加，算法准确率也有所增加，其中Adaboost 在树数量增加64 后，准确率基本不上升但耗费时间会增多，故对于Adaboost 来说，选择64 棵树作为基学习器是合适的；随机森林在100 棵树的条件下准确率较高，同时耗费的时间不多，故选择100 棵树作为随机森林的基学习器。

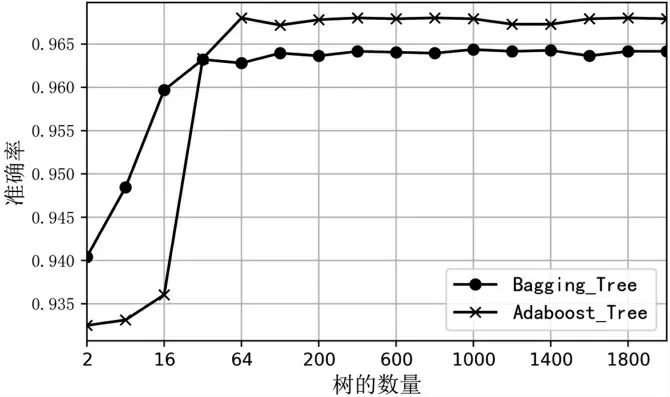
图6 集成算法准确率

对于极限树和XGboost 算法的最大深度和树的数量，首先在1～1 000 以内按200 划分为5 份，在每份中分别按10 划分寻找最优值。对于极限树和XGboost，表4 和表5 分别表示网格搜索得到的最优值。

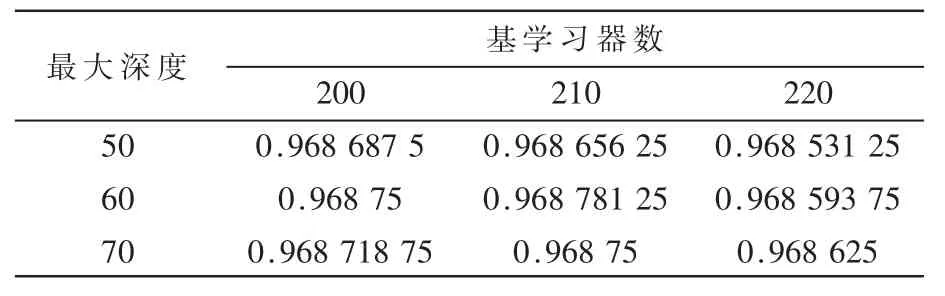
表4 极限树参数寻优

表5 XGBoost 参数寻优

极限树最大深度从10 至100 按间隔10 递增，基学习器个数从100 至300 按10 递增。表4 列出了最大深度50 至60、基学习器200 至220 的准确率，从表中可看出最大深度为60、基学习器210 时准确率最高，故后续仿真中极限树的参数均以上述数值为准。

XGboost 最大深度从8 至10 间隔2 递增，基学习器个数从10 至200 间隔10 递增。表5 列出了最大深度8至12、基学习器个数110 至130 对应的准确率，可得最大深度为10，基学习器120 个时准确率最高。

3.2 Stacking 模型融合

将个体学习器结合在一起时使用的方法叫作结合策略。有一种结合策略是使用另外一个机器学习算法来将个体机器学习器的结果结合在一起，这个策略就是Stacking[15]。

本文区别于常用的将机器学习算法作为基学习器的方法，将经过参数寻优的集成机器学习模型作为基学习器进行Stacking 模型融合。在Stacking 方法中次级学习器一般使用线性算法，本文使用逻辑回归算法作为次级学习器。

图7～图10 分别表示在不同训练集下提升树、随机森林、极限树、XGBoost 以及Stacking 集成算法的准确率、精确率、召回率以及F1 指标。其中，Stacking 使用前4 种集成机器学习算法作为初级学习器。

准确率是分类正确的样本个数占总样本个数的比例，是分类问题中最简单最常用的评价指标。如图7 所示，本仿真中4 种算法的准确率随着样本数量的增大而有所增加，但其识别率基本处于95%以上，在样本集大的情况下，准确率能达到97%以上，相较于非集成算法决策树而言，准确率有所提升。且Stacking 模型融合算法准确率在集成学习的基础上又有所提升，在样本量较大的情况下，准确率能达到98%-99%。

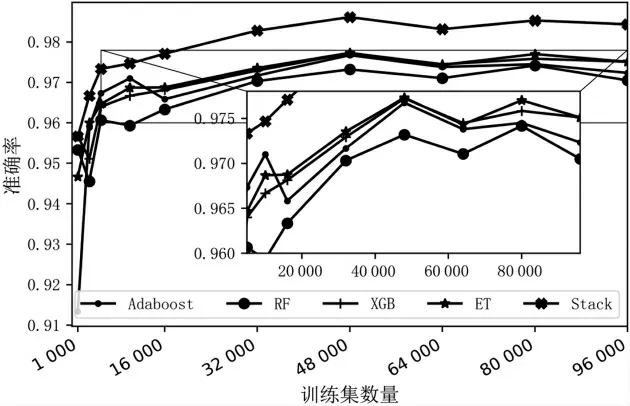
图7 算法准确率

在本文仿真中，正常电流特征被标记为正例，故障电流特征被标记为反例。精确率指模型预测为正的样本中实际也为正的样本占被预测为正的样本的比例，体现了模型对负样本的区分能力，精确度越高，模型对负样本的区分能力越强。本文提出的故障电弧检测算法主要需要检测出电流中的负样本。如图8 所示，Stacking 集成算法精确度不论在大样本还是小样本情况下都明显高于其他算法。

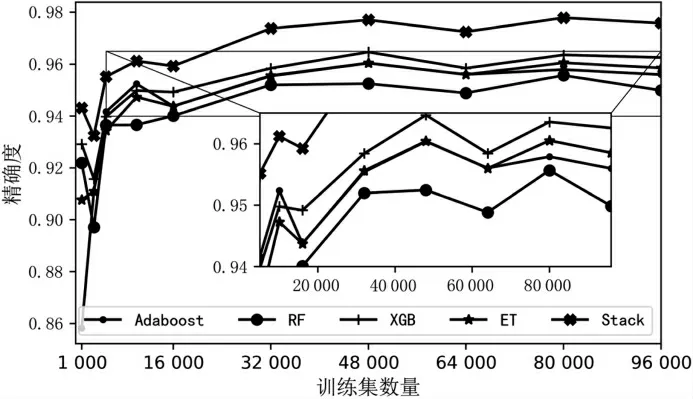
图8 算法精确率

召回率指实际为正的样本中被预测为正的样本所占实际为正的样本的比例，体现模型对负样本的识别能力，召回率越高，模型对正样本的识别能力越强。对于本文，召回率可以认为是正常样本被错判为故障样本的比例，召回率越高，其误判的可能性越低。如图9 所示，在样本量较大的情况下Stacking 算法在召回率上也有很好的表现。就此指标来说，Stacking 算法在误报率上也有很好的性能。

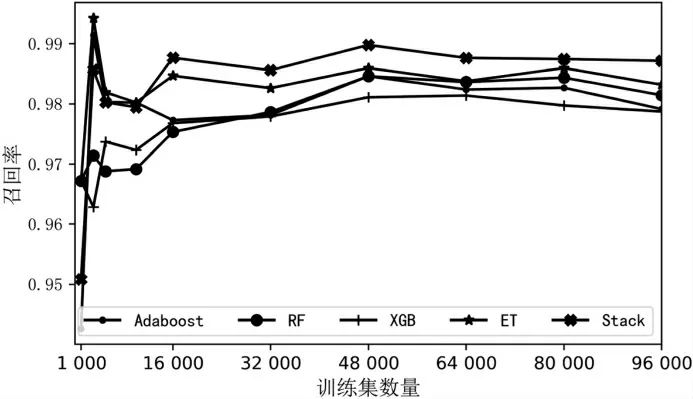
图9 算法召回率

在实际应用中，为了评价模型的综合性能，引入了F1 指标对模型进行进一步评判。F1 指标是精确率和召回率的调和平均值，F1 指标越高，说明模型更稳健。在图10 中可看出，在样本数量较大或较小的情况下，Stacking 算法的F1 指标均高于其他算法，故Stacking 模型融合算法具有更好的稳健性。

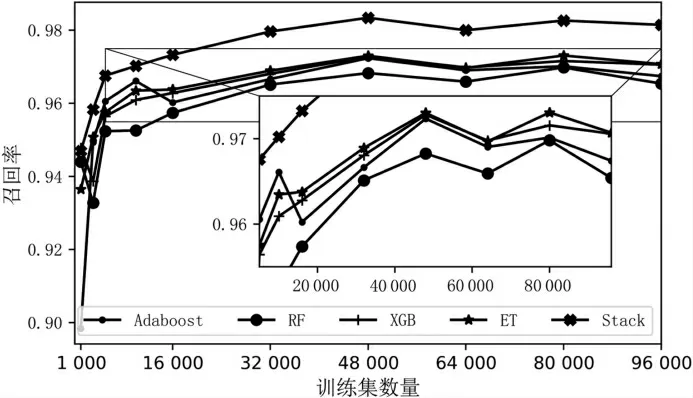
图10 算法F1 指标

综上所述，Stacking 模型融合算法不论在准确性、精确性、召回率以及F1 指标都有较好的表现，Stacking 算法更适合于故障电弧检测。

4 结论

本文主要针对住宅和配电网情况下的低压交流故障电弧检测，在此供电条件下，使用符合标准的故障电弧发生器采集电流信息。由于时频转换算法需要耗费大量计算时间，故本文只使用时域特征组成特征矩阵，结合模型融合进行故障识别。经过大量实验数据的验证可知，Bagging 集成框架和Boosting 集成框架对故障识别算法均有改进。但是将上述集成算法作为Stacking 模型融合的初级学习器进行故障检测可获得更好的性能。