基于组合模型的风电功率预测方法研究

王春梅

（国网冀北电力有限公司技能培训中心，河北 保定 071051）

0 引言

风能是一种无污染的清洁可再生能源，大力发展风电是解决环境污染和能源危机问题的关键举措之一［1］。风能随机性、波动性的特征增加了风电并网成本，同时影响电力系统运行的稳定性，因此提高风电功率预测准确性至关重要。

为解决风电功率预测问题，文献［2］提出多气象变量的模型组合预测方法，利用气象数据预测风电趋势，同时局部采用多变量模型改善预测精度，从而实现风电功率中长期预测。文献［3］提出灰色预测模型，利用历史风速数据资料和风电机组装机容量建立风速-功率函数来预测中长期风力发电容量。文献［4］提出粗糙集神经网络模型，利用粗糙理论分析出影响风速的主要因素作为神经网络预测模型的附加输入，实现风电功率中长期预测。以上文献采用不同的方法实现了风电功率中长期预测，其中多气象变量预测模型只考虑气象数据，但无法保证同一地点相同时间段的气象数据相同；灰色预测模型以历史风速数据资料为依据建立风速-功率函数，未考虑其他气象变量对风电功率的干扰；粗糙集神经网络模型考虑到影响风电功率的主要因素，但未考虑历史风电功率与当前风电功率的关系。

为解决上述问题，本文提出基于组合模型的风电功率预测方法。首先，利用灰色理论预测模型求得风电功率，以风速、温度、湿度、气压和求得的风电功率作为深度神经网络的输入建立组合模型；其次，分别用训练集训练模型，使模型参数最优；最后，分别利用测试集对模型进行仿真分析，并结合误差指标验证所提方法的有效性。

1 风电功率的影响因素

1.1 风电功率的主要影响因素

风力发电的基本原理是利用风推动桨叶旋转带动发电机，从而将风能转化为电能［5］。风电机组的输出功率为：

式中：P为风电机组的输出功率；Cp为风轮的功率系数；ρ为空气密度；A为风轮扫掠面积；ν为风速。对某一特定的风电机组而言，Cp、A和ρ可视为定值，由式（1）可知，影响风电机组输出功率的主要因素为风速ν。风电功率与风速的立方成正比，风速越大，风电功率越大，反之亦然。因而本文以风速作为风电功率的主要影响因素。

1.2 气象因素对风电功率的影响

影响风速的主要因素包括地形因素和气象因素。地形因素以地貌、地表障碍为主，气象因素以气压、气温和湿度为主［6］。风速与本地区和相邻地区的各气象因素均密切相关，且是复杂的非线性关系，因此只可做相关性分析不能利用数学函数描述。本文以某风电场2019年的历史风电数据为例进行相关性分析。2019年3月某风电场连续15日的风速及气象数据如表1所示。

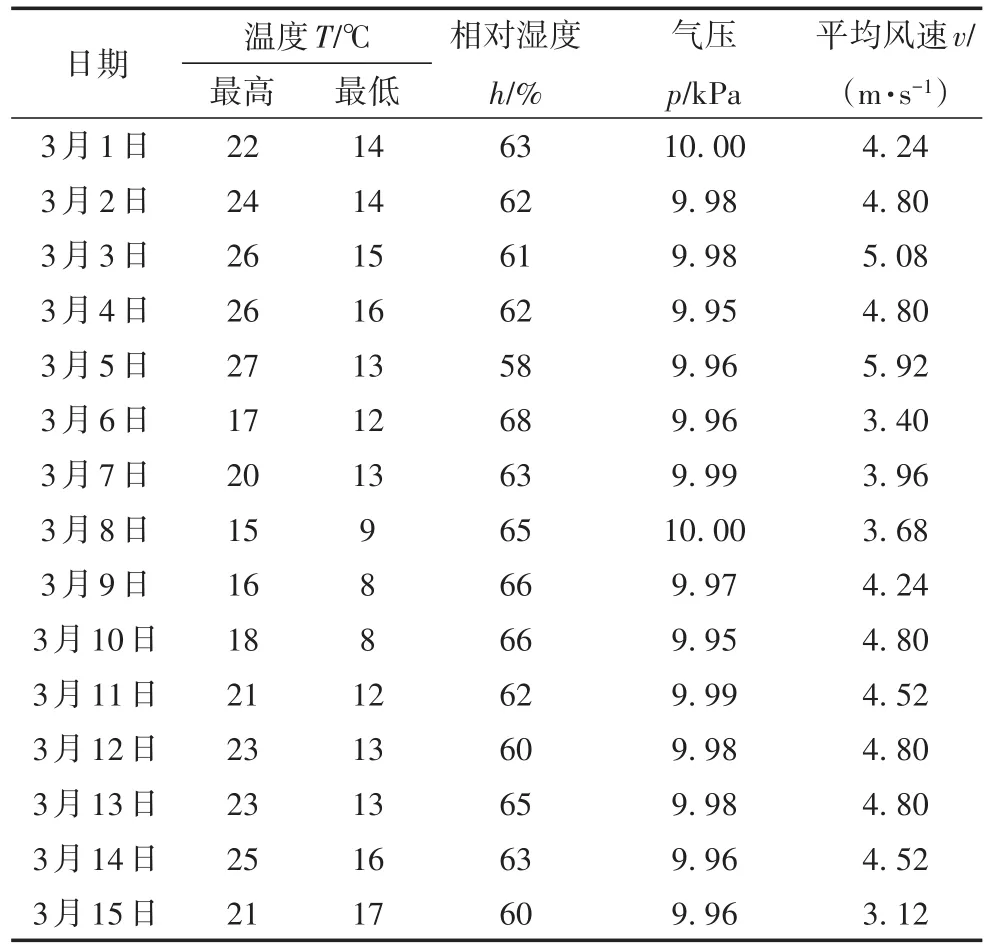
表1 某风电场3月份连续15日的风速及气象数据

由表1可见，相同的湿度和气压条件下，温度差越大风速变化越大；相同的温度和湿度条件下，气压的变化对风速的变化影响较小；相同的温度和气压条件下，湿度变化对风速变化影响相对较小。

2 风电功率组合预测模型

2.1 灰色理论模型

根据灰色理论模型，将已知风电功率历史数据进行累加后生成具有指数增长的新序列，利用微分方程拟合，从而对风电功率累加的预测值累减后得到实际功率预测值［7］。灰色模型（Grey Model，简称GM），用GM（1，1）表示。已知风电功率历史数据序列如下：

对序列X（0）进行累加生成新的序列

用式（3）生成紧邻均值序列Z(1)

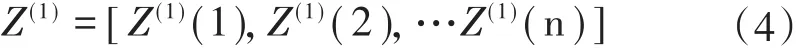
建立GM（1，1）模型的一阶白化微分方程

式中：a和b为参数［7-8］。将参数a和b代入式（5）中，令x(1)(0)=x(0)(0)，解微分方程可得到GM（1，1）模型为：

对式（6）作一次累减还原，得到原始序列X(0)的GM（1，1）预测模型为：

2.2 深度置信网络

深度置信网络（Deep Belief Network，简称DBN）能够对数据进行深度挖掘来提取重要信息和关键特征，由多个受限玻尔兹曼机（Restricted Boltzmann Machine，简称RBM）逐层叠加形成深层网络结构。DBN网络采用逐层贪婪算法优化神经网络连接权重，其模型训练步骤分为预训练和参数优化［8］。

1）预训练。通过依次把上一层RBM隐含层的输出作为下一层RBM可见层的输入，得到每层RBM的初始参数从而完成RBM各层逐层训练的过程。为加速RBM网络的训练速度，同时降低训练过程中的振荡，本文采用权值动量和对比散度（Contrastive Divergence，简称CD）算法相结合的参数更新公式：

式中：l为RBM的数量；m(l)为第l个RBM中的附加动量；η(l)为第l个RBM训练时的学习率。

2）参数优化。每层RBM网络参数最优无法保证DBN网络整体性能最优，因此需要进行参数优化以确保整体参数最优。将反向误差自顶向下传播逐步微调网络权值，反向参数优化各层网络权值更新公式：

式中：w(t)为DBN层间的权重；m(t)为DBN层间的附加动量；η(t)为DBN层间的学习率。

2.3 风电功率预测组合模型

中长期风电功率组合预测模型以风电场历史数据和气象数据例如风速、温度、气压和湿度为基础，弥补了灰色理论模型和深度置信网络模型的不足。首先以风电功率历史数据训练集训练灰色理论模型，同时将灰色理论模型的输出作为深度置信网络模型的输入；其次用测试集中气象数据和灰色理论模型的输出来训练深度置信网络，直至网络模型整体参数最优；最后用测试集验证模型性能。其中，深度置信网络由3个RBM网络层和单层BP网络构成，RBM的输出端连接Softmax函数进行多分类，BP网络层作为深度置信网络的输出层。风电功率组合预测模型结构如图1所示。

图1 风电功率组合预测模型结构图

3 实例仿真与分析

本文取某风电场2019年采样间隔1 h的风电功率数据和相应气象数据例如温度、湿度、气压和平均风速作为风电样本数据。其中，1—6月份的数据作为训练集，用于训练组合模型使其参数最优；7—12月份的数据作为测试集，用于模型评估和风电功率预测。

3.1 风电功率预测

由深度置信网络模型训练步骤可知，模型训练分为预训练和参数优化两步［9］，具体如下：①采集功率的历史数据和气象数据如风速、气压、温度和湿度，并对数据进行预处理，划分测试集和训练集，设置标签并进行归一化处理。②确定网络参数，包括学习率、附加动量、迭代次数、隐含层数和各层节点数等。③将当前隐含层的输出作为下层隐含层的输入，得到每层的权重和偏置最优时的参数值，通过逐层训练从而达到局部性能最优。④采用BP算法反向微调参数，通过反向微调使最初的权重和偏置参数达到全局性能最优。⑤判断当前准确率是否达到要求，若满足则训练结束，否则重复步骤③和步骤④。

深度置信网络性能与所选参数有关，为获得最优参数采用网格化搜索技术［10］来确定最优学习率η及惯量参数m。其中，m从0.1到0.6，每隔0.1取一个值；学习率 η 分别取 1×10-2，5×10-3，1×10-3，5×10-4，1 × 10-4，5 × 10-5，1 × 10-5。每种参数配置下的平均准确率如图2所示。

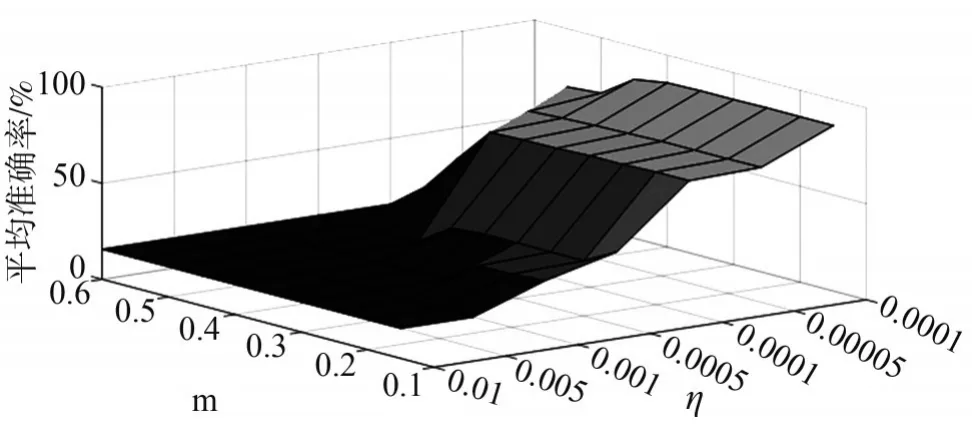
图2 不同参数配置下的准确率

由图2可见，不同的参数配置对算法性能有较大的影响，根据仿真结果可知，当学习率η=1×10-5，惯量参数m=0.3时，平均测试准确率为86.18%，DBN网络性能达到最优。因此，选择η=1×10-5，m=0.3。

为验证中长期风电功率组合模型预测方法的准确性和高效性，在相同的训练集和测试集条件下，与中长期风电功率灰色理论模型和BP神经网络模型预测方法进行对比试验。风电功率预测结果如图3所示。

图3 风电功率预测结果

3.2 误差分析

为定量分析风电功率组合模型预测方法，本文采用传统误差指标进行对比分析。误差指标分为纵向误差和横向误差两类，纵向误差是从宏观角度分析预测系统长期运行状态，横向误差则从时间角度研究预测系统的性能［11-12］。分析预测结果时，纵向误差为绝对值平均误差（Mean Absolute Error，简称MAE）、均方根误差（Root Mean Squared Error，简称RMSE），横向误差为相关系数（Correlation Coefficient，简称CC）。将纵向误差和横向误差作为预测模型性能评估指标，各误差指标表达式为：

式中：xi表示实测数据点；x^i表示预测数据点；n表示预测样本数。风电功率预测结果误差分析如表2所示。

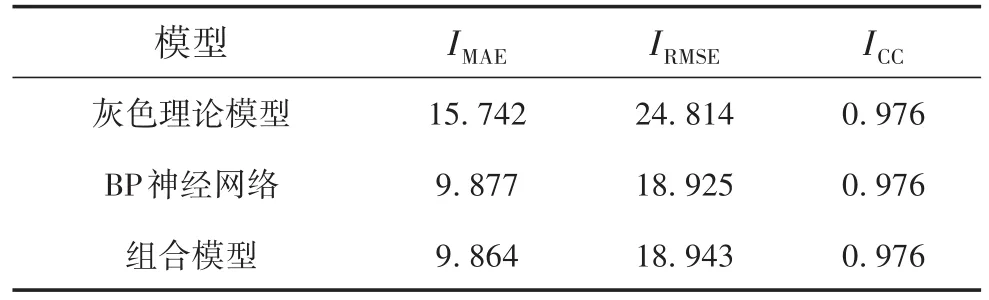
表2 风电功率预测结果误差分析

对比分析表2中的结果，由IMAE和IRMSE的评估值可知，采用组合模型的风电预测结果与实际观测值间的误差较小，与图3中的直观分析相符。由ICC指标可见，组合模型的横向误差变化较小。从横向误差分析可知，由于多模型优化组合考虑了NWP提供气象信息，因此预测结果的时间延迟较小且改善不大，即ICC值接近1。

由图3定性分析和表2定量分析可知，与灰色理论模型和BP神经网络模型相比，中长期风电功率组合模型预测结果精度较高。

4 结语

本文结合灰色理论模型和深度置信网络模型的优势，提出中长期风电功率组合模型预测方法。以某风电场的风电功率数据和气象数据如风速、温度、气压和湿度为数据样本，将灰色理论模型的输出作为深度置信网络的输入，实现了较高精度的中长期风电功率预测。通过与灰色理论模型、BP神经网络风电功率预测方法对比分析，进一步验证了所提方法的有效性。