基于CT扫描的草炭土孔隙结构分析及渗流模拟*

杨圣涛 吕 岩 贺元源 刘婷婷 马晓祯

(吉林大学建设工程学院， 长春 130026， 中国)

0 引 言

草炭土主要分布于我国的东北、西南、长江中下游地区(佴磊等， 2012)，主要发育在地表低洼，积水较多的沼泽类环境。草炭土是植物残体经氧化和不完全分解作用堆积而成的一种特殊的腐殖质土，具有特殊的物质组成与结构特征，在自然环境状态下，草炭土表现出高渗透性、高孔隙比、高含水量等不良工程地质特性(徐燕等， 2011)。近年来，修建在草炭土分布区的路基大多出现了不均匀沉降的现象，这些现象的存在影响了当地建筑工程的安全性、线路工程的交通营运(刘飞， 2011)。引起不均匀沉降的因素之一便是草炭土的高渗透特性，与其他黏性软土相比，草炭土中的有机质含量高，土体内部布满了植物纤维，因而孔隙发育，从外部表现出疏松多孔的形态。草炭土的分解度与有机质含量与其高渗透性紧密相关，毛文飞(2015)、汪之凡等(2017)通过室内试验，对吉林省靖宇县采取的草炭土样的渗透性的影响因素以及影响规律进行了较为全面的分析，认为草炭土的分解度和有机质含量对草炭土的渗透性产生影响，且分解度的影响更为显著，渗透率随着分解度的增大而降低。

近年来，CT扫描技术在岩土体的微观结构研究方面越来越广泛。CT扫描技术是一种无损的成像技术，能够探测材料内部的几何形态，相比于其他试验方法，CT技术适用于在不破坏岩土体孔隙结构的情况下获取到岩土体的细观结构图像，进而通过三维重构技术实现对岩土体的三维形态的研究。诸多学者运用CT扫描技术来开展对岩土体结构的三维重构进而深入研究。张标等(2021)通过CT扫描技术并使用Avizo重构了珊瑚骨架灰岩的三维数字孔隙模型，毛伟泽等(2020)基于CT扫描技术实现了对花岗岩矿物颗粒三值化的三维重构。Mimics为比利时Materialise公司开发的面向医学影像技术的专业3D建模软件(苏奎等， 2020)。作为专业的医用影像建模软件，Mimics支持多种无损压缩的格式图片的导入，且Mimics具有成熟的三维尺度上的体积计算功能，适用于CT扫描序列图像上的信息识别以及重构三维模型(王娇等， 2015)。

此外，随着计算机技术的普及和发展，越来越多的学者基于CT扫描的图像在土体渗流数值模拟上完成了许多卓有成效的研究，宋帅兵(2020)分别基于有限元数值理论模型、孔隙网络模型计算得到高庙子膨润土的渗透率，并加以渗透率试验进行验证，认为CT 微米级模型和FIB/SEM纳米级模型分别具有最高和最低的渗透率数值。

Lattice Blotzmann方法是20世纪80年代发展而来的介于微观分子动力学和宏观连续介质模型之间的介观模拟方法，在多孔介质渗流的模拟方面具有独特的理论性。昆明理工大学申林方、王志良等人(申林方等， 2014，2015； 侯汝几等， 2015； 崔冠哲等， 2016； 王志良等， 2018))采用D2Q9模型运用格子Boltzmann方法对二维平面的二值图像进行数值模拟并研究了土体渗流场的变化机制。此外，国外的研究人员以LBM理论研发了PALABOS代码库(Latt et al.，2021)，能够模拟解决各种不同环境下的流体流动问题(Huang et al.，2015)。在代码库的基础上修改其多孔介质的流动模拟程序能够实现对岩、土体内部孔隙的渗流模拟。

本文以吉林省敦化市的草炭土为研究对象，通过CT扫描试验获取草炭土的切片断层图像。通过Mimics21.0体积计算的孔隙率结合真实孔隙率对比确定草炭土CT图像的二值化的最优阈值。基于草炭土的重构三维模型以及序列CT图像的横截面与纵截面分析了草炭土的内部的孔隙形态。从LBM的基本理论出发，通过改编程序对草炭土CT序列图像进行单相BGK渗流模拟，研究了LBM理论下草炭土的渗透率以及其内部流线与流速的分布。基于以上这些研究内容，本研究能够作为草炭土或软土渗流模型研究的理论基础，可以指导这些地区的工程建设。

1 试验方法

1.1 样品的采集

草炭土样品采集自吉林省敦化市江源镇地区地表下的典型草炭土层。为了获取不受扰动的草炭土试样，试验坑被开挖至地面1.5m左右的深度，用内径为0.1m的PVC圆筒推切草炭土并将其包裹后取出(图1)。将取出的样品用黑色塑料袋与胶带进行二次密封处理，并标记土样编号，直接运送至实验室进行冷藏。冷藏期间保证冷藏室温度为3～5℃，防止样品中的植物纤维取出后再度被微生物分解。

图1 草炭土的现场样品

1.2 土体的基本物理性质指标

本文选取地表下1.05～1.20m深度内的3份草炭土样品，分别通过室内试验测得其土体的天然密度ρ，土粒密度ρs、天然含水率ω等基本物理指标，经式(1)、式(2)换算得到3份草炭土样的孔隙率n，如表1：

表1 草炭土的基本物理性质

(1)

(2)

1.3 CT扫描试验

本文进行CT扫描试验所用的仪器为比利时BRUKER-MICROCT公司生产的 Skyscan 1172 型桌面X射线CT系统，试验在中国科学院长春应用化学研究所完成。CT扫描的草炭土样品选择的是1.1中进行室内试验的同一批冷藏封存的3份样品，试样编号一一对应。试样尺寸是直径约8mm，高约10mm的圆柱体。将样品放置在真空冷冻干燥机内，在-45℃的条件下进行抽真空24h，使其内部的水分全部被蒸发。通过X射线穿透样品进行逐层扫描，便可以得到在不同角度方向该层面的“切片”投影图像(巩林贤， 2020)，并通过 Micro-CT扫描仪自带的容积重构软件Nrecon(V1.6.1.0)中的FDK重建算法处理“投影”图像，将投影图像转换成二维断层切片图像。

扫描后得到的二维断层切片图像的像素单元尺寸为5 μm，其能反映的最小孔隙直径为5μm。最小扫描层厚为7.5μm，经扫描及投影后得到草炭土3份土样的断层切片图像数目分别为1332张， 1324张， 1323张。二维断层图像的分辨率为2000×2000，图片格式为8位位图的BMP格式，能够无损且颜色准确地保留图像信息。

2 草炭土CT序列图像的二值化最优阈值选取及三维模型分析

2.1 CT图像的预处理

在采集草炭土样品的CT图像的过程中，在草炭土的侧边加上了固定环圈防止扫描过程中草炭土自身发生扰动，因而在二维断层切片图像中草炭土的周边显现出固定环圈的痕迹。同时，由于设备运行过程中，因电压不稳造成图像局部灰度失衡，出现细小的斑点，使得图像信息失真(赵玥等， 2018)。为了消除以上原因对图像信息产生的干扰，本文采用MATLAB分别对原图像进行裁剪； 利用中值滤波法进行图像去噪处理，处理前后效果见图2。

图2 图像的预处理

经过程序处理的图像，像素大小由原图像的2000×2000裁剪为1100×1100，消除了图像中交织的噪声，使得肉眼能够更清晰地分辨出孔隙与土颗粒的信息。

2.2 CT图像的二值化的最优阈值选取

2.2.1 二值化最优阈值选取的方法

Mimics中能够通过阈值(Threshold value)划分得到该灰度值区间下的蒙罩(Mask)，蒙罩部分能够快速且准确地计算蒙罩体积(Mask volume)。通过调整阈值形成各个部分的灰度值区间，生成并查看mask部分的属性(Properties)能够得到各个部分体积计算的结果，从而确定各个部分的体积大小。通过计算V孔隙mask/(V土颗粒mask+V孔隙mask)能够得到Mimics计算的CT序列图像的孔隙率。

本文使用阈值分割的方法进行CT图像的二值化。采用试凑法，结合室内试验换算得到的草炭土样品的真实孔隙率与Mimics的体积计算功能，通过调整土颗粒与孔隙的阈值形成各自的灰度值区间并生成蒙罩，分别计算不同阈值下的孔隙率。当样品的真实孔隙率与Mimics计算得到的孔隙率一致时，以该阈值作为最优阈值，进行图像的二值化，以保证后续图像信息转换的准确性。

2.2.2 二值最优阈值的确定

将预处理完毕后的草炭土样品CT序列图像导入至Mimics 21.0的工作区间上，在轴断面(Axial)窗口中，使用某条直径做剖面线(Profile Line)进行灰度值提取，见图3。

图3 草炭土CT图像剖面线

不同的介质由于密度不同，灰度值存在差异，能够通过灰度值的大小来进行定量识别。从图4可见，当剖面线经过孔隙部分时，灰度值位于0～80之间，波谷处呈锯齿状波动； 当剖面线经过土颗粒部分时灰度值明显上升，位于60～200之间，曲线波动幅度小。分析得出，由于孔隙的边缘不明显，在灰度值位于60～80之间时，像素点的位置既有可能是孔隙部分也有可能是土颗粒部分。此外，当剖面线经过土颗粒中夹带的矿物质时，出现明显的波峰，灰度位于约150以上，矿物质颗粒越大越明显，灰度波峰越高。

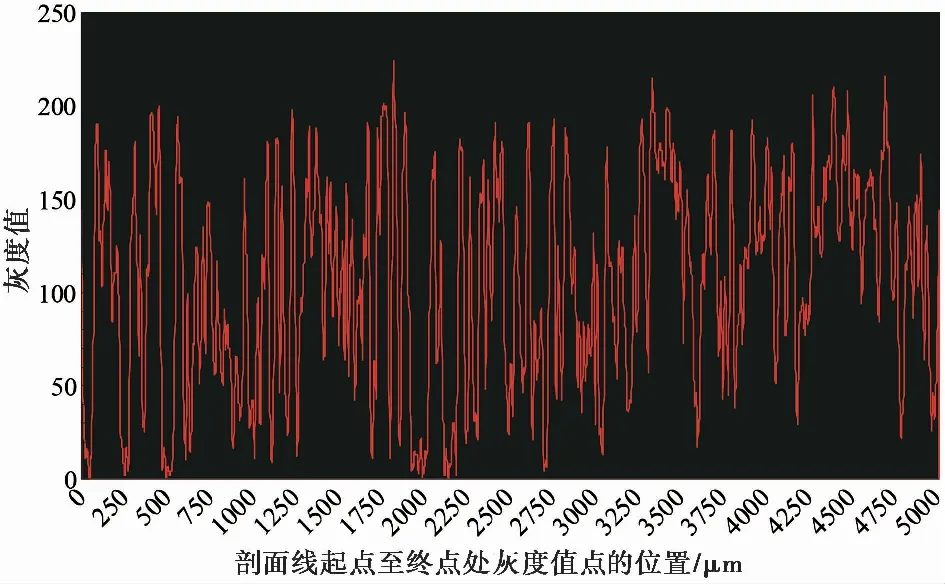
图4 剖面线土颗粒、孔隙、矿物质灰度值分布图

本文分别计算了土颗粒与孔隙的阈值为60～80下的孔隙率，得到阈值大小与土体孔隙率关系曲线，并结合室内试验换算得到的同一深度下的3份草炭土样品的真实孔隙率，投射至关系曲线上，如图5所示。

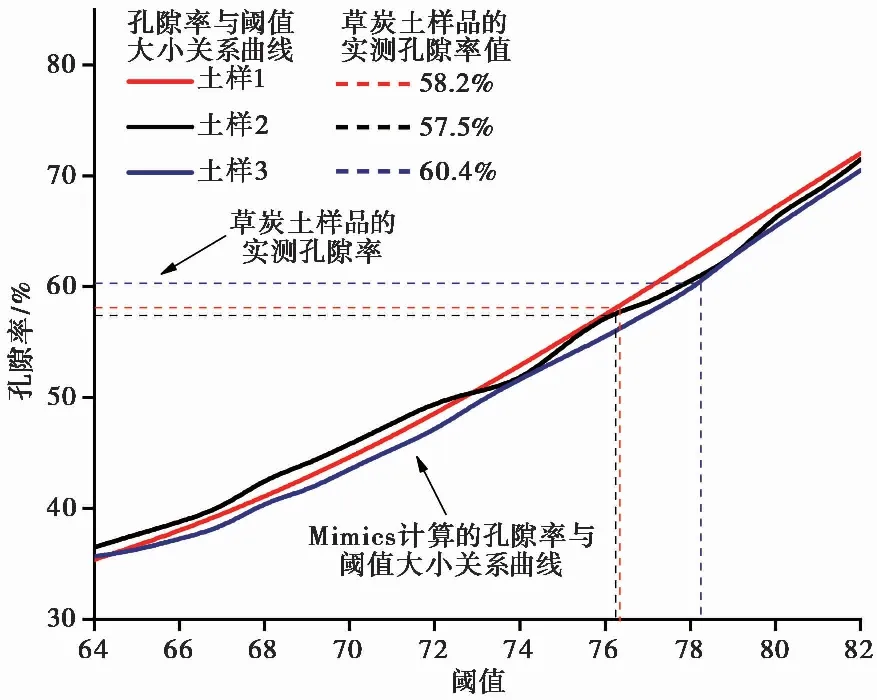
图5 土体真实孔隙率对应的阈值

由图5可知，本文将76作为土样1与土样2 CT图像的最优阈值， 78作为土样3的最优阈值。

2.2.3 二值化处理

在得到图像的二值最优阈值后，采用MATLAB编程进行图像的二值化，效果如图6所示。

图6 二值化效果

经过选取最优的阈值进行图像分割后，草炭土的CT图像分成了孔隙与土颗粒两部分，分割的效果较好，能够完整地提取图像中的信息，为后续草炭土的渗流模拟研究提供精确信息。

2.3 草炭土CT序列图像的三维模型与分析

在Mimics 21.0的工作区间上将阈值区间划分为土颗粒，矿物质颗粒和孔隙3个部分。将每部分存放于各自的Mask内之后利用腔隙填充(Cavity fill)、编辑蒙罩(Edit masks)等方法修改蒙罩中的像素，编辑处理完成后经3D Calculate得到各个部分较为精确的三维结构模型，组合后便得到了完整的草炭土三维重构模型，如图7所示。

图7 草炭土三维重构模型

基于三维重构模型，能够获得土颗粒、孔隙、矿物质的空间分布规律。从图上可以看出，草炭土中的土颗粒与孔隙之间交互分布，矿物质颗粒均匀地分布在土颗粒中。孔隙散乱地分布于模型的各个区域，孔径大小不一，大孔径与细孔径的孔隙形态各异，大孔径孔隙的贯通性良好，而细孔径的孔隙则散布于各个区域。CT序列图像的横截面与纵截面图像上能够清楚地看见大孔径孔隙的形态，如图8所示。草炭土的土颗粒部分为有机质并夹杂有植物纤维，植物纤维在有机质中呈条状分布，从图中也能看出从植物纤维夹有长条状或圆管状的植物孔隙。结合三维模型与截面图像能够发现，植物纤维在土中呈现架空状的结构也会形成大孔径孔隙，草炭土孔隙的形成受到植物纤维分布的影响，因此孔隙结构与植物纤维的含量和分解度紧密相关。

图8 植物纤维形成的根管状孔隙

3 草炭土CT序列图像的渗流模拟

3.1 LBM的基本原理

Lattice Boltzmann Method(LBM)基于Boltzmann于1872年从分子运动论和统计物理的理论推导出来Boltzmann方程，从微观动力学角度出发，将流体连续介质看作大量位于网格节点上的离散流体质点粒子(何雅玲等， 2009)。粒子按碰撞和迁移规则在网格上运动，通过对各网格流体质点及运动特征进行统计分析，获得流体宏观运动规律。LBM完整的格子模型由分布函数的演化方程、离散速度模型、平衡态分布函数3部分组成(杨佳庆， 2010)。

本文使用Qian et al.(1992)提出的D3Q19模型，为了估算碰撞项，这里运用BGK(Bhatnagar-Gross-Krook)动力学对碰撞项进行线性化的处理，BGK单相松弛LBM模型中松弛时间τ由单个参数定义，以此来实现对Navier-Stokes方程的求解(Mandzhieva， 2017)。模型的粒子分布函数如式(3)所示：

fi(x，t)-fi(x+eiδt，t+Δt)=

(3)

式中：τ为松弛时间(粒子碰撞速率)，与流体的黏度有关； δt为离散时间步长；fi(x，t)为平衡粒子分布函数。方程左边表示的是粒子的流动，粒子在每个方向将离散速度的传递至各自相邻的节点； 方程右边表示的是粒子间的碰撞出现的平衡粒子分布的一部分松弛效应。

D3Q19的空间离散速度为图9所示。

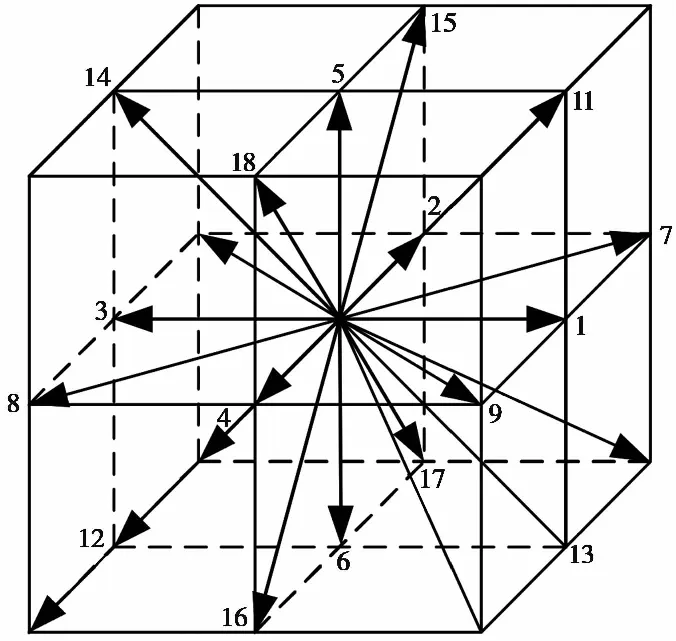
图9 D3Q19模型

D3Q19模型中平衡态分布函数表示为：

(4)

式中：ρ为密度；cs为格子声速；ωi为权系数；u为流体的宏观平均流速；ei为粒子的离散速度。

D3Q19模型中格子声速cs以及权系数ωi分别为：

(5)

(6)

粒子的离散速度ei的大小由格子速度决定，格子速度c=δx/δt，δx为格子步长。

BGK单相松弛LBM模型存在着的渗透率会随松弛频率的增加几乎呈现线性增加的状态，但是当c=1时能够避免这一非物理现象(Mandzhieva， 2017)。因此本研究选择δx=δt，使得c=δx/δt=1，从而实现在细观尺度下由Lattice Blotzmann方程来替代Navier-Stokes方程。

因而，流体的宏观流动特性可以由细观上的每个时间步的分布函数近似得到，如式(7)，式(8)所示：

(7)

(8)

式中：ρ为模型的宏观密度；u为模型的宏观速度。

3.2 模型边界条件的处理

在渗流问题的模型的设置上，边界条件一直都对数值模拟的结果起着至关重要的作用(周潇， 2016)。结合本研究问题，采用周期性边界与反弹边界进行数值模型的边界条件处理。设定草炭土模型的流体出入口采用周期性边界格式，不透水边界以及草炭土颗粒采用反弹格式。

3.2.1 反弹格式边界

反弹格式假设粒子与土颗粒表面以及壁面发生碰撞，碰撞后粒子速度发生逆转，速度大小不变，朝着相反的方向发生反弹，反弹格式边界处粒子的运移方式如图10所示。

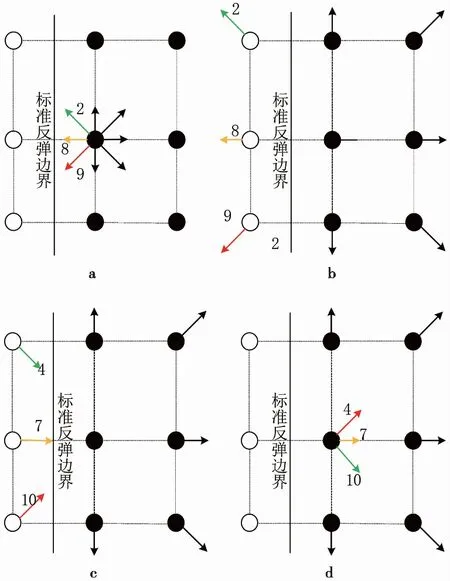
图10 反弹格式边界处流体粒子运移的4个阶段

流体粒子迁移到边界处，速度发生逆转，碰撞后粒子沿原路返回，在图10中发生的碰撞分布函数为：

f2， 8， 9(i，l)=f4， 7， 10(i，l)

(9)

3.2.2 周期性边界

设置上下边界为周期性边界条件，假设计算域的出口的流体再次从入口流入，保证在非稳态与周期性的出入口边界条件下使得渗流模拟的过程趋于稳定，最终的计算结果得到收敛，计算得到草炭土的渗透率。

3.3 程序的编制

3.3.1 基于MATLAB的图像信息转换程序

通过MATLAB中的imread函数功能，自编程序读取CT序列图像的信息，提取图像数据并转化成数据结构。数据结构包含序列图像各个像素点的索引值，储存在代码能够读取的二进制(.dat)文件中。程序设定的数据结构表示：

B(i，j，numFiles)=

(10)

式中：i，j表示的是图像中像素单元的位置；numFiles表示的是图像的序列号。

3.3.2 基于LBM的渗流模拟程序

渗流模拟程序基于PALABOS开源代码库(https：∥palabos.unige.ch/)，采用C++语言依照以上基本理论编制了草炭土渗流的计算程序。根据构建的数据结构表征的数值，在程序中规定：流体粒子在读取到值为0的体素中正常迁移，值为1的体素速度发生反弹，值为2的体素中被设定为无法迁移。出入口两端设置固定的压差，模拟流体在孔隙内线性流动，当相邻时间步长的速度变化量小于收敛值，则判定流体的运移达到稳定状态，停止模拟。

3.3.3 程序中渗透率的计算与单位转换

本研究中模拟是水这一不可压缩流体在孔隙内的流动。程序基于达西定律由流体粒子的流速计算求解土体的渗透率，关系式如下：

(11)

在格子单位领域渗透率是以无量纲单位输出的，使用式(12)将其转换为物理单位。

(12)

式中：Lphysical等于图像分辨率与像素单元大小的乘积；LPALABOS等于格子单位的长度。

3.4 草炭土CT序列图像的细观渗流模拟

3.4.1 CT序列图像的选取

由于LBM模型无法完整地读取圆形切片图像上的信息，因此在渗流模拟的研究中重新从原始图像中裁剪出方形区域，并对图像进行预处理、二值化。选取处理后的草炭土CT切片图像中连续的814张图像，将序列图像转化为二进制的信息文件。草炭土整体的序列图像如图11所示：

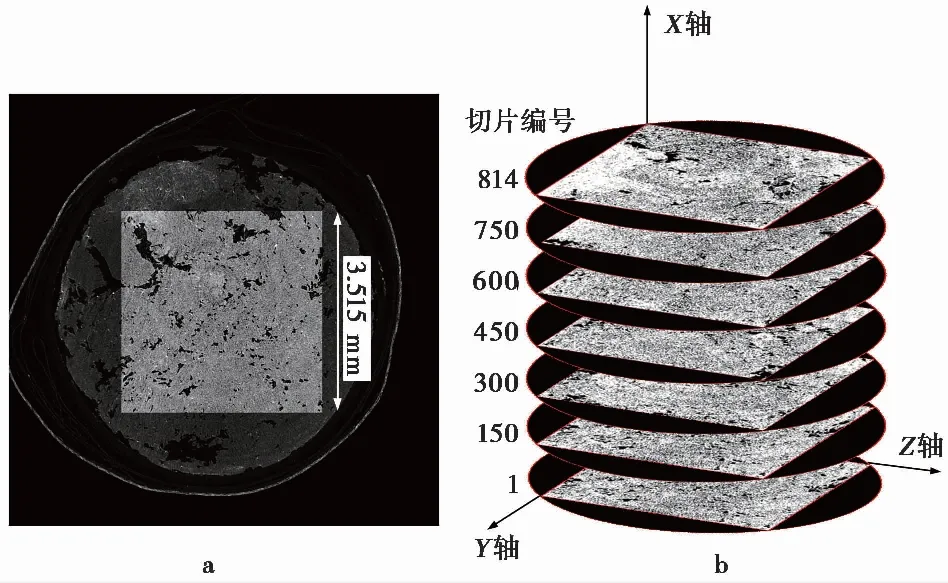
图11 草炭土方形CT序列图像示意图

3.4.2 模拟初始条件的设定

模型模拟设定的初始条件见表2。

表2 模拟的初始条件

3.4.3 模拟结果分析

3.4.3.1 数值模拟的草炭土的渗透率结果

基于上述模拟过程分别测得3份草炭土样品的渗透率，结果如表3所示。

表3 格子单位与物理单位下计算的渗透率

本文得到基于LBM理论下3份土样的模拟渗透率值。通过与文献对比发现，基于LBM法计算得到的草炭土的渗透率与Avizo软件的X-lab算法(巩林贤， 2020)以及实验室实测(汪之凡等， 2017)的渗透率值接近，说明基于LBM理论的模拟结果具有一定的可靠性。

3.4.3.2 流速云图与流线图的分析

本文结合Paraview可视化软件，将模拟得到土样1的VTI格式文件导入至Paraview中进行可视化。得到图12草炭土渗流路径云图，图13为不同数量位移积点的流速流线分布图。从流速云图上我们可以看出，草炭土的孔隙分布复杂，孔隙孔径大小不一，大孔径的贯通性优于散布的细孔径孔隙，存在着大孔径渗流通道。在土体渗流稳定后，流体流动的方向优先选择连通性良好的孔隙所形成的通道。

图12 土样1孔隙内部的渗流路径云图(上方入，下方出)

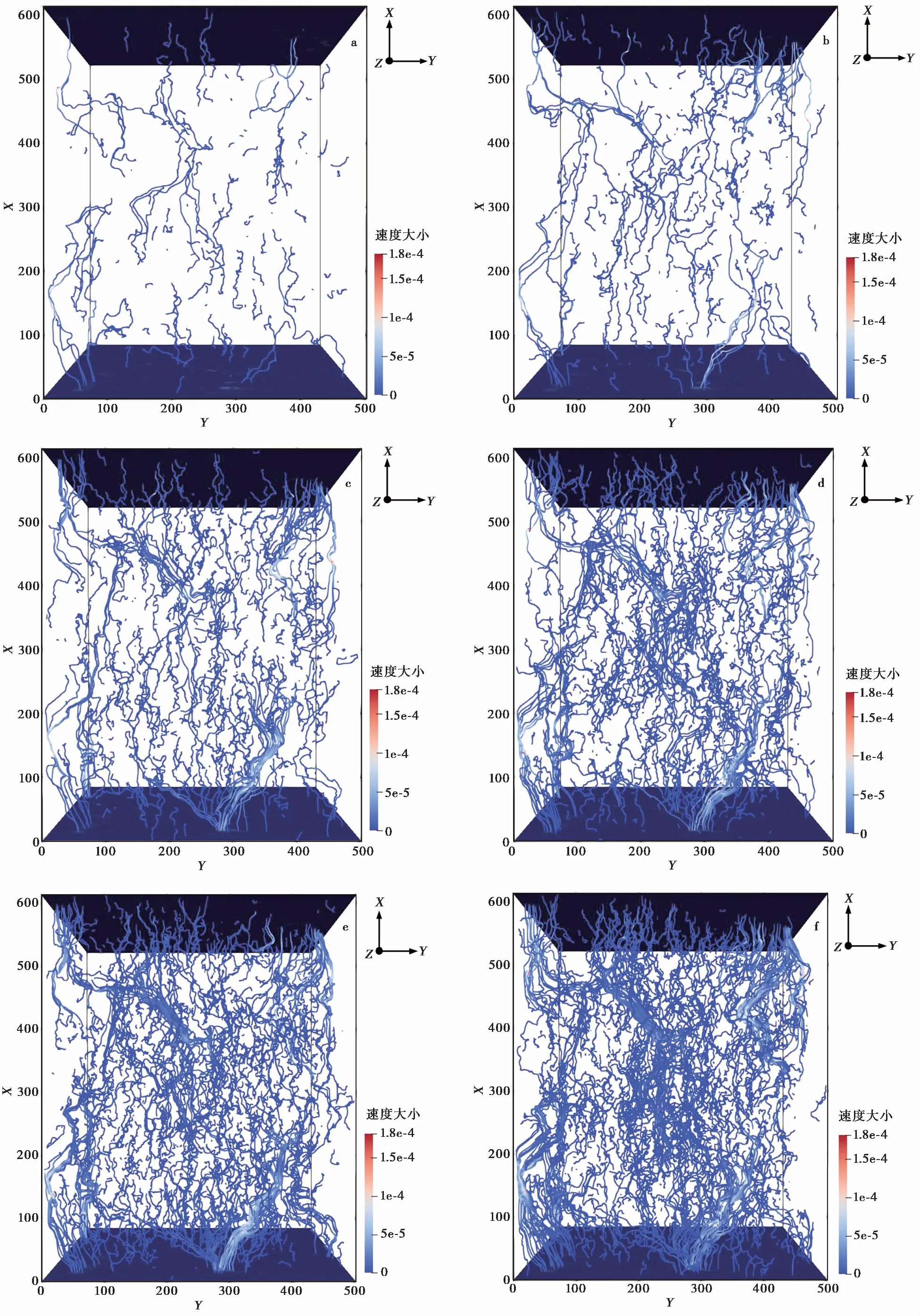
图13 土样1孔隙内部的流线分布图

草炭土的孔隙内部的流线分布图中，Number of Points是指位移积点的数目。结合流速云图我们可以看出，从Number of Points=1000～10000的过程中，位移积点的位置越来越集中于贯通的大孔径孔隙。大孔径孔隙内的流线数目越来越多，而部分连通的孔隙散布着细小的流线。说明大孔径内的流线数目多于其余不贯通孔隙，进一步表明了大孔径孔隙是草炭土渗流的主要通道，对草炭土的渗透性起着至关重要的作用。

3.4.3.3 流速的变化分析

本文分别从流速云图XZ截面(Y=314处)上选取Z=381与Z=240两条X向(竖向)截面截线(图14)以及XY截面(Z=237处)上选取Y=229与Y=414两条X向(竖向)截面截线(图15)，提取截面截线上的流速信息并绘制流速分布曲线。

从流速云图(图14a、图15a)中可以看出，大孔径孔隙内流体渗流量大，流速明显高于不贯通的细孔径孔隙。结合流速分布曲线(图14b、图15b)可知大孔径孔隙通道出现了整个流域内最大的渗流速度，这些大孔径孔隙之间互相贯通，流体在其中的流通性非常好； 而部分连通的孔隙不存在较大的流速，流体在其中流动断断续续，这也是由于草炭土土体孔隙复杂，水在不贯通孔隙流动的过程中能量被消耗，流速逐渐减缓。

图14 土样1 XZ纵截面上的代表性截线流速

图15 土样1 XY纵截面上的代表性截线流速

由此可见土体的孔隙结构尤其是大孔径孔隙的数量在一定程度上影响着草炭土的渗流特性。而大孔径孔隙的分布与土中植物纤维的分布有关，因而草炭土的渗透率受到植物纤维的含量以及分解度影响，植物纤维的含量越多，越分解不完全，草炭土内部越架空，内部的孔隙贯通性越好，渗透率越高； 反之，则渗透率越低。

4 结 论

(1)本文采用试凑法，通过Mimics21.0的Mask体积计算功能得到草炭土CT序列图像的孔隙率，结合土体真实孔隙率，得到了3份样品图像二值化处理的最优阈值为76， 76， 78。该方法确定的CT图像二值最优阈值能够精确地提供图像提取的信息。

(2)基于三维重构模型并结合CT序列图像的横截面与纵截面发现草炭土的孔隙结构复杂，孔径的大小不一，孔隙形态各异，植物纤维形成的圆管状孔隙通道以及架空状孔隙结构是大孔径孔隙形成的主要原因。因此土体内部大孔径孔隙的分布与植物纤维的分布紧密相关，植物纤维形成的大孔径孔隙会成为草炭土渗流的优先路径。

(3)基于LBM理论，采用C++算法改编程序，在细观尺度上对草炭土的孔隙进行单相BGK渗流模拟，计算了草炭土的格子单位下的渗透率，并转化为物理单位下的渗透率，计算得到3份土样的渗透率分别为7.1358 μm2、5.5194μm2、6.713675μm2。通过与以往的文献数据对比发现LBM算法的结果与Avizo的X-lab算法以及实验室实测值的渗透率值接近，说明基于LBM理论的模拟结果具有一定的可靠性。

(4)通过Paraview可视化的渗流路径云图、流线分布图、以及代表性截线流速曲线分析发现，在细观尺度上草炭土内的流体优先选择大孔径的渗流通道，流线大都集中于这些大孔径的孔隙中，而部分连通的孔隙散布着细小的流线。大孔径孔隙通道内出现了整个流域内最大的渗流速度。细孔径孔隙内不存在较大的流速，流体在其中流动断断续续，能量消耗快于大孔径孔隙，流速逐渐减缓。说明草炭土的孔隙结构尤其是大孔径孔隙的数量会影响土体的渗透性。而孔隙结构与植物纤维的含量以及分解程度有关，因而土体中的植物纤维的含量以及分解度会影响土体的渗透性，植物纤维的含量越多，分解度越低，草炭土的渗透率越高，反之则越低。