基于PFC3D 的黄土三轴试验细观参数敏感性分析*

许江波 曹宝花 余洋林 骆永震

(长安大学公路学院， 西安 710064， 中国)

0 引 言

黄土作为一种第四纪的松散堆积物，广泛分布于中国西北、华北地区，其抗剪强度是表征黄土工程地质条件最重要的特征之一，目前数值模拟试验是研究黄土特性的重要手段。由于PFC3D软件模拟三轴试验效果较好，并可从微观角度分析黄土试样试验过程中的应力变化特征，理论上试样的抗剪强度与土颗粒摩擦系数、孔隙率等密切相关，因此研究黄土三轴离散元细观参数对黄土宏观力学性能的敏感性影响是三维颗粒流PFC3D能否真实有效反映黄土实际特性的关键。

黄土三轴数值模拟细观参数的确定是一个复杂的过程，为获得与室内试验结果吻合度很高的细观参数值，需进行大量的试运算，所以对三轴试样进行细观参数敏感性分析是有效选择离散元细观参数值的前提。目前，部分学者基于颗粒流软件对不同类型土体细观参数进行了相关研究。砂土是一种无黏性土，为研究颗粒形态、颗粒粒径大小、摩擦系数、孔隙率等细观参数对其压缩性能的影响，一些学者开展了砂土试样颗粒流数值试验，发现颗粒粒径大小、孔隙率均能明显影响砂土的压缩特性(罗勇等， 2008； 乐天呈等， 2018； 郑博宁等， 2019)。很多研究人员通过对黏性土进行常规三轴试验模拟，探讨了离散元法在黏性土等领域的应用现状，揭示了颗粒流细观参数的变化对黏性土应力-应变曲线的影响，发现细观参数孔隙率、黏结强度、摩擦系数等细观参数能较大程度影响黏性土的宏观力学性质，并建立了颗粒流细观力学参数与宏观力学指标的关系(邢炜杰等， 2017； 彭国园等； 2017； 宁孝梁， 2017；程升等， 2018)。粗粒土是由大小不等的粗细颗粒组成，最大颗粒可达1000mm以上，最细可小于0.1mm，粒径变化范围很大，粗细颗粒特性相差悬殊，不同学者对粗粒土进行了室内三轴颗粒流模拟试验，发现影响模型试样宏观力学特性的细观参数也存在差异(Bagherzadeh-Khalkhali et al.，2009；刘勇等， 2014； 张志华， 2015)。除了利用常规三轴数值模拟试验研究细观参数对不同类型土体宏观力学特性的影响以外，国外部分学者也通过双轴压缩试验展开了细观参数对不同土体的敏感性分析，发现颗粒流颗粒形状对材料的压缩性影响显著(Williams et al.，1997； Pena et al.，2008； Utili et al.，2008)。李识博等(2013)针对陇西地区的黄土进行了CU细观数值模拟，结果显示颗粒刚度比控制泊松比，摩擦系数控制峰值强度，黏结强度对黄土试样黏聚力的影响较大。常晓林等(2012)基于PFC3D对堆石土体进行了常规三轴模拟试验，揭示离散元颗粒长短径比的变化能显著影响数值试样的峰值强度和残余强度，对模型试样的初始模量也有一定影响。国内学者也通过自主研发的离散元软件模拟滑坡滑移过程中产生的摩擦热对滑坡产生的影响，揭示了摩擦系数越小滑坡越容易产生滑动现象(郭政豪等， 2019； 朱晨光等， 2019)。

目前，部分学者基于颗粒流室内三轴数值试验的研究主要集中于对砂土、粗粒土等无黏性土力学性能规律性的研究，对于黄土类等具有黏聚力的材料虽然已建立相关模型并做了相关的研究，但目前这些研究主要局限于二维颗粒流PFC2D对土体进行平面双轴试验，并且对于加载过程中黄土三轴颗粒运动规律及细观参数的标定没有一致的结论，未借助PFC3D颗粒流软件系统地从细观角度进行黄土三轴数值试验敏感性分析。因此，根据室内三轴试验的结果获取的宏观参数，选择黄土特性细观参数的范围。运用三维颗粒流PFC3D软件进行常规三轴模拟试验，通过调节各细观参数值的范围，找到黄土细观参数与宏观力学性能之间关系，进一步研究各细观参数值变化对黄土宏观力学参数影响的敏感性，对建立黄土力学模型具有深远意义。

1 黄土三轴细观参数的标定

(1)

L=2R=R[A]+R[B]

(2)

1.1 点连接模型参数

在点连接接触模型中，仅仅能传递接触点所产生的接触力，不产生弯矩，此球体间的联系主要通过弹性梁承受力的宏观力学响应建立，从而完成宏观连接，所以可用法向强度和切向强度定义。设定此时弹性梁的横断面面积为A，惯性矩I，某个颗粒在任意方向的运动总时间为t，如式(3)和式(4)所示：

(3)

(4)

对于仅存在纯轴力和纯剪力的弹性梁，此时的弹性梁不能建立法向力学和切向力学的关系，弹性梁两端的接触刚度可表示为式(5)和式(6)：

(5)

(6)

当两个颗粒的大小相同时，则结合式(5)～式(6)，可以得到：

(7)

如式(7)所示，此公式中没有表示颗粒的泊松比，由此推断离散元颗粒的泊松比与刚度之间没有明确的联系，而实际土颗粒体系中其泊松比与土颗粒刚度比有关。颗粒刚度比能明显影响接触颗粒的法向力与切向力之比，从而影响离散元颗粒流体系的宏观破坏机理(张锐， 2005)。由上述分析，确定细观参数的方法可以为：通过实验先确定颗粒间的接触模量EC，其次设定刚度比，设定kn/ks，根据式(7)确定kn，最后结合刚度比公式计算ks。

对于仅存在纯轴向荷载T或纯剪切荷载V的弹性梁，则弹性梁横断面上的法向应力σ和切向应力τ可以表示为式(8)和式(9)：

(8)

(9)

对于弹性梁破坏的情况，可以用应力表示接触黏结模型参数的法向强度和切向强度，既将式(3)分别代入式(8)和式(9)得到式(10)和式(11)：

(10)

(11)

1.2 点平行连接模型参数

点平行连接模型是一系列弹簧组成的弹簧体，将弹簧接触点视为中心，且接触点弹簧平行并均匀地分布在接触平面上。可以把平行连接的弹簧视为长度L接近于零的弹性梁，当外力作用下弹簧体之间发生相对运动时，点平行连接会产生轴向力T、切向力V、弯矩M以及扭矩Mt等，可由式(12)和式(13)计算弹簧体之间的平行连接承受的最大法向力和最大切向力：

(12)

(13)

(14)

(15)

(16)

(17)

对于点平行连接仅存在纯轴向力和纯剪力的情况，无法将模型中的法向力学行为和切向力学行为建立联系。平行连接的法向刚度和切向接触刚度可以表示为式(18)和式(19)：

(18)

(19)

将式(15)带入式(19)得到：

(20)

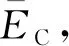
在某种程度上离散元模型中颗粒的法向刚度、刚度比、摩擦系数等细观对模拟试验结果都有很大影响，合理调整这些参数可以有效控制模拟试验结果。

2 黄土三轴试验的颗粒流数值模拟

2.1 室内三轴试验

本试验所用仪器为SLB-6A型应力-应变控制式三轴剪切渗透试验仪，其围压范围为0～1MPa，黏质土每分钟应变为0.05%～0.1%。试验用土取自陕西延安安塞地区，为褐黄色粉质黏土，三轴试验试样高80mm，直径39.1mm，控制试样分别在不同围压50kPa、100kPa、150kPa、200kPa， 剪切速率0.4mm·min-1条件下进行CU试验，其物理性质指标如表1所示，土料的颗粒分析曲线见图1。

表1 试验土样的基本力学参数

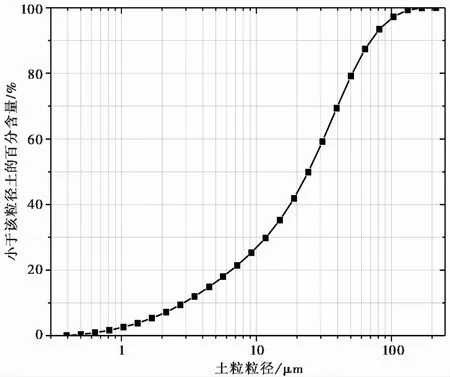
图1 黄土的颗粒级配曲线

2.2 颗粒流数值模拟

2.2.1 模型的建立

试验数值模拟分析采用线性接触模型，模型的建立分成2个步骤： ①设置符合实际的圆筒模型来约束散体结构，初始尺寸高为0.08m，直径为0.0391m； ②建立试验颗粒体试样，构成黄土结构体系的是骨架颗粒，实际试样颗粒成千上万，计算模型困难，为减小计算量，采用半径放大法，因此将颗粒粒径设置为6e-4～17e-4，并呈均匀分布。颗粒之间的黏结关系采用接触黏结方式，三轴计算模型如图2所示，颗粒体高度为80mm，直径为39.1mm，圆通模型高度112mm，上下各超出试样16mm。

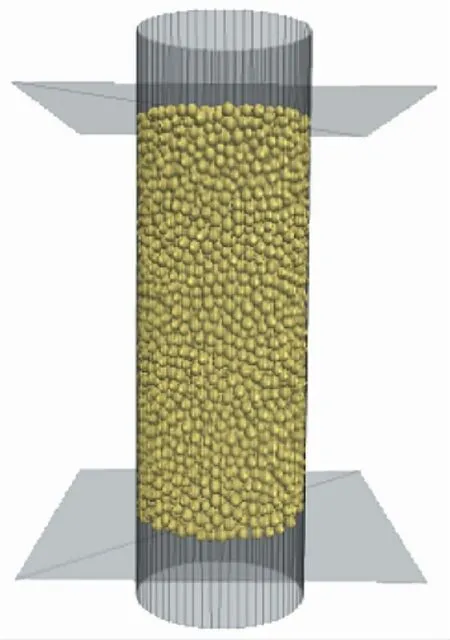
图2 颗粒流模型图

2.2.2 三轴数值模型基本参数的选取

根据室内三轴试验结果，得到试样在不同围压50kPa、100kPa、150kPa、200kPa下的偏应力最大值分别为142.8kPa、207.9kPa、290.0kPa、353.2kPa。根据式(21)和式(22)计算莫尔圆的圆心横坐标及莫尔圆的半径，摩尔应力圆如图3所示。由抗剪强度公式及图3中的莫尔圆拟合切线公式可得黏聚力c=24.09kPa，tanφ=0.45，摩擦角φ=24°。

图3 三轴试验的莫尔圆及强度包线

(21)

(22)

根据室内常规土工试验得到重塑黄土的单轴抗压强度UCS，代入公式

EC=429.56(UCS)0.9122

(23)

计算土体的接触模量为EC=3.64×104kPa，带入式(7)求解得kn=ks=0.8736×105kPa，本次模型设定kn=ks=1.0×105kPa，摩擦系数为0.45。模拟试样中颗粒粒径范围按照实测颗粒级配适当选取，最小颗粒粒径为0.6×10-3m，最大颗粒径为1.7×10-3m。此模型试验颗粒基本计算参数如表2所示。图4中虚线代表三轴试验数值模拟值，实线代表室内三轴试验值，由图可知，数值模拟值与室内试验值都会随着围压的增大而增大，当围压为50kPa时，应力-应变曲线趋势基本一致，但是，随着围压的逐渐增大，数值模拟试验应力-应变曲线呈软化性发展，而室内试验结果与之相反，这与 Potyondy et al.(2004)的分析是一致的，主要原因在于 PFC 的基本单元为刚性圆球，颗粒形状及排列形式单一、颗粒之间相互嵌固及咬合作用力弱，虽然引进了接触黏结来提高颗粒间接触力，但随着轴向荷载的增大，黏结破裂，其对抗剪强度的贡献极为有限，与实际粗粒土强度特性相差较大。

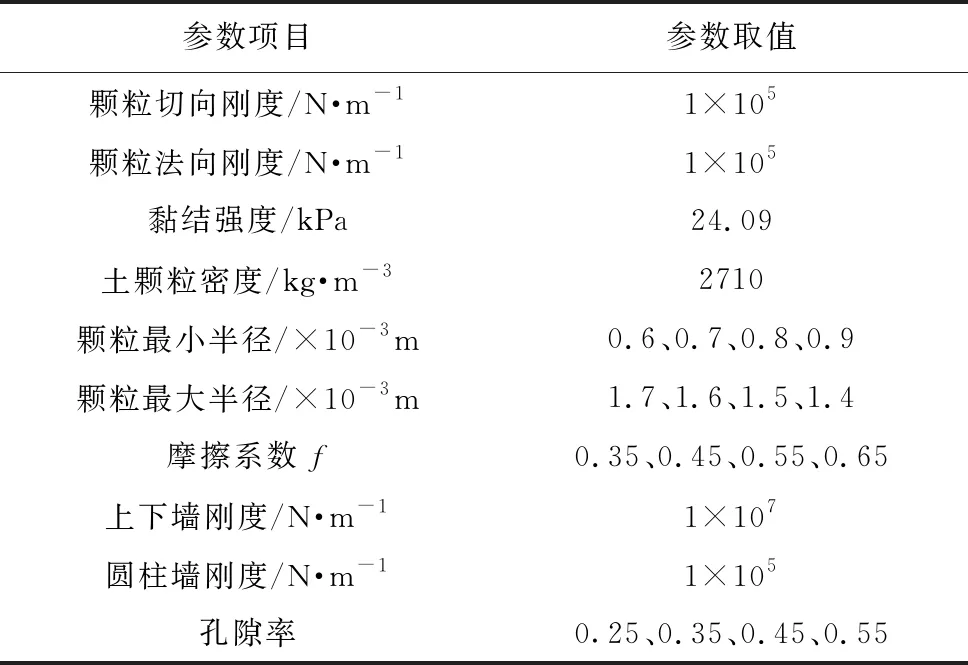
表2 颗粒基本计算参数

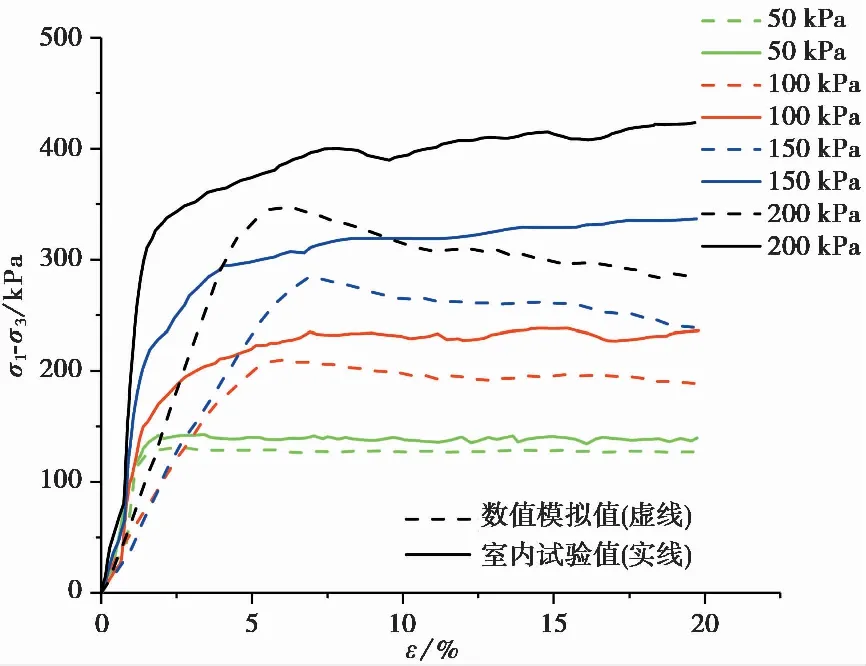
图4 三轴试验数值模拟值与试验值对比

3 黄土三轴细观参数敏感性分析

影响三轴数值试样抗剪强度及变形的因素很多，土体抗剪强度与其影响因素的关系式如式(24)所示(谢定义等， 2008)：

(24)

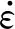
故以室内试验所得值为基本计算参数，再结合离散元理论中固有的参数，通过调节各细观参数值的范围研究其对黄土应力-应变特性的敏感性，为今后三轴试验PFC3D模拟参数的调整作一些参考，本文细观参数选取摩擦系数、孔隙率、颗粒法向刚度与切向刚度比(kn/ks)、颗粒粒径分布。

3.1 摩擦系数

以摩擦系数为变量，室内试验所得基本参数为不变量，在围压为50kPa、100kPa、150kPa、200kPa的条件下分别设置摩擦系数值为0.35， 0.45， 0.55， 0.65，研究细观参数摩擦系数对黄土宏观力学特性及变形的影响。摩擦系数对黄土应力-应变曲线的影响如图5所示，对峰值强度和剩余强度影响曲线如图6和图7所示。由图6所示，不同围压下黄土数值试样的峰值强度均会随着摩擦系数的增加呈不断增大的趋势，且增大趋势不明显，表现出正相关性。此现象可以理解为：由于黄土颗粒间摩擦系数的增大，会提升土体的摩擦强度(包括颗粒的滑动摩擦和咬合摩擦)，从而增加了颗粒接触处的摩擦力和颗粒间的咬合作用，使得颗粒发生错动、转动和滑动时所需要的应力会更大，因而也就提高了试样的峰值强度。

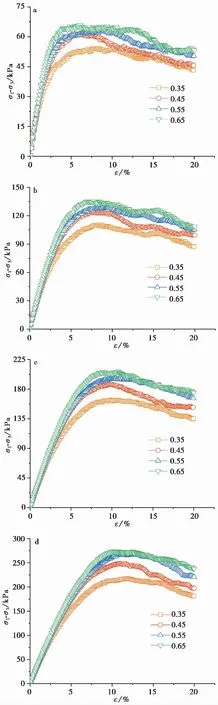
图5 不同围压下摩擦系数对应力-应变曲线的影响

图6 不同围压下摩擦系数对峰值强度的影响

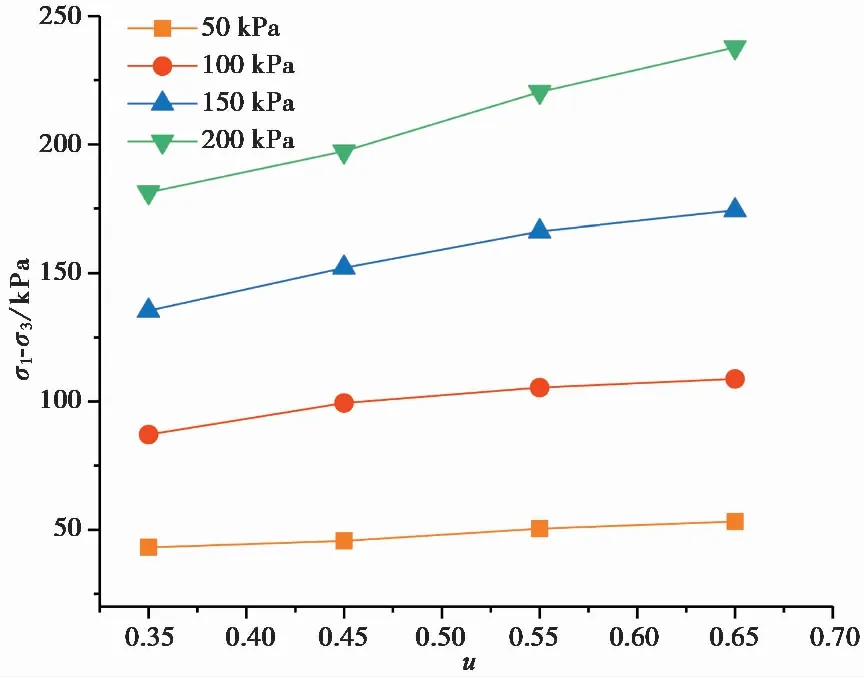
图7 不同围压下摩擦系数对剩余强度的影响

由图5应力-应变曲线可以看出颗粒间摩擦系数的增加可使土样应变软化特性加剧，并且黄土试样材料初始的线弹性模量基本上不受其颗粒间的摩擦系数的影响，这是由于土样的黏结强度充分发挥作用时应变不同步造成的，在试样加载初期，黏结强度首先发挥作用，应变较小时，黏结强度就可以达到极限值，随着应变的增加，颗粒间的黏结发生破坏，之后试样中只有剪胀力和颗粒间的摩擦强度起作用。当应变达到一定值时，试样体积不再发生变化，试样中仅剩摩擦力起作用，所以对于接触黏结相同的试样，加载初期试样初始弹性模量一般不发生变化。

图6表示不同围压下峰值强度与摩擦系数的关系，高围压下的峰值强度要远大于低围压下的峰值强度，当围压较低时(50kPa、100kPa)，细观参数摩擦系数对峰值强度的影响不明显，高围压下，峰值强度随着摩擦系数有逐渐增大的趋势。初步判断原因为：数值试样在加载过程中，当颗粒的转动或剪切力过大造成黏结破坏时，作用于颗粒接触处的残余力主要取决于周围压力及颗粒间的摩擦系数(耿丽等， 2011)。在围压较小时，试样内部结构较为松散，颗粒间接触面积较小，使颗粒间接触摩擦力不能完全发挥作用。围压的逐渐增大致使颗粒间接触更为紧密，接触处产生更大的摩擦力抑制颗粒间的转动或滑移，此时颗粒间相互作用也逐渐增大，所以试样的抗剪强度增大。

如图7表示不同围压下剩余强度与摩擦系数的关系，剩余强度则在摩擦系数较小时(0.35、0.45)增加缓慢，当达到0.55时，摩擦系数对剩余强度的影响变小。三维离散元中，当试样中形成剪切带后，颗粒之间会产生挤压与错动，但并不会分开，如果在试样周围施加压力时，模型中颗粒间的接触力不仅有摩擦力，还有侧向接触力以及竖向接触力，这时三维试样模型中摩擦系数不是影响剩余强度的唯一因素。

以本次试验所得基本摩擦系数0.45为参照，低围压下(50kPa、100kPa)，当摩擦系数从0.45增大到0.55时，峰值抗剪强度分别从61.99kPa增加到63.25kPa， 123.94kPa增加到128.73kPa，增加幅度在2%～4%之间，剩余强度从45.66kPa增加到50.48kPa， 99.38kPa增加到105.39kPa，增加幅度在5.7%～9.5%之间。当围压较高时(200kPa)，峰值抗剪强度从197.29kPa增加到220.44kPa，增加幅度为10.5%，剩余强度从220.44kPa增加到237.85kPa，增加幅度为7.3%。所以不同围压下细观参数摩擦系数对黄土峰值抗剪强度及剩余强度的影响都较小。

3.2 孔隙率

土的孔隙率是指土中孔隙的体积VV和土的总体积V之比，如式(25)所示，其中，VV表示土样中孔隙的体积，V表示土样的总体积。

(25)

孔隙率是影响黄土抗剪强度及变形的重要因素之一。本文根据室内三轴试验，在围压50kPa、100kPa、150kPa、200kPa的条件下，分别设定孔隙率为0.25、0.35、0.45以及0.55下的三轴数值模拟试验，在不同围压下应力-应变曲线如图8所示。结果表明，保持其他细观参数不变，调节孔隙率在指定范围内增加，黄土数值模拟试样的峰值强度均呈现明显的减小趋势，且达到峰值强度时所对应的轴应变在逐渐增大。黄土的应力-应变曲线逐渐也由孔隙率较低时的应变软化型向孔隙率较高时的应变硬化型发展。孔隙率较小时，剪切破坏时试样出现脆性破坏，当孔隙率为0.45时，试样表现出明显的体缩效应(刘勇等， 2014)。在不同围压下，峰值强度与孔隙率的拟合曲线如图9所示，呈一次函数关系。

图8 孔隙率对应力-应变曲线的影响

图9 孔隙率与模型试样峰值强度的拟合曲线

因此，模型试样孔隙率在一定范围内变化将显著影响黄土峰值剪切强度以及剩余强度，以模拟实验基本细观参数孔隙率0.45为参照，由于在不同围压下孔隙率对峰值抗剪强度的影响规律相近，选择200kPa围压进行分析，当孔隙率从0.35增加到0.45时，峰值抗剪强度从347.83kPa减小到249.01kPa，减小幅度为28.4%。剩余强度从243.28kPa减小到197.29kPa，减小幅度为18.9%，对材料峰值强度的影响较剩余强度大。

3.3 颗粒法向刚度与切向刚度的比值(kn/ks)

kn/ks是颗粒法向刚度与切向刚度之比。以室内试验所得基本参数为不变量，改变颗粒的竖向接触刚度与切向接触刚度之比kn/ks分别为1、5、10、20，得到在围压50kPa、100kPa、150kPa、200kPa下的应力-应变曲线如图10所示。保持颗粒法向刚度不变，增加颗粒刚度比，应力-应变曲线中的初始切线模量的变化较小，这说明颗粒切向刚度的变化对黄土材料的初始的线弹性模量影响不大。低围压下(50kPa、100kPa)，随着颗粒刚度比的增加，数值试样的峰值强度均会出现减弱的趋势，减小幅度较明显。高围压下(200kPa)，数值试样的峰值强度出现减弱的趋势，减弱趋势不明显。不断减小切向刚度，降低试样的切向抗变形能力，并且不断增大刚度比kn/ks的值，会使模型试样的破坏形式由形成剪切面破坏转变为以侧向应变增加形成的破坏为主，数值试样中颗粒刚度比的改变会导致试样的峰值强度及剩余强度也产生一些差异性。应力-应变曲线在峰值强度之后均表现出下降趋势，具有一定的应变软化特性，且高围压下的应变软化现象更明显。

图10 不同围压下刚度比对黄土应力-应变曲线的影响

在低围压下(50kPa)，当刚度比kn/ks的值从1增加到5时，数值试样峰值抗剪强度的值由73.23kPa减小到69.18kPa，减小幅度5.5%，剩余强度的值从59.78kPa减小到53.53kPa，减小幅度为10.5%。高围压下(200kPa)，数值试样峰值强度的值从309.29kPa减小到296.64kPa，减小幅度4.1%，剩余强度的值从257.65kPa减小到252.00kPa，减小幅度为2.2%。所以低围压下刚度比的增加对数值试样峰值抗剪强度和剩余强度的影响比高围压下的大。

3.4 颗粒粒径分布

以室内实验所得基本参数为不变量，改变颗粒粒径的分布范围分别为0.6e-3～1.7e-3、0.7e-3～1.6e-3、0.8e-3～1.5e-3、0.9e-3～1.4e-3之间，分别在50kPa、100kPa、150kPa、200kPa围压下进行三轴模拟剪切试验。不同最小颗粒粒径条件下应力-应变曲线如图11。

对粗粒土进行了不同颗粒粒径下的常规三轴模拟实验，发现当颗粒粒径在0.1～1mm之间波动时，试样颗粒粒径对试样峰值强度影响较小(张志华， 2015)。本次模拟结果如图11所示，不同围压下，随着最小颗粒粒径的增大，对模型试样的峰值抗剪强度和剩余强度的影响相当小，且均出现应变软化现象。初步判断原因是：当围压一定时，试样的峰值应力随着最小颗粒粒径的减小逐渐下移，应变硬化程度减弱。由于最小颗粒粒径越小，其模型试样级配分布越好，生成的模型试验中大颗粒形成架空骨架体系，在一定外力作用下，较小直径颗粒落入大骨架体系，颗粒排列更加紧密，会产生较大的接触力，从而利于摩擦力的生成，试样强度提高。

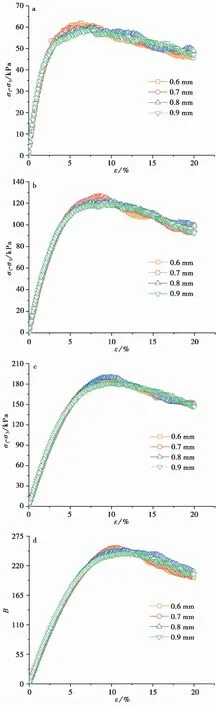
图11 不同围压下最小颗粒粒径对黄土应力-应变曲线的影响

如图12所示，当试样最小颗粒粒径为较小时(0.6mm， 0.7mm)时，模型试样在剪切结束后颗粒移动位移场分布较为明显，上部颗粒主要向左下方移动，下部颗粒主要向右下方移动，模型试样颗粒位移场被分为两个部分。当试样最小颗粒粒径较大时(0.8mm， 0.9mm)，模型试样颗粒在剪切结束后移动方向没有规律性，当最小颗粒粒径为0.9mm时最为明显，模型试样中的颗粒粒径相差不大，多数颗粒向下运动，试样分块现象不明显。

图12 不同最小颗粒粒径下的颗粒位移场(200kPa)

不同围压下孔隙率对峰值抗剪强度的影响规律相近，选择200kPa围压下的颗粒粒径分布应力-应变曲线进行分析，当最小半径从0.6mm增加到0.7mm时，峰值强度从249.01kPa减小到253.78kPa，减小幅度为1.9%，剩余强度从201.82kPa减小到199.23kPa，减小幅度为1.3%，所以颗粒粒径分布对试样的峰值抗剪强度及剩余强度影响相当小。

3.5 多因素正交试验设计

对摩擦系数、孔隙比、颗粒刚度比、颗粒最小粒径等多种影响因素的4个水平进行正交试验设计，从而对抗剪强度的影响程度进行敏感性分析。假设显著性水平为0.05，4种因素的4种影响水平如表3所示，在200kPa围压下分别进行如表4中16组正交试验，正交试验结果如表5所示：

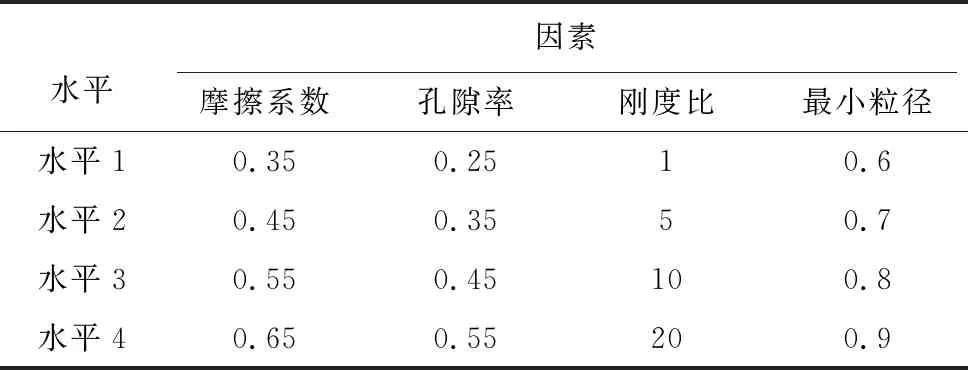
表3 4种因素的4种影响水平

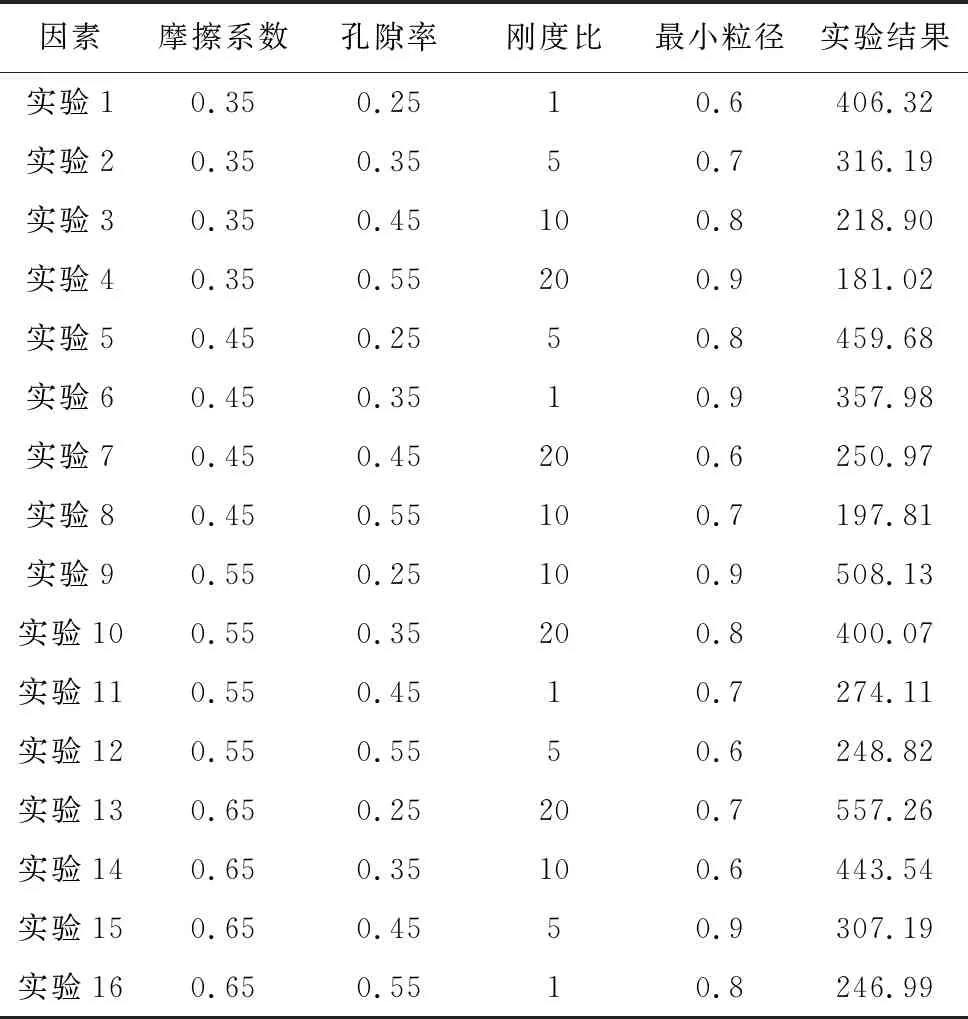
表4 正交试验设计

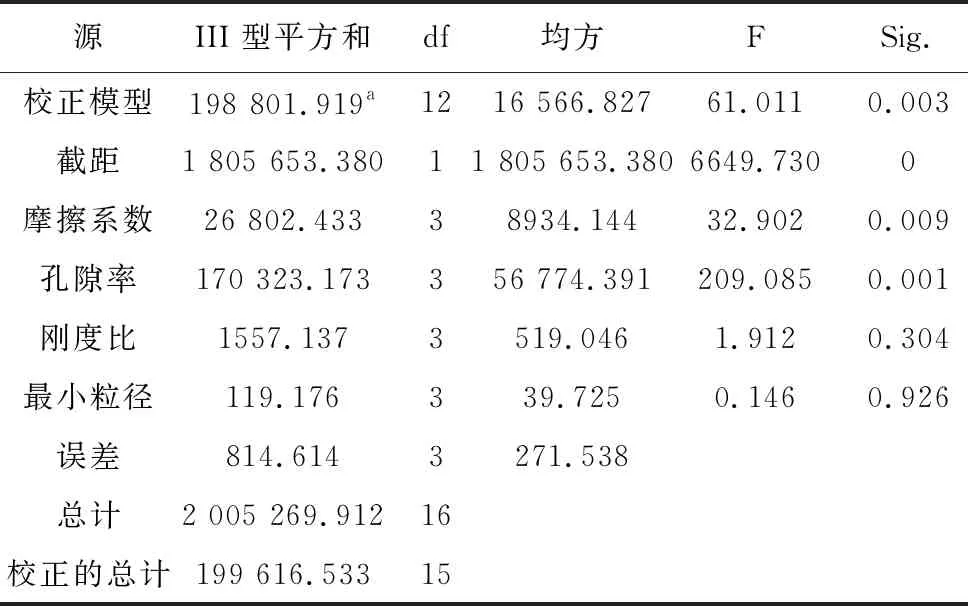
表5 正交试验结果

用IBM SPSS Statistics分析正交试验结果如表5所示，因变量为每组试验的最大偏应力，则摩擦系数和孔隙率对试验结果影响显著，颗粒最小粒径和刚度比对实验结果影响不大，影响程度大小排序为：孔隙率>颗粒间摩擦系数>颗粒刚度比>颗粒最小粒径，此实验结果与文章中量化数值分析结果一致。

4 结 论

(1)围压较低时(50kPa、100kPa)，摩擦系数对试样峰值强度及剩余强度的影响都较小，围压越大，影响越大，且影响程度均不超过11%。

(2)随着孔隙率在一定范围内变化，不同围压下模型试样孔隙率与峰值强度的拟合曲线均呈一次函数关系，随着孔隙率的减小，模型试样的应力-应变曲线应变软化现象加剧，并且孔隙率对试样峰值强度的影响比剩余强度大。

(3)当围压不变时，数值试样的峰值强度和剩余强度均会随着颗粒刚度比的增大而减小，并且低围压下刚度比对数值试样峰值抗剪强度和剩余强度的影响比高围压下的显著。

(4)数值试样最小颗粒粒径的变化对数值试样的峰值抗剪强度和剩余强度的影响相当小，平均影响程度小于2%。模型试样在剪切结束后，最小颗粒粒径较小时(0.6mm， 0.7mm)的颗粒移动位移场分布比最小颗粒粒径较大时(0.9mm)明显。

(5)不同围压下，对试样峰值强度及剩余强度影响最大的细观参数为孔隙率，影响最小的为颗粒粒径分布，且低围压下(50kPa)颗粒刚度比对两者的影响比高围压下(200kPa)的大。对数值试样初始线弹性模量与应变软化特性影响最大的细观参数为孔隙率，颗粒刚度比次之，颗粒粒径分布最小。200kPa围压下的正交试验验证结果与数值分析结果一致。