高中数学解题中数形结合思想的有效应用
2021-11-24宁邦青
宁邦青
(广西钦州市浦北县浦北中学 535300)
“数”与“形”有着紧密的联系,在解题中通过“数”与“形”的转化,能够及时的找到解题的切入点,因此,实践中既要注重数形结合思想理论的渗透,又要做好该思想在解题中的应用示范,使学生牢固掌握,灵活应用该思想解题.
一、用于解答函数零点个数问题
函数零点问题是高中数学中的一类重要问题.解答该类问题应具体情况具体分析,结合零点的几何定义,巧妙的运用数形结合思想化难为易,尤其在求解函数零点个数时应用数形结合思想,可达到事半功倍的良好效果.解答该类习题的关键在于正确的画出函数图象,因此,实践中应引导学生夯实基础,熟练掌握函数的奇偶性、单调性、周期性等,并能熟练的加以推导.
例1已知定义在R上的偶函数y=f(x)满足f(2-x)=f(x).当0≤x≤1时,f(x)=x,设函数g(x)=f(x)-log5|x|,则g(x)的零点个数为( ).
A.6 B.7 C.8 D.9
由函数零点的定义可将该题转化为函数y=f(x)和函数y=log5|x|图象交点个数问题.先研究两个函数在x>0上的图象,而后结合图象的对称性,找到在R上的总的交点个数.
因为f(2-x)=f(x),所以其图象关于x=1对称.又因其为偶函数,则满足f(x)=f(-x),得到其周期T=2,由此不难画出x>0的函数图象.由y=log5|x|可知其为偶函数.当x>0时,函数y=f(x)和函数y=log5x的图象如图1所示,此时的交点个数为4个.当x<0时,由对称性可知交点个数也为4个,总的交点个数为8个,选择C项.

图1
二、用于解答三角函数问题
三角函数在高中数学中占有重要地位.相关习题灵活多变,解题思路多种多样,其中三角函数的最值、周期等,能够从其图象中获得,因此,解题中应注重运用数形结合思想,通过画出对应的图象,直观的揭示相关参数之间的关系,并注重联系三角函数的性质,以快速解答相关习题.
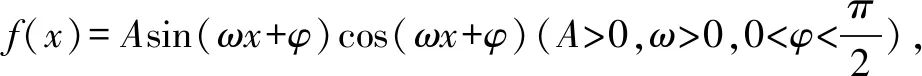
A.在区间[-4,2]上单调递增
B.在区间[0,6]上单调递减
C.在区间[1,7]上单调递减
D.在区间[4,10]上单调递增
审题可知,该题需要根据已知条件求出参数A、ω、φ的值,得出函数g(x)的具体表达式,而后运用三角函数性质,判断其在特定区间上的单调性.
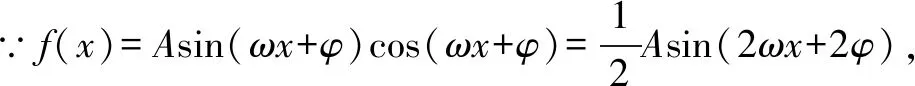
三、用于解答平面向量问题
平面向量是高中数学的重要基础知识.在相关测试以及高考中该部分知识既可以单独考查,也可以与其他知识结合起来考查.解答平面向量问题的常规思路有两种:运用向量的几何运算;运用向量的坐标运算;在两种解题思路中数形结合思想发挥着关键作用.结合平面向量问题的解答,让学生体会数形结合思想的便捷性,培养学生数形结合思想应用意识,结合经典例题解答,提高学生解题能力.
例3已知平面向量a、b、c,满足a+b+c=0,其中a、b的夹角为α,|a|=1,|b|+|c|=2,则cosα的取值范围为____.
解答该题如采用常规作答较为繁琐,难度较大,而使用数形结合思想可很快的得出正确答案.解题的关键在于如何理解与应用题干中“|b|+|c|=2”这一条件.事实上,由|b|+|c|=2可联想到椭圆定义,将其放到椭圆中分析.
根据题意画出图形,如图3所示,其中F1和F2为椭圆的左右焦点,向量a、b、c随着点P运动,向量a以及向量a、b的夹角不断变化,显然α∈[0,180°],则cosα的取值范围为[-1,1].

图3
四、用于解答直线方程问题
直线方程属于高中数学中解析几何范畴.解析几何给学生留下的印象是计算繁琐,难度较大.事实上学习时不能一概而论,应具体问题具体分析灵活采用多种解题思路,以达到迅速求解出正确结果的目的.数形结合思想用于解答相关习题,可避免繁琐的计算,运用几何知识经过简单的分析与运算,便能得出正确结果.
例4在平面直角坐标系中,动点P(a,b)满足|a|+|b|=1,设d为点P到直线x-my-2=0的距离,当a、b、m变化时,d的最大值为( ).
A.1 B.2 C.3 D.4
解答该题如采用常规方法一时难以切入,而且即便能够切入,但计算较为繁琐,不易得出正确答案.事实上只要思路正确,该题不难解答.解答该题的关键在于能够看懂点P轨迹表示的图形,借助数形结合思想进行分析判断.在画“|a|+|b|=1”表示的图形时,可采用分类讨论法将绝对值去掉.

图4
数形结合思想在高中数学解题中有着广泛的应用.实践中应充分认识到这一思想的重要性,结合教学内容做好数形结合思想理论知识的讲解,使学生掌握“数”与“形”联系的常规思路,能够熟练的画出高中数学常见的函数图象、图形.同时,做好经典例题的讲解,使学生把握运用数形结合思想解题的相关细节,不断的提高其运用数形结合思想解题的灵活性与正确性.
