基于双DDPG的全局自适应滤波器剪枝方法

王彩玲，王 炯，蒋国平

（南京邮电大学自动化学院、人工智能学院，江苏南京 210023）

卷积神经网络凭借着卓越的性能表现在图像分类［1］、目标检测［2－3］、语义分割［4］等计算机视觉任务中得到了广泛的应用。然而这些具有卓越性能的深度神经网络模型往往需要更高的算力开销和更大的内存空间，因此很难部署在算力和内存资源受限的移动和穿戴设备上，这极大地限制了其实际应用。为了将深度神经网络应用于实际，研究人员开始把更多的目光聚集于深度网络模型压缩方法的研究。最近被证实这些深度神经网络通常都是过参数化的［5］。在删除那些过渡参数化模型中的部分权值、激励或者层的情况下，并不会引起网络模型性能的显著下降［6］。这使得在保证网络性能良好的前提下，对网络模型进行压缩成为可能。目前，众多压缩深度神经网络模型的方法被研究人员相继提出。常用的 方法 有 网络 剪 枝［7－9］、 低 秩分解［10］、 知识 蒸馏［11］、高效的神经架构［12］和参数量化［13］。

剪枝，作为压缩深度神经网络模型的主流方法之一，可以极大地减小内存占用和推理运算时间。在过去的十年内，激起了广大研究者的兴趣。剪枝主要分为结构化剪枝和非结构化剪枝。非结构化剪枝是将不重要的权值设置为0，从而实现高稀疏性，但是稀疏操作需要专门的硬件或者软件库来加快推理过程，因此限制了非结构化剪枝的应用。结构化剪枝则是移除原始网络中不重要的滤波器（通道）。这种滤波器（通道）级别的剪枝只是对网络模型的架构进行修改，并不会影响它的实际可用性。本文致力于通过滤波器剪枝来减少模型参数和加速模型运算，为低内存和低计算力的设备提供一个通用的策略。

滤波器剪枝的核心是根据设计好的评价标准，在保证网络的性能不出现显著下降的情况下，选择并移除网络模型中评价出的不重要滤波器。本文采用的是滤波器权值的信息熵作为该滤波器的重要性评价标准。滤波器的信息熵越大，则该滤波器对整个网络而言越重要。

为了获得具有紧凑性的模型，大多数方法是根据研究者的经验对网络模型的每一层使用固定的压缩率进行剪枝［6，9］。 然而，这种根据经验设置剪枝率的策略无法得到网络模型的最优结构。LEGR［14］算法率先引入了全局剪枝的概念，通过遗传进化算法将滤波器在当前层中的局部重要性转化成在整个网络模型中的全局重要性。但是该算法充满了不确定性，学习出的结果并不一定是最优的。为此本文提出基于双DDPG算法学习全局重要性的概念，即利用两个DDPG分别学习出该卷积层中的每一个滤波器在整个网络中的全局规模系数和全局偏差系数，从而实现全局重要性转换。

最近，对剪枝得到的网络从头开始训练的效果比微调的效果好［15］已被证实。为了进一步提高剪枝后网络的表达能力，本文采用基于网络参数自适应加权的多个相同网络联合并行训练。

1 相关研究

作为模型压缩的主流方法之一，剪枝在一定程度上可以压缩模型或者加速模型推理运算。网络剪枝的主要思想是在不损失太多性能的情况下，减少原始网络中冗余的权值和连接，得到一个紧凑的网络。剪枝一般可分为两大类：权重剪枝和滤波器剪枝（也称通道剪枝）。

权重剪枝是Lecun等［8］在1990年首次提出的消除神经网络中不重要的权值参数的概念，并且提出了根据网络参数的二阶偏导值作为评价参数重要性的方法。 Li等［6］提出了一种基于l⁃1范数重要性准则的剪枝方法，然后对剪枝后的网络进行微调以恢复性能。Guo等［7］引入了动态剪枝的概念，利用动态剪枝来降低网络的复杂度，将剪枝融入到训练过程中，从而避免了错误剪枝。Aghasi等［16］则是设计了一个求解凸优化的程序，在每一层寻找一个稀疏的权值集，删除层中不重要的连接，同时保持了层的输入和输出与最初训练的模型一致。Liu等［17］根据卷积层中空间的相关性提出了一种频域动态剪枝的方案。在每次迭代中对频域系数进行动态剪枝，并根据不同频带对精度的重要性，对不同频带进行区分剪枝。

权重剪枝是非结构化的剪枝，往往会产生稀疏权值矩阵，如果没有专门的软件库或者硬件进行辅助处理是无法直接提高推理效率和减少内存空间占用。

滤波器（通道）剪枝是一种结构化的剪枝，在滤波器（通道）或者层的级别上删除冗余的权值。通道剪枝能减少网络模型占用的存储空间和降低其在线推理的计算量。 Li等［6］提出了基于l⁃1范数的判断准则，通过这种准则识别出对输出精度较小影响的滤波器，从而移除该滤波器及其连接的特征图，减少了计算开销。He等［18］采用的是从零开始训练和同时修剪模型的软滤波器剪枝策略，可以有更大的容量用于训练数据的学习。Huang等［19］把剪枝作为一个优化问题，引入了一种新的参数缩放因子来缩放特定结构的输出，然后把稀疏正则化加入到这些因子上，用随机加速近端梯度（APG）方法求解该优化问题。通过将一部分因子置为0，则可以移除相应的结构。Luo等［20］提出了一个高效统一的ThiNet框架，从下一层中提取相关信息去评判当前层中每一个滤波器的重要性。训练阶段和推理阶段均在加速和压缩CNN模型。Lin等［9］利用低秩的特征映射包含更少的信息和剪枝后的结果可以很容易地复制的特点，提出了一种基于高秩特征映射（HRank）的滤波器剪枝方法。从网络架构角度出发，结构剪枝的目的就是架构最优的子网络。但是这些方法均是预先定义好的体系架构，即根据经验提前设置好每一层的剪枝率。这样得到的模型架构并不是最优的模型架构，存在一定偏差。He等［21］率先提出了基于强化学习的AutoML压缩策略对模型进行压缩。Lin等［22］把寻找最优的剪枝结构作为目标，提出一种基于人工蜂群算法（ABC）的通道剪枝方法。Chin等［14］提出一种学习全局重要性剪枝的概念，即把滤波器在卷积层中的局部重要性经过遗传进化算法（EA算法）转换成全局重要性，从网络整体角度对每一层中的滤波器进行剪枝。

在训练过程中由于参数的减少，网络模型通常收敛于局部最优解。Liu等［15］表明，从零开始训练修剪后的模型也可以取得与微调相当甚至更好的性能。

虽然这些方法取得了一定的效果，但仍存在剪枝过程耗时较长、未充分移除模型中的冗余参数以及未完全恢复剪枝后模型的性能等不足之处。针对上述问题，提出了一种基于双DDPG的全局自适应滤波器剪枝方法。基于双深度确定性策略梯度（DDPG）算法，从全局角度对网络模型进行准确剪枝。在剪枝完成后进行多网络联合训练，充分恢复网络模型的性能。

2 本文方法

本文方法主要分为基于滤波器权值⁃信息熵的局部重要性、基于双DDPG学习全局重要性的剪枝和基于权值自适应加权的多个相同网络联合并行训练3个部分。前者是负责计算出每个滤波器在当前卷积层中的信息熵，并作为其局部重要性得分。中间的做法是利用双DDPG算法学习出深度网络模型中每一个卷积层的全局规模系数和全局偏差系数，结合局部重要性得分即可求出每一个滤波器的全局重要性得分。随后根据滤波器的全局重要性得分大小进行排序，并移除得分较小的滤波器。后者是一种新的训练方法，对剪枝后的模型进行复制。对复制得到的多个相同子网络采用不同的学习率和权值衰减同步并行训练。在训练过程中基于网络模型中每个卷积层权值的信息熵对多网络之间卷积层的权值自适应加权融合。

2.1 基于滤波器权值⁃信息熵的局部重要性

基于启发式方法评估权值重要性是目前常用的剪枝策略，如基于输出特征映射的秩作为权值的重要性判断标准［9］。

熵是许多启发式方法的起源。熵值越大，表明系统越混乱，网络模型能从输入图像中提取出的信息也就越多［23］。即对于网络模型中的滤波器（通道）而言，其权值的信息熵越小，在网络中其重要性就越低。与滤波器权值的大小相比，滤波器权值的信息熵更能代表当前滤波器的重要性［24］。

假设 Wi，j∈ RNi×K×K为第 i个卷积层中第 j个滤波器的权值，其中Ni表示该层的输入通道数，K×K表示滤波器中卷积核的大小。即当Wi，j的信息熵较小时，该滤波器从输入中提取出的信息量就越少，对网络模型的作用也就越小，可判定该滤波器为冗余的。假设Wi，j的元素值都是从随机变量X的分布中采样，并使用信息熵来度量该分布。为了进一步计算卷积层中滤波器的信息熵，把Wi，j中元素值的范围均匀地分成N个区间，然后计算出每个区间的概率。最后，可以计算出该滤波器的信息熵为

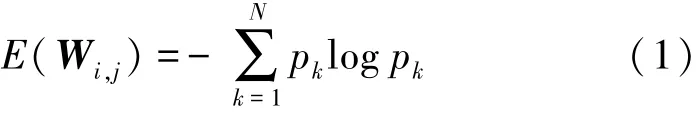
其中，pk表示第k个区间内的元素个数占总元素个数的比值。

假设i层有C个过滤器，那么第i层的总信息熵为

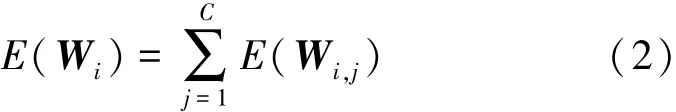
式（1）和式（2）均是从单个滤波器角度出发计算滤波器和卷积层的信息熵，却忽略了层中滤波器与滤波器之间的相关性。于是从层的角度计算信息熵，则网络模型第i层的信息熵为

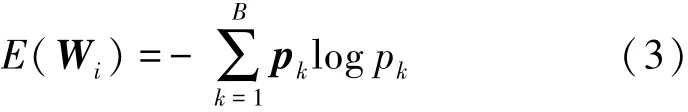
假设Ii，j为卷积神经网络模型第i层中第j个滤波器的局部重要性，即

2.2 基于双DDPG学习全局重要性的剪枝

结构化的滤波器剪枝方法通常可以表示为

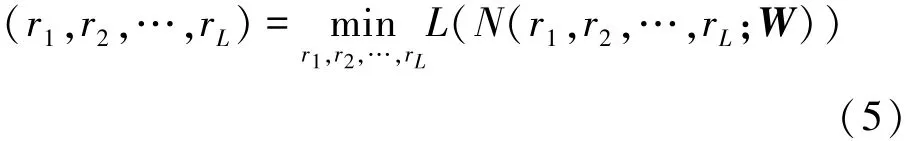
其中，L表示损失函数，N和W分别表示神经网络模型及其参数，ri表示第i层的剪枝率。假设ci表示模型N中第i个滤波器个数，c′i表示剪枝后模型N′中第i个滤波器个数，即

大多数剪枝方法都是根据经验，固定每一层的剪枝率ri。 LEGR［14］中率先提出了学习全局重要性剪枝的概念，即利用遗传进化算法计算出每一层对应的全局规模系数α和全局偏差系数κ。 其中 α ∈RL，κ ∈RL。 但是其采用的遗传进化算法迭代时间较久，且不能保证找到最优解。设αi和κi分别表示第i层的全局重要性规模系数和全局偏差系数。为了快速而又准确地计算出每一层的 αi和 κi，本文提出了一种基于双DDPG的学习全局重要性剪枝算法。算法流程如图1所示。

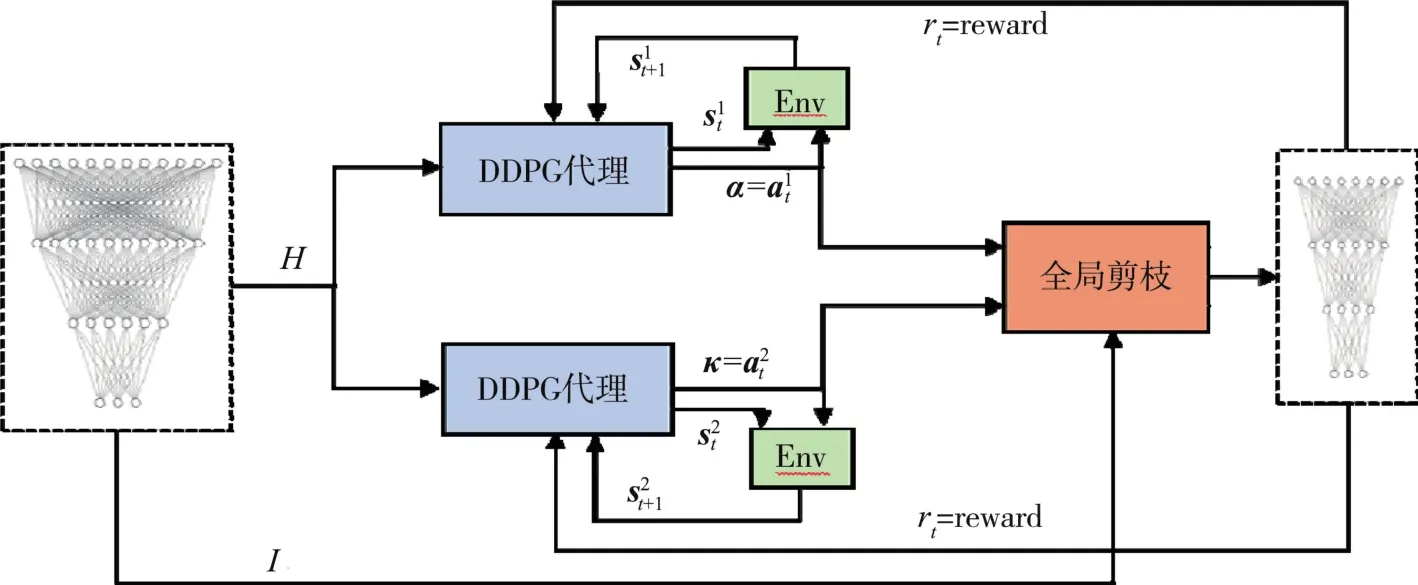
图1 基于双DDPG的学习全局重要性剪枝算法流程图

首先把网络模型N的每一层的信息熵集合H＝｛E（W1），…，E（WL）｝ 作为 DDPG1和 DDPG2的初始化输入s10和s20。 把DDPG1和DDPG2的第t次迭代的输出a1t和a2t作为网络模型N的全局规模系数α和全局偏差系数κ。 即

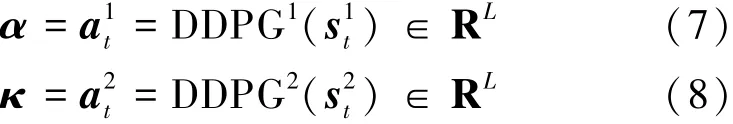
即对于每一层，根据其αi和κi，可以计算出每一层中滤波器的全局重要性即

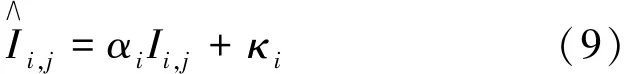
然后基于全局重要性进行排名，根据设置的剪枝率求出相应的阈值t，即

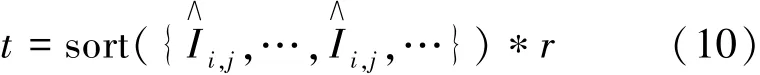
其中r表示对整个网络模型的目标剪枝率。由阈值t即可求出， 即

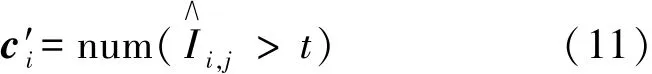
结合式（6）和（10）可以得到每一层的剪枝率 （r1，r2，…，rL）。 剪枝过程如图2所示。

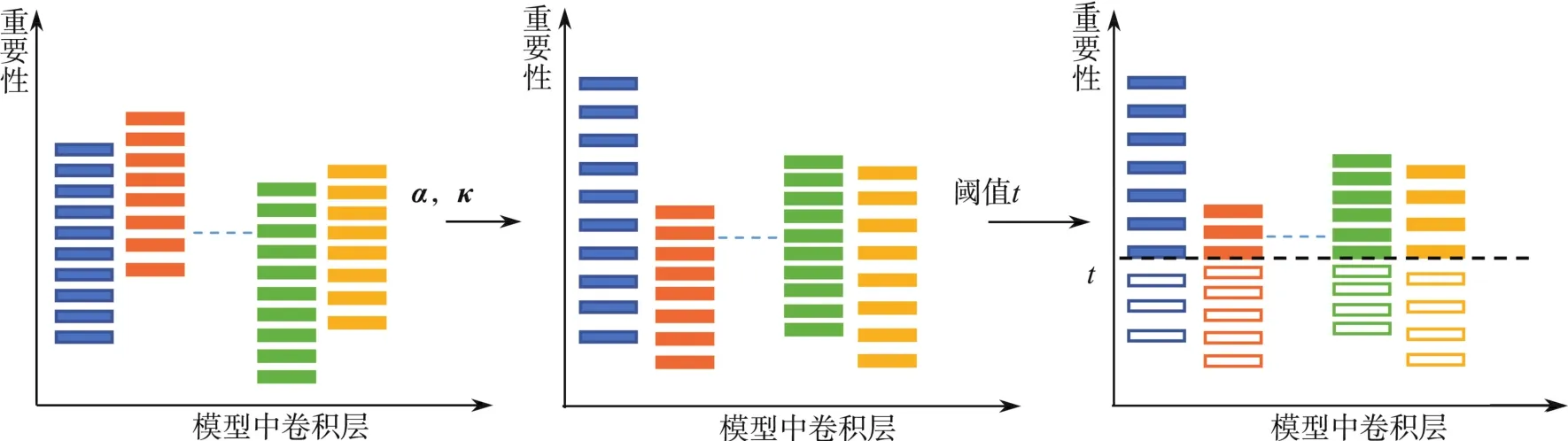
图2 全局剪枝过程

把剪枝后得到的子网络模型 N′的准确度Acc（N′）作为反馈约束 reward返回给 DDPG1和DDPG2。

DDPG：采用DDPG的目的是寻找出连续变动空间中的最优值（最优的α和κ）。 DDPG的结构如图3所示。

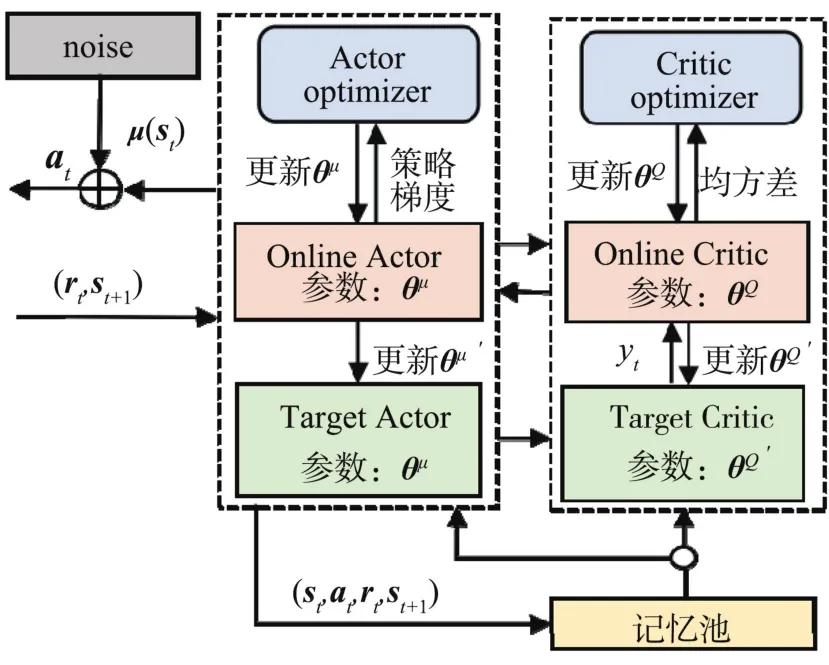
图3 DDPG代理结构

本文策略与 AGMC［25］和 AMC［21］相似，采用截断式正态分布进行噪声处理

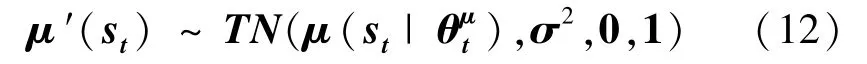
用损失函数更新DDPG代理

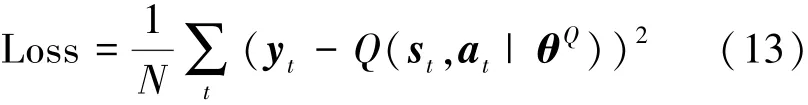
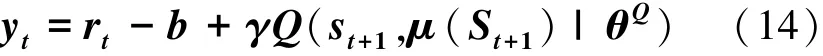
其中rt＝reward＝Acc（N′）为反馈约束。

Env：模拟环境，根据当前的st和at生成下一个状态的 st＋1， 即

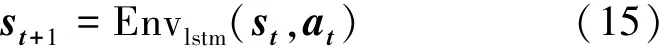
其更新策略采用的是相应DDPG代理中Actor optimizer的更新策略。

2.3 基于权值自适应加权的多个相同网络联合并行训练

剪枝后的模型由于网络参数的减少，在训练过程中极易陷入局部最优解。为此采用了嫁接［26］的策略，即对得到的最优子网络进行基于权值自适应加权的多个相同网络联合并行训练。

首先对剪枝得到的子网络进行复制，然后对复制得到的多个子网络采用不同的学习率和权重衰减率同时进行训练。当所有子网络使用训练样本完成一轮迭代之后进行一次网络之间权值自适应加权，过程如图4所示。

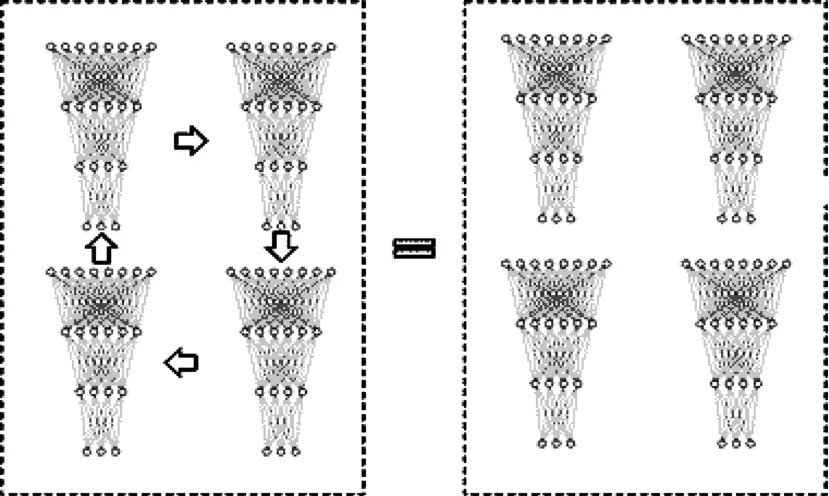
图4 多个相同网络权值自适应加权过程

假设W1i为模型N1′的第i层的权重参数，W2i为模型N2′的第i层的权重参数，则加权融合后模型N2′的第i层的权重参数为

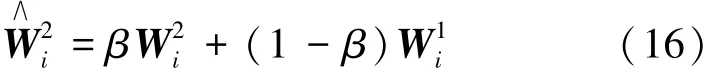
其中β（0＜β＜1）为自适应加权融合参数，即

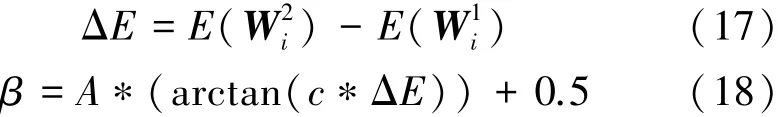
其中A和c为超参数。

最后，训练完成之后，从多个相同网络模型中选取性能最优的子网络模型。

3 实验与分析

为了分析和验证本文所提方法的有效性，在CIFAR10、CIFAR100 和 ILSVRC⁃2012 ImageNet标准分类数据集上对几种常用的卷积神经网络模型（VGG16，ResNet56，MobileNetV2，ResNet50）进行实验。其中 CIFAR10和 CIFAR100数据集，包含50 000张训练图像和10 000张测试图像。CIFAR10数据集中图像类别为10类，CIFAR100数据集中图像类别为100类。ILSVRC⁃2012 ImageNet是规模庞大的数据集，其中包含128万张训练图像和5万张验证图像，图像类别为1 000类。

3.1 实验环境

深度学习框架为Pytroch，操作系统为Ubuntu 18.04，CPU 为 Intel@Veon（R） E5⁃1640 v4，运行内存为 8 GB，GPU 为 NVIDIA GeForce GTX2080Ti，GPU显存为11 GB。

3.2 性能指标

浮点运算量（Float Points Operations， FLOPs），表示运行该模型需要的浮点数运算量。此外对于CIFAR10、CIFAR100 和 ILSVRC⁃2012 ImageNet数据集均采用Top⁃1的分类预测准确度作为网络模型的性能指标。

3.3 CIFAR⁃10／100 实验设置

在CIFAR⁃10／100数据集上，通过随机裁剪、随机拉伸和随机旋转进行数据增强，把输入图像的尺寸大小统一为32∗32∗3。在利用双DDPG算法学习全局规模系数和全局偏差系数过程中，epoch为300。在多个相同网络并行训练过程中，优化器是随机梯度下降和梯度集中［27］，epoch为 90，余弦退火调整学习率，每一子网络的初始学习率从［0.1，0.01］区间内随机取值，权重衰减率从［1e－4，2e－3］区间内随机取值，c＝600，A＝0.2。

3.4 ILSVRC⁃2012 ImageNet实验设置

在ILSVRC⁃2012 ImageNet数据集上，输入图像的尺寸大小统一为224∗224∗3。数据增强方法与CIFAR⁃10／100数据集的数据增强方法相同。在利用双DDPG学习网络模型每一个卷积层的全局规模系数和全局偏差系数中，epoch为300。在多个相同网络并行训练过程中，优化器是随机梯度下降和梯度集中［27］，epoch为 60，学习率的调整策略为余弦退火，每一子网络的初始学习率从［0.1，0.01］区间内随机取值，权重衰减率从［1e－4，1e－3］区间内随机取值，c＝500，A＝0.3。

3.5 实验结果与分析

3.5.1 CIFAR10数据集

为了验证本文所提方法的通用性和有效性，本文对主流的深度神经网络模型 ResNet56、VGG16、MobileNetV2进行结构化剪枝，并与现有的先进方法PF［6］、 HRank［9］、 GAL［28］、 AMC［21］、 DCP［29］、LEGR［14］、ABC［22］、MDP［30］、SSS［19］进行对比，证明本文提出方法的有效性。结果如表1所示。

对于ResNet56网络而言，该网络模型由残差模块组成，其包含55个卷积层。从表1可以看出，该方法得到的剪枝后的模型在FLOPs小于其他方法的情况下，网络模型性能明显优于其他方法。最后还统计了剪枝后网络模型中各个卷积层的剪枝率，如图5所示。

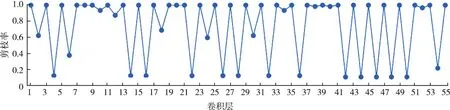
图5 在CIFAR10数据集上ResNet56每一层的剪枝率

对于VGG16网络而言，该网络模型包含3个全连接卷积层和13个顺序卷积层。如表1所示，HRank方法在FLOPs降至73.7 M时，在CIFAR10测试数据集上的分类准确度为91.23%。而该方法在FLOPs降至78 M时，在CIFAR10测试数据集上的分类准确度为92.34%。

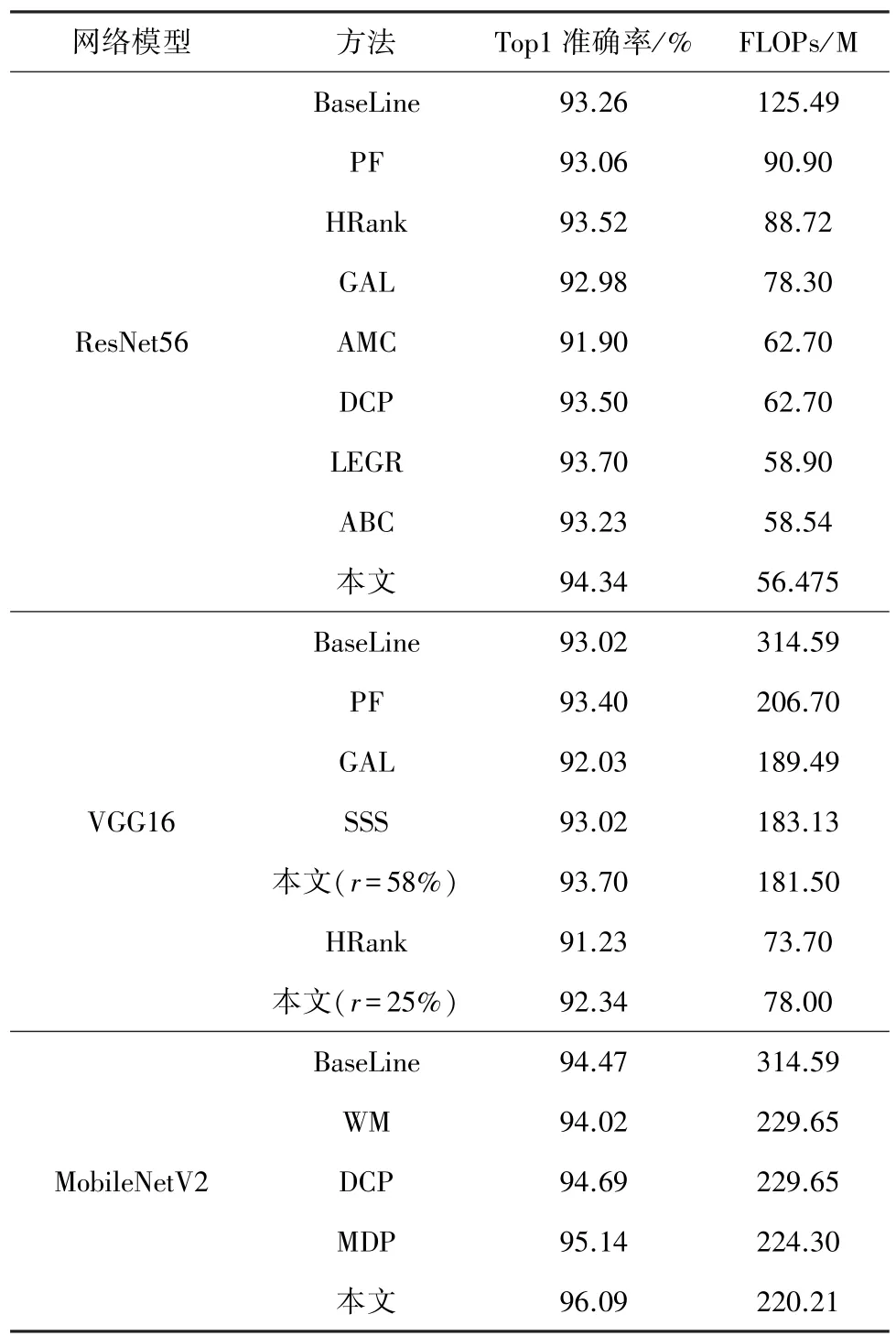
表1 不同剪枝方法在CIFAR10数据集上的对比结果

MobileNetV2是紧凑型网络，结构为基于分离卷积的倒置残差结构。网络模型中包含52个卷积层。由于MobileNetV2的计算成本极小，对其进行剪枝是一件极具挑战性的任务。尽管如此，本文所提出的方法是在减少30%FLOPs的条件下，通过相同多网络并行训练使得模型的精度增至96.09%。本文方法的效果明显优于所对比的几种先进方法。

3.5.2 CIFAR100数据集

在CIFAR100数据集上对ResNet56网络进行剪枝，并与具有先进代表性的方法 AMC［21］、LEGR⁃EA［14］以及 SFP［18］进行对比，如表 2 所示。由表2可以看出，通过本文的方法把标准的ResNet56网络的FLOPs降至63.8 M时，网络的性能只降低了0.68%。并且通过定量对比，发现该方法依旧优于所对比的主流方法。图6为剪枝后网络模型中各个卷积层的剪枝率。通过对比图5和图6，发现对于同一个网络，在FLOPs相近似的情况下，基于不同的数据集，每一层的剪枝率是不相同的。

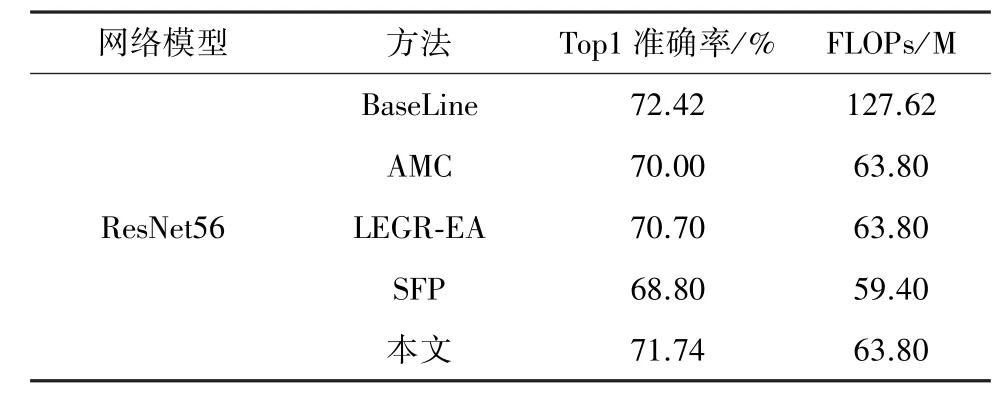
表2 不同剪枝方法在CIFAR100数据集上的对比结果

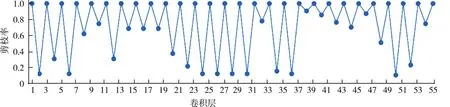
图6 CIFAR100数据集上ResNet56每一层的剪枝率

3.5.3 ImageNet数据集

表3为本文提出的剪枝方法与 HRank［9］、ThiNet⁃30［20］、MetaPruning［31］、ABC［22］等现有先进算法在大规模数据集ImageNet上的实验结果。模型的FLOPs由4.136 G减少至0.927 G，模型精度则减少至70.73%。通过表3可以看出该方法在大规模数据集上面的表现仍然优于现有的先进方法。

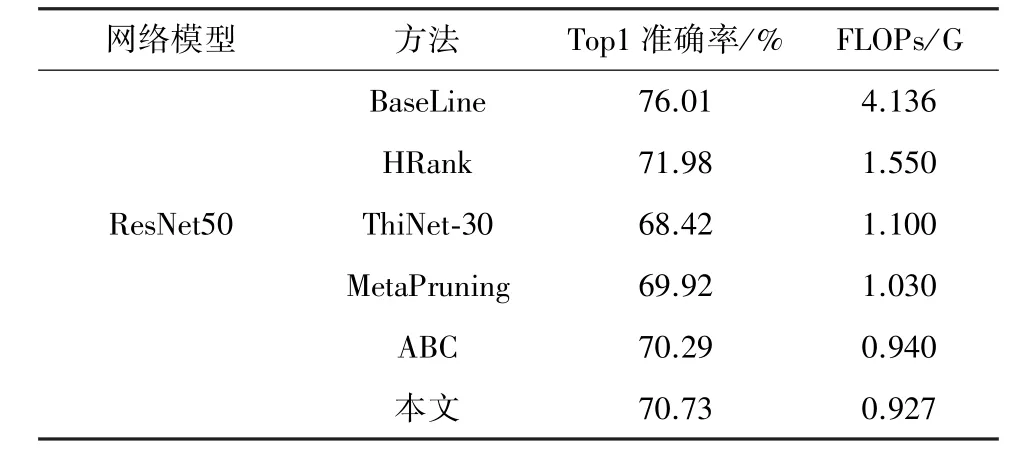
表3 不同剪枝方法在ImageNet数据集上的对比结果

4 结束语

本文提出了一种基于双DDPG的全局自适应滤波器剪枝方法。首先计算出滤波器权值的信息熵，并作为该滤波器在当前层中的局部重要性得分。接着，基于双DDPG算法学习出每一层的全局规模系数和全局偏差系数，从而计算出卷积层中每个滤波器的全局重要性得分。根据全局重要性得分进行剪枝，得到结构最优的子网络。最后为了恢复剪枝后得到子网络的性能，采用了基于权值自适应加权的多个相同网络联合并行训练。实验结果表明，本文提出的方法在保证网络性能良好的同时，能够有效减少模型浮点计算量。在一些数据集上，子网络模型的性能表现甚至超过了原始网络模型。同时，通过该方法得到的剪枝后的模型具有较强的易用性，不需要特殊的硬件或软件库进行辅助，可以轻松地部署在可移动设备上或者移植到下游的计算机视觉任务中。下一步将尝试把模型剪枝与其他模型压缩方法（如量化、神经架构搜索）相结合。