基于平行光管与二维旋转平台的长焦相机内参标定*

杨文广，高 丹，罗子娟，钱惟贤

(1.南京理工大学 电子工程与光电技术学院·南京·210094；2. 上海航天控制技术研究所·上海·201109;3. 中国电子科技集团公司第二十八研究所·南京·210007)

0 引 言

光学遥感技术是一种获取对地观测信息的重要手段，光学遥感的数据来源则以长焦相机拍摄到的图像为主[1]。相机标定是视觉测量初始阶段的一项关键技术，标定精度将直接影响图像三维测量[2]、图像匹配[3]等衍生技术的准确性。目前，国内外提出了大量相机标定算法[4-5]。根据标定物状态，对于相机的标定可分为二维标定[6]和三维标定[7]两种。其中，二维标定物主要用于对短焦镜头进行标定，常见的算法包括径向约束两步法[8]和平面标定法[9]两种。但是，对于长焦镜头而言，二维标定板放置过近，会导致成像模糊，造成较大的误差；二维标定板放置较远，则会导致图像分辨率不足，无法较好地识别角点。相对而言，三维标定物能够较好地分布于图像整个平面。但是，三维标定物的制作与维护较为困难，存在较大的使用局限性，实验的复杂性也较高。

传统的长焦镜头标定方法主要针对标定物或离焦图像设计标定方案。孙楠等[10]通过大型十字标靶对相机进行了标定。Wang等[11]提出了一种可应用于失焦彩色相机校准的标准尺寸彩色编码模式，将特征点编码到相位而不是强度中，以便于从模糊图像中提取特征点。文献[12]通过使用圆形相移图案对特征点进行编码，需通过精确拟合得到第一个截断周期处的亚像素坐标，且没有考虑伽马非线性误差对相位造成的影响。

针对二维标定靶标的缺点，本文通过在平行光管焦平面处放置透过式靶标，可使远焦相机拍摄到清晰的靶标图片，并结合精确二维旋转平台搭建了一套相机内参标定系统。二维旋转平台与相机固连，通过旋转使得靶标成像分布在整个相机视场中。通过两幅图像对应点之间的对极约束以及旋转平台对相机旋转平移运动的精确计算，使用最优化算法，实现远焦情况下相机内参的精确标定。相比传统方法，本文算法采用二维标定靶标，简化了实验条件。相比基于离焦图像设计的标定方案，本文通过对比实验验证了算法的优良性以及实用性。

1 相机标定方案设计

1.1 相机标定原理

三维空间点的成像原理通常可用针孔模型表示[13]

(1)

式中，[uv1]T为图像坐标系下目标坐标的齐次表示，s为归一化系数，[XYZ1]T为空间坐标系下目标坐标的齐次表示。H表示相机内参，R为3×3的旋转矩阵，T为3×1的平移矢量，R、T两者共同构成了3×4的相机外参矩阵[R|T]。在成像模型中，[R|T]的值与空间坐标系的选取有关。当空间坐标系发生变化时，[R|T]也会相对应地发生变化。H可以表示为

其中，[u0,v0]为主点坐标。在理想情况下，其位于图像中心点；sxy为倾斜因子，一般默认为0；[fx,fy] 为等效焦距，其理论值为

(2)

式中，f为镜头焦距，[dx,dy]分别为图像在x方向和y方向上的像元尺寸。由内参各个元素的定义可知，内参的取值只与相机本身的状态有关，而与外部环境无关。因此，在使用相机前对相机内参进行标定求解，具有重要的意义。

1.2 平行光管的性质

平行光管的结构原理如图1所示。根据几何光学原理，无限远处的物体经过透镜后将成像在焦平面上；反之，从透镜焦平面上发出的光线在经过透镜后将成为一束平行光。如果将一个物体放置在透镜的焦平面上，那么它将成像在无穷远处。基于这一特征，当在平行光管透镜的焦平面上放置一块带有特征图案的靶标时，长焦相机便可以清晰地捕捉到图案特征的成像。

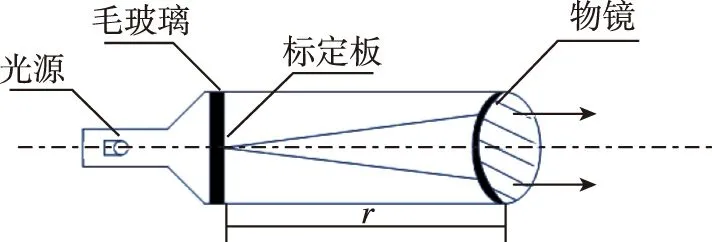
图1 平行光管的结构原理Fig.1 Structure principle of parallel light tube

如图1所示，毛玻璃可使靶标被均匀照亮。由靶标上的每一点发出的光在经过物镜后，都成为了一束平行光，靶标上的图案也将成像在无限远处。这样，当在透镜后方放置长焦相机时，靶标相当于一个距离无限远的目标。通过调节靶标与焦平面的位置，便可使相机对靶标清晰成像。

1.3 实验平台搭建

本文在光学平台上搭建了如图2所示的实验平台。

图2 相机标定平台Fig.2 Camera calibration platform

实验平台主要分为两个部分，左边为平行光管，内部放置了用于标定的透过式标定板，光源为自然光或普通灯光。右边为成像模块，相机架设在经纬仪上，并与经纬仪保持固连。相机旋转角度由经纬仪读数给出。在转动过程中，应尽可能使棋盘格成像分布于整个成像画面上。

2 标定模型

2.1 相机与转台旋转模型

将相机固定于标准的二维旋转平台(以电子经纬仪为例)，通过旋转平台绕中心的旋转来实现相机的间接绕中心旋转。旋转前后，相机位置的变换可由图3进行描述[14]。

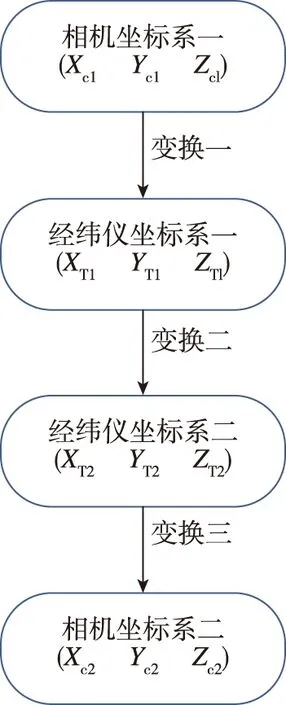
图3 相机与转台旋转坐标系的变换流程Fig.3 The transformation process of camera and turntable rotating coordinate system

任意两个坐标系之间的变换关系均可由旋转加平移实现。在图3中，由于相机与旋转平台固连，变换一和变换三为一个互逆过程，其过程可用一个旋转平移矩阵[Rct|Tct]表示。

变换二可认为由转台分别绕转台坐标系的X,Y两轴旋转变换而来，旋转角度可由经纬仪读数获得，变换关系如图4所示。

图4 转台旋转模型Fig.4 The model of turntable rotates

在图4所示的转台旋转模型中，Y轴、YT轴、Z轴、ZT轴均在一个平面上。X、Y为经纬仪的旋转轴。在旋转过程中，XT轴和X轴始终重合，定义从坐标原点向坐标系正方向看时的逆时针方向为旋转正方向。在转台中，任意位置的经纬仪坐标系都可以用两个参数表示，分别是垂直角度θ以及水平角度λ。其中，θ为ZT轴和Y轴负方向的夹角，λ为X轴与零位时的X轴的夹角。可以看出，当θ不为90°时，坐标系OT-XTYTZT在旋转时是围绕Y轴而非YT轴。因此，首先要将OT-XTYTZT坐标系绕X轴旋转至与OT-XYZ坐标系重合的位置，再将其绕Y轴旋转。最后，再将OT-XTYTZT绕X轴旋转至对应的位置，该过程可以用图5所示的流程图表示。

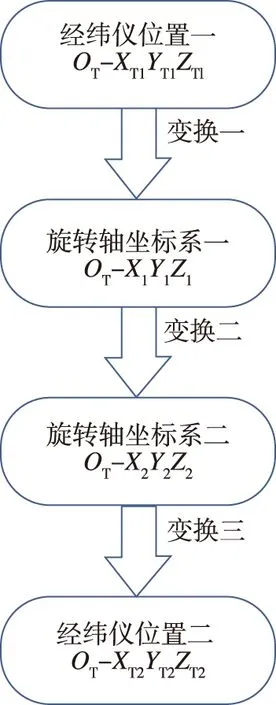
图5 经纬仪旋转坐标系变换流程Fig.5 The transformation process of theodolite rotating coordinate system

其中，OT-XT1YT1ZT1、OT-XT2YT2ZT2、OT-X1Y1Z1和OT-X2Y2Z2分别为旋转前后的经纬仪坐标系和旋转轴坐标系。对于任意两个不同位置的经纬仪，设其读数分别为(θ1,λ1)及(θ2,λ2)，则对于变换一，即坐标系OT-XTYTZT绕XT轴旋转(90-θ1)，可以用旋转矩阵表示为

(3)

变换二可以看作坐标系OT-X1Y1Z1绕Y轴旋转(λ1-λ2)，可以表示为

(4)

变换三，即坐标系OT-XTYTZT绕XT轴旋转(θ2-90)，可以表示为

(5)

综合式(3)、式(4)、式(5)，可以得到任意两个位置的经纬坐标系之间的变换关系

RT=RT3RT2RT1

(6)

本文主要应用于长焦相机的标定，在平行光管作用下，可认为靶面与相机无穷远。在此情况下，相机的平移不影响最终的成像效果[15]。因此，可认为相机坐标系与经纬仪坐标的原点重合，即两者之间不存在平移关系。由此，可以得到任意两个位置的相机坐标系之间的变换关系

(7)

其中，Rct为相机与经纬仪之间的固定旋转变换参数。该值虽然不可知，但作为固定值可以与内参一起进行优化求解。由于只考虑旋转，该值为模型引入了3个自由度。RT为运动前后经纬仪的旋转矩阵，可由经纬仪读数计算而得。

2.2 长焦相机标定模型

经过平行光管的作用，棋盘格上所有的点相对于相机而言均可被认为是无穷远的点。假定空间点坐标在相机坐标系下的坐标为P=[X,Y,Z]T。相机的运动由旋转矩阵R和平移矩阵T表示，根据式(1)，空间点的像素坐标在旋转前后可以表示为[16]

s1p1=KP
s2p2=K(RP+T)

(8)

式中，s1、s2分别表示相机在旋转前后位置上的归一化系数，p1和p2分别表示在相机旋转前后空间点的像素坐标的齐次表示，K为相机内参。

对于远焦相机，可以认为对于同一张图片，棋盘格上所有的点的深度信息相同。对于棋盘格上点的世界坐标，可以表示为

P=s1K-1p1

(9)

旋转后的成像方程可以写为

s2p2=K(R(s1K-1p1)+T)

(10)

对于无穷远点的目标，相机的平移不影响图像的成像。因此，式(10)的平移量可以被忽略，式(10)可以简化为

sp2=K(R(K-1p1))

(11)

其中，s=s2/s1为合并后的归一化系数，由此可得到目标函数

(12)

其中，pi(i=1,2,3,…)为旋转前后匹配点的棋盘格图像坐标。K表示相机内参，R为旋转前后相机的旋转矩阵，由1.2节的旋转模型进行表示。利用Levenberg-Marquardt算法[17]，以式(12)为目标函数，待解参数为内参以及相机与经纬仪之间的固定变换参数。在这种情况下，待解参数的数目是固定的，不会随着标定图像的增加而增加。对参数进行优化求解，即可求解出相机内参。

3 实验结果与分析

3.1 本文算法实验结果

本文使用的旋转平台为一光DT402L型电子经纬仪，以Basler黑白工业相机为采集设备，相机分辨率为2048pixel×2048pixel，相机像素尺寸为5.5μm×5.5μm 。镜头采用vilber lourmat的变焦镜头，焦距变换范围为12.5～50mm。首先，在不同焦距下通过平行光管对透过式棋盘格进行成像，对不同焦距下的相机内参进行标定，并计算图像点的重投影残差。图像残差用E表示

(13)

本文在不同焦距下采集了棋盘格图像，部分图像如图6所示。

由图6可知，经过平行光管的折射，不同焦距下的棋盘格图像角点均清晰可见，检测到的角点误差较小，满足标定精度。

图6 棋盘格图像采集(a)焦距为12.5mm(b)焦距为15mm(c)焦距为20mm(d)焦距为30mm(e)焦距为50mmFig.6 Checkerboard images (a) The focal length is 12.5mm (b) The focal length is 15mm (c) The focal length is 20mm (d) The focal length is 30mm (e) The focal length is 50mm

根据第2节的模型，对图像进行标定，不同焦距下的标定结果如表 1所示。

表1 本文算法内参标定结果与重投影残差

3.2 对比算法实验结果

将本文与实验室内离焦相机的标定方法进行对比实验[18]，相机传感器、镜头均保持不变。标定板采用普通圆形图案，标定靶距离相机的距离约为2m，在不同焦距下采集到的图像如图7所示。在实验过程中，依然可通过调整焦距对靶标进行拍摄。标定结果如表2所示。

表2 对比算法内参标定结果与重投影残差

由图7可知，当焦距较小时，相机采集到的图像较为清晰，而当焦距较大时，图像占比变大，标定板模糊，不容易检测到角点，也无法采集多幅图像并完成标定。

图7 不同焦距下采集到的圆形图像标靶(a)焦距为12.5mm(b)焦距为15mm(c)焦距为20mm(d)焦距为30mm(e)焦距为50mmFig.7 Circular calibration plate (a) The focal length is 12.5mm (b) The focal length is 15mm (c) The focal length is 20mm (d) The focal length is 30mm (e) The focal length is 50mm

由表2可知，当焦距增加到30mm以上时，采集到的图像已无法进行标定。

3.3 结果分析

根据相机内参的物理意义可知，本文选取相机的内参理论值为fx=f/5.5(μm)，fy=f/5.5(μm)，u0=1024，v0=1024。其中，u0、v0为内参的主点坐标。由于相机工艺、靶面距离等实际原因，实际结果与理论结果存在偏差，但理论值仍具有参考价值，这也是标定的意义。根据表1的结果，本文算法的标定结果均与理论值存在可比性，说明优化结果并不是局部极值。本文标定结果的重投影误差约为0.5个像素，误差高于近焦情况下张正友算法标定误差，且随着焦距增加，重投影误差随之增大。这是由于焦距增大，相机的视场随之减小，反应在图像上，则表现为棋盘格尺寸变大，角点所占像素随之变大。在相同的情况下，棋盘格角点的检测误差也会随之增大。即便如此，本文算法的最大误差约为0.5个像素，证明了算法的可行性。

相比于离焦相机的标定方法，由图6和图7的对比实验图可以看出，当焦距增加到一定程度时，离焦图像已基本丧失所有的图像数据。由表1和表2可知，当焦距较小时，离焦相机标定方法的精度略高于本文算法，这是由于转台的引入增加了数据的误差，并且在模型推导中，忽略了相机平移量。当焦距逐渐增加，忽略平移量对标定的影响越来越小，标定精度仍然保持得较好。而在离焦情况下，图像的模糊度越来越高，圆心位置误差越来越大，标定的误差也越来越大。当焦距在30mm以上时，算法已无法正确检测圆心的位置，标定失败。

4 结 论

本文提出了一种基于二维旋转平台和平行光管的远焦相机内参标定模型，通过一对固定的坐标系旋转平移变换与逆变换，将相机坐标系的非绕中心旋转转换为旋转平台的绕中心旋转变换，实现了相机变换矩阵的精确计算。通过平行光管对棋盘格的处理，使得长焦相机能够捕捉到精确的特征点信息，由此实现在实验室内对长焦相机内参的精确标定。相比采用离焦相机的标定办法，本文算法在焦距越长时，标定精度越好，而且成功率也相对较高。实验结果表明，标定后的内参符合内参的物理意义，角点重投影坐标误差约为0.5个像素，由此说明本文的标定方法具有较高的精度。