A low noise,high fidelity cross phase modulation in multi-level atomic medium*

Liangwei Wang(王亮伟) Jia Guan(关佳) Chengjie Zhu(朱成杰)Runbing Li(李润兵) and Jing Shi(石兢)

1Laboratory of Artificial Micro-and Nano-structures of Ministry of Education and School of Physics and Technology,Wuhan University,Wuhan 430072,China

2School of Physics Science and Engineering,Tongji University,Shanghai 200092,China

3School of Physical Science and Technology,Soochow University,Suzhou 215006,China

4Collaborative Innovation Center of Light Manipulations and Applications,Shandong Normal University,Jinan 250358,China

5State Key Laboratory of Magnetic Resonance and Atomic and Molecular Physics,Wuhan Institute of Physics and Mathematics,Chinese Academy of Sciences,Wuhan 430071,China

Keywords: phase modulation,electromagnetically induced transparency,nonlinear Kerr phase shift

Quantum computers and quantum information processing technologies are expected to be the critical technique for revolutionizing information science.[1-4]Effective manipulation of photons at single-photon intensity is essential for the next-generation photon communication.[5]So far, based on nonlinear Kerr cross-phase modulation caused by magnetic field and electric field,many schemes used to realize quantum phase gates have been proposed.[6-10]In general,the nonlinear cross-phase modulation in passive media is weak and requires a long propagation distance in solid media.[11]However, in atomic gases, nonlinear effects can be enhanced by choosing different energy levels and transition pathways. Based on these features, strong nonlinear effects can be achieved by using electromagnetic induction transparency (EIT)[12-17]or weakly driven active Raman gain (ARG)[18-28]technologies. In particular, Artoniet al.proposed a novel phaseby-phase control mechanism to achieve broadly tunable light phase shifts.[29]Recently, Sunet al.proposed a method to realize large polarization-dependent cross modulation between incident weak lights even at the few-photon level.[30]We have also developed a polarization selective Kerr phaseshifting technology,[31,32]in which a weak phase-control field can be used to achieve rapid phase or polarization control and achieve vector gate operation with polarized light in an atomic medium.

For any technologically viable Kerr-effect-based phase gate, three important characteristics must be met. These are lager phase shift, lower loss and no additional phase noise.Theπnonlinear Kerr phase shift has been observed in our recent studies using ARG[19]and EIT[33]methods, respectively. However,the other two features are unattainable independently with weakly driven EIT-based methods and ARGbased methods. In EIT methods, the fundamental problem with weakly driven EIT schemes is that the process operates in an absorption mode and the signal wave suffers from significant attenuation and inherently lossy. This influences the efficiency to check the photon numbers and deceases the fidelity of the quantum operations. In ARG methods, the process operates in a stimulated radiation mode and the additional photons participate into the signal wave. This is harmful for the quantum information processing due to the quantum clone effect.

In this paper, we present a hybrid scheme of cross phase modulation based on electromagnetically induced transparency(EIT)and active Raman gain(ARG)in a multi-level atomic medium. The signal wave is propagating in the EIT window and modulated by the phase-control field,in which an ARG process is synchronously applied. The experimental results show thatπradian nonlinear Kerr phase shift of signal light relative to a reference light is observed when the signal light is modulated by a phase control field with low light intensity. The linear and the third-order absorption of the signal light can be eliminated by the stimulated Raman process,and the phase noise of the signal light can also be ignored when the phase control light is applied in this hybrid scheme. Our theory matches the experimental results very well.

We consider an ensemble of life-broadened six-level Mtype85Rb atoms system as shown in Fig. 1. The signal field with Rabi frequencyΩScouples|1〉 ↔|4〉transition with one-photon resonance,and also|3〉↔|5〉transition with onephoton detuning 3.0 GHz. The coupling field with Rabi frequencyΩCcouples|3〉↔|4〉transition,where the two-photon resonance is satisfied between the signal light and the coupling light. The pumping field with Rabi frequencyΩPcouples|2〉↔|5〉transition,in which the two-photon resonance is also satisfied between the signal light and the pumping light.To realize aπKerr phase shift, the phase-control field with Rabi frequencyΩPhdrives the transition between states|3〉and|6〉.

Fig. 1. The scheme of energy levels for cross phase modulation. The signal field couples|1〉↔|4〉transition with one-photon resonance,and also|3〉↔|5〉transition with one-photon detuning of 3.0 GHz.The coupling field couples|3〉↔|4〉transition while the pumping field couples|2〉↔|5〉transition,where the two-photon resonance is synchronously satisfied. The phase-control field drives|3〉↔|6〉transition. Here,ΩP,ΩS,ΩC and ΩPh denote the Rabi frequencies of the pump,signal,control and phase control fields,respectively.

Under the rotation wave approximation,the equations of motion for atomic state amplitudesAjin a six-level atomic system can be written as

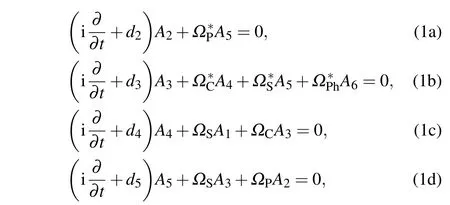
withNabeing the atomic density,ε0the vacuum dielectric constant,andcthe light speed in vacuum.

Equations (1) and (2) can be solved analytical using the following asymptotic expansion:

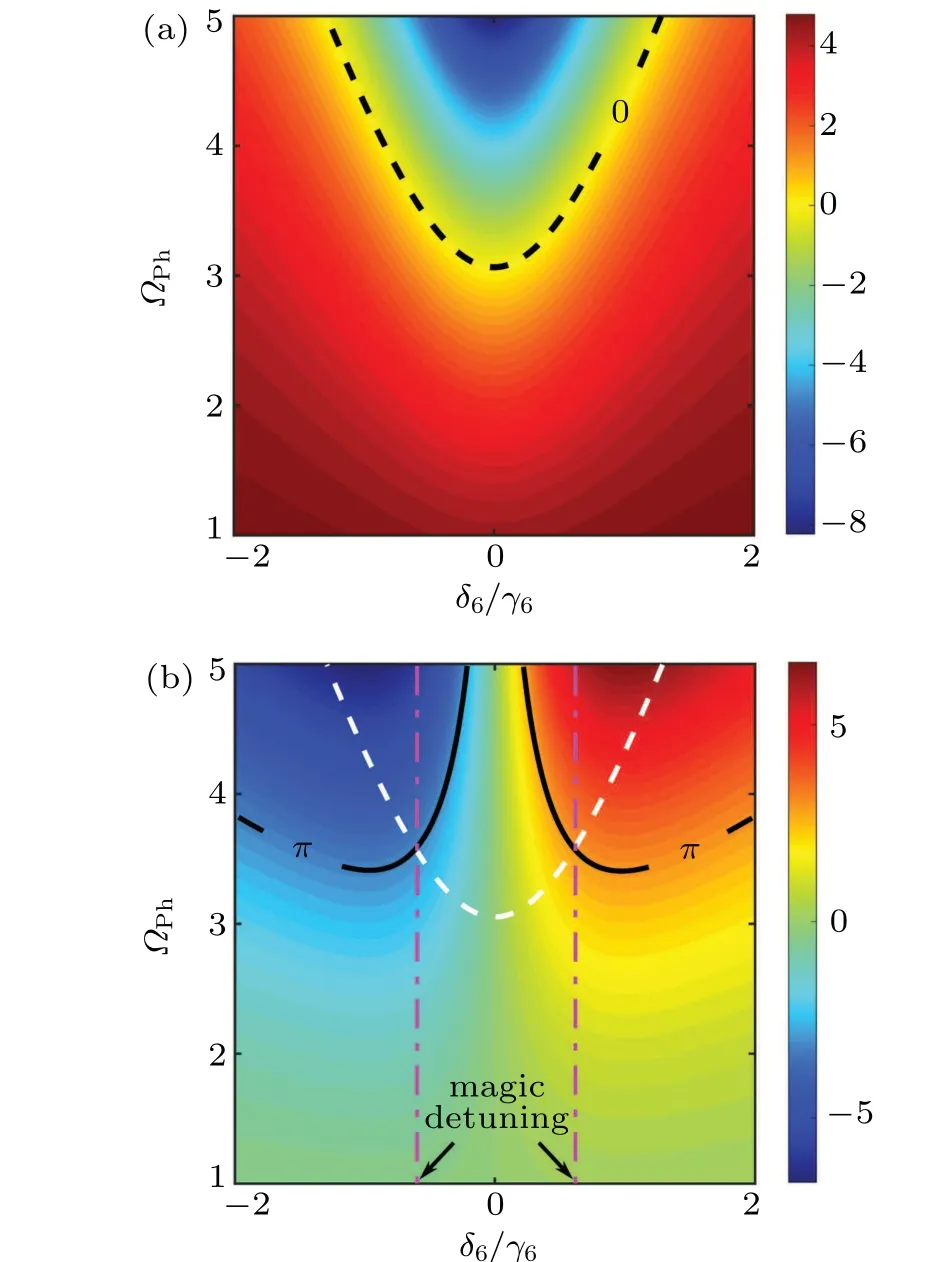
Fig.2. The total absorption/gain αtot (a)and the phase shift φtot (b)as functions of the phase-control field Rabi frequency ΩPh and the normalized detuning δ6/γ6,respectively. The black dashed curve in(a)denotes αtot =0,and the black solid curves in (b) denote φtot =±π. The pink dash-dotted lines indicate the magic detunings where a π phase shift can be achieved with zero loss or gain.

For a conventional N-type EIT scheme, the signal field undergoes strong attenuation originated from the linear and nonlinear absorption to obtain large phase shift. With the ARG branch, however, the gain originated from the stimulated Raman process compensates the absorption of the signal field during its propagation. Thus, the absorption or gain of the signal field can be eliminated by adjusting specific intensity and detuning of the signal field. To show this point, we plot the total loss/gainαtot=αL+αNL[Fig. 2(a)] and phase shiftφtot=φL+φNL[Fig. 2(b)] of the signal field as functions of the phase control field Rabi frequencyΩPhand the detuningδ6, respectively. Here, the atomic density is chosen as 6×1011cm−3, and other system parameters are given byδ5=3 GHz,δ3=δ4=0 Hz,γ3=200 kHz,γ4=γ5=γ6=300 MHz,ΩP=20 MHz,ΩC=15 MHz andL=7.5 cm. Obviously,the absorption or gain can be eliminated(i.e.,αtot=0)by choosing a set of specific phase control field Rabi frequency and detuning (see the black dashed curve) as shown in Fig.2(a). Moreover,there exist two“magic”detunings denoted by the pink dash-dotted lines in Fig. 2(b), where aπphase shift(i.e.,φtot=±πindicated by the black solid curves)for the signal field can be achieved without any absorption or gain.

To verify the above theoretical results, the experiments are conducted in a six-level rubidium atom system shown in Fig. 3(a). The length and the diameter of this85Rb vapor cell are 7.5 cm and 2 cm, respectively. It is filled with 933 Pascal Neon buffer gas and also shielded from ambient magnetic fields under three layers of µ-metal. The temperature of this atomic gas is about 320 K and the atomic density is about 6×1011cm−3. A weak magnetic field with an intensity of 100 mG is applied along the propagation direction of the signal field. Thus, the atomic states of this sixlevel system is chosen as|1〉 ≡|5S1/2, F= 2, mF=−2〉,|2〉≡|5S1/2, F=2, mF=0〉,|3〉≡|5S1/2, F=3, mF=−1〉,|4〉≡|5P1/2, F=2, mF=−2〉,|5〉≡|5P1/2, F=2, mF=−1〉,and|6〉≡|5P3/2, F=4, mF=−1〉. The linearly polarized signal field and left-circularly polarized coupling(pump)field are collected together by a beam splitter(BS),and propagate along the direction of the magnetic field. Then,the signal field is separated into two lights,where one is the signal field while the other one is utilized as the reference field. After the interaction with the atom, they are combined together by using another beam splitter (BS) to build the optical Mach-Zehnder interferometer. We set a small angle of less than 1°between the pump(coupling)and signal fields so that they are physically separated at a distance of about 1 m from the exit of the vapor cell. To introduce a Kerr phase shift,we inject a weak linear polarized phase-control field with a 3 mm beam diameter and the signal field that are overlapped with opposite propagating directions. In our experiment,the two-photon resonant condition is satisfied between the signal field and the coupling field to obtain the maximum intensity of the signal field.

In the experiment, the coherent fields are generated by an acousto-optic modulator as shown in Fig. 3(b). The coupling field is locked on the transitions between states|3〉and|4〉of the85Rb atoms via a saturated absorption spectroscopy,and modulated by the acousto-optic modulator with the offset frequency 3.04 GHz. The signal field is generated by the+1 order diffracted light of the AOM. The pumping field is generated by the 2×(+1) order diffracted light of the AOM with the double-pass configuration, which is amplified by a tapered amplifier. The strong coupling field with 6 mW intensity and 3 mm beam diameter and the pumping field with 12 mW intensity and 3 mm beam diameter drive|3〉↔|4〉and|2〉↔|5〉transitions,respectively. The vertical-polarized signal field with 5µW intensity and 1 mm beam diameter drives|1〉↔|4〉and|3〉↔|5〉transitions simultaneously. Thus the M-type scheme is formed by combining the EIT and ARG schemes. The phase-control field coupling the states|3〉↔|6〉is applied to observe the cross phase modulation in this hybrid scheme.

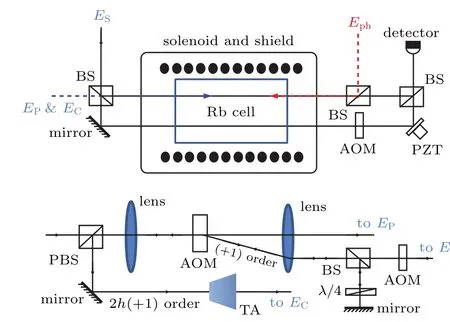
Fig. 3. (a) The experimental setup. (b) The generation of coherent fields. The 85Rb vapor cell is shielded from the ambient magnetic field.An about 100 mG magnetic field is generated by the solenoid, which provides a quantum axis for the atoms. The Mach-Zehnder interferometer is used to observe the nonlinear phase shift.

In the three-levelΛ-type EIT, the signal light will transmit the medium when the two-photon resonance conditions are satisfied. In the experiment, the coupling field resonantly drives the transition between states|3〉and|4〉. Carefully adjusting the intensity and one-photon detuning of the pump field,the signal field is then passed through the medium without any loss when the two-photon resonance condition is satisfied. In this scheme,the width of the EIT window is nearly 200 kHz as shown in Fig.4(b)(see the red curve). However,in the five-level M-type medium, the signal field is amplified due to the active Raman gain process when the pump field is present. The intensity of the signal field is increased by 3 times, and its spectrum width is about 202 kHz as shown in Fig.4(b)(see the black curve). Due to the third-order absorption demonstrated in Eq.(5b),the intensity of the signal field decreases as the intensity of the phase-control light increases in this six-level system. In Fig.4(a),the intensity of the signal field is plotted against the phase-control field. As the power of phase-control field increases, the signal field intensity decreases greatly due to the third-order absorption. By carefully adjusting the system parameters,we can obtain the same absorption for the EIT-type system without the phase-control field and the M-type system with the phase-control field. In Fig. 4(a), the red curve indicates the absorption for the EITtype system,while the black curve denotes the absorption for the M-type system. The transmission rate of the signal light can be calculated by the expressionηL=exp[−2kSIm(χS)L].Here theπnonlinear phase shift can be written into the signal field when the phase-control field is applied as demonstrated in Eq. (5). Similar to our previous works,[19,33]the nonlinear Kerr phase shift is studied by employing an optical Mach-Zehnder interferometer. Theπnonlinear phase shift is observed in this hybrid scheme when the power of the phasecontrol field is only about 0.5 mW. Correspondingly, the intensity of the phase-control field is nearly 7 mW/cm2.

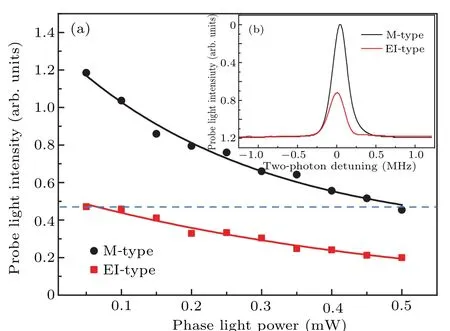
Fig. 4. (a) The intensity of the signal field plotted against the phasecontrol field. It is decreased, due to the third-order absorption, with increasing the power of phase-control light. (b) The intensity of the signal field plotted as a function of the two-photon detuning.

Next, we examine the frequency spectrum of the signal laser,which was measured by a microwave spectrum analyzer using the beat signal. The signal field is separated into two parts after the PBS and half-wave plate, one is signal field and the other is the reference field shown in Fig.3. After two AOMs are used to shift the frequency of the reference field,the signal field and the reference field are combined each other using a beam splitter. In Fig.5(a),we show the beat note signal.The red curve is the beat note spectrum between the signal field and reference field when the coupling field is present(see the EIT-type system), while the blue curve denotes the case of coexistence of the coupling field and pumping field (i.e.,the M-type system). The widths of the beat note signals are 31 kHz and 53 kHz for the EIT-type and M-type schemes,respectively. The beat note spectrum is also measured when the phase-control light is present. When the power of the phasecontrol light is about 0.5 mW(see the black curve), its width is about 32 kHz. In Fig.5(b),we also show the widths of the beat note signals for the different powers of the phase-control light in the M-type scheme. Obviously,its widths is decreased greatly as the power of the phase-control field increases.

Fig.5.(a)The beat note signals for the EIT-type system(red curve),the M-type system without the phase-control field(blue curve),and the Mtype system with the phase-control field(black curve). (b)The widths of the beat note signals versus the intensity of the phase-control field.Its width is close to that of EIT when the power of the phase-control light is about 0.5 mW,where a π nonlinear phase shift is achieved.

We should point out that the intensity and frequency of the signal photons is very important in the quantum computers and communications.In Fig.4,we can see that the intensity of the signal light is attenuated not only in the EIT-type scheme but also in the M-type scheme when the phase-control field is applied.In this phase operation,the intensity of the signal field without the phase-control light in the EIT scheme is required to be the same as its intensity with the phase-control field in the M-type scheme. At the same time, the width of the beat note signal with the phase-control field in the M-type scheme must be the same as its width without the phase-control field in the EIT-type scheme(see Fig.5). Then,one can obtain the low noise and lossless cross phase modulation in this hybrid scheme.

In summary, we have developed a hybrid scheme for realizing strong cross phase modulation based on both electromagnetically induced transparency and active Raman gain in a multi-level atomic medium. By choosing specific system parameters, we show that the linear and the third-order absorption can be eliminated simultaneously via the Raman gain process in such a system. The cross phase modulation with low loss rate and very weak noise is demonstrated in a roomtemperature85Rb vapor. We also show that the phase noise of the signal field can also be ignored when the phase control field is applied in such a hybrid scheme.