基于证据推理的低等级农村公路路段安全风险评价

汤天培，王海波，陶阳晨，徐思源，仲小飞

(1.南通大学 交通与土木工程学院，江苏 南通 226019; 2.中设设计集团股份有限公司)

1 前言

截至2020年底，中国农村公路总里程达438.2万km，占公路总里程的84.3%，等级公路比例达到95%以上，为农村居民出行和农村经济社会发展提供了良好的基础。但农村公路中三级或四级公路占比达86%，即低等级农村公路是主体。这类低等级农村公路大部分存在线形指标低、危险路段多、安保设施不完善等问题，且交通事故频发。为保障全国范围内农村公路的安全运行，相继出台了《关于实施公路安全生命防护工程的意见》(国办发[2014]55号)和《公路安全生命防护工程实施技术指南》(试行)(交通运输部发布,2017)，提出要科学组织农村公路隐患路段的安全风险排查，并按照风险程度区分轻重缓急，以进一步规范农村公路安全防护工程的有序实施。由于低等级农村公路里程规模大，安全风险排查工作量大，同时又缺少设计资料和相关数据来源，只能通过现场排查。然而，公路安全风险排查人员提供的农村公路路段安全风险评估信息，通常带有主观性和不确定性。因此，有必要提出一种可以融合主观性和不确定性评估信息的评价方法，以获得相对准确的安全风险评价结果。

针对农村公路的安全风险评价，国内外学者提出了包括事故数据分析、贝叶斯、物元分析、集对分析、熵权法等评价方法。国外学者常采用事故数据分析法研究农村公路的安全风险程度，但该方法不适用于交通事故数据缺乏的地区或国家。在其他评价方法的应用中，大部分考虑由评估专家根据描述的指标条件评定具体的风险指标值，但是主观判断产生的不确定性是无法避免的，即无法处理风险评价中的不确定信息问题。目前提出的评价指标的定量评定方法，具有一定的实际参考意义，但无法应对农村公路现场的综合情况。比如弯道半径指标，在文献[7]中提出了基于弯道半径值和弯道个数的定量评定表，当弯道半径小，且单位里程内弯道数量较多的情况下，即定量为高风险数值，但是如有配套完善的减速、限速，以及急弯、连续弯道等警告标志，其安全风险将显著降低；再比如支路/接入口密度指标，仅以单位里程的支路/接入口数量定量评定安全风险显然也是不合理的，当支路/接入口密度很大时，如在主路上有配套完善的减速、限速，以及交叉口、接入口警示标志和道口标柱，在支路/接入口上有配套完善的减速让行标志等，也能显著降低安全风险。因此，诸如弯道半径、支路/接入口密度等这类指标应该是一种综合型指标，难以进行统一性和唯一性量化，需要结合现场情况进行综合判定。

除此以外，由于人员、时间与经费投入的限制，低等级农村公路路段安全风险评价，不可避免地存在主观性与不确定性问题，需要通过技术方法融合不确定的风险信息，以合理评估风险程度。而证据推理理论的优势就是允许并能接受主观判断产生的不确定性，该理论在船舶航行安全、施工安全、水域运输可靠性等领域均有应用，目前在农村公路安全方面尚无应用。因此，该文构建低等级农村公路路段安全风险评价指标体系，采用COWA算子对评价因素和指标进行赋权，基于证据推理构建低等级农村公路路段安全风险评价模型，对路段安全风险程度进行评价与排序，最后通过案例分析验证该评价模型的适用性与可靠性。

2 低等级农村公路路段安全风险因素与指标

综合考虑引发低等级农村公路交通事故的多种可能因素，结合相关文献[7,15]，确定低等级农村公路路段安全风险因素，包括线形因素、路侧因素、路堤因素、接入口因素。线形因素包括弯道半径、纵坡坡度、弯道视距、线形组合4个指标，其中线形组合是指平面与纵断面线形组合的空间线形，需进行综合判断其是否安全；路侧因素包括离散危险物、连续危险物、净区状况3个指标，其中净区状况是指最右侧车行道以外带状区域内的状况，即是否平坦、有无障碍物等，是否可供失控车辆安全返回行车道，需结合现场情况进行综合评估；路堤因素包括路堤高度、边坡坡度、边坡综合3个指标，其中边坡综合是指除路堤高度与边坡坡度以外，可能影响边坡安全的各类因素的集合，比如低等级农村公路路侧边坡防护等级普遍较低，多为土质边坡，在极端天气情况下极易发生滑坡等情况，该指标需结合现场综合情况进行评估；接入口因素包括支路/接入口密度、支路/接入口视距、支路/接入口角度3个指标。由此，确定低等级农村公路路段安全风险评价的3级指标体系，如图1所示。

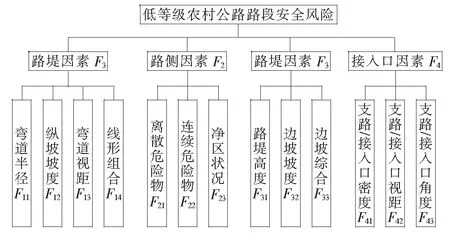
图1 低等级农村公路路段安全风险评价指标体系

在证据推理理论中，对定义指标的评估等级没有具体限制和要求。考虑到各评价指标为综合型指标，即定量与定性相结合的指标。安全风险排查人员需经过统一培训，明确评价指标内涵，以尽量减少由于指标内涵理解差异产生的评价误差。然后，根据现场综合情况和排查人员的经验，依据指标评价集进行评估。借鉴相关文献的安全风险分级情况，采用5级评价集{低风险，较低风险，中等风险，较高风险，高风险}，对应的评估等级为{1,2,3,4,5}。

3 低等级农村公路路段安全风险评价模型

3.1 指标权重确定

为降低不可靠指标信息对赋权结果的影响，采用COWA算子分别对安全风险因素和指标进行相对权重计算，具体步骤如下：

(1)由e个专家评定因素之间的相对重要度，可得因素Fi的决策数据集结数列ci=(ci1,ci2,…,cie)，按照从大到小对数据重新排序，并以1开始编号形成新集结数列di=(di1,di2,…,die)。

(1)

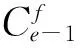
(2)

(3)

3.2 指标评估方法

每个指标由公路安全风险排查人员在分布式评估模型框架下进行评估，分布式评估模型如下：

S(Fi,j)={(Gn,βn,i,j),n=1,2,…,N}，i=1,2,…,K,j=1,2,…,Li

(4)

3.3 证据推理算法

基于分布式评估矩阵Mi中的数据，采用解析证据推理算法计算第i个风险因素的分布式评估结果。分布式评估矩阵Mi中的置信度先要转换为基本可信度mass数，具体公式如下：

mn,i,j=wi,jβn,i,j(n=1,2,…,N,j=1,2,…,Li)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

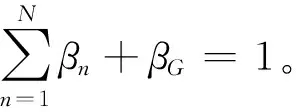
3.4 安全风险排序

假设有M个路段，每个路段的分布式评估为S(Rm)={(Gn,βn(Rm)),n=1,2,…,N}，m=1,2,…,M，其中βn(Rm)为第m个路段评估等级Gn的置信度。该分布式评估提供了路段安全风险的基本信息，但不能直接用于路段安全风险程度的分析和排序。为了比较M个路段的安全风险程度，并确定其优先改造顺序，采用效用函数量化路段安全风险程度的期望值，第m个路段的安全风险期望值为：

(15)

式中：v(Gn)={v(G1),v(G2),…,v(GN)}为评估等级的值集；βn(Rm)为路段Rm的评估等级Gn的置信度下边界，上边界为βn(Rm)+βG(Rm)。

因此，在不完全信息评估中有评估等级Gn的置信度范围。在评估等级集合G中，G1和GN为最低和最高评估等级，分别具有最低和最高值。由此，Rm路段安全风险期望值的最大值、最小值和平均值计算如下：

Emax(Rm)=[βN(Rm)+βG(Rm)]v(GN)+

(16)

Emin(Rm)=[β1(Rm)+βG(Rm)]v(G1)+

(17)

Emean(Rm)=[Emax(Rm)+Emin(Rm)]/2

(18)

若路段所有指标的分布式评估都是完全信息评估，则βG(Rm)=0，E[S(Rm)]=Emax(Rm)=Emin(Rm)=Emean(Rm)。此时，当E[S(Rm)]>E[S(Rl)]时，路段m的安全风险程度大于路段l。若路段中部分指标的分布式评估存在不完全信息评估，则根据安全风险期望值的最大值和最小值对两个路段进行比较。若Emin(Rm)≥Emax(Rl)，则路段m的安全风险程度大于路段l；若Emin(Rm)=Emin(Rl)且Emax(Rm)=Emax(Rl)，则路段m的安全风险程度接近于路段l；其他情况采用以下公式进行比较：

P(Rm>Rl)=

(19)

若P(Rm>Rl)>0.5，则路段m的安全风险程度大于路段l；若P(Rm>Rl)=0.5，则路段m的安全风险程度接近于路段l；若P(Rm>Rl)<0.5，则路段m的安全风险程度小于路段l。

4 案例分析

某三级双车道农村公路，设计速度为40 km/h，全长约3.5 km，选取其中事故高发路段1.6 km(K0+000～K1+600)进行路段安全风险评价。从公路起点处以200 m为单位里程划分为8个路段，分别进行安全风险排查和评价。

4.1 指标权重确定

由5名专家对安全风险因素和指标进行相对重要度评分，评分区间为0～5，以0.5的整数倍进行评分，相对重要度越高评分越高。下文仅以风险因素的相对权重计算为例进行说明，见表1。

表1 安全风险因素相对重要度评分结果

以风险因素F1为例，采用COWA算子计算其相对权重，计算步骤如下：

将F1的重要度评分数值从大到小进行排序，可得d1=(5.0,4.5,4.5,4.5,4.0)。专家人数为e=5，由式(1)计算得加权向量(0.062 5,0.250 0,0.375 0,0.250 0,0.062 5)。再由式(2)计算F1的绝对权重为：

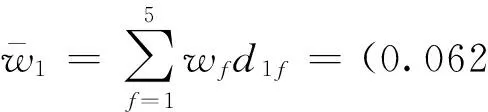
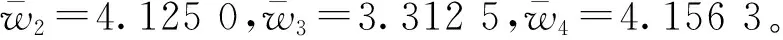
4.2 分布式评估结果

根据安全风险指标评价集和分布式评估模型，由安全风险排查人员对8个路段的每个指标进行分布式评估，其结果见表2。以路段4为例，其中纵坡坡度指标为完全信息评估(70%+30%=100%)；边坡综合指标为不完全信息评估(30%+60%<100%)，由于现场缺少相关信息无法进行完全信息评估；净区状况指标为不完全信息评估，由于该路段近期将进行路侧净区改造，不宜进行评估。

表2 评价指标的安全风险分布式评估结果

由式(5)～(14)计算得8个路段的分布式评估等级结果，见表3。其中路段2、4、7和8由于存在不完全信息评估，产生了置信度βG。分布式评估等级结果反映的是每个路段所属的5个评估等级的概率。以路段5为例，该路段有85.24%的概率在等级1和等级2之间，且显著接近于等级1。

4.3 综合评估结果

根据文献量化评价集的值集v(Gn)={0,0.05,0.15,0.30,0.50}，由式(15)～(18)分别计算8个路段安全风险期望值的最大值、最小值和平均值，其结果见表3。其中路段2、4、7和8存在不完全信息评估，其安全风险期望值的平均值、最大值、最小值有差异，而其他路段均为完全信息评估，三者相等。然后，对8个路段进行对比排序，完全信息评估的路段直接比较Emean的大小，不完全信息评估的路段根据安全风险期望值的最大值和最小值对两个路段进行比较，其他情况根据式(19)进行比较。由式(19)计算得路段相对安全风险矩阵，其结果见表4。其中，路段4、5和8之间，需要根据式(19)的判断条件进行排序。综合表3、4，可得8个路段的安全风险排序，见表5。

表3 路段安全风险分布式评估等级结果与安全风险期望值

表4 路段相对安全风险矩阵

表5 模型评价排序与事故数据排序的对比

4.4 评价效果验证

为验证评价效果，采用评价路段2013年8月至2016年8月期间的交通事故数据进行验证。将事故类型分为财产损失事故、受伤事故、死亡事故3类，采用计分法进行安全风险排序，即3种交通事故类型分别对应取值为1、2、3，由事故次数与对应分值的乘积之和反映基于事故数据的安全风险评分，并进行排序，见表5。采用Spearman等级相关分析法，验证基于证据推理的路段安全风险评价排序与基于事故数据的评价排序之间的相关性。经计算可得：Spearman相关系数为0.952，P-value为0.000，通过了置信度为99%的显著性检验，即模型评价排序与事故数据排序没有显著差异，表明基于证据推理的路段安全风险评价方法可靠性较高。

5 结论

(1)针对低等级农村公路路段安全风险评价中存在的主观性和不确定性问题，基于证据推理理论构建了低等级农村公路路段安全风险评价方法，该方法可融合路段安全风险评价中的完全和不完全信息评估，尤其是当路段中某些指标无法评估时，可根据路段的最大和最小安全风险期望值进行评估，从而实现在不确定信息条件下对低等级农村公路路段安全风险的有效评价。在人员、时间与经费投入有限的情况下，该方法可拓展应用于路段安全风险评估信息存在主观性和不确定性问题的其他类型公路。

(2)以1.6 km三级农村公路(交通事故高发路段)为例，模型评价得出的8个路段安全风险排序与基于事故数据的安全风险排序无显著差异，验证了基于证据推理的路段安全风险评价方法的适用性与可靠性。在公路交通事故数据无法获取的情况下，可相对准确地识别风险路段。

(3)低等级农村公路安全风险评价与排序结果，可为农村公路安全防护工程实施的有序开展提供参考依据，以投入不同程度的安保经费进行交通安全改善，使有限的经费得到合理的安排，达到有序设防，避免盲目设防或过度设防的目的。

(4)该研究重点针对低等级农村公路路段设施条件的安全风险评估，旨在为后续农村公路安全防护工程设计与实施提供依据。因此，评价指标中未考虑路段交通量、平均速度等动态指标，但这些指标是影响路段运行安全风险的重要因素，将在下一步研究中考虑融合这些动态指标，对低等级农村公路路段的运行安全风险进行评估。