“上”形截面双主梁组合梁斜拉桥剪力滞效应研究

于东民

(中交第一公路勘察设计研究院有限公司，陕西 西安 710075)

1 引言

组合梁作为一种优秀结构，广泛应用于大跨斜拉桥、梁桥中。随着经济发展及车辆保有量的增长，斜拉桥也逐渐向多车道、宽桥面方向发展，因此，斜拉桥组合梁的剪力滞效应受到工程界密切关注。

针对组合梁，20世纪70年代，Johnson及Johnson先后采用卡曼理论开展了组合梁有效宽度的分析计算，结果表明组合梁在极限状态下有效宽度约等于翼缘间净距。随后的20年，国外学者利用有限条法、虚拟梁法对大量实桥开展有效宽度相关研究，结果表明：截面尺寸及混凝土板厚度并非主要影响因素，有效宽度主要受到跨径与主梁间距影响；吴文清基于试验数据，开展了简支波折腹板钢-混凝土组合箱梁剪力滞效应的相关研究，明确了影响其剪力滞效应的几何参数，并建立了相应经验公式；Amadio通过进行模型试验，对组合梁弹塑性全阶段的有效宽度开展了分析，并提出负弯矩极限状态下组合梁有效宽度的修正公式；聂建国采用有限元软件对简支组合梁开展了非线性分析，针对塑性阶段有效宽度的主要影响因素进行了参数化分析，给出了组合梁塑性阶段有效宽度简化计算公式；李小珍等依托江津观音岩长江大桥，建立了组合梁空间有限元模型并进行了模型试验，得出组合梁的钢梁与混凝土板交界面在压弯荷载作用下会发生滑移的结论。

考虑到斜拉桥组合梁的实际受力包含轴力，有别于一般组合梁，部分国内外学者针对组合梁斜拉桥的剪力滞效应开展了研究。1999年，Byers对变跨径、变梁宽的工字形双主梁组合梁斜拉桥进行了参数化建模分析，建立了组合梁斜拉桥主梁有效宽度与跨径间的关系，并得出了剪力滞系数修正方法；翟晓亮等通过有限元计算分析了双主梁斜拉桥体系的翼缘板受轴力及弯矩作用下剪力滞系数规律，并建立了该情况下的组合梁翼缘板有效宽度系数实用计算方法；左一泽等对某大跨组合梁斜拉桥开展剪力滞效应研究，并在有限元模型中考虑滑移效应，分析了轴向预应力下桥面板应力分布，并提出了可以考虑轴力非线性传递的有效宽度简化分析手段；程海潜等对轴向荷载下宽肢薄壁双主肋主梁的剪力滞效应开展了研究，推导了能量变分原理下的桥面板正应力计算公式并将计算结果与有限元结果进行了对比，得出轴力作用下双主肋主梁的桥面板应力分布规律；刘泽慧等通过空间实体有限元法，对单箱多室鱼腹形截面箱梁的剪力滞进行了研究。

尽管组合梁包括斜拉桥组合梁的剪力滞效应得到了不同程度的研究，但随着大跨宽桥的推进，以及新截面形式的不断研发与应用，组合梁斜拉桥剪力滞效应仍然需要工程界的关注及研究。基于此，该文通过有限元建模，研究弯压复合作用下“上”形截面组合梁的剪力滞效应及其沿纵桥向变化的规律，研究结果可为相关规范及设计指南提供依据。

2 斜拉桥组合梁剪力滞分析方法

不同于一般组合梁桥，斜拉桥组合梁由于索间距小、相对宽度较大，因此组合梁的钢结构部分是通过钢主梁以及钢横梁、小纵梁形成的格构体系，其上的混凝土板通过不同形式的剪力连接件与钢结构部分形成组合梁整体。

斜拉桥主梁以斜拉索划分，每个节段的内力不同，包括斜拉索提供的轴向力分量，以及恒、活载及斜拉索偏心轴向力形成的弯矩。在这种受力情况及结构体系下，斜拉索在锚固区引入的轴向力，则首先施加给钢主梁部位的混凝土桥面板，其次通过组合梁向桥梁中心线方向传递轴力。此时，沿纵桥向组合梁混凝土桥面板中的应力分布并不均匀，平截面假定已不成立；另一方面，多种荷载耦合形成的弯矩在结构上分布不均，使得弯矩造成的应力沿纵向分布不匀，且形成剪力滞后现象。对于仅由弯矩影响形成的剪力滞效应，通常采用有效宽度系数进行简化表示。而斜拉桥混凝土桥面板受轴向力和弯矩耦合作用，剪力滞分析应考虑这种情况。

对于轴力作用下的组合梁混凝土有效宽度计算，一般忽略活载引起的轴力，直接计算斜拉索拉力的水平力投影。根据文献[9]中提供的算式，可以得到不同拉索形式下的水平力：

(1)

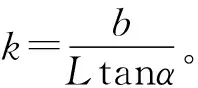
或：

(2)

式中：n为系数，n=k,k+1,…,N-1，其中N为斜拉索总数。

对于弯矩引起的斜拉桥剪力滞效应，既有的分析理论及方法包括卡曼理论、变分原理法、应力函数法以及有限元法。其中卡曼理论、变分原理及应力函数法对于典型截面组合梁如工字钢组合梁等具有一定精度的分析计算能力，但对于异形组合梁的剪力滞分析存在假设不符的情况。相对地，有限元法对于求解任意连续体，可以通过把求解区域进行单元分割，选取节点位移作为未知量并利用弹塑性理论建立单元节点和位移之间的力学关系，最终求解得到模型单元几何体的场函数。

综合考虑上述组合梁剪力滞分析方法，“上”形截面组合梁由于其钢梁与混凝土梁组合部分细节构造特异，与常规工字钢组合梁、钢箱组合梁有区别，传统分析方法无法准确进行计算分析，因此该文采用有限元法进行模拟分析。

3 “上”形组合梁截面特征

双边“上”形组合梁由钢主梁、混凝土桥面板、工字钢钢横梁、工字钢小纵梁组成。其中钢主梁断面还包括腹板纵向加劲肋等构造。

“上”形组合梁截面示意图如图1所示。其中黑色实体部分为钢主梁，其主要部分，即底板、腹板、一侧式顶板形成了“上”形组合梁特有截面形式；混凝土桥面板布置于一侧式顶板上方，通过剪力连接件与一侧式顶板连接；双边主梁通过工字钢横梁、端隔板、中隔板、混凝土桥面板连接形成整体，其中端、中隔板均具有底板以增加刚度；混凝土板下部没有工字钢小纵梁。通过“上”形钢主梁、工字钢小纵梁、工字钢横梁、端隔板及中隔板，组合梁斜拉桥的主梁被分割为格构状，与上方的混凝土桥面板再连接形成完成的“上”形组合梁。

图1 “上”形组合梁截面示意图

4 算例分析

选取某实际工程(双工字钢组合梁斜拉桥)，在有限元分析时替换其主梁为“上”形组合梁。该桥跨径布置为(130+300+130)m，主桥为半漂浮体系，边界条件为索塔处设置竖向支座及横向抗风支座，主梁横向中心间距为34.0 m，混凝土桥面板板厚均为28 cm。斜拉索标准索距为11.5 m，边跨密索区索距为6.0 m。“上”形钢主梁梁高为3 m，混凝土板厚28 cm，主梁截面尺寸如图2所示。斜拉索采用1 670 MPa高强镀锌钢丝，单根拉索可用面积为150 cm2，双塔双索面，全桥共计168根拉索。全桥划分为94个梁段，根据施工阶段类型将这94个梁段划分为主塔区域主梁、一般区域主梁、中跨合龙区域主梁及边跨合龙区域主梁。

图2 算例中“上”形组合梁截面图(单位：cm)

采用Midas/Civil建立全桥模型，得到合理成桥状态下全桥主梁的弯矩内力图及轴力内力图如图3所示，图3(a)可以反映出轴力随着斜拉索增加而在索塔处累积的现象，而由图3(b)可以看出组合梁斜拉桥主梁的弯矩分布与多点刚性支撑连续梁一致的现象。

图3 合理成桥状态下主梁内力图

已知各节段主梁的弯矩及轴力，根据索间距可以将组合梁划分为相应长度的简支组合梁，再基于对应节段的弯矩轴力计算每一个“上”形组合梁混凝土桥面板的有效宽度。

采用Ansys有限元计算平台，对影响“上”形组合梁有效宽度的典型因素开展参数化分析。在有限元模型建立中，采用Shell63单元模拟，混凝土板采用Solid45单元模拟，采用单边悬臂边界条件，通过在拉索锚固截面的节点施加水平分力和竖向分力模拟拉索索力。参数化分析的典型有限元模型节段如图4所示。

图4 有限元模型示意图

(1)弯矩与轴力共同作用下组合梁纵桥向有效宽度系数分布规律

为分析弯矩与轴力共同作用下组合梁纵桥向有效宽度系数分布规律，以Midas/Civil全桥模型内力计算结果为基础，获取其主跨跨中拉索锚固截面的内力，将已获取的内力加载至Ansys有限元模型，得到主跨1/8、1/4、3/8拉索锚固截面的混凝土桥面板上表面应力，如图5所示。

图5 弯压作用下混凝土桥面板上表面应力分布

由图5可知：越靠近主塔根部，混凝土桥面板压应力越大，靠近跨中的截面，由于远离斜拉索锚固端，桥面板中为拉应力，而靠近锚固端的位置轴力作用在“上”形钢主梁上方混凝土板里的效果越明显。并且由于“上”形截面的特殊形式，混凝土板中应力的峰值并不出现在钢主梁的上方，而是出现在腹板正上方的混凝土板边缘上，因此在设计、维护中应考虑这一受力特性带来的施工与管养问题。

(2)宽跨比对“上”形组合梁有效宽度影响分析

为了探究宽跨比对“上”形截面组合梁有效宽度的影响，选取理想有限元模型，研究宽跨比b/L按照0.1间距从0.1变化至1时，受弯“上”形截面组合梁在弹性阶段有效宽度系数变化的规律(图6)。

由图6可得:随着“上”形截面组合梁宽跨比的增大，混凝土板的有效翼缘宽度系数降低，说明随着纵梁腹板中心间距的增大，混凝土桥面板中的剪力滞效应会愈发突出。随着宽跨比的逐步增大，有效宽度系数由0.918减小到0.336，降幅可达63.3%。说明宽跨比对“上”形截面组合梁混凝土板有效宽度系数的影响十分明显，因此在推进大跨、宽桥斜拉桥的设计应用过程中，应当注意增大桥宽对剪力滞效应的负面影响。

图6 弯矩作用下有效宽度系数与宽跨比关系

(3)轴力作用下“上”形组合梁有效宽度分析

选取相同索间距下不同桥宽的有限元模型计算结果并对比分析，从而得到轴力作用下“上”形截面组合梁在弹性阶段有效宽度系数变化的规律(图7)。由图7可知：随着远离斜拉索锚固的梁节段端部，轴力在混凝土板中扩散，从而轴力作用下的组合梁有效宽度，一方面受桥梁宽跨比的影响，另一方面与分析截面所处的纵桥向位置有关。在桥宽由12 m增至16 m再到20 m时，可以看出桥面板有效宽度系数在距离斜拉索锚固端5～15 m距离处区别较大，且桥宽越小，有效宽度系数越大，这一结果与弯矩作用下有效宽度系数分析结果一致。考虑到实际斜拉桥中一个节段主梁的实际长度不会过长，因此分析中距离斜拉索锚固端距离的选取最大为40 m。

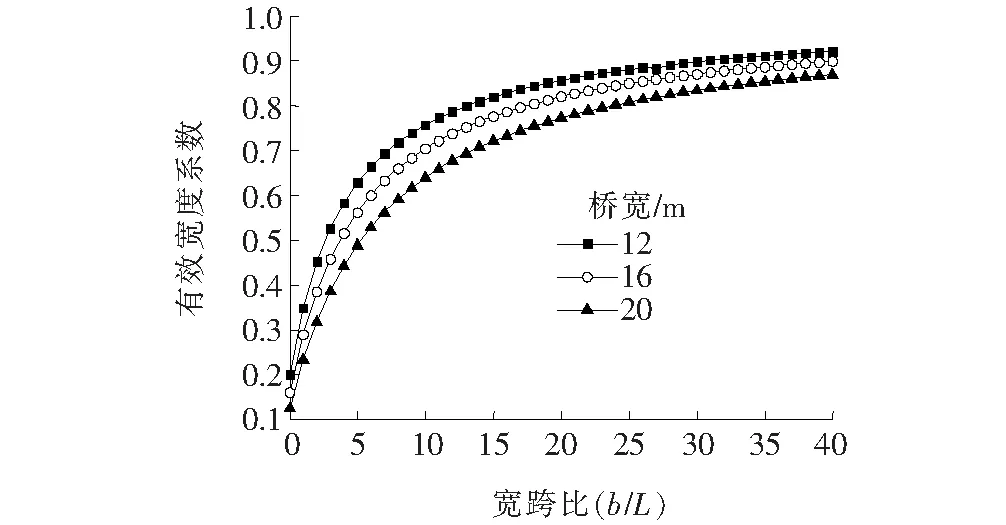
图7 轴力作用下有效宽度系数分析

5 结论

通过对“上”形截面组合梁斜拉桥剪力滞效应影响因素进行模拟计算分析，得到以下结论：

(1)无论是在轴力作用下，还是静载弯矩作用下，对于“上”形截面组合梁斜拉桥，宽跨比是影响其有效宽度的重要因素，宽跨比越大，有效宽度系数越小。

(2)轴力是斜拉桥体系下组合梁的重要内力组成部分，此种情况下，距离组合梁斜拉索锚固端越远，则混凝土桥面板中的有效宽度系数越大，而靠近锚固端的有效宽度系数越小。

(3)受组合梁斜拉桥内力分布特点影响，远离梁端的组合梁混凝土板中的应力分布更加均匀，有效宽度系数更大，而靠近斜拉索锚固端的有效宽度系数更小。