基于改进遗传算法的大体积混凝土温度场预测模型
2021-11-23吕彬李莹炜雷永军王有志张封平
吕彬,李莹炜,雷永军,王有志*,张封平
(1.山东大学 土建与水利学院, 山东 济南 250061;2.山东省公路桥梁建设有限公司)
施工过程中混凝土浇筑量越大,水泥材料水化放热越多,出现温度裂缝的可能性越大。在浇筑前对混凝土内部温度变化规律进行预测对于预防大体积混凝土早期开裂具有重要意义。文献[2]指出由于混凝土热力学参数取值存在一定的偏差导致利用有限元模拟时与实际情况之间误差较大。影响热力学参数的主要因素有混凝土原材料、配合比等,这些因素与混凝土热参数之间呈现出复杂的非线性关系,仅凭经验公式无法对其进行准确取值。随着遗传算法的不断发展,遗传算法开始被广泛地应用于反分析混凝土热力学参数以及温度场预测中。崔溦等利用传统遗传算法反分析绝热温升方程中的3个重要参数实现了对温度场更准确的预测模拟;文献[4]指出传统遗传算法存在收敛速度慢等缺陷。部分学者通过修正算法的选择、交叉和变异方式提高算法性能。孙伟等将模拟退火算法中的Metropolis准则嵌入传统遗传算法的选择操作中对混凝土的热参数进行了反分析;季慧等设计了含有两种交叉算子的新型杂交方式改进了遗传算法。由于遗传算法中的选择和变异方式容易产生较大误差,降低算法的收敛速度和精度,该文将精英策略嵌入选择操作中,动态变异概率、扰动公式和状态接受概率准则嵌入变异操作中,形成改进遗传算法用于热力学参数反分析,对比传统遗传算法的迭代过程可知,改进后的算法计算精度高且收敛速度快。
此外,在针对大体积混凝土温度场的预测研究中,目前对于缺少现场非绝热温升试验数据支撑的预测结果与实际情况间存在较大差距的问题关注较少。因此,该文引入现场非绝热温升试验建立更贴合实际的算法目标函数进行参数反分析,并根据结果建立有限元模型预测某大吨位超宽V形墩在分层浇筑后不同位置处混凝土温度值的变化规律。最后,通过对比施工现场的实测温度值,以验证该文提出的预测模型的准确性。
1 温度场预测原理
温度场预测原理是先根据温度场计算模型确定对预测结果影响较大的热力学参数,再利用改进遗传算法进行参数反分析,最后结合反分析结果建立三维有限元模型得到温度场预测值。
1.1 温度场计算模型
计算温度场时主要包括建立与实际施工条件相对应的热传导微分方程和温度场的边界条件方程两个步骤。其中,热传导方程为:
(1)
式中:T为混凝土测点处温度值;t为混凝土浇筑完成后龄期;a为混凝土导温系数;Q为浇筑过程中由于水泥水化而产生的热量。
浇筑过程中绝热温升可近似为水泥水化热,其计算公式为:
θ(τ)=θ0(1-e-nτ)
(2)
式中:θ0为混凝土最大绝热温升;n为浇筑完成后水化热反应速度。
边界条件方程为:
(3)
式中:Ta为周围环境温度值;T为混凝土测点处温度值;λ为混凝土导热系数;β为混凝土表面放热系数;m为结构物外表面法向。
文献[8,9]中指出:计算浇筑过程中混凝土产热和散热的准确性决定了早龄期温度场预测结果的准确性。由此可判断出,最大绝热温升、水化热反应速度、混凝土导热系数和表面放热系数这4个热力学参数的取值对预测精度影响较大。
1.2 改进遗传算法
传统遗传算法是受生物界进化过程启发后形成的算法,主要包括选择、交叉和变异等过程,该文对传统遗传算法选择和变异方式进行了改进并用于热力学参数反分析。
考虑到包含精英策略的遗传算法能够克服算法局部收敛的缺陷,该文将精英策略嵌入遗传算法的选择中,设计了一种新的方式代替原来的轮盘对赌选择法,具体操作如下:直接复制初始种群中适应度值最高的个体进入子代种群;从其余个体中随机抽取某个体,若该个体适应度值排名位于前30%,以0.8的概率选择该个体;若该个体适应度值排名位于31%~60%,以0.5的概率选择该个体;否则以0.2的概率选择该个体。未被选中的个体则放回初始种群中。嵌入精英策略的选择算子既可减少迭代次数,又可保证种群中的个体都有被选中的可能。
考虑到变异操作极有可能丢失优秀个体,该文对算法中的变异概率和变异方式进行了修正。在进化过程中,变异概率随种群平均适应度的增大而减小。以第一代种群的平均适应度值和最初变异概率为基础,适应度值每增大50%,变异概率降低10%。同时,用扰动公式代替变异算子进行变异操作,并依据状态接受概率准则判断是否接受扰动后个体进入子代种群。改进后的变异方式既能够保留优秀个体,又能够提高种群多样性。扰动公式为:
(4)
(5)
Tk=T0∂k
(6)
式中:mi为未扰动值;m′i为扰动后值;sign为符号函数;u为[0,1]上均匀分布的随机数;Tk为系统温度值;∂为衰减因子;k为进化代数。
状态接受概率准则通过比较扰动前个体和扰动后个体适应度值判断是否接收扰动后个体进入子代种群。若扰动后个体适应度值较高,则接受扰动后个体进入种群;若扰动后个体适应度值较低,则根据式(7)计算其被种群接受的概率p,若p小于[0,1]之间的随机数,则接受扰动后个体;反之,保留扰动前个体。
(7)
式中:fi为扰动前后个体目标函数差值。
2 温度场预测模型
温度场预测过程为:先根据施工方案设计非绝热温升试验;再依据试验的实测温度建立改进遗传算法的目标函数进行混凝土热力学参数反分析;最后将得到的热力学参数值输入有限元模型得到预测值。
2.1 非绝热温升试验
2.1.1 非绝热温升试验方案
某大吨位超宽V形墩为倒梯形截面,分层浇筑,一次浇筑的垂直高度为2 m,宽度为2 m,长度为14.26 m。由于V形墩的斜腿较长,设计试验试块时在其长度方向上截取2 m模拟浇筑过程,试块的其余几何尺寸与V形墩实际情况保持一致,故非绝热温升试验选用2 m×2 m×2 m的C50混凝土立方体块浇筑于0.3 m厚的C30混凝土垫层上的试验方案。在试块两个对立侧面布置100 mm厚的聚苯板保温层模拟V形墩混凝土沿长度方向上的热交换情况。在立方体试块内埋入温度传感器(具体位置如图1、2所示)记录不同位置处混凝土浇筑完成后各龄期温度值的变化情况。
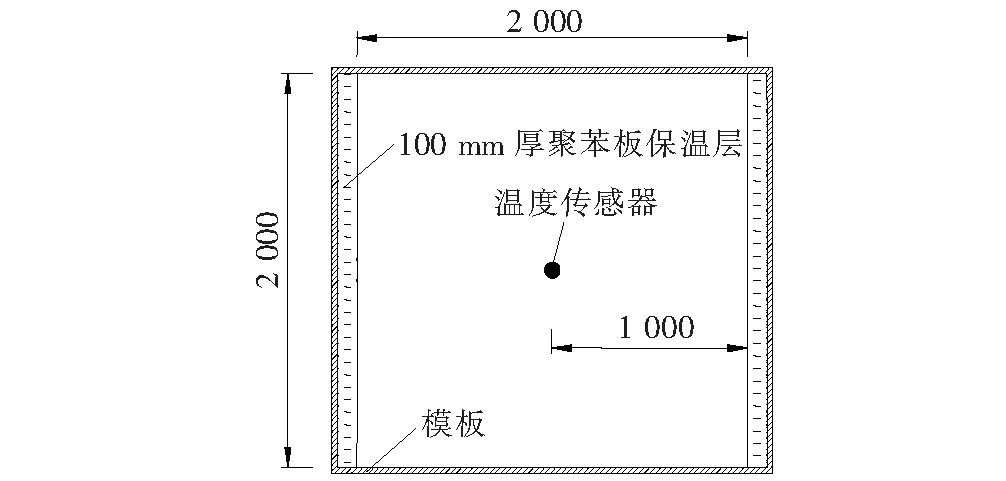
图1 温度传感器平面布置图(单位:mm)
试验的立方体块的浇筑和养护方式与V形墩一致:浇筑5 d后拆模,洒水保湿,0.02 m厚的保温层保温,保证养护温度为10~50 ℃,养护时间为7 d。
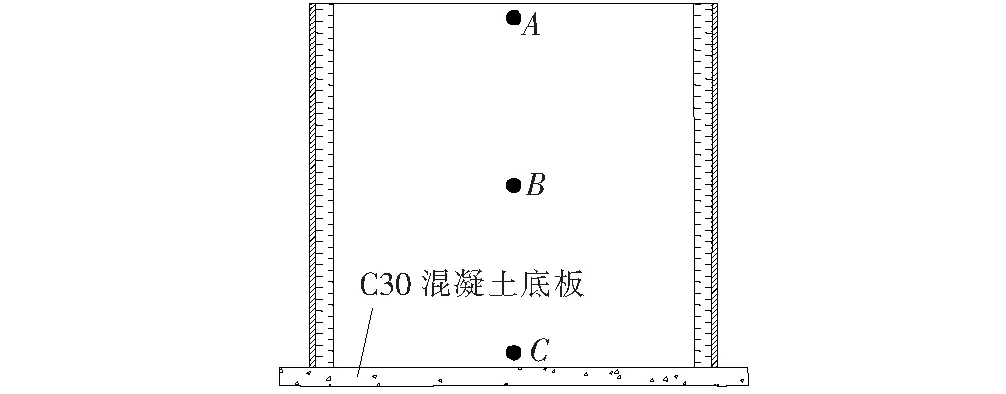
图2 温度传感器立面布置图
2.1.2 非绝热温升试验结果
非绝热温升试验中在A、B、C各点的长、宽、高3方向上各埋入2个温度传感器,共计18个。浇筑完成后不同位置处混凝土各龄期平均温度值见表1。使用温度采集仪记录浇筑完成后各时间段内大气温度值。
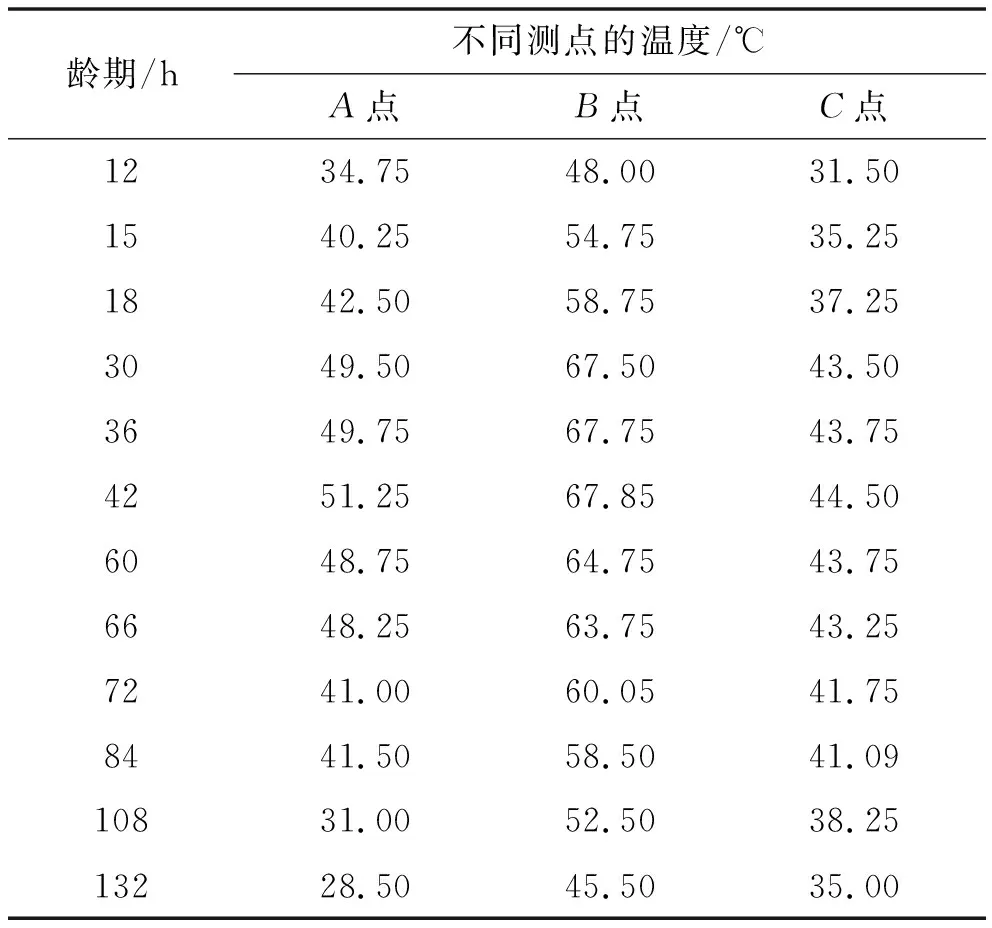
表1 不同测点混凝土温度平均值
2.1.3 非绝热温升试验模型
由于试验试块具有对称性,建立1/4体积的立方体试块的计算模型,如图3所示。为充分考虑C30混凝土垫层对立方体试块传热和散热的影响,垫层尺寸设置为0.3 m×2 m×2 m,并选用固定支座约束作为边界条件。由于聚苯板保温层仅影响C50混凝土与空气之间的热交换率,故只需设定对流系数。根据文献[12]得,C50混凝土与聚苯保温板的对流系数为0.025 kJ/(m2·h·℃);与保温层的对流系数为19.16 kJ/(m2·h·℃)。
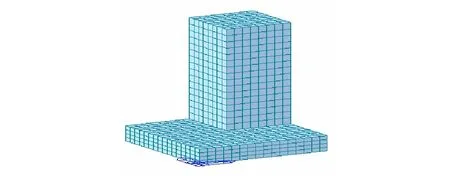
图3 1/4体积立方体块有限元模型
2.2 热力学参数反分析
设定改进遗传算法的各系统参数取值如下:种群中个体数N为30,初始温度值T为500 ℃,温度衰减因子∂为0.8,个体多点交叉概率pc为0.75,个体最初变异概率pm为0.3。热力学参数范围如表2所示。具体流程如图4所示。

表2 C50混凝土热力学参数范围
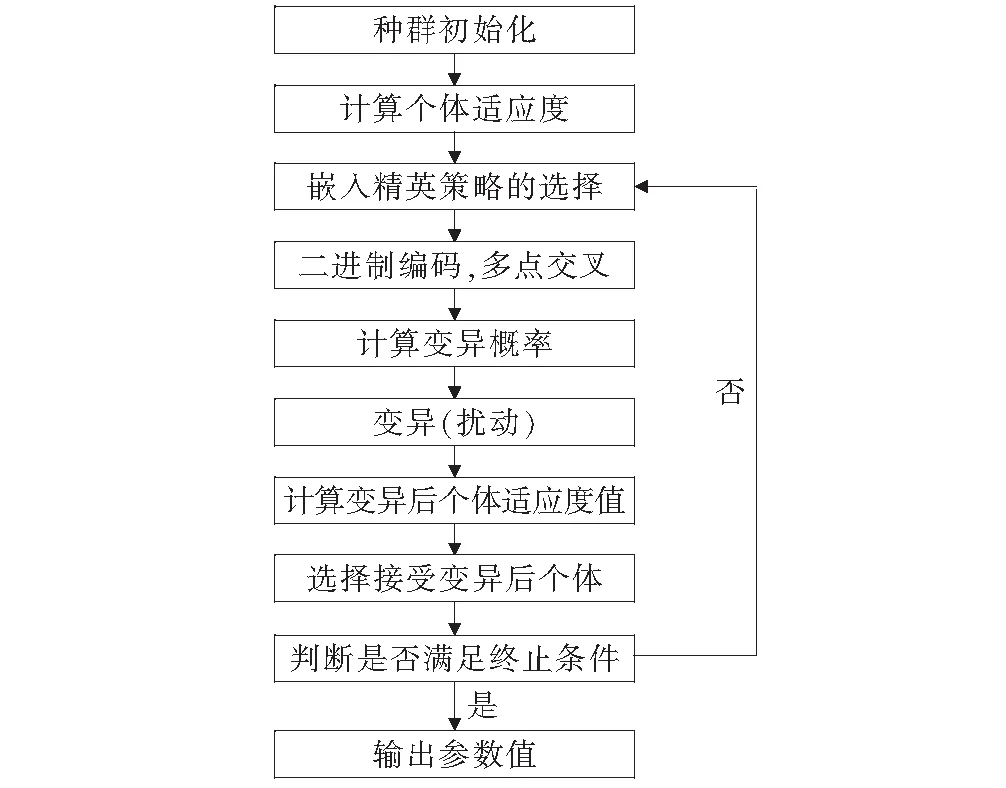
图4 反分析流程图
(1)种群初始化。从各参数取值范围中随机抽取30组参数值作为初始种群。
(2)计算个体适应度。先通过非绝热温升试验有限元模型得到计算值,再通过式(8)、(9)计算个体目标函数值和适应度值。
(8)
(9)
式中:T为模型计算值;Tm为非绝热温升试验实测值;Φ为该个体目标函数值;f为该个体适应度值。种群中个体的适应度值越高,与实测值间误差越低。
(3)选择。依据计算得到的种群中个体适应度值,对初始种群进行嵌入精英策略的选择操作形成父代种群。
(4)编码。所有参数进行二进制编码。
(5)交叉。将父代种群中个体两两随机配对后,依据系统设定的个体多点交叉概率进行多点交叉操作,形成子代种群。
(6)变异。计算本代的变异概率,利用扰动公式进行变异操作,计算变异后个体适应度值后,依据状态接受概率准则判断是否接收变异后个体进入子代种群。
(7)终止。当连续多代子代种群中全部个体的平均适应度值间的差异小于设定值时,程序终止。若程序终止,将子代种群中的最佳个体作为最终结果输出;否则将子代种群作为初始种群继续迭代。
2.3 V形墩有限元模型
结合算法参数反分析的最终结果和现场施工方案建立V形墩模型如图5所示,底部选用固定支座作为约束条件,现场采集的大气温度值作为环境温度函数。

图5 V形墩有限元模型
3 温度场预测结果对比
3.1 收敛速度对比
为更好对比改进后算法的性能,同时编写改进遗传算法和传统遗传算法程序并从随机抽取的同一组初始种群开始进化。两种不同算法在参数反分析过程中每次种群进化时最佳个体适应度值如图6所示。
由图6可知:改进遗传算法经过13次迭代后程序终止,得到适应度值为0.041的最佳个体;传统遗传算法经过28次迭代后程序终止,得到适应度值为0.022的最佳个体。改进遗传算法可以在提高最佳个体的适应度值的同时明显减少种群进化次数,高效地进行混凝土热力学参数反分析。
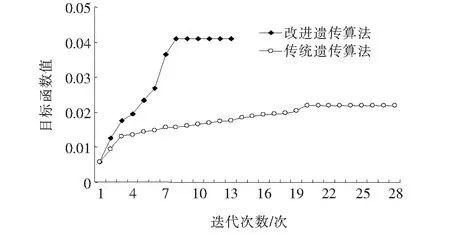
图6 不同算法反分析过程对比
3.2 反分析参数精度对比
为进一步对比两种算法参数反分析的计算精度,通过现场试验计算得到热力学参数实测值,与两种算法反分析值对比如表3所示。由表3可知:相较于传统遗传算法,改进后的算法反分析得到的结果更贴近实测值,具有更高的精度。
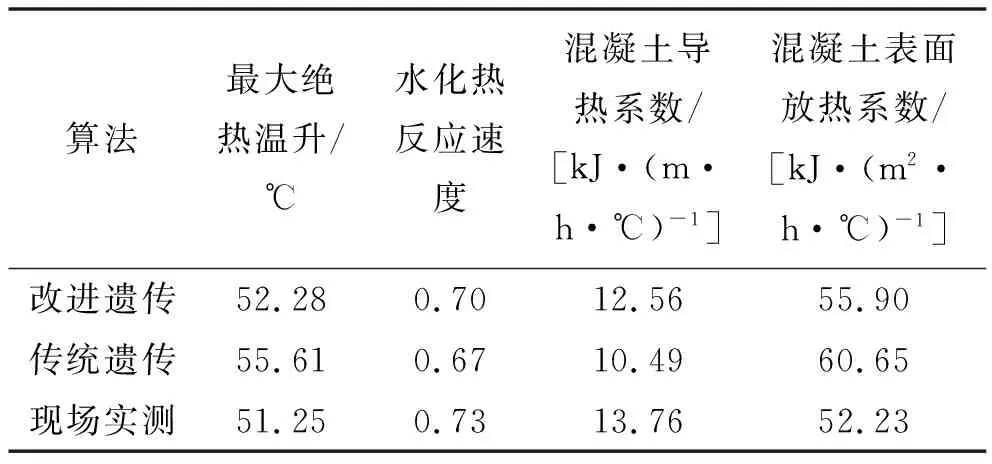
表3 不同算法反分析结果与现场实测对比
3.3 预测精度对比
在V形墩内部埋入温度传感器记录不同位置处混凝土浇筑完成后各龄期温度值的具体变化情况。V形墩上部和下部混凝土各龄期温度场基于改进遗传算法和传统遗传算法的预测值以及现场实测值如图7、8所示。
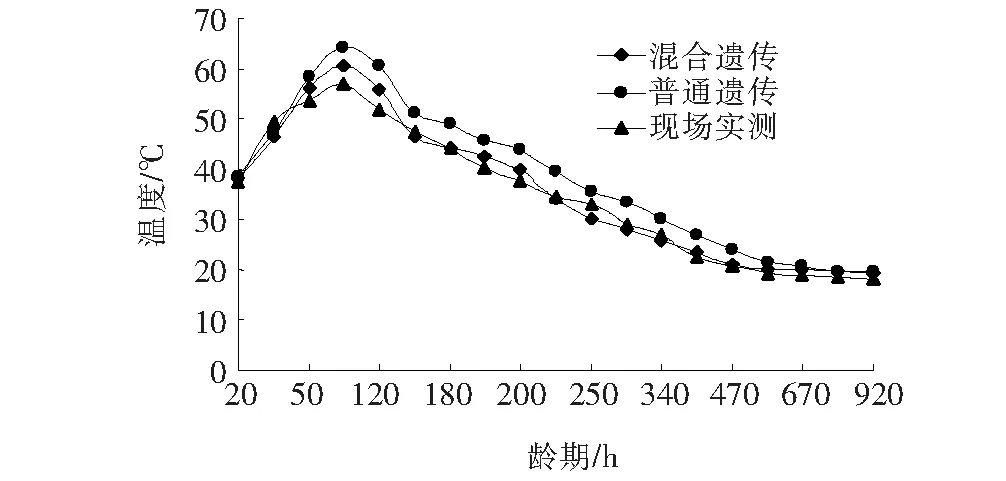
图7 V形墩下部混凝土各龄期温度值
由施工现场实测温度和模型预测值可知,不同位置处混凝土在浇筑完成后均呈先迅速升温再缓慢降温的变化规律。混凝土浇筑完成80~90 h后V形墩混凝土温度升至最高,800~840 h后温度降至大气温度附近。为更好对比预测精度,计算基于两种不同算法的各龄期温度场预测结果的相对误差如表4、5所示。
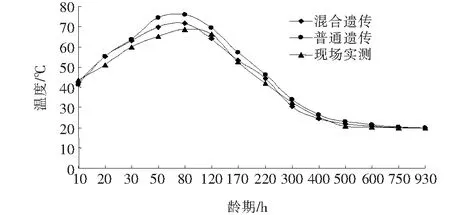
图8 V形墩上部混凝土各龄期温度值
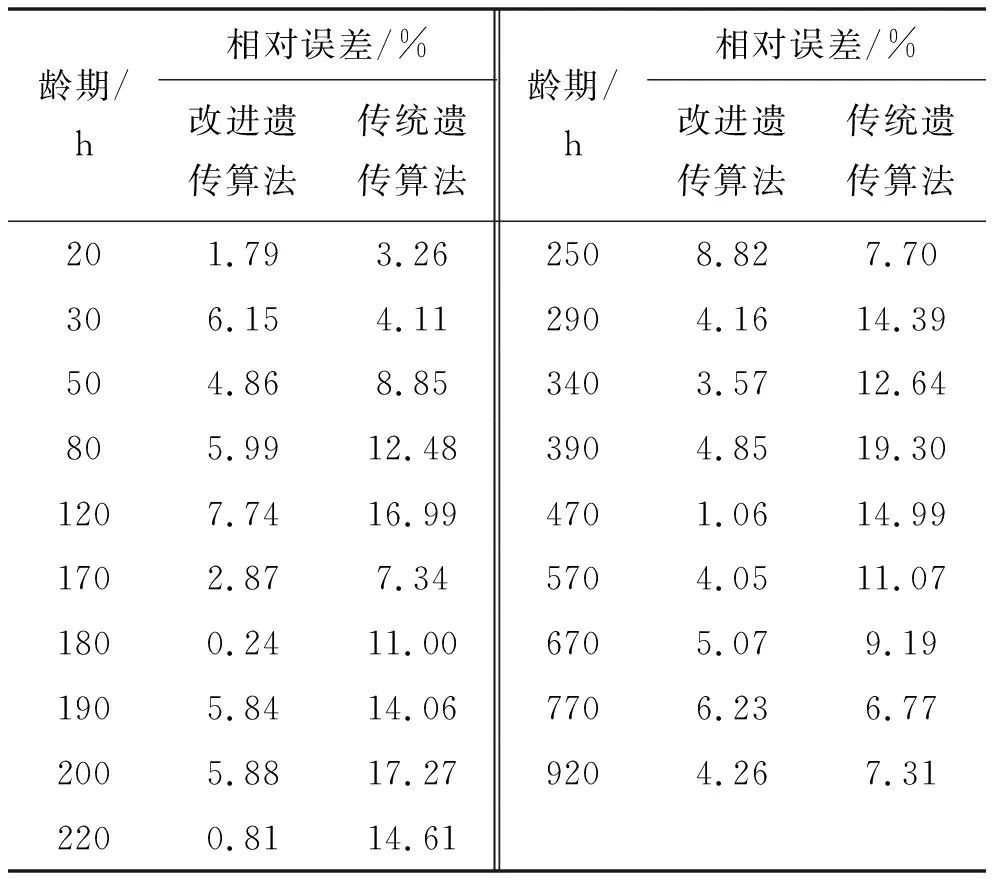
表4 下部混凝土温度值相对误差

表5 上部混凝土温度值相对误差
由表4、5知:相比基于传统遗传算法的预测模型,基于改进遗传算法的预测精度更高,可以很好地反映施工现场的温度变化情况。
4 结论
(1)将精英策略、动态变异概率、扰动公式和状态接受概率准则嵌入遗传算法,引入非绝热温升实测温度建立目标函数,提出了改进遗传算法,利用此算法反分析出的热力学参数建立有限元模型预测了某大吨位超宽V形墩浇筑初期不同位置处混凝土温度值,并利用现场实测温度验证了该文提出模型的预测精度。
(2)通过对比基于改进遗传算法的预测结果与传统遗传算法预测结果验证了该文提出的改进遗传算法可在明显提高预测精度的同时减少种群进化次数。
(3)虽然以某大吨位超宽V形墩为例,但其他涉及大体积混凝土工程的温度场预测过程具有相似性,施工时可利用该文模型进行预测,可为合理布置及调整温控措施提供理论依据。
