基于Hough变换的3D-HEVC深度图快速帧内预测方法
2021-11-23钟国韵杨德明何月顺刘梅锋
钟国韵, 杨德明, 何月顺, 张 军, 刘梅锋
(东华理工大学 信息工程学院,江西 南昌 330013)
随着3D视频技术的发展,人们发现3D视频带来比二维视频更逼真的视觉效果。但是3D视频数据量是巨大的,尤其是高清甚至超高清3D视频,其存储和网络传输是个巨大的负担。为了解决其数据量大的问题,视频编码专家组(VCEG)和活动图像专家组(MPEG)组成联合视频组(JVT),在高效视频编码(HEVC)第三版本中加入了3D-HEVC标准(Sullivan et al.,2012)。该标准编码的3D视频是由多视点视频(MVD)加上深度图组成(Merkle et al.,2007),该标准本身由H.264(Wiegand et al.,2003)同一标准中多视点视频编码(MVC)技术发展而来(Sarker,2014;Vetro et al.,2011)。得益于该标准的制定,3D视频才能更高效地进行存储和网络传输。
3D-HEVC增加了深度建模模式(DMM),目前DMM包括DMM1模式和DMM4模式(Muller et al.,2013),而DMM模式带来了巨大的计算复杂度。与HEVC方面研究人员提出的众多快速压缩编码方法(钟国韵等,2013;刘梅锋等,2014)类似,许多专家学者投入到降低计算复杂度方面的研究,也提出了较多有效方法。3D-HEVC快速视频帧内编码方法主要包括跳过DMM模式和模式判决两种,前者利用边缘分类(Park,2015)、空间相关性(Zhang et al.,2015)、四叉树(Zhang et al.,2014)、编码单元(CU)纹理(Chen et al.,2019)、边缘检测(李强等,2020)等各种信息来跳过DMM模式;后者通过计算残差(Zhang et al.,2016)、模重因子(Shen et al.,2018)、深度灰度相似性(Lei et al.,2018)、方差平方欧式距离(Zhang et al.,2018)、多视点合成(Dou et al.,2017)、蛙跳算法(Jaballah et al.,2016)等方式来进行模式判决。
尽管现已报道的方法能较好地降低3D视频深度图编码计算的复杂度,但是对于DMM模式的角度选择,仍没有较准确的判决。拟采用直线检测的方法,一方面可以依据它跳过DMM模式的遍历,另一方面,可根据直线的角度,粗略选择少数几种角度的DMM1模式,从而可跳过大部分模式计算过程,以此来实现大幅降低计算复杂度的目标。
1 Hough变换原理
Hough变换为一种图像特征提取技术,可用于检测图像中不同长度的直线,它利用两个不同坐标系之间的变换将一个坐标上相同形状的直线映射到另一个坐标的一个点上形成峰值,通过设定峰值高度阈值判断第一个坐标上的直线。众所周知,一条直线可以在两种坐标上进行表示:①在笛卡尔坐标系上,可以用斜率和截距表示;②在极坐标系上,可用极径和极角(r,θ)表示,如图1所示。
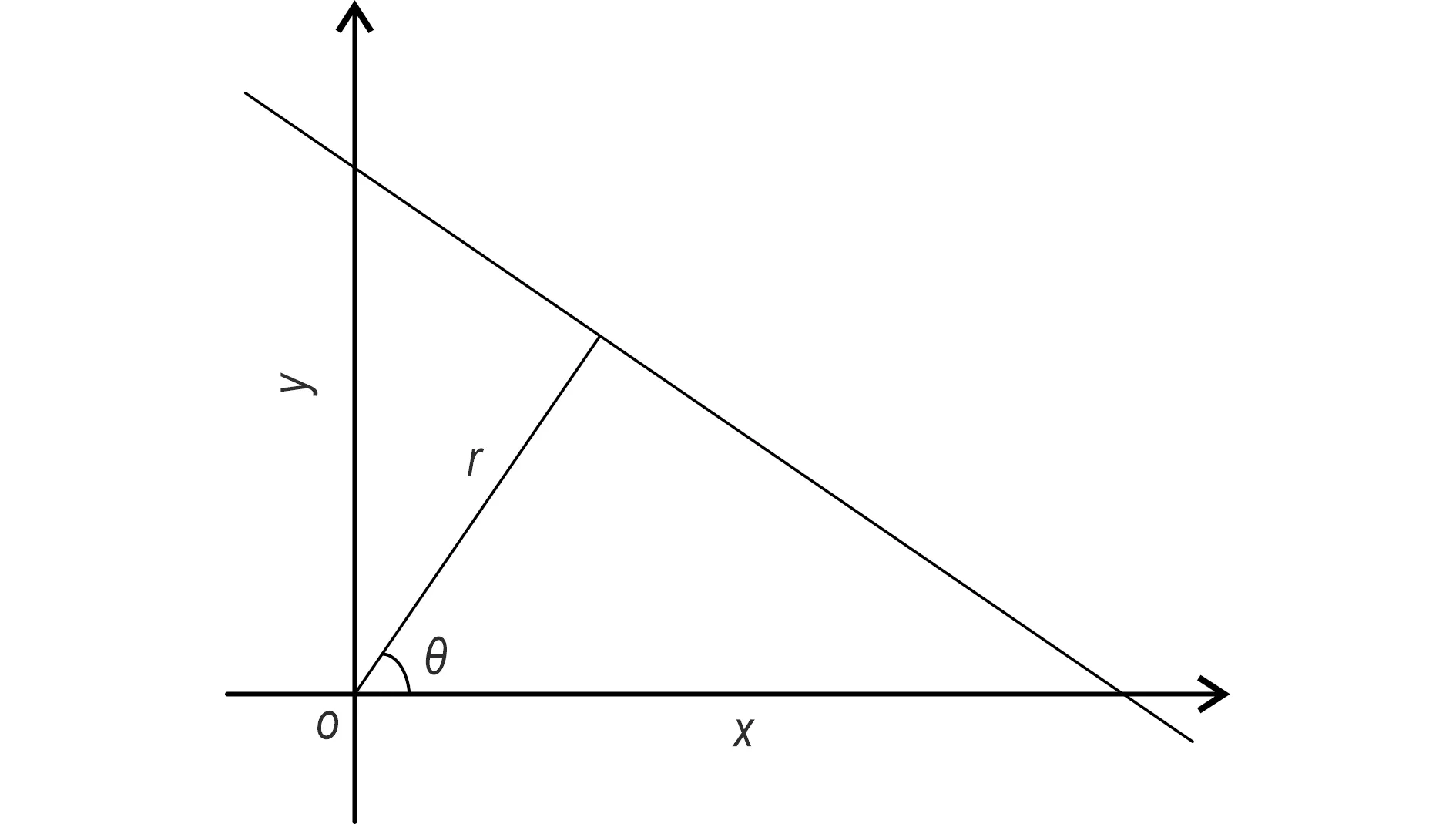
图1 Hough 变换两种坐标对应关系Fig.1 Relationship between two coordinates for Hough transformation
因此,对于Hough变换,可以采用另一种极坐标来表示:
(1)
上式经过化简则可得到:
r=xcosθ+ysinθ
(2)
从以上式子可以看出,笛卡尔坐标中的一个点,映射到极坐标上是一条曲线,因此,多个点连成的一条直线,可以通过在r-θ坐标系上寻找交于一点的曲线数量来检测,越多的曲线交于这点就意味着在这条直线上有越多的点。于是,可以通过设置直线上点的数量阈值来定义多少条曲线交于一点才算检测到一条直线。
2 基于Hough变换的快速3D-HEVC深度图帧内预测方法
2.1 深度图帧内预测计算复杂度分析
3D-HEVC中深度图的帧内预测编码共有37种模式,其中35种模式是继承了HEVC帧内预测模式,模式0为Plannar模式,模式1为DC模式,模式2至34为Angular模式(Sanchez et al.,2016)。除了HEVC的35种模式,另外还有两种DMM模式,分别为DMM1模式和DMM4模式,如图2所示。阴影部分与白色部分像素分别用各自区域内常量代替区域内所有像素值。DMM1模式的分割线方式如图2c所示,其分割角度数量巨大,其中4×4到32×32尺寸分辨率,分割角度数量分别为86、782、1 392和1 503,即每种角度下均需进行编码,其计算量非常大。
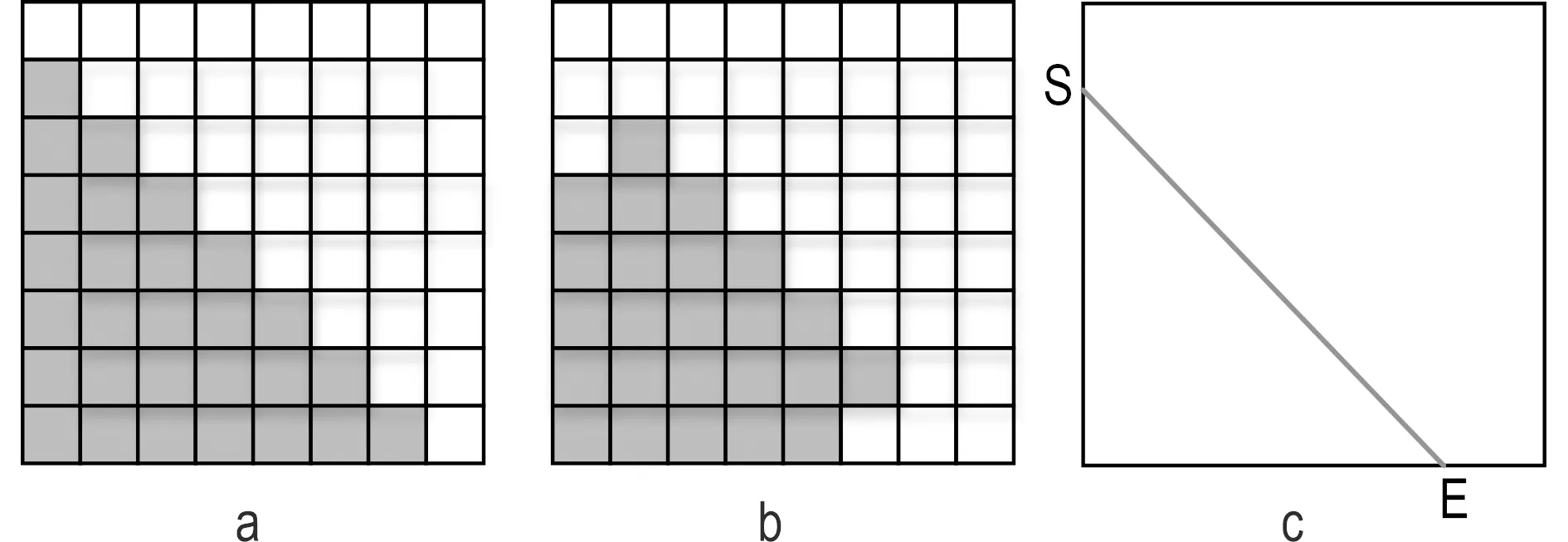
图2 DMM模式示意图Fig.2 DMM diagrama.DMM1模式;b.DMM4模式;c.DMM1分割线
2.2 基于Hough变换的3D-HEVC视频序列中深度图边缘直线检测
深度图的特点是边缘相比纹理图要光滑得多,从细节处观察,大部分边缘均为直线或接近直线。另外, 3D-HEVC深度图的帧内预测编码模式中,由于DMM1模式计算复杂度较大,其分割模式采用直线。因此,采用Hough变换来检测3D-HEVC视频序列中深度图边缘直线,如图3为测试序列Undo Dancer中一帧深度图经过Hough变换后检测到的直线段。从图3中可以看出,深度图中几乎所有的直线边缘部分均被检测出来,在正常的3D-HEVC深度图的帧内预测模式选择中,这些直线边缘部分的预测单元(PU)分块会在DMM1模式选择过程中用直线分割为两部分。

图3 测试序列Undo Dancer深度图中一帧图片经Hough变换检测到直线段Fig.3 Line checked by Hough transformation in one frame of the depth sequence of the test sequence Undo Dancer
2.3 基于Hough变换检测直线的DMM模式跳过判决
3D-HEVC中,深度图中DMM模式包括DMM1模式和DMM4模式,通过Canny边缘检测来判决DMM模式的跳过,对于不能跳过的DMM模式,进一步通过Hough变换来跳过DMM1模式。
2.3.1 利用边缘检测跳过DMM模式
Canny边缘检测分别采用水平和垂直两个模板对图像进行卷积来求某像素点的水平和垂直梯度,其中模板Gx和Gy为:
(3)
总的梯度幅值为:
(4)
为了方便计算,取其近似值:
G=|Gx|+|Gy|
(5)
OPENCV库中的Canny算子中有2个阈值T1和T2,当幅值G超过阈值T2时,判决为边缘;当小于T1时,则排除该像素;当幅值介于两者之间时,若该像素与高于阈值T2幅值相邻,则判决为边缘像素。以上规则符合算法的需求,因此,当PU分块内无边缘像素时,则可跳过DMM模式的计算遍历。
2.3.2 利用Hough变换检测直线跳过DMM1模式
在3D-HEVC中深度图帧内预测的DMM1模式中,笔者采用Hough变换在深度图中检测直线,用该直线把PU分块分割成两部分,并以此为依据对当前PU分块进行DMM1模式的判决,因此,需要从直线在PU分块内部所处的位置来分析。
对于当前PU分块,只有当一条直线穿过它,在PU分块中间没产生任何折线时,才能对应DMM1模式。如图4所示,直线的首尾点分别为A和B,其中线段CD在PU分块之内。
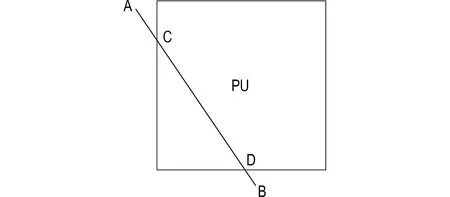
图4 直线穿过PU分块情况Fig.4 Situation where the PU is passed through by one line
若出现如图5所示情况,则可跳过DMM1模式的计算遍历。图5a中PU分块内无直线穿过,因此可以跳过DMM1模式的计算遍历,大部分区域均为该情况,因此可以较大程度降低计算复杂度。图5b中PU分块内有直线,但是直线段的首尾均在分块内部,这种情况下,也不满足DMM1的条件。图5c也不满足条件。
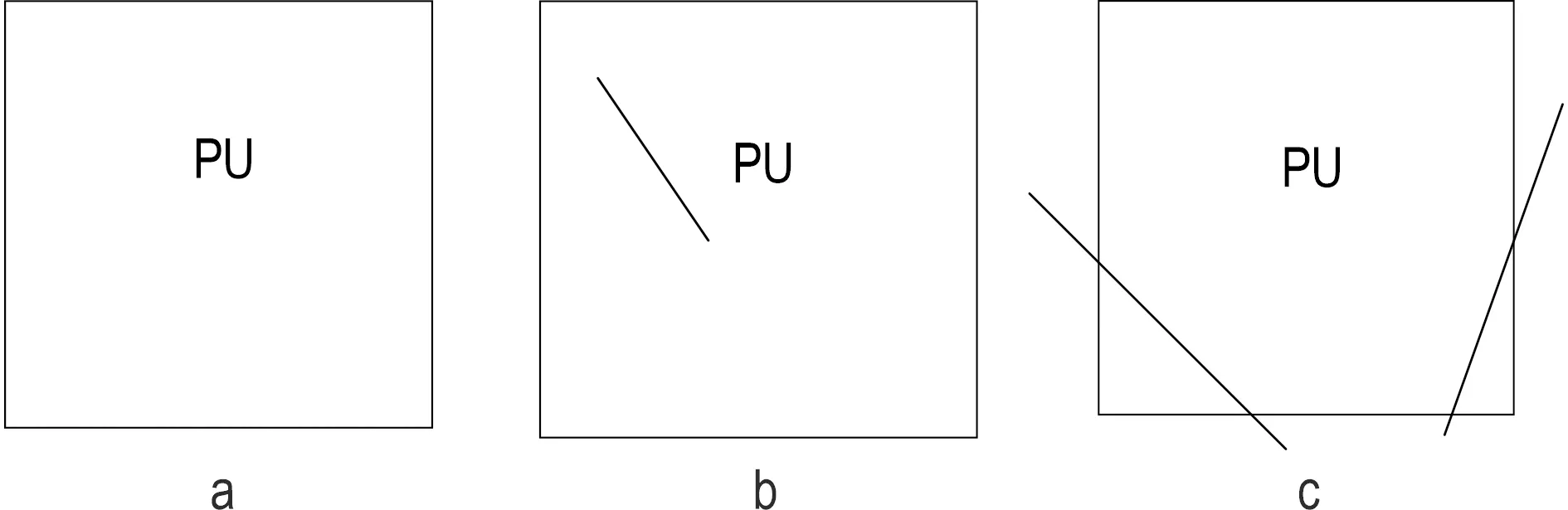
图5 各种可跳过DMM1模式的情况Fig.5 Various situations that the DMM1 mode can be skippeda.PU分块内无直线;b.PU分块内部有1条直线;c.PU分块有2条以上直线穿过
对于如图6所示的CU分块,其模式选择流程如下:
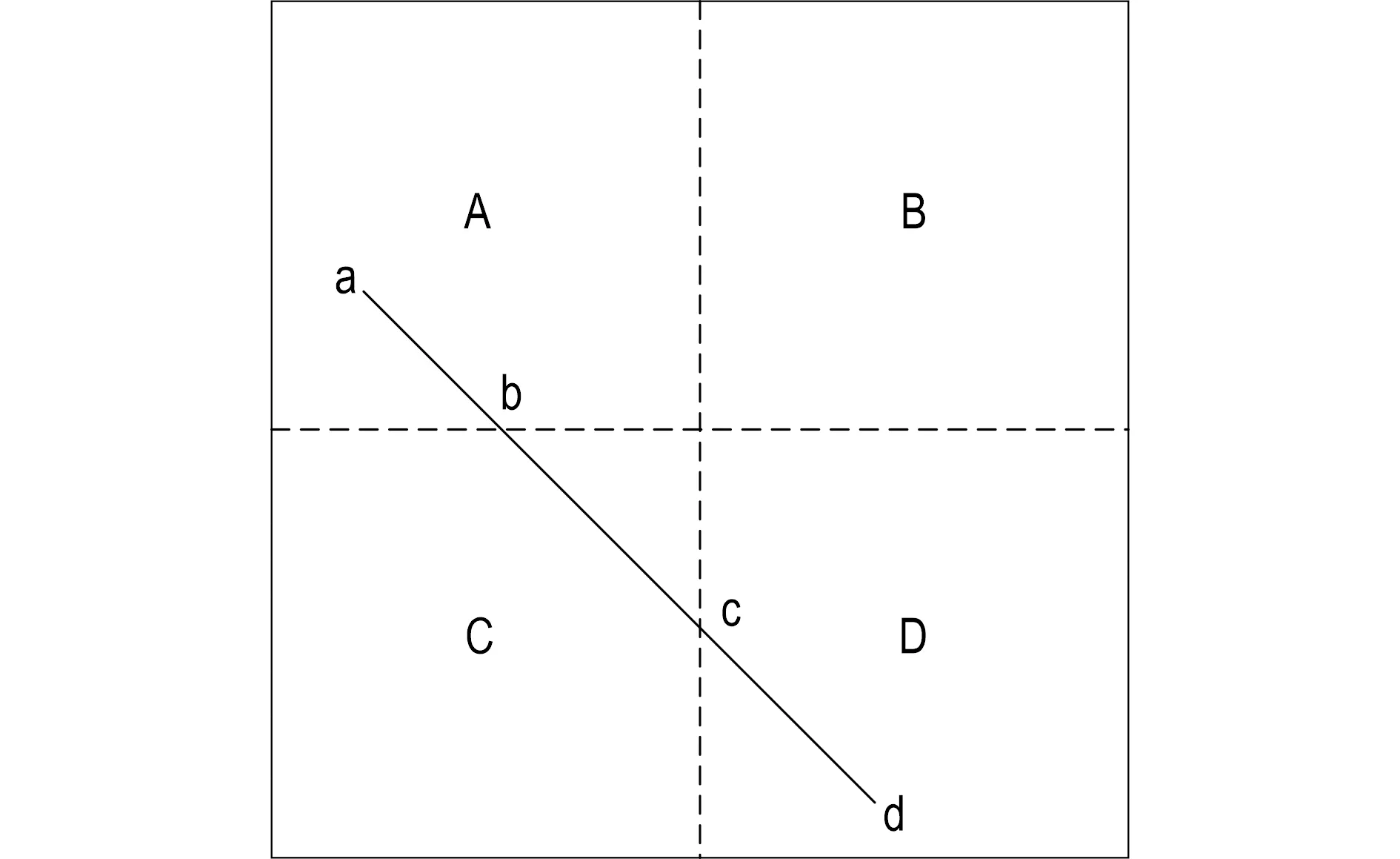
图6 CU分块分级情况下DMM1模式跳过判决Fig.6 DMM1 mode skipping decision under CU block dividing
(1) 当内部有直线段ad,当前CU分块的PU分块可以跳过DMM1模式的计算遍历。
(2) 把当前CU分为A、B、C和D等4个相同的CU分块。
(3) 当进行对应的PU分块模式选择时,其中:①分块A由于内部有线段ab,端点a在PU分块内部,因此A可以跳过DMM1模式计算遍历。②分块B由于内部无直线,也可以跳过。③分块C只有一条直线穿过,因此,分块C需要进行DMM1模式的计算遍历。④与分块A情况类似,分块D也可以跳过DMM1模式的计算遍历。
2.4 直线分割角度判决
为了便于分析,将每个PU分块的最外围一圈像素标上序号,如图7所示,以8×8尺寸的PU分块为例,共有28个点。当一条直线穿过当前PU分块时,可利用Hough变换检测到该直线,设该直线与PU分块相交于点3和点12,考虑到Hough变换中可能存在的误差,除了直线(3,12),即点3与点12相连的直线,需另外计算遍历另4条直线的模式:直线(4,11),(4,13),(2,11)和(2,13),如图7中各条虚线所示。若推广到各种尺寸的PU分块,设Hough变换检测到深度图内的直线穿过PU分块直线为(i,j),则在DMM1模式角度计算遍历过程中,除了直线(i,j),还需另外计算遍历4条直线:直线(i-1,j-1),(i+1,j+1),(i-1,j+1)和(i+1,j-1),从而跳过其他大量角度的计算遍历,大幅降低计算复杂度。
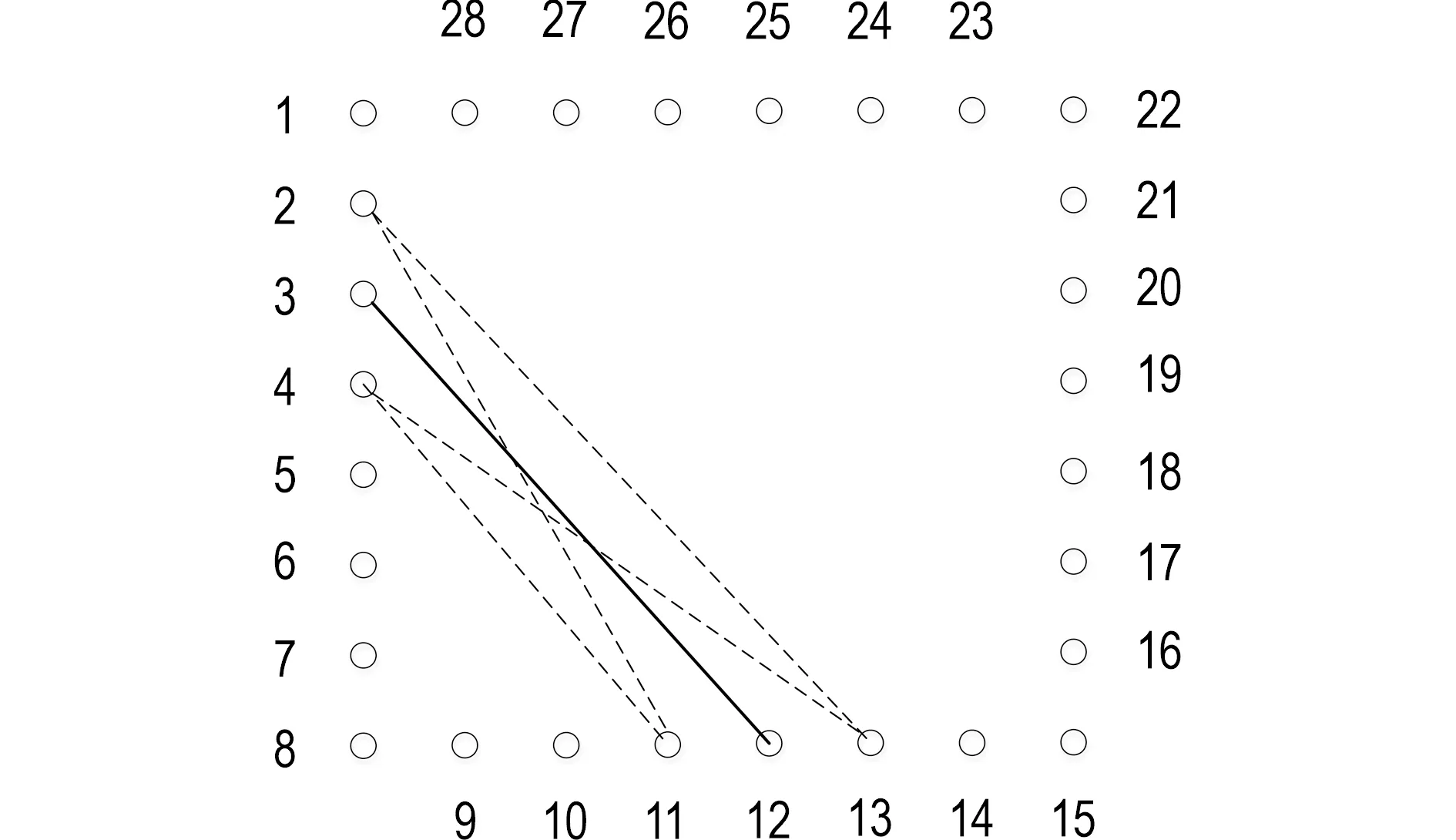
图7 PU分块内直线计算遍历角度Fig.7 Line angles computed in PU block
2.5 整体流程
总体流程如图8所示。对于当前深度图的DMM模式选择,先对该图进行边缘检测,获得深度图的边缘信息二值图。然后对二值图进行Hough变换,检测到深度图中边缘的直线段信息并保存。在当前CU分块PU的DMM模式选择过程中,先判断当前PU分块中是否有边缘,若否,则跳过DMM模式(包括DMM1和DMM4模式)的遍历;若有,则判断当前PU分块中是否只有1条直线穿过,若是,则根据穿过直线的角度和位置,进一步计算遍历与该直线角度接近的4条直线的DMM1编码模式,把率失真代价最小的模式加入到候选模式中;若否,则跳过DMM1模式选择。最后判决当前CU分块尺寸是否为8×8,若是,则结束;若否,则把当前CU继续划分为4个相同的CU,每个CU继续进行上述步骤。
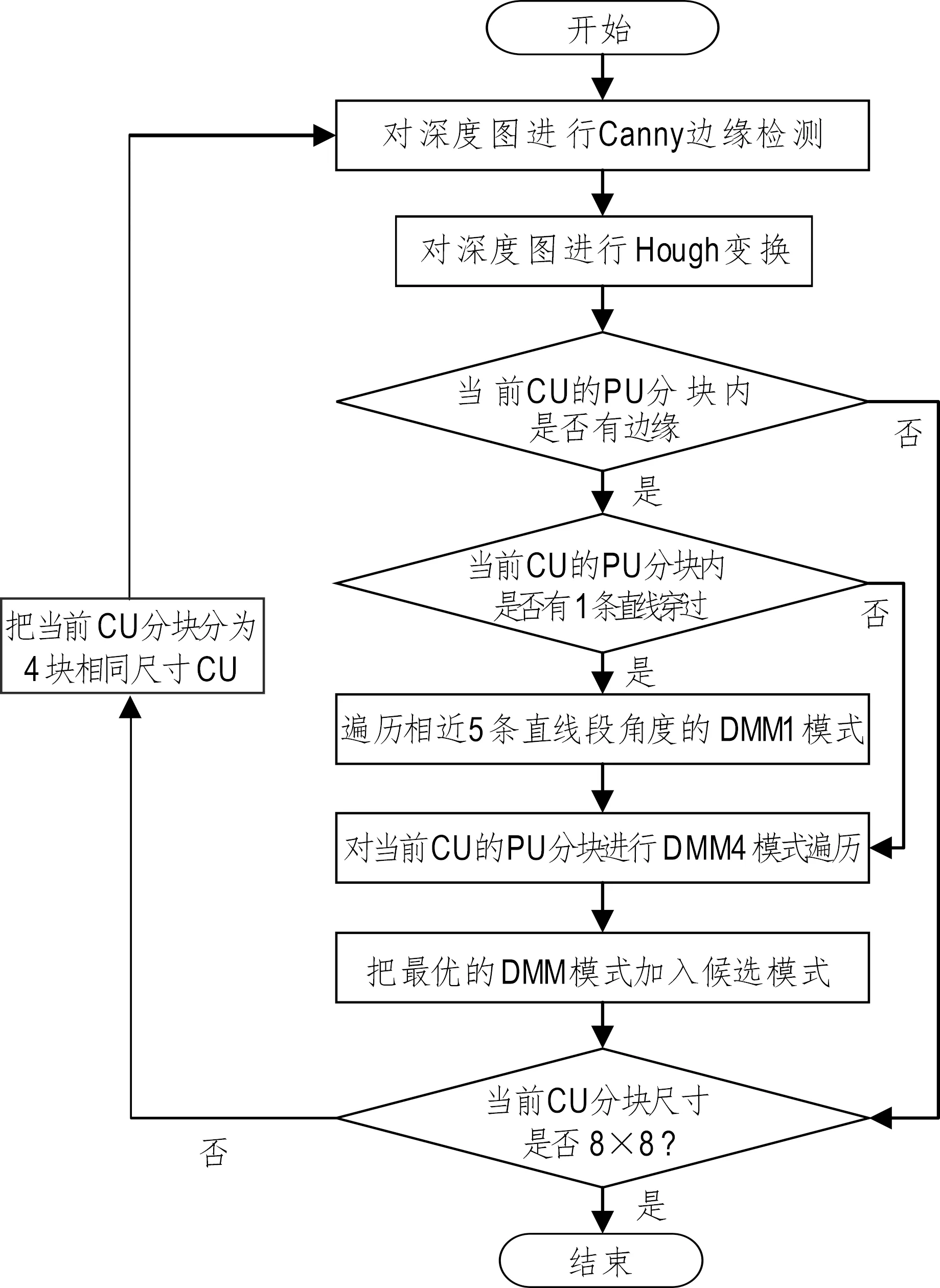
图8 总体流程图Fig.8 Whole flow chart of the proposed method
3 实验结果及分析
采用3D-HEVC的标准测试软件HTM16.2对该方法进行性能测试。测试硬件配置如下:CPU为i7 9700,主频为4.7 GHz,内存为64 G,WINDOWS 64位系统,测试序列为Balloons、Kendo、Nespaper_CC、GT_Fly、Poznan_Hall2、Poznan_Street、Undo_Dancer和Shark等8个标准序列(Mueller et al.,2014),由于研究的是帧内预测方法,故采用全帧内预测编码的模式,量化步长方面,纹理图的QP分别设为25、30、35和40,深度图的QP分别设为34、39、42和45,每个视频序列包含3个纹理视频和3个深度视频,帧数取前100帧。实验测试性能指标采用峰值信噪比差(BD-PSNR)、比特率差(BDBR)(Bjontegaard,2001)和时间差(DT)等3项,其中BD-PSNR是指在相同实验条件下,在PSNR-Y客观视频质量方面的差异;BDBR是指在相同实验条件下,比特率降低比例;DT是指该方法相比标准测试软件HTM,在编码时间方面所节省时间的比例,其公式为:
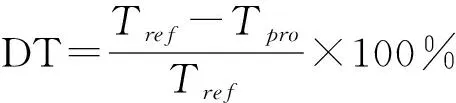
(6)
式中,Tref为标准测试软件HTM编码时间,Tpro为提出方法编码时间。
深度图的Hough变换方面,采用OPENCV库中的cvCanny(image,edges,threshold1,threshold2,aperture_size)函数检测深度图的边缘,其中5个参数分别指的是单通道输入图像、单通道存储边缘的输出图像、第一个阈值、第二个阈值、Sobel算子内核大小。为了尽可能多获得深度图的边缘信息,可将低阈值设置为20,高阈值设定为低阈值的3倍,取值为60,Sobel内核大小设定为3。
Hough变换采用OPENCV库中的cv::HoughLinesP(src,lines,rho,theta,threshold,minLineLength,maxLineGap)函数检测深度图的直线,其中7个参数分别指的是输入图像、输出的极坐标、生成极坐标时候的像素扫描步长、生成极坐标时候的角度步长、阈值、最小直线长度、最大间隔,其中rho取值为1,theta取值CV_PI/180,阈值指的是只有获得足够交点的极坐标点才被看成是直线,其取值为40,最小直线长度取值为15,最大间隔取值为10。
这与Jaballah等(2016)和李强等(2020)在思路方面类似,均通过检测深度图中的边缘信息,然后利用边缘信息跳过DMM模式的遍历,以及在不能跳过DMM模式的情况下仅选择少数几种DMM模式编码。因此,笔者选择与这2种方法进行性能方面的比较(表1)。
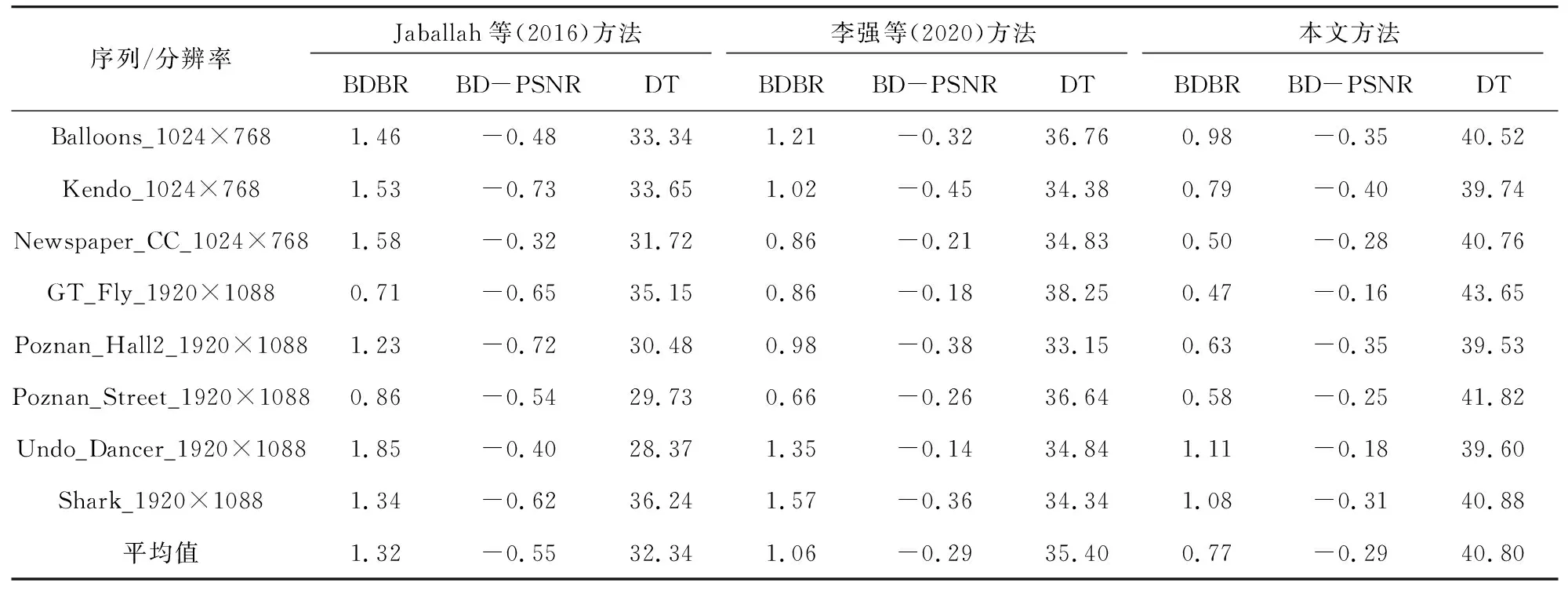
表1 全帧内预测模式下3种方法性能比较Table 1 The performance comparison of three methods on all intra mode
从表1的实验结果中可以看出,相比李强等(2020)、Jaballah等(2016)方法,笔者提出的方法在保持视频质量不变的前提下,视频压缩率有一定的提升,编码时间则有显著的降低,总体提升了性能。这主要因为本次研究采用Hough变换检测到的直线与DMM1模式中分割直线角度很接近,这带来了更小的编码误差,因此,在最终编码时比特率的上升也更少。同时,不仅跳过了许多情况的DMM模式,而且Hough变换检测到的直线与DMM1模式中分割直线角度近似。因此,在DMM1模式判决中仅需计算遍历5种模式,大大降低了编码时间。
4 结论
笔者提出了通过判决当前PU分块内部是否有直线从而跳过大量DMM模式的遍历计算过程方法。该方法在利用Canny算子检测边缘信息的基础上,根据Hough变换检测到的直线的位置和角度,给出了当前PU分块中DMM模式和DMM1模式的模式选择过程,有效跳过大量冗余的模式遍历计算复杂度。实验结果显示,相比目前主流快速模式选择方法,该方法能在保持视频质量和比特率的前提下,较大幅度地降低编码时间。
