关于Weyl编序的讨论*

张全胜，徐世民

(1.青岛西海岸新区致远中学，山东 青岛 266510; 2.菏泽学院物理与电子工程学院，山东 菏泽 274015)

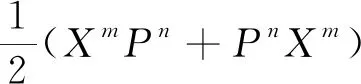
观点一 就经典函数xmpn来说，表示它的量子力学算符应是m个坐标算符X和n个动量算符P所有可能的排列等权重参与的平均[2,3]，即

(1)

其中Pi(m,n)表示这m个坐标算符X和n个动量算符P的第i种排列式. 譬如，一个坐标算符X和一个动量算符P，共有XP和PX两种排列，这两种排列等权重参与的平均是

(2)

又如，两个坐标算符X和两个动量算符P，共有X2P2、XP2X、XPXP、PXPX、PX2P、P2X2六种排列，这六种排列等权重参与的平均是

(3)

从(2)和(3)两式可以看出，其括号内X和P形式上是完全对称的、地位上是相同的.

若作进一步推广，那么，表示经典量xmpn+xkpl的量子力学算符应为

(4)

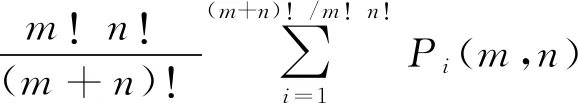
观点二 Weyl指出[4]，经典函数xmpn过渡到量子力学算符的规则为

(5)

从直观形式上来看，其算符排列特征与观点一有所不同、物理意义不够明确.

观点三 对于一般情况，Weyl还给出了一个积分型的对应规则[5]，可以表示为

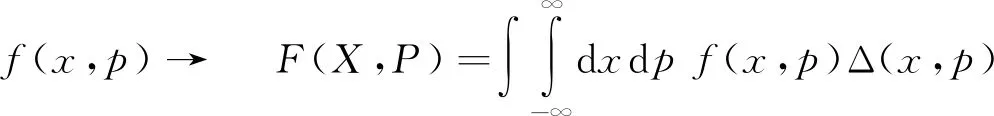
(6)

其中，F(X,P)是量子力学中表示经典函数f(x,p)的算符，而

(7)

称为Wigner算符[6]，这一对应规则称为Weyl-Wigner量子化方案.显然，牛顿-莱布尼兹积分法则不能直接适用这类积分，因为被积函数指数上含有不对易的坐标算符和动量算符.如果无视坐标算符和动量算符的不对易性，直接地应用牛顿-莱布尼兹积分法则完成积分，则会得到

Δ(x,p)=δ(X-x)δ(P-p)

(8)

或者

Δ(x,p)=δ(P-p)δ(X-x)

(9)

这两个结果都是错误的. 由此看来，涉及算符(狄拉克称之为q数)的运算问题，都是很复杂的，它跟普通数(称之为c数)有着很大不同，必须考虑算符的次序问题.

为了使得数学上表达与计算简单、牛顿-莱布尼兹积分能够顺利进行,更为了拓展物理应用，物理学家们创造了有序算符方法[7-9]，例如算符的正规乘积方法、反正规乘积方法、X-P排序方法、P-X排序方法以及外尔(Weyl)编序方法.尤其是Weyl编序，它是一种较为复杂的算符排序.

关于Weyl编序，我们发现不同文献也有着不同的定义. 例如，文献[3]按照观点一定义了Weyl编序，文献[10]按照观点二定义了Weyl编序，文献[11]按照观点三定义了Weyl编序.上述三种定义完全等价吗？究竟应该怎样定义Weyl编序才恰当呢？

定义是对一种事物的本质特征或一个概念的内涵和外延的确切而简要的说明. 定义一个概念，要突出本质特征、直观明了、意义明确，还要具有外延可拓展性.为此，作为更一般情形，考虑m个力学量算符A和n个力学量算符B的所有可能的排列等权重参与的情况，其平均为

(10)

这里Pi(A,B)表示这m个算符A和n个算符B的第i种排列式.设λ和ν是两个参数，对于n=0,1,2,3,…，逐一展开幂算符(λA+υB)n，会得到

(λA+νB)0=1

(11)

此式右端是零个A算符和零个B算符所有可能的排列等权重参与的平均.

(λA+νB)1=λA+νB

(12)

此式右端第一项是一个A算符和零个B算符所有可能的排列等权重参与的平均(确切地说，是该平均的倍，以下不再说明)；第二项是一个算符和零个A算符所有可能的排列等权重参与的结果.所以说，此式就是所有可能的排列等权重参与的结果.

(λA+νB)2=λ2A2+λν(AB+BA)+ν2B2

(13)

此式右端第一项是两个A算符和零个B算符所有可能的排列等权重参与的结果；第二项是一个A算符和一个B算符所有可能的排列等权重参与的结果；第三项是两个B算符和零个A算符所有可能的排列等权重参与的结果.所以说，此式就是所有可能的排列等权重参与的结果.

经过对n=3,4,5,6,…的情况进行认真仔细的观察与分析，我们发现(λA+υB)n本身就是所有可能的排列等权重参与的结果. 那么，任何可以展开为(λA+υB)n的幂级数的算符函数F(λA+νB)，其自身就是所有可能的排列等权重参与的结果. 特别是，指数算符函数e(λA+υB)，其自身就是所有可能的排列等权重参与的结果.

如果根据观点一来定义Weyl编序，亦即“算符A和B的所有可能的排列等权重参与的结果叫做关于算符A和B的Weyl编序”，并以符号┊┊标记之，约定：在此记号内算符A和B可对易，亦即可视作普通参数(c数)对待. 于是，Weyl编序就具有了一些性质，如

1)

┊F(A,B)+G(A,B)┊=┊F(A,B)┊+┊G(A,B)┊

(14)

2)c数可以自由进出Weyl编序记号┊┊；

3) 在记号┊┊内可直接进行c数的牛顿-莱布尼兹积分与微分运算，只要积分收敛.

据此可得

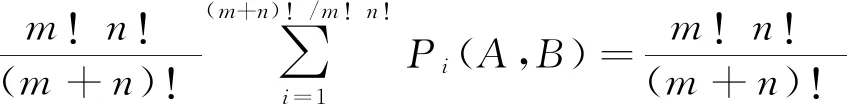
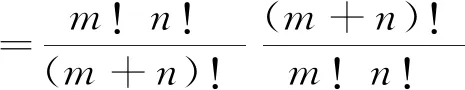
(15)

(λA+νB)n=┊(λA+νB)n┊

(16)

那么，对任何可以展开为(λA+υB)n的幂级数的算符函数F(λA+υB)，则有

F(λA+νB)=┊F(λA+νB)┊

(17)

特别是指数算符，有

eλA+νB=┊eλA+νB┊

(18)

注意，式(15)～(18)对A、B的对易关系没有任何要求，不受任何前提条件的限制.

依据式(15)，将算符A替换成坐标算符X、算符B替换成动量算符P，应用于观点一，便可得到经典函数xmpn的量子力学对应，即

xmpn→┊XmPn┊

(19)

依据式(18)，应用于观点三并在┊┊内完成牛顿-莱布尼兹积分，那么(7)式所示的Wigner算符也就可以写成

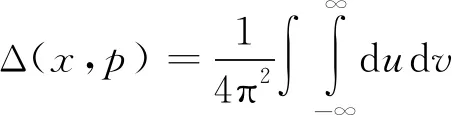
(20)

将此式代入Weyl-Wigner量子化方案并在┊┊内完成积分，便得到

F(X,P)=┊f(X,P)┊

(21)

这就是Weyl编序形式的Weyl-Wigner量子化方案.特别是当经典函数f(x,p)=xmpn时，则有

xmpn→┊XmPn┊

(22)

以上讨论以及式(19)和式(22)两式表明，观点一与观点三是相容的，观点一是观点三的一种特殊情形.注意，到目前为止我们并没有涉及到算符A和B的对易关系，也就是说，对任何两个量子力学算符A和B，观点一恒与观点三相容.

如果根据观点三来定义Weyl编序，也就是定义eλA+νB=┊eλA+νB┊或者Δ(x,p)=┊δ(X-x)δ(P-p)┊，尽管这与根据观点一来定义Weyl编序本质上一致，但这么做在形式上不直观、排序特征上不显然、物理意义上也不够明确.

(23)

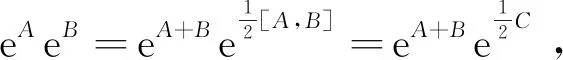
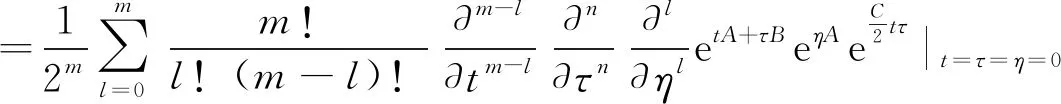
(24)

由式(18)可知e(t + η)A + τB= ┊e(t + η)A + τB┊.将其代入(24)式，得

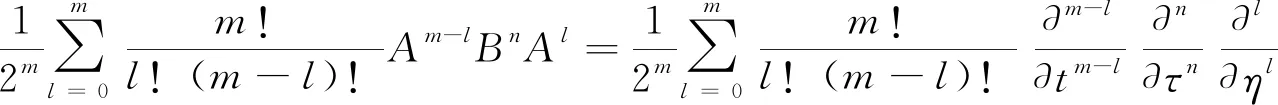
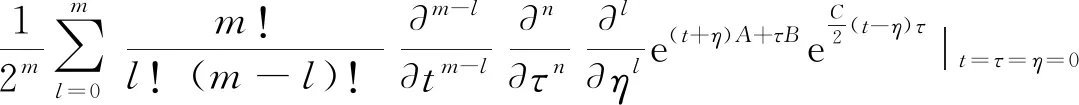
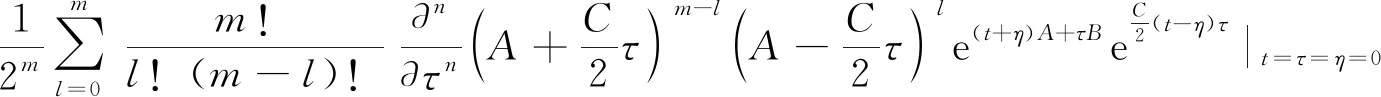
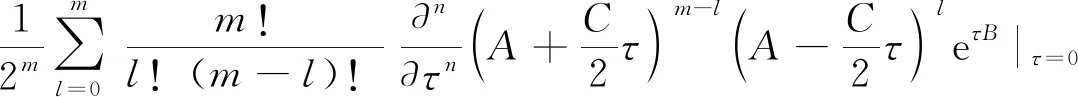
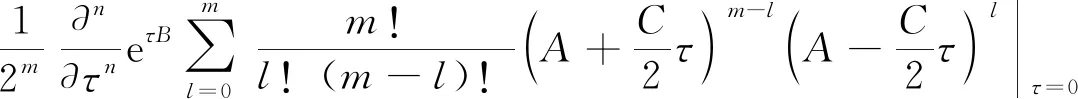
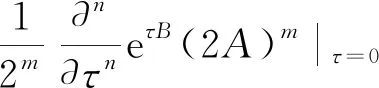
(25)

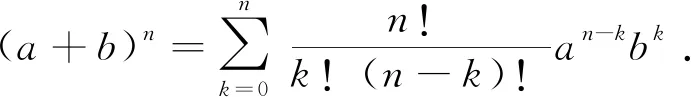
如果A、B的对易关系未知，或者说未有A、B的对易式跟A和B都对易的前提条件，那么就无法利用Baker-Hausdorff公式将式(23)中的三个指数算符的乘积合并成一个指数上是A与B线性组合的、形如eαA+βB的指数算符函数，也就无法利用式(18)得到算符etAeτBeηA的Weyl编序，因此也就得不出式(25). 这表明，对于一般的两个量子力学算符A和B来说，观点二与观点一和三不一致.

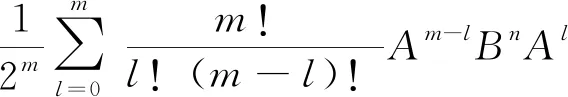
综上所述，我们认为，为了Weyl编序定义的本质特征显然,并且具有外延可拓展性，更为了能够利用这种有序算符方法简化Weyl-Wigner量子化方案的数学运算，应该按照观点一来定义Weyl编序，换言之，按照观点一来定义Weyl编序是最为恰当的.