基于迭代对称轴的准规则斑图基元分割
2021-11-20张梦玉
张梦玉


DOI:10.16644/j.cnki.cn33-1094/tp.2021.11.011
摘 要: 针对准规则斑图周期性的特点,创新的提出了一种基于迭代对称轴的准规则斑图基元分割方法。该方法以对称特征检测算法为基础,结合准规则斑图的对称轴及坐标,在确保基元图案完整的情况下,不断迭代对称轴坐标,直至得到包含完整最小基元的基元图案。实验结果表明,该方法能够较为准确的分割出基元图案,且不受准规则斑图构成形状的影响。当迭代对称轴次数为3次时,能够达到最佳的基元分割效果。
关键词: 准规则斑图; 对称特征; 基元分割; 迭代对称轴
中图分类号:TP391.4 文献标识码:A 文章编号:1006-8228(2021)11-41-03
Primitive segmentation of quasi-regular pattern based on iterative symmetry axis
Zhang Mengyu
(School of Information Science and Technology, Zhejiang Sci-Tech University, Hangzhou, Zhejiang 310018, China)
Abstract: Aiming at the periodicity of pattern in quasi-regular pattern, a method of pattern primitive segmentation based on iterative symmetry axis is proposed. This method is based on the symmetry feature detection algorithm, combined with the symmetry axis and coordinates of quasi-regular pattern. In the case of ensuring the integrity of the primitive pattern, the symmetry axis coordinates are iterated until the primitive pattern containing the complete minimum primitive is obtained. The experimental results show that the algorithm can segment primitive patterns accurately, and is not affected by the shape of quasi-regular pattern. When the number of iteration symmetry axis is 3, the best effect of primitive segmentation can be achieved.
Key words: quasi-regular pattern; symmetry feature; primitive segmentation; iterative symmetry axis
0 引言
准规则斑图是基于弱混沌动力系统通过哈密顿原理[1-2]計算得出的数学模型并通过计算机可视化后得到的图案。如图1所示,准规则斑图具有很强的重复性,许多准规则斑图都是由一个原始基元图案经周期性的平移、翻转获得的。这个构成准规则斑图的原始图案基元包含了整幅图案中的形状、颜色、纹理等特征。若能将准规则斑图中的基元图案分割出来,以基元图案作为整张准规则斑图的替代品用于预处理、特征提取等过程,能有效地减少计算资源的消耗,提高图案处理的效率。这种针对周期性原始图案基元分割对图案检索[3]等方面的研究具有显著影响。
基元分割技术的提出,主要是针对织物印花图案循环往复的特点。图案的基本单元中往往包含了整幅图案中必备的颜色、纹理、轮廓[4]。因此,在一些图案分析的过程中,常常将图案基元用作整幅图案的替代品,以减少计算资源的消耗,提高计算效率。Kuo等[5]利用模糊聚类算法对图案进行中的颜色和构成元素进行分类,再使用霍夫变换实现重复模式分割。Xiang等[6]提出利用自适应模版匹配技术进行图案的基元分割,此方法摆脱了传统的模板匹配算法对模板图案的依赖。然而,准规则斑图因其构成形状复杂多样,其基元图案往往不是只有一个形状构成,可能是由两种甚至多种几何形状组合而成。这使得现有的基于模版匹配的基元分割方法不能很好地适用于准规则斑图。
因此,本文针对准规则斑图具有明显的对称结构这一特点,利用对称特征检测算法[7],检测出准规则斑图的对称轴及对称轴坐标,再根据对称轴坐标选取合适区域进行图案分割。在分割后的准规则斑图上继续重复上一步骤,直到迭代的对称轴分割出最小基元图案为止。
1 算法实现过程
1.1 对称特征检测算法
本文从准规则斑图的对称结构入手,展开对基元分割方法的研究。采用基于Log-Gabor滤波器与颜色纹理特征相结合的对称特征检测算法对准规则斑图进行对称轴以及对称坐标的提取。
1.1.1 边缘检测与颜色-纹理直方图
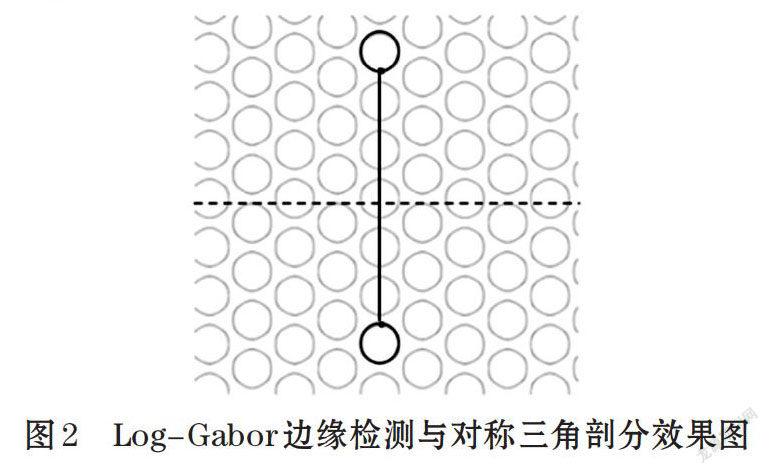
Log-Gabor滤波器是Gabor滤波器在傅里叶域的对数变换,通过将图案划分成多个部分[ei],从不同的角度和方向对图案进行边缘检测。这样多尺度的边缘检测能够更全面的检测到图案的边缘信息。如图2所示,经过Log-Gabor滤波器的边缘检测后,边缘段周围的纹理和色彩信息凸显出来,并使用纹理直方图[hi]和颜色直方图[gi]的来记录边缘图中包含的纹理和色彩特征。
1.1.2 对称三角剖分和投票
本文采用三角剖分的方法选择出处于对称位置的特征点对[(pi,pj)]。如图2所示,在图片顶端黑色圆圈的边缘所处部分[e1]中选取一个特征点[pi],在与它相对的底部黑色圆圈的边缘所处部分[e2]中,必存在一个点[pj]使得这两点间的连线(图2中黑色实线)上的所有点只有端点[pi]与[e1]间存在公共点。然后,根据特征点对应的纹理和颜色直方图求出该特征点对所对应的候选对称轴的权重[ωi,j],通过对称轴权重[ωi,j]来确定图案对称轴(图2中黑色虚线)。其具体定义如式⑴-式⑷。
其中:[τi=cosφi,sinφiT,R(T1ij)]是相对于直线的垂直线[(pi,pj)]的反射矩阵。由于[(pi,pj)]是一对对称的特征点,在已知特征点[pi]的纹理直方图[hi]的情况下,特征点[pj]的直方图[hj]只需将[hi]镜像翻转。
在本文中选取对称轴权重[ωi,j]排名前二的对称轴并记录其坐标,为后面进行基元分割区域的选择创造条件。
1.2 分割区域的选择
在进行准规则斑图基元分割时,既要保证分割的区域准确,不能破坏构成准规则斑图的图案基元;又要使分割区域尽可能的小。因此,在这里使用上一节中提到的对称特征检测算法,检测一张准规则斑图中的对称轴,并将对称轴进行可视化,如图3所示。
由图3可知两条对称轴将一张准规则斑图分割成了四个部分。被对称轴分割的部分中的基元构成和排列方式完全相同,因此我们只需选择任意区域作为图案切割。而为了计算方便在这里以准规则斑图的左上角部分作为切割区域。
利用对称特征检测算法,可以很轻松的得到每条对称轴端点所对应的坐标。在这里以图3为例,设图3中的两条对称轴的坐标分别为:横向虚线对称轴坐标为(x1,y1),(x2,y2);纵向虚线对称轴坐标为(x3,y3),(x4,y4)。要想实现图案切割,首先需要确定的是图案的左上角坐标,由两条对称轴坐标可以很明显的看出,A点的坐标为(x1,y3)。得到切割的初始位置后,接下来要计算出需要切割图案区域的长和宽。
由图3可知,需要切割图案的长为图中的纵向虚线,计算公式如⑸所示;同理,需要切割图案的宽为图中的横向虚线,计算公式如⑹所示。
到此為止,切割图案所需要的位置参数已经全部求出,完成了一次切割后的效果如图4所示。
相较于原准规则斑图,进行过第一次基元切割后的图案中元素数量明显减少,但仍然是由基元图案循环往复排列的。显然,仅仅进行一次分割是不能够完成分割出准规则斑图中的基元图案。因此,接下来需要找到合适的方法来实现准规则斑图的基元分割。
1.3 迭代对称轴坐标的基元分割
在上一节提出了根据准规则斑图的对称轴坐标进行分割,分割出排列形式和构成元素与原图案相似,但图案大小变小、图案中基元数量减少的准规则斑图分割图。然而,由于仅进行一次对称轴分割是完全不足以分割出准规则斑图中的基元图案。因此,在本节将采用迭代对称轴坐标的方式,进一步进行图案基元分割,最终得到准规则斑图的基元图案。
与第一次进行图案切割的步骤相同,将第一次切割效果图(图4)进行对称特征检测,同样可以得到如图3中的两条对称轴。根据对称轴的坐标,我们可以确定待切割图案的起始位置,再由公式⑶和公式⑷可以得到切割区域的长和宽。这样便完成了第二次切割。以此类推,不断对切割好的图案重复上述步骤,最终实现准规则斑图的基元分割。经过多次的实验尝试,最终将迭代次数设置为3次。
2 实验结果与分析
采用本文方法进行基元分割的结果如表1所示,主要展示了不同迭代次数下的基元分割效果。表中第一列展示的图片为准规则斑图的原图,后面三列分别展示了1-3次迭代分割后的效果图。显然,当迭代次数达到3次时,图中基本上只含有一个完整的基元图案。故将3次设置为基于对称轴坐标进行迭代基元分割的最终迭代次数。
与传统的模板匹配算法相比,本文算法省去了寻找匹配模板的麻烦,能够更方便地应用于各种场景中,如图像检索,作为图像检索过程中的预处理阶段,可以有效地降低图像的复杂度,增加特征提取的准确性和效率。
3 结束语
本文提出了一种基于迭代对称轴的准规则斑图基元分割算法,详细介绍了如何根据对称轴坐标选择分割区域,以及如何通过迭代对称轴坐标实现基元分割,并通过实验得出了能达到最佳分割效果的迭代次数。本算法根据准规则斑图的对称特征,不仅简化了图案信息,而且还保留了准规则斑图中主要的基元图案。
在基于迭代对称轴的准规则斑图基元分割的研究过程中,该算法对上下对称、左右对称的图案具有良好的分割效果,对其他对称类型,如中心对称,基元分割效果较差,在后续研究中需要改进。
参考文献(References):
[1] Zaslavsky G M, Sagdeev R Z, Usikov D A. et al. Weak Chaos and Quasi-regular Patterns[M].Cambridge:Cambridge University Press,1991.
[2] 汪秉宏.弱混沌与准规则斑图[M].上海科技教育出版社,1996.
[3] Doubek P, Matas J, Perdoch M, et al. Image Matching and Retrieval by Repetitive Patterns[A].2010 20th International Conference on Pattern Recognition[C]. Istanbul,Turkey:IEEE2010:3195-3198
[4] 何旋.印花织物循环图案基元分割与检索算法研究[D].浙江理工大学,2019.
[5] Kuo C, Shih C Y, Lee J Y. Repeat Pattern Segmentation of Printed Fabrics by Hough Trans-form Method[J].Textile Research Journal,2005.75(11):779-783
[6] Xiang Z, Zhou D, Qian M, et al. Repeat pattern segmentation of print fabric based on adaptive template matching. Journal of Engineered Fibers and Fabrics[J],2020.15(3):1-11
[7] Elawady M, Ducottet C, Alata O, et al. Wavelet-based Reflection Symmetry Detection via Textural and Color Histograms[A].IEEE International Conference on Computer Vision Workshop (ICCVW)[C].Venice, Italy: IEEE,2017:1725-1733
