基于超级电容混合储能系统的设计与分析

刘晓悦，陈 瑞，白尚维

(华北理工大学电气工程学院，河北唐山 063200)

随着世界经济与科技水平的迅速发展，人们对电能的需求愈来愈大，储能技术作为发电环节的关键技术之一，在电网中能带来巨大的实用价值和经济效益[1]。由于在电网中存在发电波动和负荷切换带来的电压波动，采用储能装置能够在一定程度上抑制功率波动，但单一的储能装置很难满足能量和功率的要求[2]。锂电池具有不宜频繁充放电、容量衰减、循环使用寿命低等缺点，而且由于一致性问题，锂电池很难组合。超级电容与其他储能装置相比，具有更高的功率密度，性能不随温度变化而变化，充放电速度快，适应能力较强，基本不需要人工维护[3-4]。因此，本文选择功率型储能装置超级电容器和能量型储能装置锂电池组成混合储能系统，充分发挥各自的优势，抑制功率波动，延长锂电池使用寿命。

文献[5]提出了一种钒电池和超级电容组成的混合储能系统，根据储能设备的荷电状态(SOC)分级优化控制，实现了对风电功率波动的平抑。文献[6]提出了一种自适应模糊控制策略，对功率目标值进行修正，有效避免了混合储能设备的过充过放，延长了使用寿命。文献[7]采用一阶低通滤波的方法平抑微电网的输出功率，通过模糊控制算法优化分配功率指令。文献[8]利用小波包分解法和模糊控制方法对蓄电池和超级电容的功率进行了修正，最终达到对风力发电系统并网时功率波动的平抑。本文将自适应变异粒子群(AMPSO)算法与BP 神经网络相结合，对锂电池的荷电状态进行估计，提出了一种超级电容锂电池并联的混合储能系统，采用模糊控制算法控制功率变换器的占空比，在Matlab/Simulink 中搭建了仿真模型，实验结果验证了本文所提方法的有效性。

1 AMPSO-BP 神经网络锂电池荷电状态估计

1.1 自适应变异粒子群算法

粒子群优化算法(PSO)是Kennedy 和Eberhart 提出的一种算法，可以增大找到全局最优解的几率。每个粒种随机迭代优化算法，传统的PSO 算法具有容易提前收敛、局部寻优能力较差、收敛速度慢等不足，且容易陷入局部最优值。因此，在AMPSO 中加入变异程序，按照一定的概率再次初始化部分粒子，其中，针对局部小范围寻找最优的进化子的位置和速度由以下公式确定：

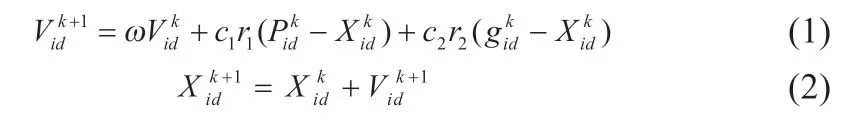
式中：k为当前迭代次数；ω 为惯性权重；Vid为粒子速度；Pid为粒子目前搜索到的最佳位置；d=1,2…,D；i=1,2,…n；gid为整个粒子群目前搜索到的最优位置；c1、c2为加速度因子；r1和r2表示[0,1]的随机值。

ω 的大小由最优适应度值fi来决定，其关系表达式为：

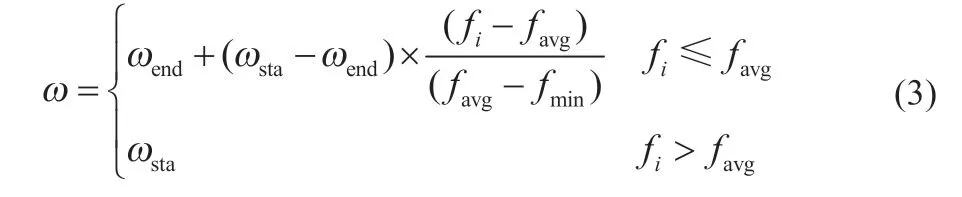
式中：favg、fmin分别为当前种群的平均适应度值和最小适应度值。

动态地调整粒子的飞行时间能有效解决陷入局部极值的缺点，其调整公式如下：

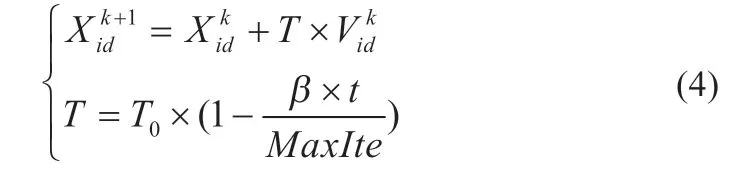
式中：β 为比例调节因子，一般取值为0.9；T为粒子的飞行时间；t为粒子迭代次数；MaxIte为粒子最大迭代次数；T0为初始飞行时间，取T0=0.9。

1.2 锂电池荷电状态估计

锂电池正常工作时可被看作是高度非线性的系统，而神经网络是一个非线性映射系统，并且不需要建立数学模型，给定输入就能得到输出，可以很好地模拟电池动态特性。选取锂电池组的电流、电压、温度这3 个变量作为神经网络输入，锂电池的SOC作为网络的输出[9]。根据分析建立一个3-20-1 结构的网络模型。

Advisor[10]是一款分析性软件，它的各种部件模型可以轻松扩展和改良。为了更好地估算锂电池的SOC，选取美国公司的GM_EV1 型号的电动车，电池组(96 节SAFT 锂离子电池)容量为100 Ah，锂离子电池总电压为344 V。

本实验设置初始SOC为60%，训练好神经网络后，利用CSHVR 工况数据进行SOC预测，基于自适应变异粒子群算法与BP 神经网络的估算结果如图1～2 所示，基于AMPSOBP 神经网络的锂电池SOC估算误差基本保持在2%以内，表明基于AMPSO-BP 的锂电池荷电估计方法可行，并具有良好的预测效果。

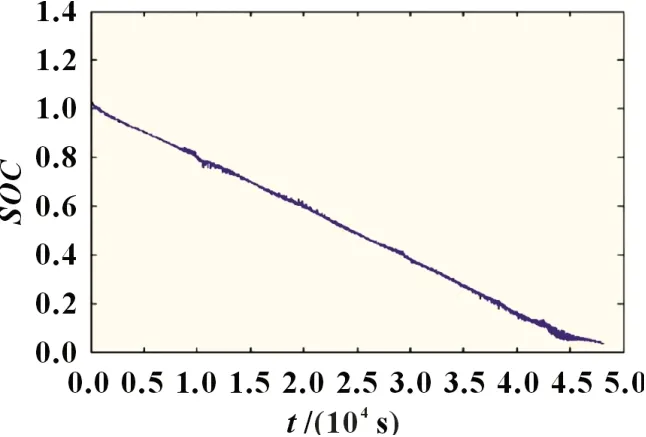
图1 工况下SOC估算结果

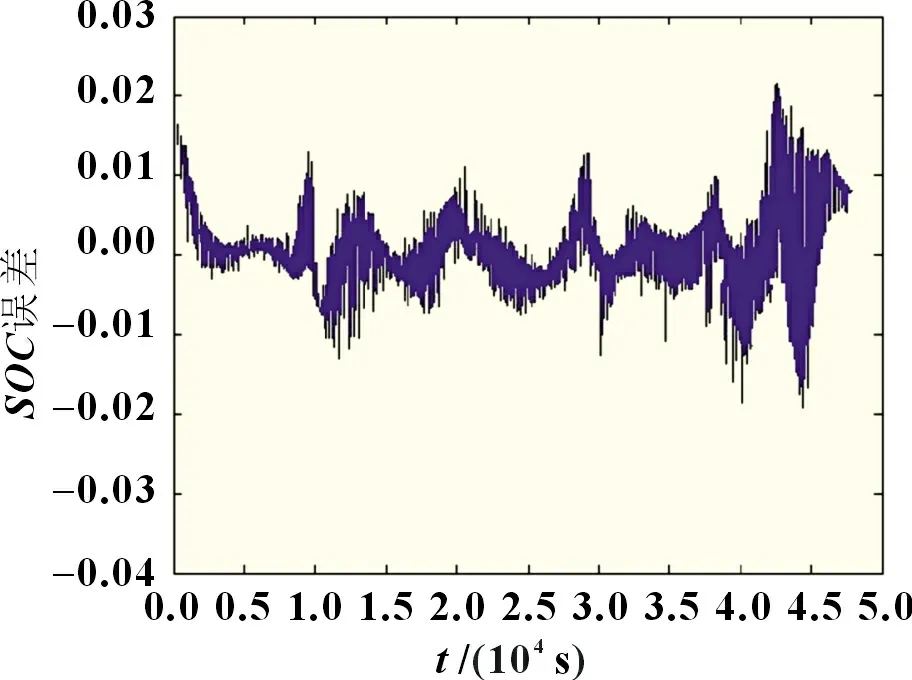
图2 电池SOC估算误差

2 混合储能系统的构建

2.1 混合储能系统的数学模型

在混合储能系统中，锂电池通过Boost 功率变换器给负载供电，作为系统的主要供电单元，超级电容器与双向DCDC 功率变换器相连。当负载发生变化，功率快速升高，直流母线电压下降。由于模糊控制器能够迅速调整功率变换器开关管占空比，从而使直流母线电压稳定在一定范围内，有效抑制了功率波动。超级电容器功率密度高，在负载骤增时，超级电容器会迅速地补偿负载需要的功率，避免了锂电池大电流放电，保障了锂电池的安全及使用寿命。

图3 为混合储能系统的电路图及等效电路模型。其中，Rc、Rb分别为超级电容器和锂电池的等效内阻，C、Ub为超级电容器等效电容和锂电池电压。

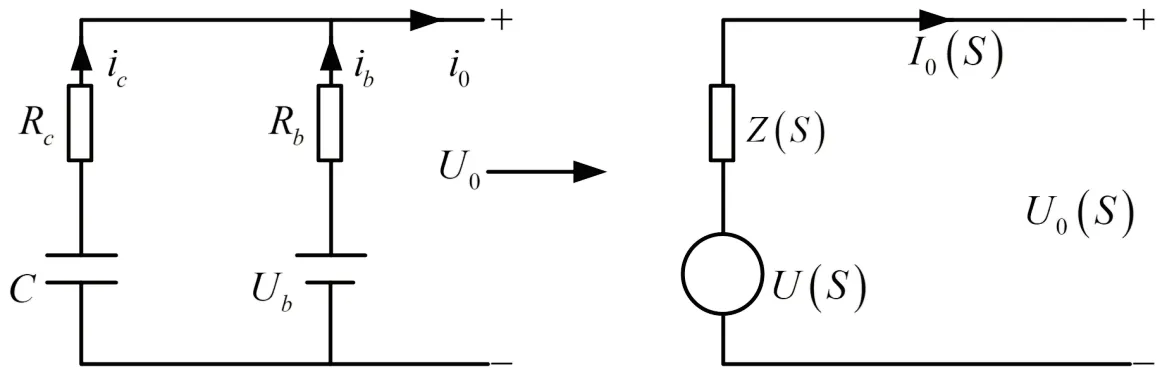
图3 混合储能等效电路模型

由戴维南等效定理，可得：

2.2 模糊控制器的构建

模糊控制由模糊化、模糊推理、清晰化三部分组成，图4为模糊控制的基本流程图。

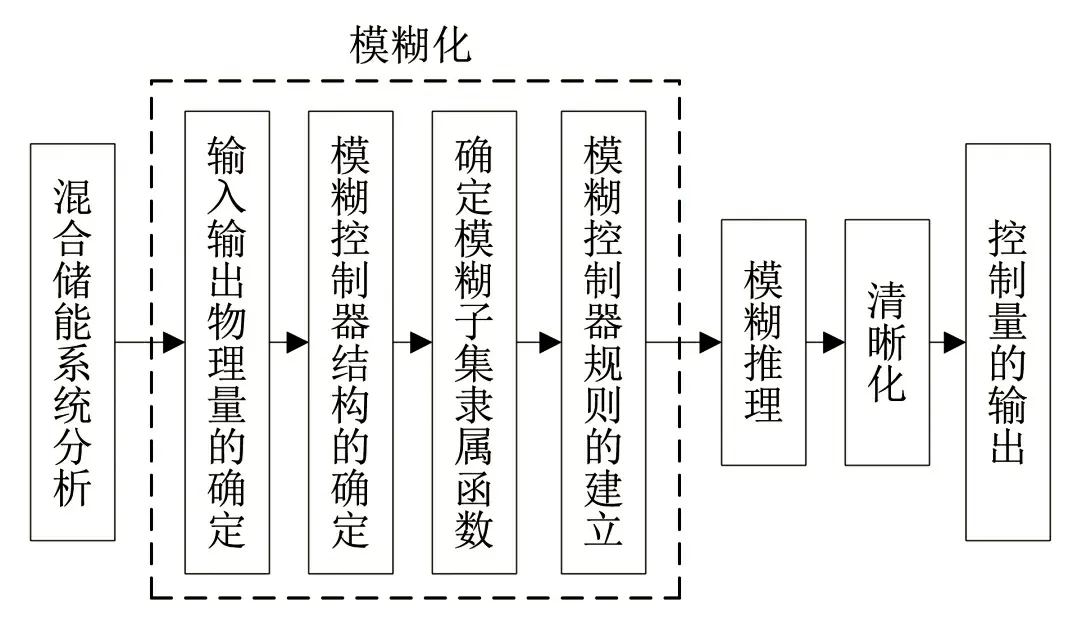
图4 模糊控制流程图

模糊控制器有2 个输入量，分别为母线电压与基准电压之间的差值V及电压的变化率E，将V和E的值从小到大分别转换成对应的模糊子集{NB,NS,ZE,PS,PB}，基准电压为DC48 V。将双向功率转化器的占空比D作为输出模糊变量，输入输出量模糊化的隶属度函数均选择三角形隶属函数。

模糊推理的公式为：

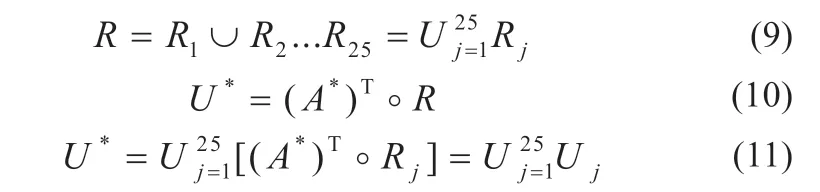
式中：A*和U*分别为输入量及输出量的矩阵形式；符号“。”表示合成算法。经过计算，共需25 个模糊规则。

去模糊化，将模糊集合转换成精确的数值，本文选用面积中心法，公式为：

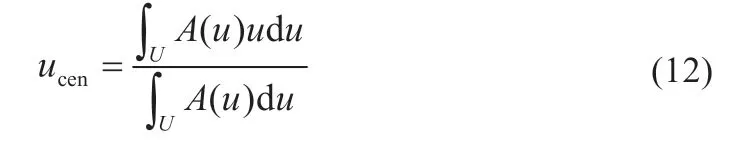
式中：A(u)为隶属函数，uϵU；ucen为中心横坐标。

2.3 脉冲发生器的构建

由于在Matlab 中没有现成的占空比可调的脉冲发生器，本文根据波形变化与三角形相似原理，构建脉冲宽度可调的脉冲发生器，如图5 所示，脉冲发生器包括比较器、三角波信号以及绝对值模块等。通过改变比较器的输入值来控制脉冲宽度。

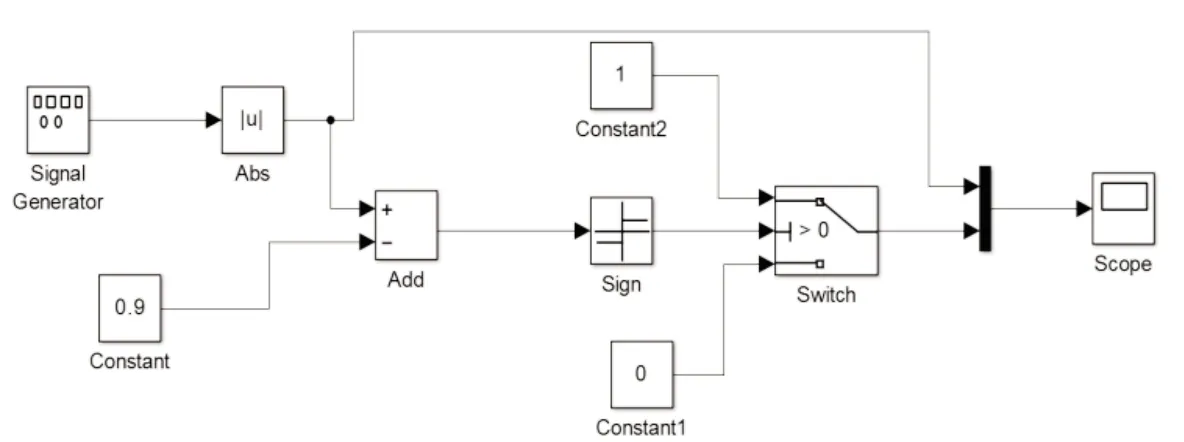
图5 可调脉冲发生器结构图

3 仿真结果分析

图6 为锂电池超级电容混合储能系统仿真图。混合储能系统由锂电池超级电容并联电路、模糊控制器、可调脉冲发生器、电阻、电感、双向DC-DC 变换器等构成。混合储能系统的参数设置如表1 所示。混合储能系统的锂电池和超级电容器的内阻分别为20、16 mΩ。系统输出功率最高为5 kW，时间为10 s。

图6 混合储能整体仿真图

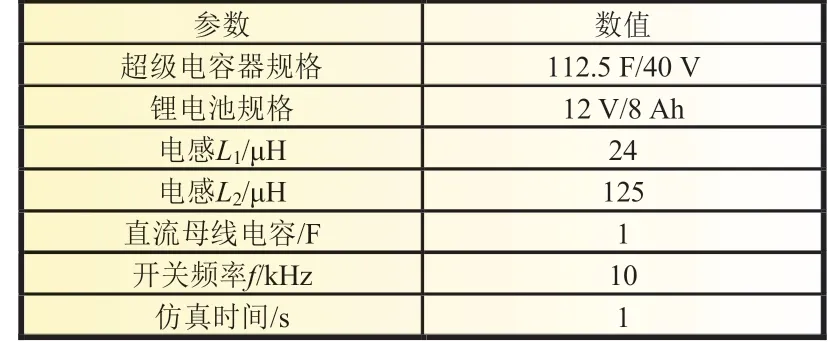
表1 混合储能系统参数设置

为了验证混合储能系统结构和控制策略的有效性，在Matlab 中进行Simulink 仿真实验，充满电后在放电过程中得到直流母线电压、锂电池电流以及超级电容器电流波形，如图7～9 所示。

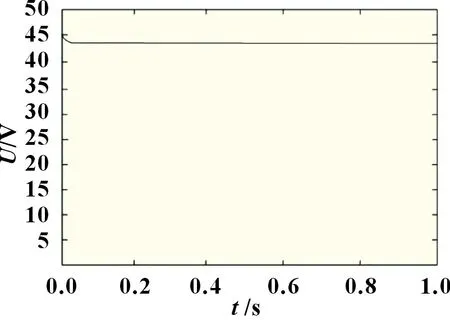
图7 直流母线电压曲线

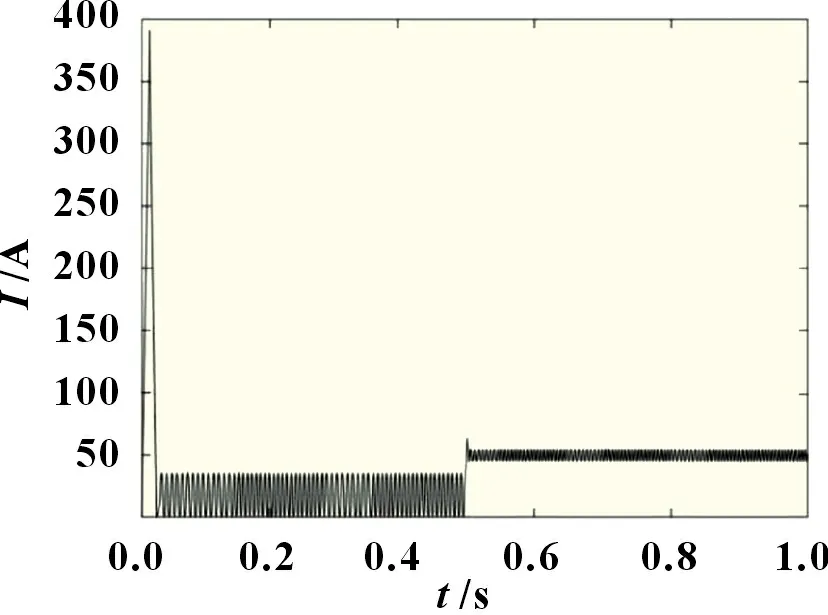
图8 锂电池电流曲线

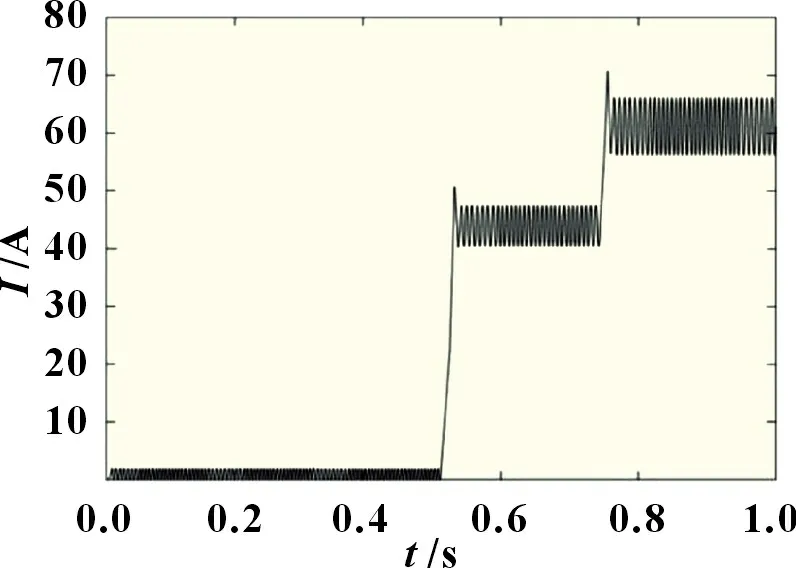
图9 超级电容电流曲线

由图7～9 可知，在混合储能系统中，整个仿真时间分为三个阶段：第一阶段(0～0.5 s)，设置负载电阻的值为10 Ω，混合储能系统低功率运行，锂电池提供负载所需的能量；第二阶段(0.5～0.75 s)，负载电阻突变为1 Ω，系统以高功率运行，超级电容很快补偿功率突变瞬时所需的功率，提供了负载功率突变部分，避免了负载突变对锂电池的冲击，由于在模糊控制器的作用下，锂电池电流能很快稳定下来，避免了系统震荡；第三阶段(0.75～1 s)，超级电容器大功率放电导致储能减少，电压降低，在模糊控制器的调节作用下，维持输出电压稳定，同时输出电流上升来保持高功率输出。

4 结论

本文利用工况数据进行了SOC预测，采用AMPSO 算法对BP 神经网络参数进行了优化，建立了基于AMPSO-BP 神经网络的锂电池SOC估算模型，并提出了基于模糊算法的混合储能控制策略，并搭建了超级电容器、锂电池混合储能系统模型。仿真结果表明，所提的模糊控制算法能够有效地控制功率变换器开关管占空比，维持了母线电压的稳定，混合储能系统结合了两种储能元件的优缺点，有效地避免了锂电池大电流放电，延长了锂电池使用寿命。