基于圆弧主应力迹线的黏性土主动土压力分析
2021-11-20王佳宇曹文贵王雨波张慧姐
王佳宇,曹文贵,王雨波,张慧姐
(湖南大学土木工程学院,湖南 长沙 410082)
挡土墙后土压力的计算一直是土力学研究的重点问题,明确作用于挡土墙上土压力的大小和分布,对于挡土墙设计具有重要的工程实际意义。自从18世纪朗肯和库仑土压力方法理论创建以来,其凭借参数清晰、计算模型简单等优点被广泛使用,并逐渐成为土压力分析研究中的两大经典理论。但经典理论并不完美,存在明显的不合理之处,朗肯理论假定墙背竖直光滑得到墙后土体沿墙高呈线性分布的规律,没有考虑墙土摩擦角对土压力的影响;库仑理论对于整体土楔体建立平衡方程,仅能得到土压力合力,无法获得土压力沿墙高的分布,该理论也不适用于黏性填土。
针对经典理论的不足,众多学者对土压力问题进行了大量的后续研究工作。目前研究挡土墙后黏性土土压力主要有两种思路:其一,基于库仑块体极限平衡理论,考虑墙背接触面和滑裂面上黏聚力的影响,对滑动土体建立整体静力平衡方程,求解得到复杂情况下墙后土体土压力的合力表达式[1−5]。但该方法仍无法获得土压力沿墙高的分布规律;其二,考虑土拱效应的影响,基于薄层微分单元研究土压力分布的规律。目前,运用最多的分层方法是水平分层[6−15],将墙后土体划分为无数水平薄层,假定层面上分布等效均匀竖向应力,通过对薄层单元进行受力分析,进而得到土压力分析方法。这类方法计算模型简单直观,得到了土压力非线性分布的表达式,但该方法忽略水平层上下截面的剪应力、假定竖向应力均匀分布,存在明显的不足。通过对土拱效应的深入研究,Li 等[16]和Cao 等[17]提出了沿主应力迹线割线分层的新理论,近似认为主应力迹线为倾斜直线,在分层截面上只分布主应力,没有剪应力,简化了受力分析,但该方法只是一种近似处理,不符合实际受力情况。Cao 等[18]在此基础上提出沿主应力迹线分层的方法对土压力进行平衡分析。由于薄层单元是按主应力轨迹进行划分的,所以层间只作用大主应力而没有剪应力,有效避免了直线分层的不足,为土压力分析开拓了新的思路,经验证取得更为合理的结果。但是,目前基于主应力迹线分层方法还仅局限于无黏性土的研究,不适用于黏性填土的分析,且主应力迹线几何形状、几何参数确定较为复杂,这正是本文研究的主要内容。
综上所述,本文基于主应力迹线分层的土压力分析方法,充分考虑了黏聚力对土压力分析的影响,取曲线薄层微分单元为研究对象,合理分析曲线单元受力情况,建立静力平衡关系,推导得到黏性土土压力的分布、合力及作用点高度计算的新方法。
1 应力偏转规律及应力状态分析
1.1 基本假定
如图1所示,挡土墙高为H,ABG是处于主动极限状态下的三角形土楔体,土体为黏性土,靠近墙顶附近区域的土体ABCD在自身黏聚力和内摩擦角的作用下保持稳定,土体内部形成张拉裂缝,裂缝深度为z0。鉴于实际挡土墙土压力问题的复杂性,为了方便研究,进行以下假定:
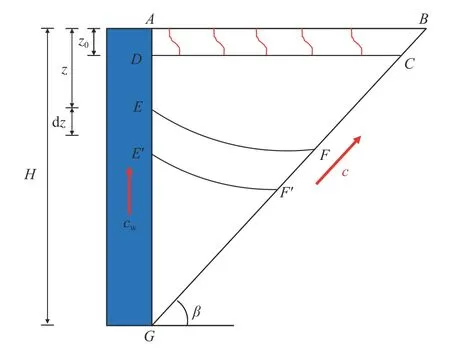
图1 土楔体及主应力迹线模型Fig.1 Soil wedge and principal stress trace model
(1)挡土墙竖直,墙背粗糙,填土面水平且无附加荷载,墙土摩擦角为δ;
(2)挡土墙后土体为黏性土,内摩擦角为φ,墙土接触面处黏聚力为cw,土体黏聚力为c,且满足cw=ηc,其中η=tanδ/tanφ;
(3)挡土墙背离土体发生平动位移时,靠近墙顶附近区域土体内部形成张拉裂缝,其深度可用下式计算[1−5]:
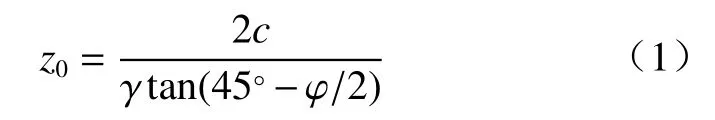
式中:γ—土体重度。
(4)假定挡土墙后土体主动极限状态下滑裂面为直线,倾角为β,大小依据文献[1]的理论结果进行计算:
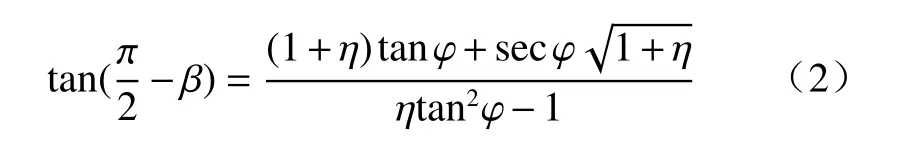
(5)为了方便研究黏性土土体应力状态变化的情况,引进文献[15]中坐标平移的方法。将图2所示莫尔应力圆中的纵坐标τ向左偏移ccotφ距离,新旧坐标系之间的关系可表示为:
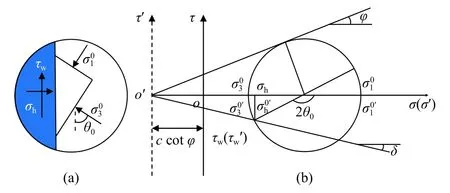
图2 墙土接触面受力分析和莫尔圆情况Fig.2 Deflection of the principal stress and Mohr circle at the contact surface of the wall back
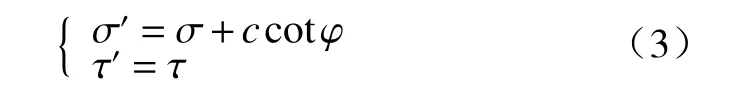
式中:σ 、τ—旧坐标系中的横、纵坐标轴;
σ′、τ′—新坐标系中的横、纵坐标轴。
1.2 应力偏转及应力状态分析
实际挡土墙工程中不存在绝对光滑的情况,墙土之间的摩擦力导致墙土接触面主应力方向发生偏转,进而引发其他土体微分单元的主应力发生偏转,直到土体破裂面处停止。Handy[6]基于土拱效应把土拱形状定义为主应力迹线,认为即使主应力方向发生偏转,土体内仍存在相互垂直的大小主应力迹线。由于本文研究主动极限状态下土压力变化规律,故引入小主应力迹线模型,如图1所示。
在墙背粗糙的影响下,主应力方向发生了偏转。图2(a)表示深度为z时墙土接触面E点处土体单元受力状态。两直角边上分别作用有最大主应力和最小主应力,最小主应力方向由原来的水平偏转为与竖直方向呈θ0角度;斜边与墙背重合,作用有正应力 σh和剪应力 τw。假设墙土接触面处于极限平衡状态,则该点土体的大小主应力满足以下关系:
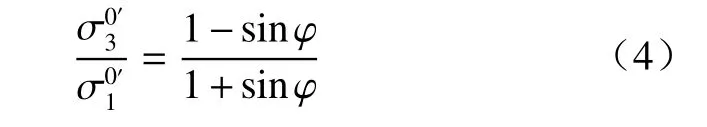
根据图2(b)莫尔应力圆可得应力表达式为:
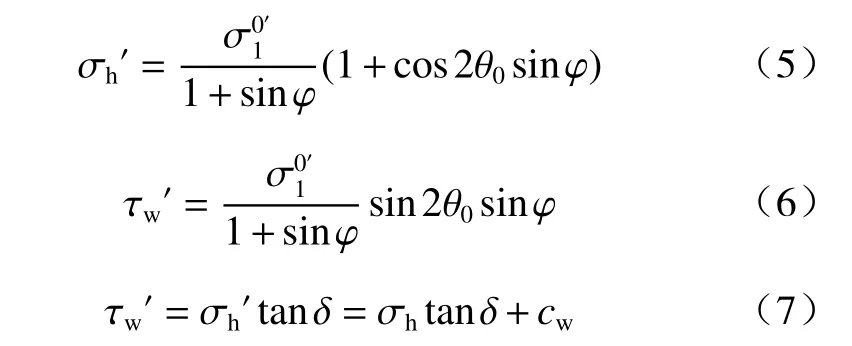
联立式(5)(6)(7)可得墙土接触面小主应力偏转角表达式为:
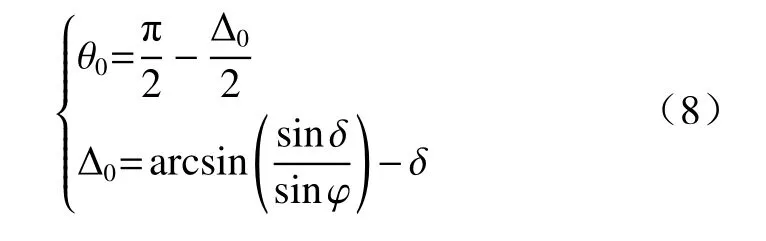
图3所示为滑裂面F点处土体单元受力状态。两直角边上分别作用有最大主应力和最小主应力最小主应力方向偏转为与竖直方向呈θ1角度。当土体达到极限平衡状态时,大主应力作用面与滑裂面夹角为ψ=45°+φ/2,因此主应力偏转角θ1表达式为:
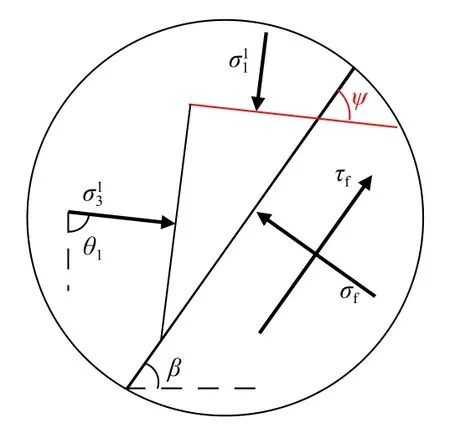
图3 滑裂面处主应力偏转情况Fig.3 Deflection of the principal stress at the slip surface

由式(8)(9)可知墙背接触面和滑裂面上主应力偏转角θ0、θ1与埋深无关,只与墙土本身的属性有关,即在墙上任意深度处,主应力偏转角均相等。但在同一条主应力迹线上的不同位置处,主应力偏转角不同。
2 土压力公式计算
2.1 主应力迹线几何形状、参数确定
为深入分析挡墙后土拱效应对土压力的影响,众多学者针主应力迹线形状进行了探讨,分别有假设主应力迹线形状为悬链线、圆弧、抛物线、对数螺旋线等。应宏伟等[8]经过理论推导、对比分析发现,主应力迹线形状对土压力强度大小及分布影响较小。为简化研究思路,本文采用圆弧小主应力迹线形式,土楔体在墙背摩擦角的作用下主应力发生偏转,土体内形成无数圆弧主应力迹线,取其中一段微分单元EFF'E'为研究对象,如图4所示。圆弧上E点与圆心的连线与水平方向的夹角为θ0,F点与圆心的连线与水平方向的夹角为θ1,主应力迹线i位置处与圆心的连线与水平方向的夹角为θi。为了获得曲线微分单元EFF'E'的受力分析,首先需要确定圆弧的几何位置和参数,求解圆弧半径过程如下:
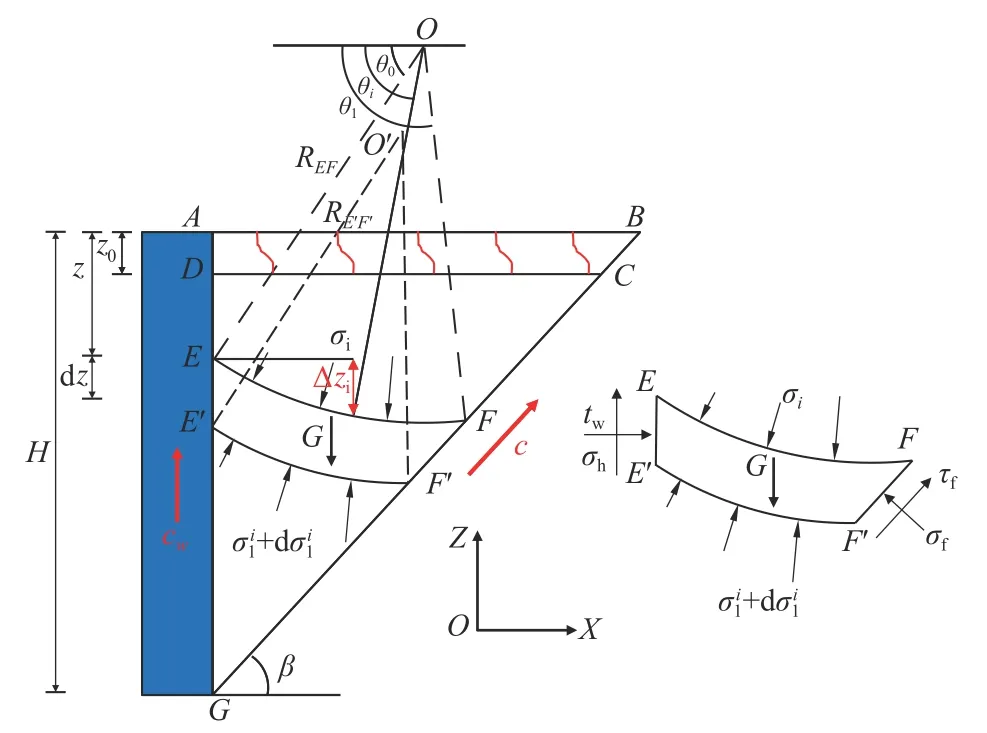
图4 主应力迹线分层模型及薄层单元受力分析Fig.4 Layered model of the principal stress trace and force analysis of thin-layer elements
建立直角坐标系:G为原点,竖直方向为z轴,水平方向为x轴,E点坐标为(0,H−z),设F点横坐标为x0,根据直线方程可知其纵坐标z0=x0tanβ,圆弧主应力迹线上E、F两点满足下列几何关系:

2.2 主动土压力强度计算






2.3 土压力合力及其作用点高度计算

3 实例验证与参数分析
3.1 实例验证
为了验证本文方法的正确性,选取文献[19]中的实验数据对本文结果进行验证。该实验墙背竖直,墙高为4 m,土的天然重度为γ=18.95 kN/m3,不排水三轴快剪指标为内摩擦角φ=16.6°,土与墙间摩擦角δ=8.3°,黏聚力c=4.6 kPa。
图5 给出了本文方法与实测数据和其他理论方法的对比结果。由图5 可知,本文方法和文献[11][12]均得到了土压力强度沿墙高呈非线性分布的规律,在接近墙脚位置处的应力值发生突变。本文方法和文献[12]计算结果始终小于朗肯理论计算值,文献[11]在挡土墙上面一部分略大于朗肯理论计算值,偏于保守,下面一部分小于朗肯理论计算值 。从数据对比分析来看,本文方法计算结果无论从大小还是分布均与实测结果更加吻合,验证了本文方法的合理性及优越性。
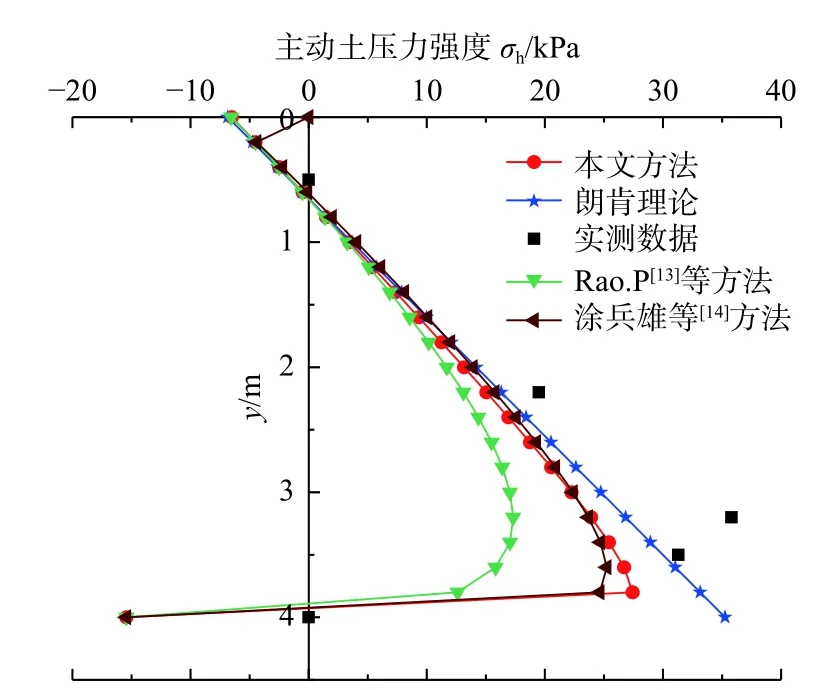
图5 主动土压力对比分析Fig.5 Comparative analysis of active earth pressure
3.2 参数分析
为了更深入地探讨各参数对黏性土主动土压力分布的影响,选取工程中常用的参数范围,通过控制变量法,从定性的角度总结墙土摩擦角-内摩擦角(δφ)、黏聚力c等因素对土压力强度分布的影响规律。
图6 表示墙土摩擦角δ对土压力分布的影响,由图6 可知,随着δ增大,土压力逐渐减小。δ值较小时,土压力近似呈线性分布,在接近墙踵处突变为负值。δ逐渐变大,土压力分布从近似直线变为曲线分布,应力突变点逐渐提高。如图7所示,始终保持δ/φ=2/3,随着φ增加,土压力不断减小,塑性临界深度逐渐增大。图8 表示黏性土黏聚力对土压力分布的影响,随着土体黏聚力c增加,土压力逐渐减小,塑性临界深度逐渐增大。
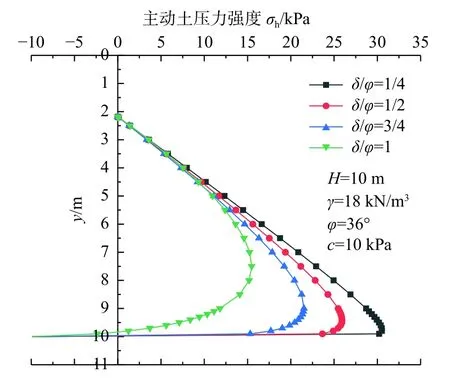
图6 墙土摩擦角δ 对土压力分布的影响Fig.6 Influence of the wall-soil friction angle on earth pressure distribution
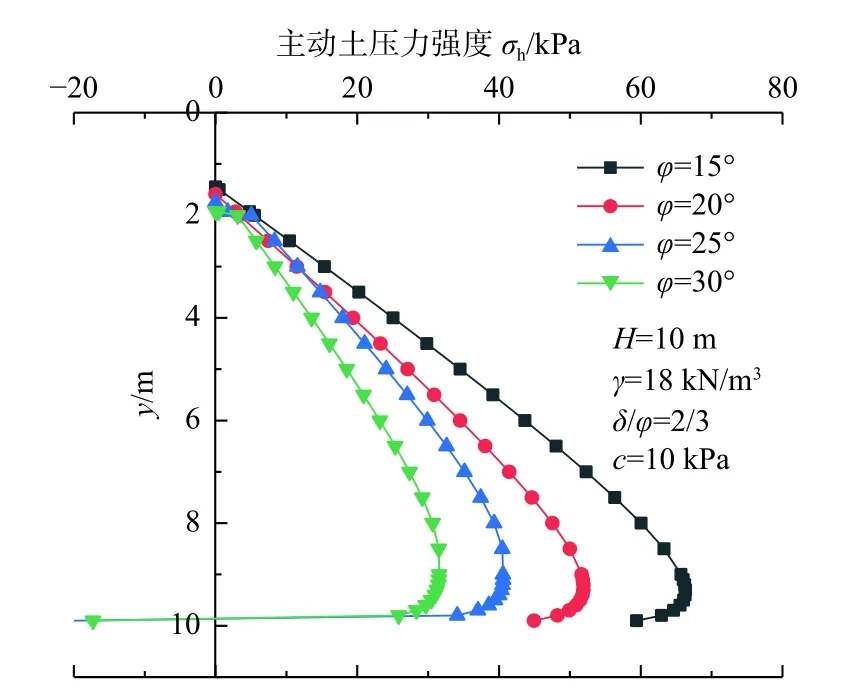
图7 土体内摩擦角φ 对土压力分布的影响Fig.7 Influence of the friction angle in soil on the distribution of earth pressure
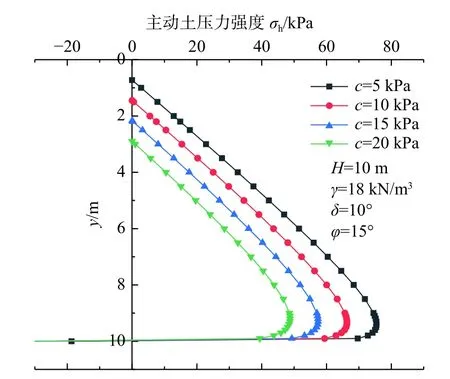
图8 黏聚力c 对土压力分布的影响Fig.8 Influence of cohesion on the distribution of earth pressure
图9 表示土体内摩擦角对侧向土压力合力的影响,朗肯理论合力表达式只与φ相关,当φ为定值时,合力即为定值;随着δ增加,本文方法与文献[7]方法合力逐渐减小,这是由于墙土间摩擦力可抵消一部分土压力,因此合力减小,与实际情况相符合。图10 表示墙土摩擦角对合力作用点高度的影响,随着δ增大,本文合力作用点高度缓慢升高,挡土墙整体稳定性变差;而文献[7]合力作用点近似直线上升趋势,与朗肯理论作用点结果偏差太大,故本文计算结果更加具有合理性。
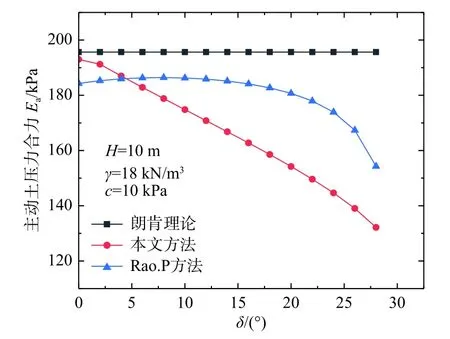
图9 墙土摩擦角δ 对土压力合力的影响Fig.9 Influence of wall-soil friction angle on the resultant force of earth pressure
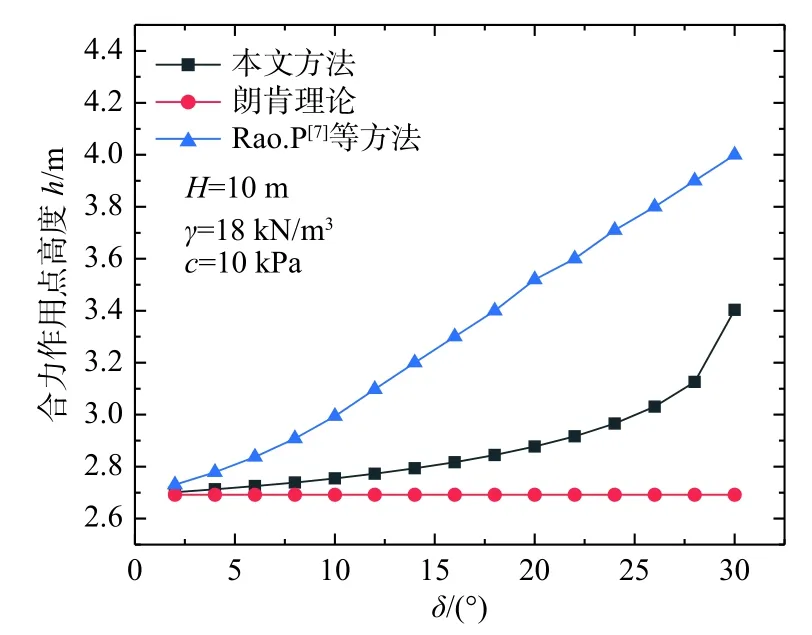
图10 墙土摩擦角δ 对土压力合力作用点高度的影响Fig.10 Influence of wall-soil friction angle on the height of the resultant point of earth pressure
4 结论
(1)通过与实测数据和现有的理论方法进行土压力大小和分布规律的对比分析,验证本文方法的合理性及优越性;从定性的角度分析了墙土摩擦角、土体内摩擦角、黏聚力等因素对土压力强度分布的影响规律及影响程度。
(2)研究结果表明:黏聚力对土压力大小有明显的影响,随着黏聚力的增加,土压力逐渐减小;墙土摩擦角δ较小时,土压力线性分布特征越明显,随着δ增大,土压力合力逐渐减小,合力作用点缓慢提高,土压力分布逐渐减小且非线性分布特征越明显。
(3)由于本文研究中假定张拉裂缝为朗肯裂缝,没有考虑墙背粗糙程度对裂缝深度的影响,比实际工程测得的裂缝高度偏低一点,对研究结果的适用性有一定的影响,因此对裂缝深度的计算还需有进一步的研究。
