SIMON算法相关密钥不可能差分特征搜索*

王旭姿,吴保峰,侯 林,林东岱

1.中国科学院 信息工程研究所 信息安全国家重点实验室,北京 100093

2.中国科学院大学 网络空间安全学院,北京 100049

1 引言

近些年来,随着物联网和人工智能的迅速发展,人们生活中出现了越来越多的小型便携设备,这些设备虽然计算资源受限,但由于其传输的信息涉及个人隐私越来越多,所以对安全性要求反而更高.另外随着5G网络的日益普及,对加密算法的软硬件实现速度也有着越来越高的要求,传统的加密算法已无法满足需求.因此各个国家都开始着手征集和制定轻量级分组密码算法标准,其中美国NSA于2013年发布的SIMON算法和SPECK算法[1]由于其优秀的软硬件实现性能引起了广泛的关注.2015年Yang等人于CHES发表SIMECK算法[2],将SIMON循环移位参数由(8,1,2)改为(0,5,1),并在密钥扩展算法中重用轮函数代替SIMON的线性密钥扩展算法,使其软硬件实现速度更高效.

目前,学术界已有非常多对SIMON和SIMECK算法单密钥下的安全性分析结果,如差分分析[3-7]、不可能差分分析[8-12]、线性分析及零相关线性分析[13-15]和积分分析[16,17]等.但相关密钥条件下的安全性分析非常有限,SIMON算法设计者在文献[18]中也提到了这一点,而SIMECK算法相关密钥条件下安全性依赖于SIMON算法在该条件下安全性分析结果[2].截至目前只有文献[19]中给出了SIMON和SIMECK相关密钥下高概率差分长路径,文献[20]中给出了SIMECK在输入输出差分均只有1比特活跃条件下的相关密钥不可能差分特征.而SIMON和SIMECK算法相比较,不同点就在于循环移位参数的改变和密钥扩展算法由线性变为非线性,研究其密钥扩展算法对安全性的影响是非常有必要的.为了应对资源受限条件下对高速加解密的需求,美国NIST正在征集轻量级密码算法标准,截至目前第二轮候选算法中有三个算法采用了SIMECK轮函数作为底层置换算法[21-23],分别为ACE、SPIX和SpoC,在此底层置换基础上不仅实现加密和解密功能,也同时提供了MAC和HASH功能.结合SIMON和SIMECK算法安全性分析现状,进一步研究其相关密钥条件下的安全性是当前急需解决的问题.在表1中总结了SIMON32/64和SIMON48/96当前已有区分器对应的概率和包含的轮数,并与本文结果对比.

目前对分组密码算法进行安全性分析时,使用的自动化搜索工具主要为MILP、SAT、SMT/STP等.这些工具的搜索效率受维数影响很大,特别是当前轻量级分组密码算法几乎都是基于比特运算的,即使是单密钥下路径搜索,随着轮数的增加,搜索速度降低也非常明显,无法在此基础上直接进行相关密钥下路径搜索.对不可能差分特征的搜索,需要限制输入输出差分均只有1比特或1个S盒活跃,在此基础上找出概率为1的截断差分路径,当中间某一轮中某个比特位的差分值沿加密和解密方向分别以概率1取值为0和1时,则找到了一条不可能差分特征,这种产生矛盾的情况被称为miss-in-the-middle.2017年欧密会上Sasaki和Todo给出了利用MILP(mixed-integer linear programming)自动化搜索不可能差分特征的方法[24],然而由于全空间搜索的复杂度过高,该方法也需要限制输入和输出差分均只有1比特或1个S盒活跃.SIMON算法由于采用线性密钥扩展算法,其每一轮的差分活跃比特数并不随着轮数的增加而逐渐增加,限制其输入输出差分和主密钥差分中活跃比特数并不能得到更长轮的不可能差分特征.

本文通过对SIMON加密算法中间轮某1比特差分取确定值时,每一轮差分需满足约束条件的研究,得到其子密钥差分需满足的约束条件,并结合密钥扩展算法的MILP模型进行求解,如果有解则说明找到了一条不可能差分路径,如果模型无解则需要继续调整约束条件求解.

本文第2节给出SIMON算法和MILP模型的基本介绍,第3节研究了SIMON子密钥需满足的约束条件.本文首次给出SIMON32/64和SIMON48/96的相关密钥不可能差分特征,分别为13轮,其对应的单密钥下最长不可能差分特征分别为11轮和12轮.第4节给出这两条不可能差分特征矛盾产生的具体推导.

表1SIMON32/64和SIMON48/96不同类型区分器比较

Table 1 Comparision of different distinguishers for SIMON32/64 and SIMON48/96

分析方法 SIMON32/64 SIMON48/96概率 轮数 来源 概率 轮数 来源差分路径 2−30 11 [5] 2−46 15 [5]差分区分器 2−30.76 14 [5] 2−46.32 17 [3]线性路径 2−30 11 [25] 2−46 15 [25]线性区分器 2−29.43 13 [25] 2−46.3 21 [25]积分区分器 1 15 [11] 1 16 [17]相关密钥差分路径 2−24 15 [19] 2−36 15 [19]零相关线性特征 1 11 [11] 1 12 [11]不可能差分特征 1 11 [19] 1 12 [19]相关密钥不可能差分特征 1 13 本文 1 13 本文

2 预备知识

2.1 符号

本文中用到的符号如表2所示.

表2 符号Table 2 Notations

2.2 SIMON算法描述

SIMON算法是一种Feistel类型算法,其轮函数仅包含:与运算、循环移位运算和异或运算,因此具有非常好的软硬件实现性能.SIMON算法依据不同参数一般记为SIMON2n/mn,分组长度记为2n,其中n∈{16,24,32,48,64},密钥长度记为mn,m∈{2,3,4},其对应加密轮数如表3所示.其轮函数为F(X r,X r−1)=(S a(X r)⊙S b(X r)⊕S c(X r)⊕X r−1⊕K,X r),循环移位参数(a,b,c)取值为(8,1,2),轮函数示意图如图1所示.

图1 SIMON轮函数Figure 1 Round function of SIMON

表3 SIMON参数Table 3 SIMON parameters

SIMON算法密钥扩展算法根据m取值不同分为3个版本,但均为线性扩展算法,如下所示

其中常数C=2n−4=0xff···fc,常数序列{z j}的生成详细过程见文献[1],由于本文只考虑子密钥差分,而轮常数不影响差分所以本文不再赘述.

2.3 MILP模型介绍

混合整数线性规划(MILP)的方法在分组密码的安全性分析中发挥了重要作用.2014年亚密会上Sun等人首次给出构造分组密码算法MILP模型的方法[26],对多种算法的最小活跃S盒路径和高概率差分路径、线性路径的搜索效率都很高,利用MILP更新了多种算法的最优路径及其包含的轮数.2017年欧密会Sasaki和Todo给出了利用MILP模型自动化搜索输入输出差分只有1比特或1个S盒活跃的不可能差分特征的方法[24].2016年亚密会Xiang等人给出了利用MILP模型自动化搜索基于可分性的积分路径的方法[17].目前MILP已成为分组密码算法安全分析必不可少的重要工具,需要解决的关键问题是如何构造适合不同分析方法和加密算法的MILP模型.

由于本文目标是搜索SIMON相关密钥下不可能差分特征,只需构造并求解密钥扩展算法的MILP模型和附加的约束条件,而SIMON算法采用线性的密钥扩展算法,只包含异或操作,所以在该部分我们只展示能够完整描述异或操作的线性不等式组.SIMON算法不同密钥长度对应的密钥扩展算法中子密钥差分需满足的条件如下:

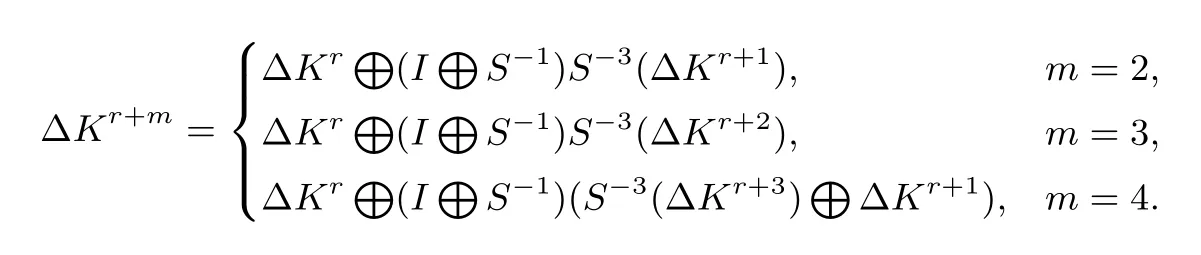
以m=4为例,第r轮子密钥的第i比特差分满足等式

Sun等人在文献[24]中给出的刻画异或操作的约束条件需要引入虚拟变量.设a⊕b=c,其对应的线性不等式组为

3 SIMON不可能差分特征的约束条件

对SIMON算法搜索不可能差分特征,无论是手动推导概率为1的截断差分特征还是用MILP等自动化搜索工具,都需要限制输入输出差分只有1比特活跃,这么做的依据是差分活跃比特数会随着轮数增加而逐渐增多.以1比特活跃作为初始值期望其截断差分路径能够包含尽可能多的轮数,而SIMON密钥扩展算法采用线性结构,即使限制主密钥差分只有1比特活跃,也会在几轮之后很快完成全扩散,这使得无法通过限制初始活跃比特数的方法来得到相关密钥下最长不可能差分特征.本文在3.1节中研究了SIMON中某一比特位置差分取确定值时,其上一轮差分需满足的必要条件,并在3.2节中首次给出不限制初始差分值的截断差分路径,与原有结果进行对比,以SIMON32为例利用miss-in-the-middle方法,使截断差分在中间轮某比特位分别以概率1取值为0和1产生矛盾,在3.3节中给出此条件下每一轮子密钥需满足的约束条件.

3.1 ROTATION-AND运算差分传播性质

3.2 SIMON32截断差分

SIMON算法截断差分已有结果都是限制输入差分只有1比特取值为1,其他位置差分取值均为0,以SIMON32为例,结果如表4所示.

表4 SIMON32输入差分只有1比特活跃的截断差分路径Table 4 Truncated differential trails for SIMON32 with 1-bit constraint

利用3.1节中定理1,我们先确定中间某一轮第i比特位差分取值为0,不妨取i=1.由此逆向推导当已知第6轮截断差分(????????????????,?0??????????????)以概率为1成立时,第0-5轮所需满足的约束条件,结果如表5所示.

表5 SIMON32第6轮右半部分第1比特位以概率1取值为0时需满足的约束条件Table 5 Constraints for value of 1th bit of 6th round of right block of SIMON32 with probability 1

3.3 SIMON32子密钥差分约束条件

本节以SIMON32为例,构造出其中间轮能够以概率为1产生矛盾时其子密钥差分需满足的约束条件.根据3.2节中给出的当中间第r轮第i比特差分以概率1取值为0或1时,其他轮差分必须满足的差分约束条件,结合引理1推出轮子密钥差分必须满足的约束条件.分为如下两步:

由此随着轮数的增加和取确定差分值的比特数的增加,所有可能的情况数量会呈指数增长.由于当前计算能力有限,本文增加了一条限制条件:轮子密钥差分约束条件中只有一比特差分值被限制为1,且该限制条件发生在第2步中.即若需保证中间轮某位置差分值取0时,其前几轮差分取值情况均参照式(4),若需保证中间轮某位置差分值取1时,其前几轮约束条件中只有1比特约束条件参照式(7),其他比特位约束条件均参照式(6).满足约束条件式(7)的比特位是可以选择的,由此轮子密钥差分存在多组可用约束条件,结合密钥扩展算法MILP模型依次对其进行求解,若有解则得到一条相关密钥不可能差分路径.

表6 SIMON32相关密钥不可能差分中子密钥差分的一组约束条件Table 6 Constraints of subkey difference for related-key impossible differentials for SIMON32/64

4 SIMON32和SIMON48相关密钥不可能差分特征

本节给出对SIMON算法搜索相关密钥不可能差分特征的步骤,并在图2中给出SIMON32/64的一条13轮相关密钥不可能差分路径(0000,2a94)↛(c4e9,0000),其主密钥差分为(2a94,8000,4082,8005),在图3中给出SIMON48/96的一条13轮相关密钥不可能差分特征(000000,e14102)↛(18852e,000000),其主密钥差分为(e14102,000000,000002,0000cc),从而显示的展示中间轮矛盾产生原因.图2和图3分别用蓝色标记出为满足中间轮0-1矛盾以概率1发生时其每一轮差分和子密钥约束条件中必须取固定值的差分比特位,用红色标记出子密钥约束条件中唯一差分值被限制为1的比特位,其中图2可以和表6对应.

图3 SIMON48/96的13轮相关密钥不可能差分路径Figure 3 13-round related-key impossible differential trail for SIMON48/96

SIMON算法相关密钥不可能差分特征搜索步骤如下:

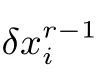
(3)结合2.3节MILP模型中异或操作对应的线性不等式组和SIMON算法的密钥扩展算法,得出其MILP模型,并在此基础上添加以上2步得到的约束条件,利用Gurobi求解工具(https://www.gurobi.com)对该模型自动化求解.若有解,则得到一条相关密钥不可能差分特征,将子密钥差分结果代入得到完整路径,例如图2和3;若无解,去掉首轮或最后一轮约束条件后继续求解,直到包含轮数小于等于单密钥下不可能差分特征轮数为止,若仍无解则回到第2步调整子密钥差分约束条件中差分值为1的比特位后继续求解.

图2 SIMON32/64的13轮相关密钥不可能差分路径Figure 2 13-round related-key impossible differential trail for SIMON32/64

5 总结

目前对于分组密码算法单密钥下不可能差分特征的搜索结果有很多,无论是对基于字运算还是基于比特运算的算法,考虑到算法本身的扩散性,一般化方法是限制其输入和输出差分均只有一个S盒活跃或只有一比特活跃作为初始搜索条件,并结合其概率为一的截断差分路径找出符合miss-in-the-middle条件的路径.随着分组密码算法中自动化搜索算法的广泛应用,利用算法MILP模型并给定输入输出差分即可自动化检测该路径是否为不可能的.但由于基于比特运算的分组密码算法全空间检测复杂度过高为O(22n),其中n为分组长度,目前不可能差分路径自动化搜索仍保持输入输出差分只有一比特活跃的限制.若密钥扩展算法是随着轮数增加而逐渐扩散则可以沿用此搜索策略,如文献[20]中利用MILP对SIMECK算法搜索输入输出差分在1比特限制条件下的最长轮相关密钥不可能差分特征.而对于SIMON算法我们沿用此搜索策略,对SIMON32只能找到最长11轮相关密钥不可能差分特征,此轮数与单密钥下最优结果保持一致.其原因是由于SIMON采用了和SIMECK完全不同的线性密钥扩展算法,其活跃比特数并不随轮数增加而逐渐扩散,难以直接控制其每一轮子密钥差分.

那么SIMON算法在相关密钥条件下是否存在包含更多轮数的不可能差分特征?如何在无一比特活跃限制条件,全空间搜索复杂度高达O(2(m+2)n)的情况下,对SIMON算法搜索尽可能包含更多轮数的相关密钥不可能差分特征?本文通过研究SIMON算法中非线性部件ROTATION-AND输出差分中第i比特以概率1取值为0或1时其输入差分需满足的充要条件,结合miss-in-the-middle方法,在给定中间轮某一比特差分值后,分别沿加密和解密方向以概率1扩展.最后得到当中间轮第i比特差分以概率1取某确定值时,其对应的输入或输出差分需满足的条件.考虑到每一轮子密钥均以异或的方式加入每一轮运算,在搜索相关密钥不可能差分特征时还需考虑由子密钥差分引起的混乱和扩散.本文结合截断差分约束条件不断调整子密钥差分的约束条件,使每一轮在引入子密钥差分后仍能保持中间轮第i比特以概率1取差分值0或1.通过利用MILP模型对SIMON算法密钥扩展算法和约束条件进行求解,若模型有解则得到一条相关密钥下不可能差分特征,否则需要调整子密钥差分约束条件继续求解.

利用本文方法对SIMON32/64和SIMON48/96分别得到一条13轮相关密钥不可能差分特征,而其单密钥下最长轮不可能差分特征包含轮数分别为11和12轮.这也是首次有对SIMON算法相关密钥不可能差分特征的搜索结果,是对SIMON算法相关密钥条件下安全性分析的补充.

同时本文方法也存在一些改进空间.第一,密钥扩展算法约束条件存在多比特差分为1的情况,由于搜索条件限制本文目前只考虑了1比特的情况,如果能自动化遍历所有可能的子密钥差分约束条件并求解可能会得到更多数量的或包含更多轮数的相关密钥不可能差分特征;第二,利用MILP求解约束条件的方法得到子密钥差分,对SIMON32和SIMON48求解速度是比较理想的,最多只需要几分钟,而对大于等于64的分组长度求解速度非常慢,如果能调整密钥扩展算法MILP模型或使用其他更高效的求解方法,则可以对其他参数搜索得到其相关密钥下不可能差分特征.

本文通过对SIMON相关密钥不可能差分特征的搜索,并与SIMECK算法相同条件下结果对比,发现密钥扩展算法的差分变化规律对相关密钥不可能差分特征有很大影响.若限制SIMON算法主密钥差分只有1比特活跃其余全0,无法得到比单密钥条件下包含更多轮数的不可能差分特征,而采用本文方法能够对SIMON32/64和SIMON48/96分别给出一条13轮相关密钥不可能差分特征,这也是SIMON算法不可能差分特征首次得出相关密钥条件下的搜索结果.随着计算能力的提升,SIMON和SIMECK算法相关密钥不可能差分特征的搜索还有很大的研究空间,研究结果对算法安全性研究和密钥扩展算法的设计都有很重要的意义.