2010年云南复杂山地年降水量精细化分布研究

杨鹏武 王学锋 范立张 杨晓鹏

（云南省气候中心，昆明 650034）

0 引言

精细化降水量信息对于区域水资源管理、旱涝灾害预防、环境治理等方面均具有重要意义，随着大气数值模式的不断发展，气象要素模拟方面取得了长足的进展，但由于降水产生的内部机理尚不完全明确，准确模拟区域降水较为困难，对于复杂下垫面更难以实现。近年来，气象部门加大了区域气象站的建设，已具备一定规模，通过一些技术处理，可以获得较高精度的区域雨量分布。降水随时空而变化，主要依赖于大气、地理、地形等多种因素，而仅考虑地理地形影响下的降水，反映的是降水量分布的一种准常态，对分析月、年、年际等较长时间尺度的降水量分布比较适合。不少学者建立降水与地理地形因子间的关系，推算降水量的空间分布及变化，如Ollinger等建立了北美地区降水等气象要素与地理位置、地形高程等的回归模型；黄炜等建立了年、季降水量和地理、地形因子（包括纬度、经度、地形高程、坡度、坡向和遮蔽度）的关系模型。

通常估算降水量空间分布的方法有3种：整体法、空间局部插值法和混合法。整体法是用数学表达式来描述降水量与影响因子之间关系的一种估算方法，包括趋势面法、多元回归法等，如Cross等运用多元回归法建立了菲律宾气温和降水回归模型，提高了血吸虫病发生气象条件的预测精度；空间局部插值法是仅仅用临近点的降水数据来估计未知点的降水值，包括泰森多边形法、反距离权重法（IDW）、克里金法（Kriging）等，庄立伟等比较了东北日降水的空间插值方法，认为IDW方法优于克里金法；混合法是在整体法估算空间降水的基础上，用空间局部插值法对残差值进行局部插值，该方法可以有效提高估算度。Vicente-Serrano等用多种插值方法对西班牙埃布罗河谷地的降水进行估算，经过对比，发现用多元回归法结合克里金插值的混合法估算的区域降水效果最理想。

虽然以上3种方法在估算降水量空间分布方面得到了广泛的应用，但各有不足，其中，整体法虽然考虑了降水的影响因子，但由于将整个分析区域考虑为一个单一类型，在研究范围较小时效果较好，但对较大范围的降水空间分布却难以给出准确的估算；局部插值方法是仅通过邻近测点降水信息、空间相关等来估计待插点的降水量，由于较少考虑降水影响因子，插值效果往往不理想；混合法虽然是整体插值法与局部插值法的结合，但是仍然以整体插值法为基础，并没有解决将所有站点仅划为一个单一降水类型的局限。

通过分析以上3种插值方法的不足，并针对云南山高谷深、降水差异大的特点，本文提出一套以气象站数据为基础，结合格点地形数据，应用主成分分析、聚类分析、判别分析及混合插值法（多元线性拟合结合空间局部插值法）来推算云南年降水量精细化（1 km×1 km格点）空间分布的方法。

1 资料及方法

1.1 资料选取

1）站点资料：为了检验上述方法的适应性，本文选取云南一个典型干旱年份2010年进行分析，并通过分析结果了解当年降水的空间分布，资料为经过质控的125个国家气象站及1055个区域气象站逐时降水资料及各站点的经度、纬度、海拔高度资料。

2）数字高程资料（DEM）：为了获取云南各气象站的坡度、坡向数据及全省1 km×1 km格点地理、地形数据（经度、纬度、海拔、坡度、坡向），本研究使用了由美德联合研制的约90 m分辨率SRTM V4.1 DEM数据，其中气象站的坡度、坡向直接由90 m分辨率DEM计算得出，1 km×1 km格点地理、地形数据是通过对90 m分辨率DEM重新采样后计算获得，图1为基于DEM的云南地形图。

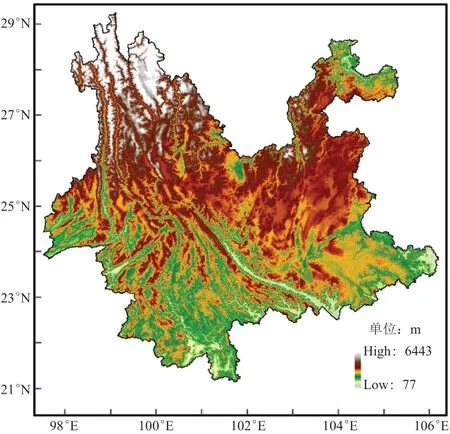
图1 云南地形图Fig.1 Yunnan topographic map

1.2 技术方法

采用主成分分析（PCA）、K-means聚类分析、多元线性拟合、朴素贝叶斯分类、Kriging插值、IDW插值等方法对2010年云南年降水量空间精细化（1 km×1 km格点）分布进行研究，并通过K-fold交叉验证法、相关系数（

r

）、平均相对误差（MRE）等方法进行结果验证。其中K-means聚类法的关键是确定聚类数，通常根据聚类有效性指标来判断不同聚类数的聚类效果，常用的聚类有效性的评价指标有： Calinski-Harabasz（CH）指标、Davies-Bouldin（DB）指标、Silhouette（S）指标[23-24]。

2 气象站年降水量分析

2.1 多重相关性分析

本文研究的是年降水量的空间分布，由于时间尺度较大（准常态），如前言所述，仅考虑地理、地形因子便可以较好地反映年降水量分布特征，本文选取的地理、地形因子（以下简称因子）分别为经度（

λ

）、纬度（

φ

）、高程（

h

）、坡度（

α

）和坡向（

β

），由于原始因子之间往往存在较强的相关性，所代表的信息相互重叠，直接应用常常会增大模型误差、破坏模型稳定性。因此，在应用之前需要对因子进行多重相关性分析。表1 给出了因子之间及与2010年降水量的相关系数（

r

），从表中可以看出：

r

(

φ

,

h

)接近0.5，说明云南气象站的纬度和海拔具有较高的线性关系，这主要因为云南地形呈东南低、西北高分布，与纬度的南北分布比较相近所致。为了消除因子之间的高线性，简单的处理就是删除那个与年降水量相关性不显著的因子，但从

r

(

φ

,

p

)=-0.30、

r

(

h

,

p

)= -0.23（均通过了0.01的显著性检验）可以看出，无论纬度、还是海拔都与年降水有比较密切的关系，剔除哪个都是不合适的。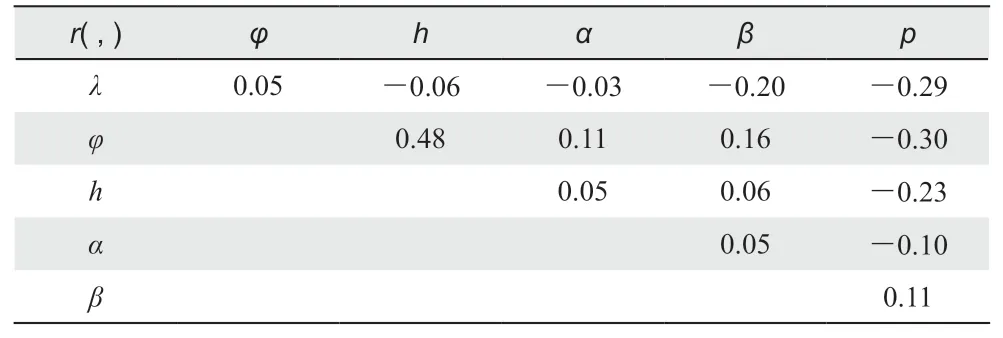

表1 自变量相关性分析Table 1 Correlation analysis of independent variable

2.2 消除因子间高相关性

PCA是目前消除因子间高相关性效果较好的方法，PCA是从原始因子中选取一个特征子集，该子集在消除相关及冗余特征的同时，具有更好的分离度。为了便于后面分析的一致性，本文将气象站因子和1 km×1 km格点因子一起进行PCA分析，将得到的特征值按从大到小排列，并计算各主成分的累积方差贡献率（图2），可以看出，第一主成分的方差贡献率已经接近50%，而前3个主成分的累积方差贡献率超过90%，说明前3个主成分已经能够较好地反映原因子的主要特征，因此，选取前3个特征值对应的特征向量生成因子主成分。通过PCA变换消除了因子之间的高相关性，然后用因子主成分直接对全省气象站年降水量进行拟合，发现拟合结果并不理想，主要原因是因为云南地理跨度较大，局部地形复杂，所有气象站仅用一个拟合方程，必然存在较大的误差，为了减少误差，对气象站点进行分类拟合是必要的。

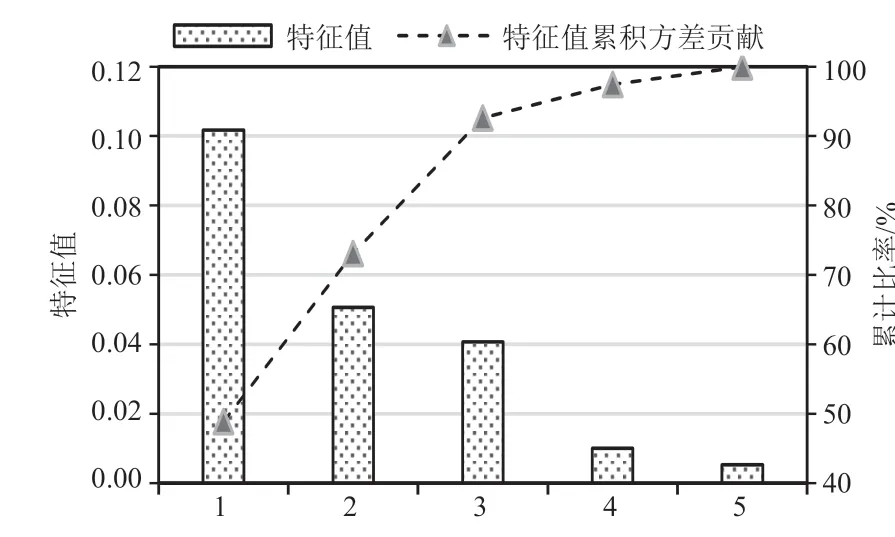
图2 主成分特征值及累计比率Fig.2 Principal component characteristic value andcumulative ratio

2.3 降水分类

聚类分析是当前研究数据分类的热门方法，而K-means是一种典型的基于欧式距离的聚类算法，该算法认为两个对象的距离越小，相似度越大；距离越大，相似度就越小。应用K-means对气象站年降水进行分类，选择的聚类因子为：气象站年降水量及PCA生成的因子主成分。K-means的难点是确定最佳聚类数，目前通常的做法是先确定聚类数

k

的测试范围[

k

,

k

]，然后进行逐个测试，从中选取最佳聚类数。其中，下限

k

一般从2开始，但考虑到云南省较大的地理跨度及复杂的下垫面分布，较少的分类无法反应年降水量的真实特征，因此本文将下限

k

设定为4。上限

k

通过经验公式

k

≤来确定，其中

n

为气象站数。通过计算，本研究的聚类数测试范围为，对测试范围的不同聚类数进行K-means分析，然后通过

DB

、

S

和

CH

这3个指标检验聚类效果，结果发现，

S

、

CH

指标均在聚类数为5时，达到了最优值，而

DB

指标在聚类数为4时聚类效果最佳，为5时次之。

绘制聚类数为5时的2010年气象站年降水分类图（图3），图中1～5类不仅体现了各气象站局部地理、地形差异，更主要体现了降水量从少到多的分布，图中可以看出，既可以明显区分哀牢山以东、以西两侧作为西南暖湿气流迎风坡和背风坡的降水类型差异，也可以识别出西部、南部边缘地带的多雨形态，同时，各个类型的样本数比较均匀（最多、最少类型占气象站比例分别为：25.5%、15.3%），可以有效避免多项式拟合时出现过拟合或者欠拟合现象。因此，将云南省2010年降水分为5类是比较合理的。

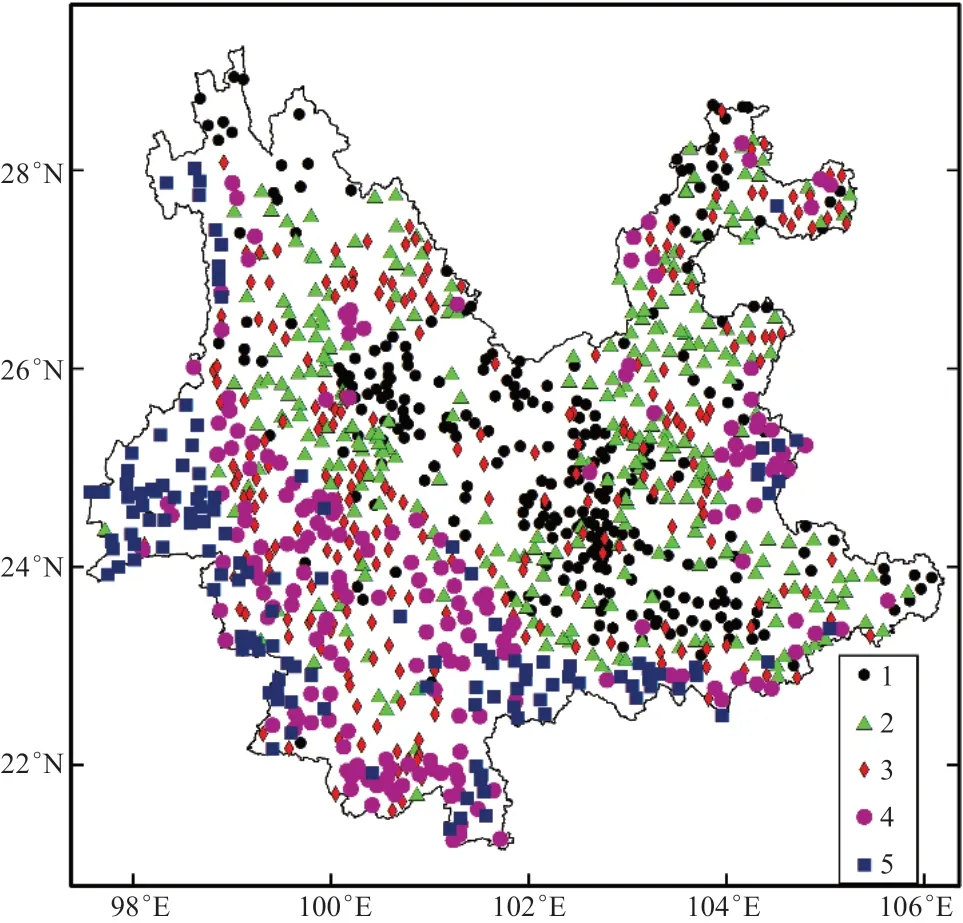
图3 聚类数为5时的2010年气象站降水分类图Fig.3 Clustering map of weather stations in 2010 whenthe clustering number is 5

2.4 回归方程拟合

聚类完成后，便可以针对每种降水类型拟合多元线性回归方程。方法是：每种类型都随机选取80%的站点作为建模数据，其余20%数据用作效果检验。所有拟合方程均通过了0.01的显著性

F

检验，说明方程的拟合是有效的，同时，检验数据的实测值与拟合值的

r

值均在0.44以上，且MRE值均小于0.30，说明方程的泛化能力比较令人满意。

3 格点年降水量分析

3.1 格点归类

为了计算云南格点年降水量分布，首先需要将全省所有格点归类到2.3节生成的不同降水类型中，然后通过各类型的回归方程计算格点年降水量。朴素贝叶斯法（BC）是大数据分析中较为常用的归类方法，该方法逻辑简单、易于实现。应用BC归类，首先需要建立BC模型，即在训练集合上得到建模各要素的先检概率，本文建模要素为气象站的因子主成分及所属类别（用1～5表示）。为了构建最合适的模型，本文采用K-fold交叉验证法（记为K-CV）进行模型构建，该方法将全省气象站点随机均分成K组，将每组的数据分别充当一次验证数据集，其余的K-1组的数据集作为训练数据集，K-CV可以有效地避免过学习、欠学习的状态发生。本文取

K

=10，通过K-CV法训练BC模型，

结果表明平均判错站数为5，占检验站点比率为0.42%，最差组的判错站数为8，占检验站点比率为0.68%，最好组的判错站数为1，占检验站点比率仅为0.08%。从分析可以得到，无论哪个分组都有很好的判别能力，本文选择出错率最小的第2组进行建模，然后对各格点进行归类。

3.2 格点年降水量推算

对归类的各格点分别应用第2.4节生成的拟合方程进行格点年降水量拟合，生成全省2010年格点降水量分布图（图4），从图中可以清晰地分辨出哀牢山以西的多雨区和以东的少雨区，但是由于拟合值趋于平滑（主要集中在600～1200 mm），对局地降水特点表现不足，同时不同降水量级的区域比较规则，与实际有一定差别，因此需要进一步订正。

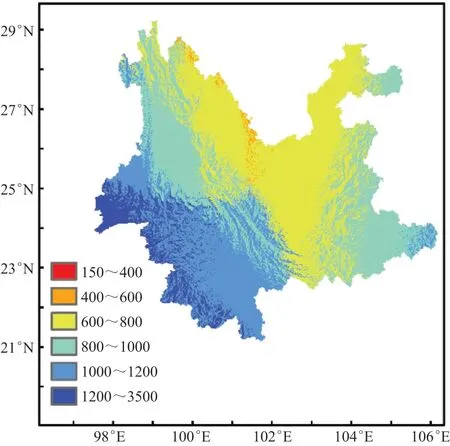
图4 云南2010年降水量拟合图（单位：mm）Fig.4 Fitting diagram of precipitation in Yunnan in 2010(unit: mm)

3.3 格点年降水量订正

用观测值减去拟合值即为残差（

ε

），年降水量残差可以看作是局地的气候效应。为了提高格点年降水量的估算精度，本文尝试对站点年降水量

ε

进行空间插值，获得全省各格点处的

ε

值，然后把

ε

值与第3.2节生成的格点拟合值相加，生成格点年降水量订正值。目前，克里金插值法（Griging） 和IDW法是常见的两种空间插值方法，为了检验两种插值方法对云南年降水量的订正效果，本文随机选取80%的气象站进行全省年降水量

ε

空间插值，然后将插值结果与所有气象站年降水量拟合值相加，生成气象站年降水量订正值，再用另外20%的气象站对订正值进行检验。检验站点年降水量观测值振幅较大，而拟合值比较平缓，与观测值有一定的差别（MRE为0.25），通过IDW和Griging订正后的年降水量振幅明显增大，与观测值比较贴合（MRE值分别0.17、0.19），说明订正方法有效。由于IDW方法得到的MRE更小，因此，本文选择IDW作为年降水量

ε

的插值方法。订正后的云南省2010年1 km×1 km格点降水量分布图（图5），不仅克服了拟合图中不同降水量级的区域比较规则的问题，而且格点极值与站点实测极值也比较接近（格点年降水量最大值、最小值分别为：3037，153 mm；气象站分别为：2933，185 mm），同时也可以看出，2010年云南年降水分布非常不均，滇中及以南以西、滇西北北部的大部分区域降水量明显较少，多不足800 mm，而滇西、滇南的边缘区域降水量比较丰沛，多超过1200 mm，其他区域降水多处于800～1200 mm。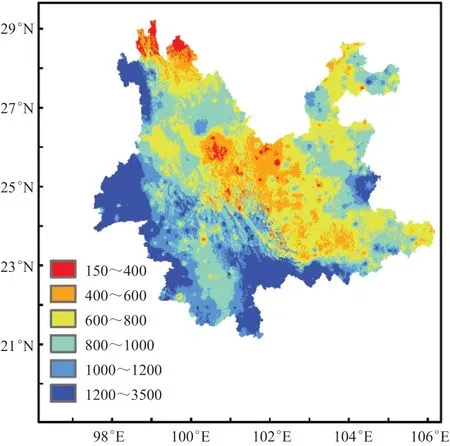

图5 云南2010年降水量订正图（单位：mm）Fig.5 Revised precipitation figure of Yunnan in 2010 (unit: mm)

4 结论与讨论

本文通过以上的分析及验证，可以获得以下结论。

1）气象模型所用的原始因子间往往存在多重相关性，会导致模型不稳定、泛化能力差。PCA方法不仅可以降维去噪，生成的新因子互不相关，同时还尽可能地保持了原有因子的信息，是消除因子间多重相关性的一种较好方法。

2）利用K-means方法对站点年降水类型进行聚类分析，不仅区分出哀牢山东、西两侧作为西南暖湿气流迎风坡和背风坡的降水类型差异，也识别出西部、南部边缘地带的多雨形态，得到了比较理想的分类结果，说明K-means方法在复杂山地降水分类方面具有较好的适应性。

3）在站点降水类型聚类的基础上，利用朴素贝叶斯分类法对格点降水类型进行归类，朴素贝叶斯分类法虽然算法简单，但是如果所选因子与降水量的关系比较强，同时因子之间独立性较强，分类效果会非常理想，因此朴素贝叶斯分类法是处理气象信息分类的一个简洁而又准确的分析方法。

4）基于聚类之上的混合插值法，是对传统混合法插值的发展，即结合了传统混合插值法对局部地形影响地勾画，又很好地与聚类方法相结合，对研究复杂地形下气象因子精细化分布具有很好的应用前景。

5） 分析中还存在一些问题，即陡峭地形下的实测降水值与拟合值仍存在较大的差异，主要原因是复杂地形观测站点仍然较少，无法更精细地刻画地形对降水的影响所致，相信随着今后气象站点的不断加密，会有所改进。