基于SVD与最小化互相干系数的测量矩阵优化方法
2021-11-19张瑞孟晨王成王强
张瑞,孟晨,王成,王强
(陆军工程大学石家庄校区,河北石家庄,050003)
0 引言
压缩感知[1](compressive sensing,CS)的理论是由Donoho等人在2006年提出的。压缩传感的主要思想是将信号采样和信号压缩结合起来,前提是原始信号是稀疏的或可以被稀疏地表示。压缩采样通过减少信号尺寸来完成压缩,而不需要奈奎斯特采样的中间阶段。通过相应的信号重建算法,用比奈奎斯特采样更少的采样数直接重建原始信号,从而节省了传输和存储成本,降低了计算复杂性和能耗。由于压缩感知可以用比Nyquist要求更低的频率对信号进行采样,压缩感知提高了信号的可压缩性和可恢复性。这些特性使得CS在信号处理的许多领域有广泛的应用。一些典型的基于CS的应用包括单像素成像[2],图像和视频的恢复[3],无线图像传感器网络[4],以及一些生物医学信号处理领域,如核磁共振成像[5](MRI)和心电图(ECG)信号处理[6]。
原始信号的稀疏表示、测量矩阵的设计和信号重构算法是CS理论的三个主要部分。压缩感知过程如图1所示。
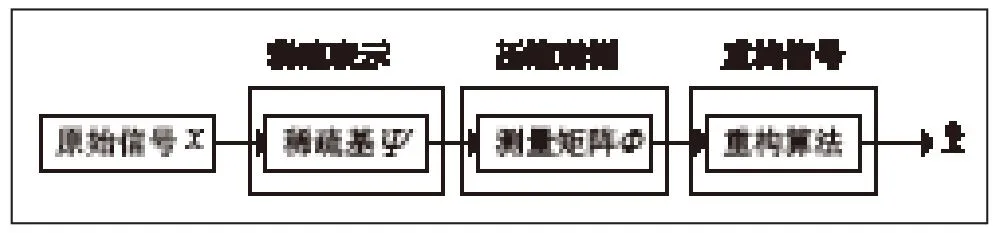
图1 压缩感知过程
测量矩阵作为CS理论的关键研究内容之一,它的设计与选择将直接影响到信号压缩感知的效果。
基于此,本文在压缩理论的框架下,针对现有测量矩阵提出了一种新的优化方法,进一步提升信号压缩测量的性能。本文首先利用奇异值分解,优化初始测量矩阵的非零奇异值,然后借鉴了最小化互相干系数的思想,对得到的测量矩阵进行了进一步的优化。
1 测量矩阵设计
从以上对CS的理论介绍可以看出,测量矩阵的性能直接影响信号重构的结果,而测量矩阵是信号稀疏和信号重构之间的重要中间环节。Candès为压缩感知理论做出了开创性的工作。文献[7]证明了测量矩阵和正交稀疏基是尽可能不相干(正交)的,测量矩阵将有较大的概率具有更好的性能。
一般来说,稀疏基 是已知的且固定的,所以通过设计和优化测量矩阵,可以尽可能地减少测量矩阵和稀疏基之间的相干性。另外,直观的理解是,如果Φ和Ψ是不一致的或不相关的,从原始信号采样将包含更多的新信息,因此,测量矩阵的性能主要取决于测量矩阵和稀疏基矩阵之间的互相关性。
根据相关的数学理论,测量矩阵与稀疏矩阵之间的不相干性可以间接转化为Gram矩阵尽可能接近单位矩阵的问题。Gram矩阵定义如下:

非相干性表示测量矩阵与稀疏矩阵之间的正交性质。根据Gram矩阵的定义,最小化Φ和Ψ之间的互相干性,相当于最小化相应的Gram矩阵中的非对角元素的绝对值,使Gram矩阵尽可能接近单位矩阵。Gram矩阵越接近单位矩阵,Φ与Ψ之间的相互相干越小。因此,构造更好的测量矩阵相当于解决以下优化问题:
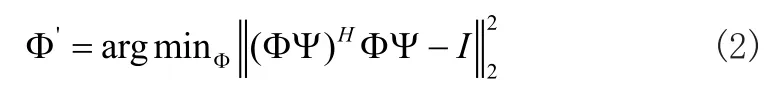
其中I是N×N维的单位阵。因此,最小化式(2)可以有效地减小互相关性。
2 基于SVD与最小化互相关系数的测量矩阵优化方法
文献[8]指出,测量矩阵的列向量应具有良好的线性非相关性,这与测量矩阵的最小奇异值密切相关。矩阵的最小奇异值越小,矩阵的线性相关性就越大,即其独立性越弱。因此,应该增大矩阵的奇异值来提高测量矩阵各列向量之间独立性。
2.1 测量矩阵优化设计
奇异值分解(Singular Value Decomposition)是线性代数中一种重要的矩阵分解,奇异值分解是特征分解在任意矩阵上的推广。在信号处理、统计学等领域有重要应用。
本文首先对初始测量矩阵 Φ∈ RM×N(M < N)进行奇异值分解,得到:

其中D是M×N 维的半正定矩阵,U和V分别为M×M、N×N 维的酉矩阵。
然后利用Σ',构造新的测量矩阵Φ1为,
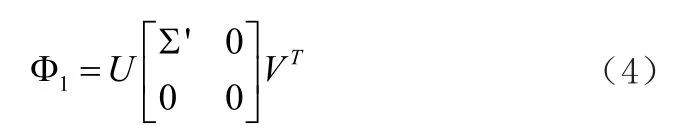
测量矩阵Φ1的奇异值得到增大,矩阵各列之间的独立性得到了提高。
考虑到Φ1仍有进一步优化的空间,本文借鉴最小化互相干系数思想对Φ1进一步优化,得到更好的测量矩阵。

降低列向量之间的互相干系数就可以转换成最小化Gram矩阵的非对角元素。其中互相干系数存在着一个下界(Welch界)[9],让测量矩阵与稀疏基矩阵的互相干系数逼近Welch界,可以保证测量矩阵具有更好的压缩观测性能。Welch界定义如下:

定义优化的目标函数为:
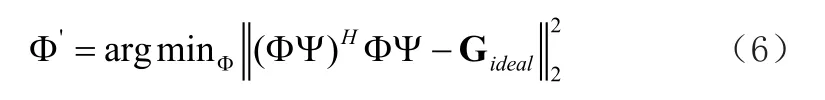
其中Gideal为重新定义的目标矩阵,满足的条件如下:
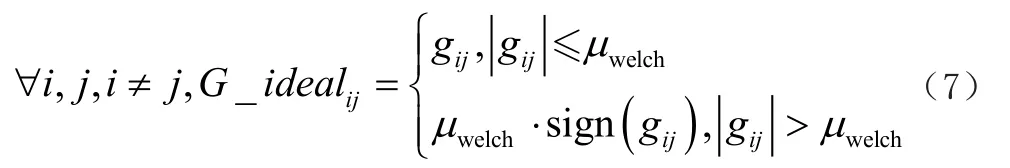
通过最小化目标函数,最后得到最优的测量矩阵Φ'。
2.2 算法实现步骤
本文提出的优化测量矩阵的算法(SVD-MCM)步骤如下:

本文算法(SVD-MCM)输入:测量矩阵Φ,稀疏基Ψ;输出:优化后的测量矩阵Φ';Step 1 对Φ进行奇异值分解,Φ=UD VT Step 2 对奇异值进行优化处理,构造新的测量矩阵Φ1 Step 3矩阵;Step 4 利用式(15)更新目标矩阵G Θ= Φ Ψ 1列归一化后得到^Θ,计算Φ1的Gram ideal Step 5 据式(14)目标函数,迭代优化Step 6 判断是否满足迭代终止条件,满足则进入Step 7则,返回Step 4 Step 7利用式(11),输出化后的测量矩阵Φ'。
3 仿真实验与分析
本实验在Matlab平台对算法进行数值仿真实验,根据压缩感知理论,高斯随机矩阵与伯努利随机矩阵具有较好的随机性,可以以较高的概率满足RIP条件,本文以这两种测量矩阵为对象,研究SVD-MCM算法对测量矩阵的优化效果。
第一组实验是压缩感知重构实验,用于比较SVD-MCM算法对信号压缩感知重构效果的影响。仿真信号选用时域稀疏信号,测量矩阵选择高斯随机矩阵,此时稀疏基为标准正交基。参数设置如下,信号长度N=256,信号稀疏度K=40,测量数目M=128。重构算法采用常用的正交匹配追踪(OMP)算法,为进一步评价重构效果,引入衡量重构性能的指标均方误差 MSE(mean square distortion):

采用本文算法优化的高斯随机矩阵(Gauss+SVD-MCM)、未经优化的原始高斯随机矩阵(Gauss+Origin)两种测量矩阵重构效果图如图2所示。
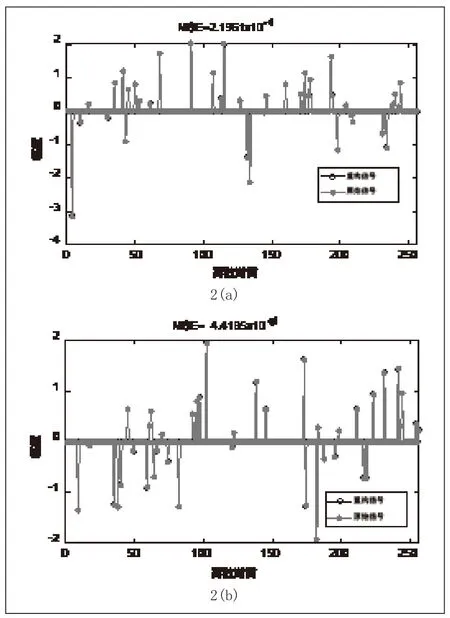
图2 重构效果:(a)Gauss+Origin;(b)Gauss+SVD-MCM。
从重构效果图可以看出,观测数目M=128时,两种测量矩阵均实现了对原信号的有效重构。对比均方误差来看,经本文算法优化后的测量矩阵,重构误差明显低于未优化的高斯随机矩阵。
实验二,设定不同的稀疏度K,比较测量矩阵对稀疏度不同的稀疏信号的重构效果。稀疏度K从10变化到80,变化步长为5。六种测量矩阵分别为原始高斯随机矩阵(Gauss+Origin)、经奇异值分解优化的高斯随机矩阵(Gauss+SVD)、经本文算法优化的高斯随机矩阵(Gauss+SVDMCM)、原始伯努利随机矩阵(Berno+Origin)、经奇异值分解优化的伯努利随机矩阵(Berno+SVD)、经本文算法优化的伯努利随机矩阵(Berno+SVD-MCM)。
当均方误差小于10-4时,则认为信号重构成功;否则,失败。统计200次蒙特卡洛实验的重构概率。
图3 为六种测量矩阵信号重构均方误差随信号稀疏度的变化关系,可以看出在其他条件不变的情况下,随着信号稀疏度的增加,信号的重构误差会增大。同时实验结果表明,高斯随机矩阵的性能要优于伯努利随机矩阵的性能。经本文算法优化后的测量矩阵性能优于奇异值分解优化方法,与原始测量矩阵相比,重构精度得到提高,重构性能明显提升。

图3 重构均方误差随信号稀疏度的变化关系
图4 为六种测量矩阵重构成功概率随信号稀疏度的变化关系。可以看出,随着信号稀疏度的增加信号的稀疏性变差,重构概率降低,经本文算法优化的测量矩阵在稀疏性较差时也可以获得较高的重构成功概率,重构性能得到了显著的改善。

图4 重构成功概率随信号稀疏度的变化关系
4 结论
本文在压缩感知理论框架下对已有的压缩感知测量矩阵优化算法进行进一步的优化,提出了一种基于奇异值分解与互相干系数最小化相结合的优化方法,保证了测量矩阵在优化后具有良好的独立性,以及与稀疏基矩阵的不相干性。实验结果验证了算法的有效性,本文算法优化后的测量矩阵性能得到了明显的改善,重构误差得到有效降低,重构成功概率得到显著提高。
