多物理场耦合作用下地铁双块式无砟轨道道床板疲劳损伤开裂行为研究

姚光磊

(西南交通建设集团股份有限公司，650032，昆明∥高级工程师)

0 引言

双块式无砟轨道是一种纵向具有连续性的钢筋混凝土结构，在使用过程中主要承受变温荷载以及列车动荷载的双重荷载。由于混凝土结构本身抗拉强度低，在双重荷载周期性作用下，其内部拉应力极易超过其抗拉强度极限，从而产生裂纹;若不及时采取控制措施，则裂纹会扩展贯通，进而改变无砟轨道结构的受力特性，影响行车安全及道床板本身的服役性能［1］。地铁双块式无砟轨道道床板典型裂缝如图1所示。

图1 地铁双块式无砟轨道道床板典型裂缝照片Fig.1 Typical cracks in bed slab of metro double block ballastless track

目前，已有的损伤累计理论主要有4类:线性疲劳累积损伤理论，双线性疲劳累积损伤理论，非线性疲劳累积损伤理论及其他如概率疲劳损伤理论。学术界大多采用线性疲劳累积损伤理论，单独研究变温荷载或者列车动荷载所引起的双块式无砟轨道道床板损伤变化。但在实际情况下，轨道结构长期置于自然环境之中，同时承受温度场和列车激扰力场的共同作用，两者通过相互耦合作用，影响着道床板结构的疲劳服役寿命，且轨道结构开裂演变过程中存在强非线性特性。

文献［1］对于多场荷载作用下高速铁路道床板的疲劳特性，采用了线性疲劳累积损伤理论对其展开研究，并得到了诸多有意义的结论。但地铁轨道结构所处环境及列车运营模式有别于高速铁路，地铁线路多处于地下，其周围环境较为单一，昼夜温差变化较为固定，温度应力变化呈现周期性。采用混凝土损伤塑性模型能模拟周期性荷载以及动荷载等多种荷载的加载情况，且能够准确地模拟列车动荷载下道床板刚度恢复的力学行为，相较于线性疲劳损伤累积理论能够更准确地分析道床板的疲劳开裂行为。

本文在有限元软件ABAQUS中，通过混凝土损伤塑性模型，建立双块式无砟轨道道床板应力应变的有限元模型;而后考虑在温度周期性变化下，以道床板最大损伤程度作为预设条件，同时在多体动力学软件Universal Mechanism中，建立列车-轨道-路基的耦合模型，计算列车行驶过程中的扣件压力，并将其施加在ABAQUS中所建立的模型上作为列车动荷载;研究温度周期性变化及列车动荷载同时作用下双块式无砟轨道道床板内部损伤变化规律。

1 混凝土结构塑性损伤模型

本文采用有限元软件ABAQUS中的混凝土损伤塑性模型来研究地铁双块式无砟轨道道床板的力学行为，该模型是在文献［2-3］模型的基础上发展而成。该模型基于混凝土塑性变化的连续介质损伤模型，以各向同性拉伸、各向同性弹性损伤，以及压缩塑性、耦合等模式共同描述混凝土的非弹性力学行为。同时，该模型基于各向相同破坏的假设，考虑单向荷载、周期性荷载及动荷载等多种加载情况，并能模拟由混凝土拉伸压缩塑性应变导致的刚度变化以及周期性荷载下的弹性刚度变化，具有良好的收敛性。

假定混凝土道床板模型损伤后弹性模量为E，其与无损伤弹性模量E0、刚度损伤因子d间的关系为:

式(1)中，d与混凝土单轴受拉和受压时的损伤参数有关。其关系如下:

式中:

dt、dc——分别为混凝土受拉与受压时的刚度损伤因子;

st、sc——分别为混凝土受拉恢复时和受压恢复时与应力有关的的应力状态函数。

在单轴拉-压反复循环荷载作用下，混凝土刚度变化如图2所示。由图2可知，在压应力作用下，混凝土材料在其屈服应力前处于线弹性变形，AB段出现材料硬化，在B点混凝土压应力达到极限，之后开始软化;在C点开始卸载，此时引入d，混凝土刚度变化为(1－dc)E0.;随后施加反向拉力，混凝土材料应力应变关系沿DF段变化，整体处于线弹性变化阶段，混凝土刚度保持为E0;之后混凝土材料达到应力峰值点F，继续加载，混凝土出现开裂，应力应变曲线沿FH段发展，此时混凝土的卸载刚度由E0变为(1－dt)E0，;应力达到零点后，进入反向加载GI段，此时混凝土的刚度改变为(1－stdc)(1－scdt)E0。

图2 单轴拉-压反复循环荷载作用下混凝土刚度变化曲线Fig.2 Concrete stiffness curve under uniaxial tension compression cyclic loading

此外，该模型的弹塑性应力-应变关系为:

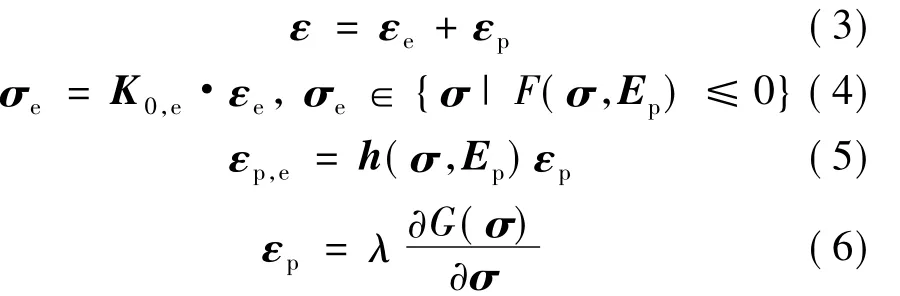
式中:

λ——非负塑性乘子;

F——屈服函数;

ε——总应变率向量;

εe——弹性应变率向量;

εp——塑性应变率向量;

Ep——等效塑性应变向量;

εp，e——等效塑性应变率向量;

σ——柯西应力矩阵;

σe——有效应力矩阵;

K0，e——初始弹性刚度矩阵;

h——权重系数矩阵;

G——流动能。

2 地铁列车-无砟轨道-路基动力学耦合模型建立与仿真计算

2.1 地铁列车-无砟轨道耦合振动模型

地铁列车模型中，每节车辆都是由车体、转向架、轮对等多个部件组成的多自由度系统。本节所建立的地铁列车-轨道-路基动力学耦合模型中，车辆考虑各个部件之间真实连接的动力学特性。各组成部件均至少考虑4个自由度，分别为沉浮、横摆、摇头、点头;车体与转向架相对于轮对需多考虑1个点头的自由度。整车模型包含4个轮对、2个转向架及1个车体，故单节车辆模型共有31个自由度。

轨道结构由钢轨、轨下扣件系统、混凝土道床板以及支承层组成，且均采用线弹性材料。其中，钢轨简化为弹性点支承的欧拉梁模型，轨下扣件系统简化为带阻尼的线弹性弹簧单元，混凝土道床板以及支承层则建立实体模型。

使用赫兹接触理论计算分析轮轨间的耦合作用力，结合前述的地铁列车-无砟轨道耦合振动模型，建立地铁列车-轨道-路基动力学耦合模型。

2.2 双块式无砟轨道-路基变温作用分析模型

在进行双块式无砟轨道结构的三维瞬态热传导分析时，其结构表面辐射利用命令SRADIAT定义。在该模型中，道床板、支承层和路基均采用DC3D8单元建立，道床板内纵向钢筋与横向钢筋采用DC1D2单元模拟。双块式无砟轨道-路基对称模型如图3所示。

图3 双块式无砟轨道-路基有限元模型Fig.3 Finite element modelof double block ballastless track subgrade

对双块式无砟轨道进行温度应力计算时，需根据热传导分析结构重新计算上述模型的应力。采用C3D8R和T3D2单元重新定义轨道结构、路基结构及钢筋;采用新的力学参数代替热力学参数，即除道床板采用损伤塑性模型外，支承层、路基及钢筋均采用线弹性模型;删除原模型中温度的边界条件，对该模型底部重新施加固定约束，两端部施加对称约束;最后再读入温度场数据。

3 计算结果分析

3.1 计算参数确定

采用文献［4］中所提出的气象和温度数据分析法，对双块式无砟轨道结构进行三维瞬态热传导分析。损伤塑性模型来源于GB 50010—2010《混凝土结构设计规范》［5］给出的本构关系。模型参数根据道床板现场浇注混凝土的标号确定。因此，道床板结构混凝土材料的刚度损伤因子dt，c计算公式如下:

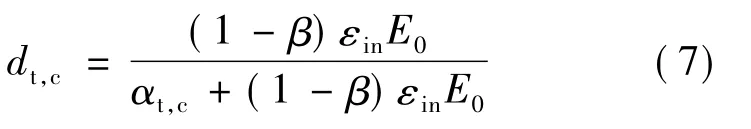
式中:

β——混凝土塑性应变与非弹性应变的比例系数，拉伸时取0.7，压缩时取0.4;

αt，c——混凝土单轴受拉应力-应变曲线下降段的参数值;

εin——混凝土非线弹性阶段的应变。

本研究中道床板结构混凝土强度等级采用C40。轨道和路基结构材料计算参数如表1～2所示。该车辆模型采用地铁B型车参数，车体轴重为14.0 t，列车运行速度为80 km/h。以地铁典型干扰轨道谱为基准［6］，经变换生成轨道随机不平顺的时域样本，将其作为轮轨系统动力分析的激励，计算各钢轨支点压力。

表1 轨道和路基结构材料参数Tab.1 Material parameters of track subgrade structure

表2 混凝土损伤塑性模型参数Tab.2 Damage parameters of concrete plastic model

3.2 温度场作用下轨道结构损伤分析

轨道结构内部初始应力对于轨道结构损伤演变规律影响十分重要。本文选取温度应力最高值，即平均最高气温时刻(14:00)作为初始温度应力计算时刻，对双块式无咋轨道结构进行受力分析和损伤变化分析，结果如图4～5所示。由图4～5可知，温度逐渐下降，道床板中拉应力随温度的下降逐渐升高;在22:00左右，轨道结构拉应力达到了混凝土拉伸强度值1.71 MPa，此时由于过大的拉应力导致道床板内部出现了细微的裂纹，有局部的损伤并使得其刚度下降;但气温仍在下降，道床板内部拉应力持续增加;在24:00达到峰值，混凝土材料出现应变软化现象，轨道结构受拉承载力下降，道床板内部损伤继续扩大。随后气温逐渐上升，道床板拉应力下降并逐渐变为压应力，但其所受损伤已不可逆，最终其损伤值保持在0.18左右。

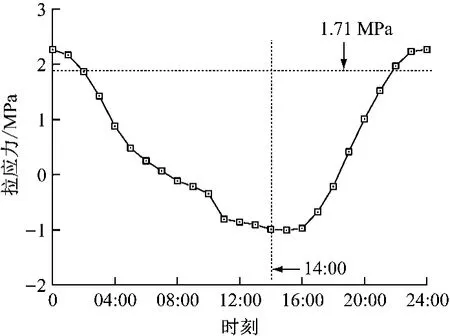
图4 温度升降过程中道床板拉应力Fig.4 Tensile stress of lower bed plate during temperature rise and fall

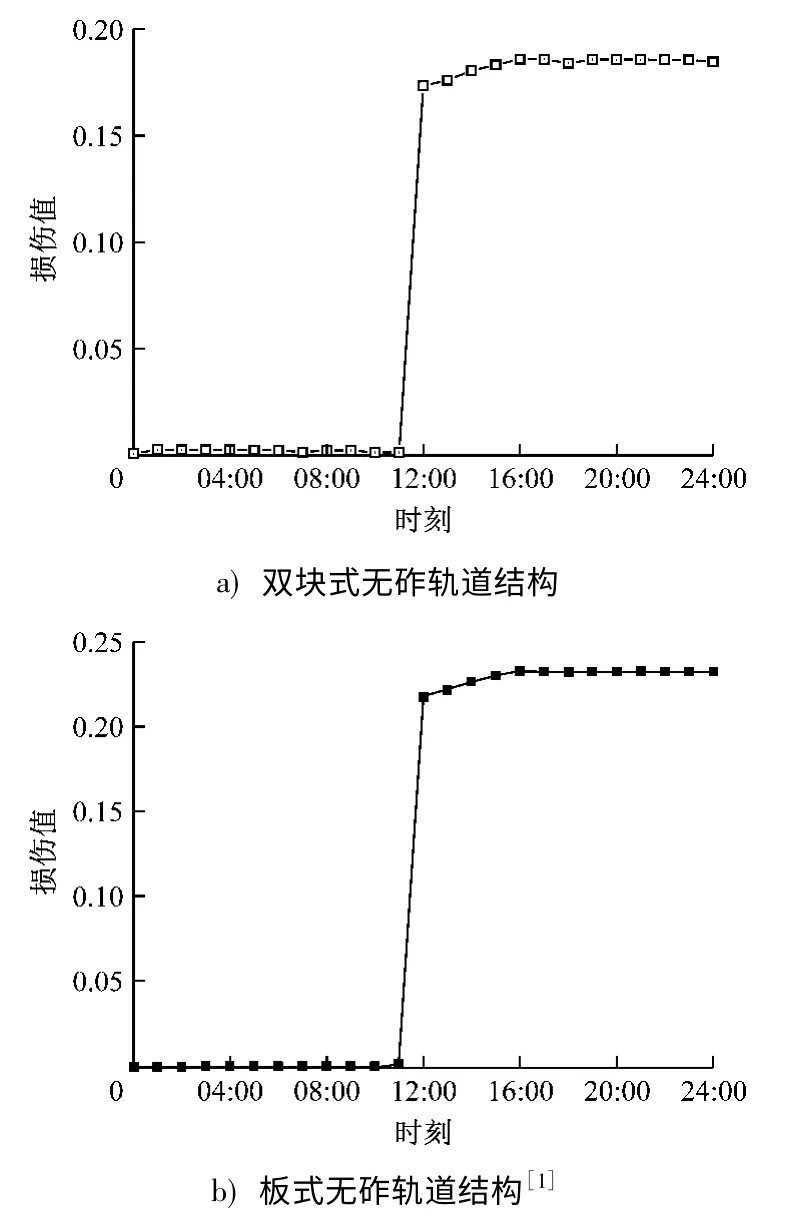
图5 温度升降过程中道床板损伤值Fig.5 Damage value of lower bed plate during temperature rise and fall

3.3 温度场与列车动荷载耦合作用下轨道结构损伤分析

由地铁列车-轨道-路基耦合动力学模型中仿真得到的道床板中部的左、右轨下支点压力，如图6所示。以道床板在周期性温度场作用下得到的最大损伤值作为分析初始值，结合前述的道床板损伤分析模型，施加图6所示的耦合模型中计算所得的钢轨各支点反力，计算车辆经过时轨道-路基结构非线性动力响应，最后得到左、右钢轨支点处道床板的损伤值，如图7所示。

图6 道床板中部左、右轨下支点反力时程曲线Fig.6 Reaction time history curve of lower fulcrum of left and right rails in the middle of track bed slab

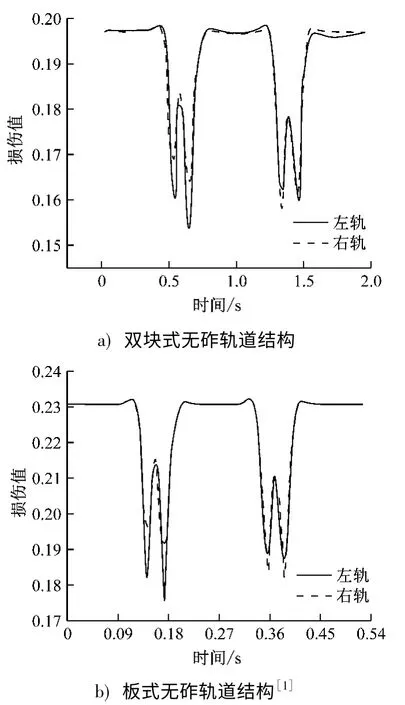
图7 道床板中部左、右轨下支点处损伤值Fig.7 Damage value of track bed plate at lower fulcrum of left and right rails

由图7可知，当列车通过道床板时，道床板刚度暂时性恢复，使得道床板损伤值短暂性下降，当列车通过后，道床板损伤值恢复稳态，保持在0.19～0.20范围内。这是由于当列车通过有损伤的道床板时，道床板内部的裂缝暂时性闭合，其刚度暂时性恢复，而在列车驶过后，其内部裂纹再度张开，这种现象被称为裂纹的“呼吸效应”。

图8为有、无损伤时轨道板位移时程曲线。由图8可知，道床板开裂后，其位移幅值会比无损伤时增大，表明随列车的周期性行驶，道床板内部的裂纹将会逐渐扩大，且最终贯通道床板。

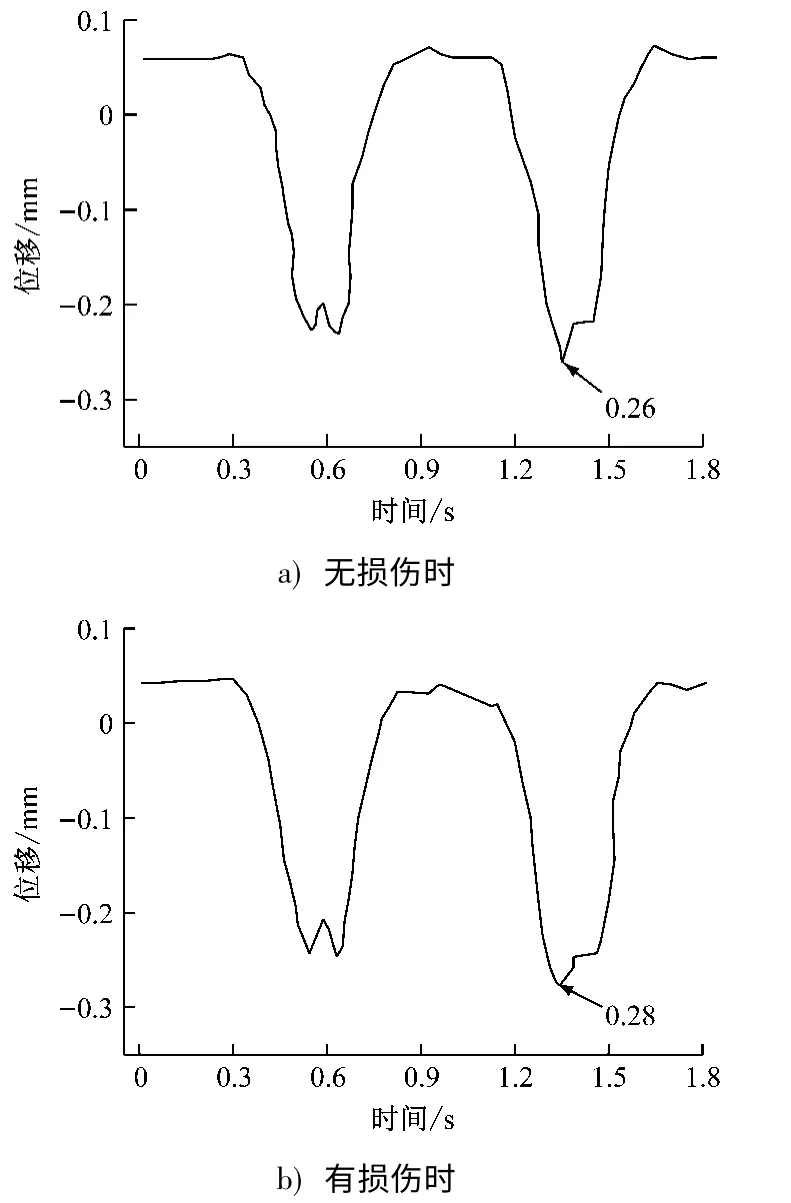
图8 有、无损伤时轨道板位移时程曲线Fig.8 Track slab displacement time history curve

综上可知，这种裂纹形成的主要原因是道床板内受温度场的作用，在板内形成很大的拉应力。双块式轨枕为预制混凝土件，其混凝土收缩变形已趋于稳定。但由于与其连接的道床板为新浇筑混凝土件，双块式轨枕内部的拉应力限制了道床板的自由收缩，使其内部产生了一定的拉应力，以及混凝土黏结面出现剪应力。当道床板拉应力或黏结面剪应力大于道床板自身的抗拉强度或道床板与双块式轨枕的黏结强度时就会产生裂纹，随后在拉应力及剪应力的共同作用下形成裂纹，在服役过程中承受的列车动荷载反复施加到道床板上，最终形成贯通的裂纹。

4 结论

1)双块式无砟轨道结构在降温过程中会沿纵向整体出现横向的弯曲变形，在低温时，道床板出现拉应力并大于其抗拉强度，内部出现裂缝，使得道床板损伤，其受拉承载力下降;在升温时，道床板内部裂缝暂时闭合，刚度暂时性恢复，但其受损已不可逆，损伤值保持在0.19左右。

2)道床板在承受周期性列车动荷载作用时，内部裂纹暂时性闭合，刚度短暂恢复，但道床板位移幅值比无损伤时增加，表明列车动荷载会加速道床板内部裂纹的扩展。

3)地铁双块式无砟轨道道床板疲劳开裂可分为2个阶段:道床板受到温度场作用，当温度下降时在板内形成很大的拉应力且在混凝土黏结面上出现剪应力，当道床板拉应力或黏结面上的剪应力大于道床板自身的抗拉强度或道床板与双块式轨枕的黏结强度时就会产生裂纹;随后道床板在拉应力及剪应力的共同作用下形成裂纹，在服役过程中承受的列车动荷载反复施加于道床板上，最终形成贯通的裂纹。