基于贝杰龙模型多点联合判断的特高压直流输电线路纵联保护
2021-11-19单节杉田鑫萃
单节杉,王 璇,田鑫萃
(昆明理工大学电力工程学院,云南 昆明 650500)
0 引 言
电流差动保护往往作为交流线路的主保护,而对于高压直流线路则往往作为后备保护。对于低电压、短线路,分布电容对差动保护动作的特性影响较小[1-2]。但对于那些有明显分布参数特性的长距离输电线路,其电流差动保护受到电容电流的影响较为严重,如果继续采用原有线路两侧的直流电流差值作为动作判据,则很难保证线路全长范围内故障下差动保护可以可靠动作[3-4]。为了克服线路分布电容电流对差动保护的影响,文献[5]分析采用π型线路模型进行电容电流的补偿,但计算误差较大,保护精度会受影响。文献[6]提出了将多种影响判据的因素统一归入分布电容参数变化,并实时在线计算分布参数数值的精确补偿方法。采用上述补偿方法对稳态电容电流的效果较好,而对暂态电容电流的补偿效果不好。对于特高压线路,采用稳态电容电流进行补偿的差动保护,在计算时需要较长的数据窗,往往无法满足其速动性的要求。对于长距离的特高压直流线路保护如何提高差动保护的可靠性,文献[7]在研究了故障暂态和稳态过程后,提出了根据故障分量电流极性的新型差动保护算法。文献[8]基于直流滤波器获取到的电流的频率特性实现了线路区内和区外故障识别。文献[9]分析了直流线路内部故障下两端电流的突变方向纵联保护判据,但没有把线路分布电容的影响考虑进来。对于线路全长3300多公里的准东—华东±1100 kV特高压直流输电线路工程,超长输电线路若不考虑分布电容电流对传统以基尔霍夫电流定律为基础的电流差动保护的灵敏性及可靠性的影响,差动保护可能会误动。
下面基于贝杰龙线路分布参数模型,讨论了选择不同参考点补偿电流的情况,确立了由首端实测电流和对端计算线路全长的电流以及由两端计算到线路中点的电流,构造了两个补偿电流比值的多点联合判据,实现了超长输电线路区内和区外故障的识别。采用比值的判据构造形式,使得区外故障下,其比值理论上为1,保护定值易于整定。同时增强了耐过渡电阻的能力。
1 长距离输电线路现行直流线路纵联差动保护动作的仿真分析
为研究长距离特高压直流输电线路的差动保护问题,搭建了适用于所阐述内容的仿真模型。所搭建的特高压直流输电系统模型是依据准东—华东±1100 kV特高压直流输电线路工程技术方案。正在建设的起于新疆准东五彩湾换流站,止于安徽皖南换流站的准东—华东±1100 kV特高压直流输电线路工程[10-11],其输送容量为12 000 MW,线路航空直线长度为2 997.1 km,全长约3 324.143 km(含长江大跨越3.143 km)[10-11]。其仿真模型如图1所示。额定电压为±1100 kV,额定电流为5.45 kA,送端换流站接入750 kV交流电网,受端换流站分层接入500 kV/1000 kV的交流电网,直流输电线路全长为3300 km,采用8×JL1/G3A-1250/70架空线路,采用LBGJ-240-20AC的架空地线[13]。每极采用两个12 脉动换流器串联的接线方案,线路两侧装有300 mH的平波电抗器,每站每极设置一组三调谐直流滤波器支路TT6/12/39,可以滤除掉6次、12次和39次谐波。接地极线路全长为81 km,采用2×2×JNRLH60G1A-630/45钢芯耐热铝合金绞线,地线采用JLB20A-100。
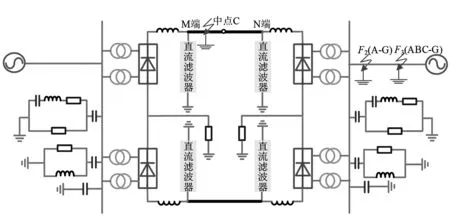
图1 ±1100 kV直流输电系统结构
行波保护只采用单端量,不需要对侧的信息,所以不用考虑信息传输延时对行波保护的影响[14],采用线路两侧直流电流的差值作为动作判据的纵联差动保护,其原理是以基尔霍夫电流定律为基础的,动作方程为
|irec-iinv|<Δiset
(1)
式中:irec为整流侧电流,pu;iinv为逆变侧电流,pu;Δiset为线路两端电流差动作整定值,这里取0.05 pu。由式(1)可知,理论上在线路未发生故障时,其线路两端获取的电流差值一般很小;而在线路发生故障时,其两端获取到的电流差值一般较大。在直流输电线路发生故障后,直流控制系统将快速抑制线路的故障电流。由于直流控制系统响应的叠加作用,很难做到单纯依靠差流的大小就能够有效判别是区外故障还是线路故障。实际直流工程中的直流线路差动保护多采用闭锁逻辑保证其选择性,然而以电流扰动为判据的闭锁逻辑加长了差动保护响应时间,导致直流控制系统的保护先动作,进而引起不必要的直流闭锁事故。
现假设正极直流线路距离整流侧M端500 km(F1)处发生金属性接地故障,两侧的差流如图2所示。逆变侧交流系统分别发生A相经10 Ω过渡电阻的接地故障(F2)和ABC三相金属性接地故障(F3),线路两侧瞬态电流差值如图3和图4所示。
从图2中可以看出,线路在发生接地故障时,由于有接地点的加入,其两侧差流到达整定值。同时通过控制系统的调节作用,电流值稳定于0.05 pu,大于纵差保护的整定值,差动保护正确动作。由图3、图4可知,当逆变侧交流系统发生故障,由于长线路分布电容的影响,两侧电流值存在延时,故其差值在一段时间内的变化幅度会很大,甚至超过了门槛值导致差动保护误动作。

图2 正极线路500 km金属性接地故障下的线路两侧差流变化曲线
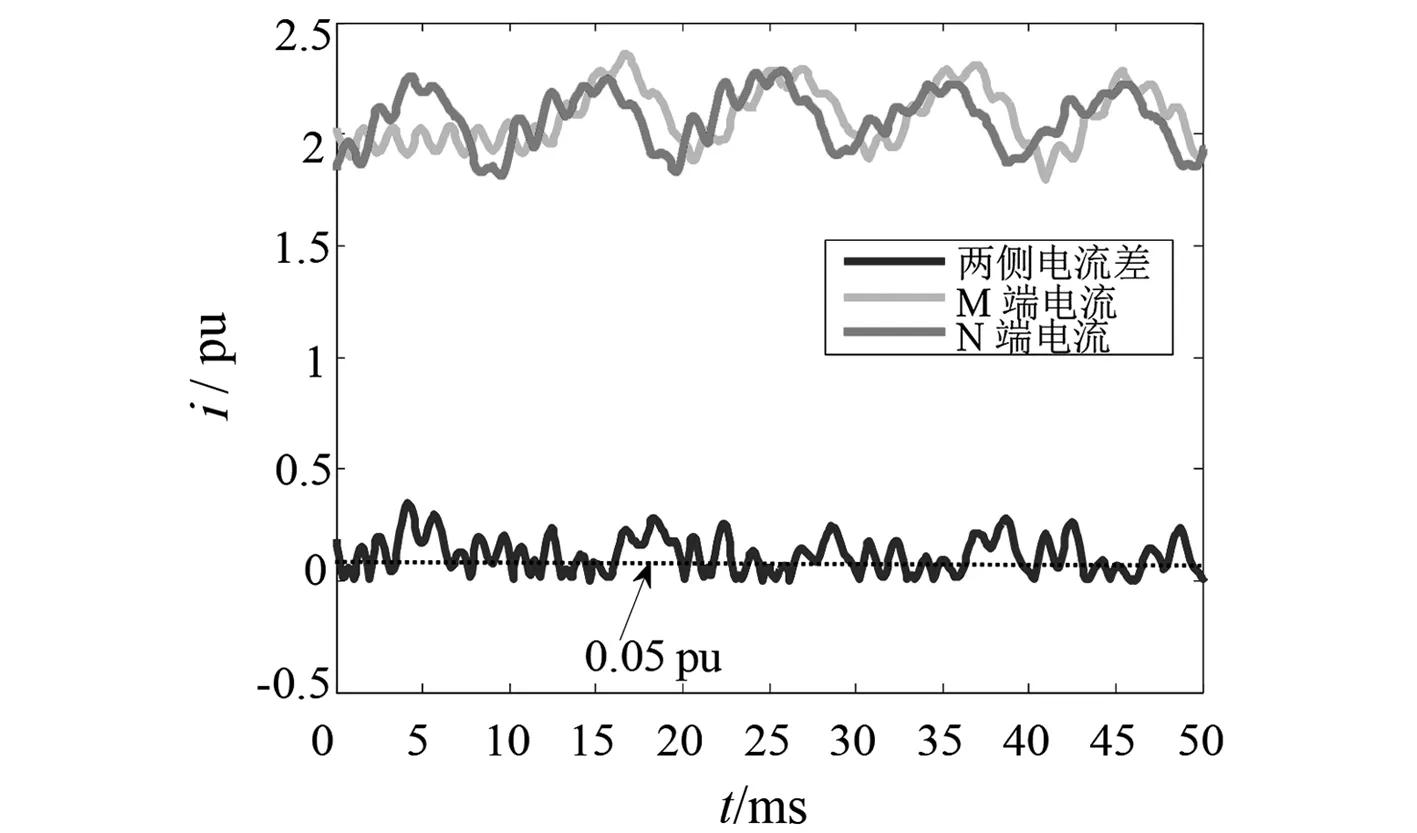
图3 逆变侧交流系统在A相10 Ω过渡电阻故障下的线路两侧差流变化曲线
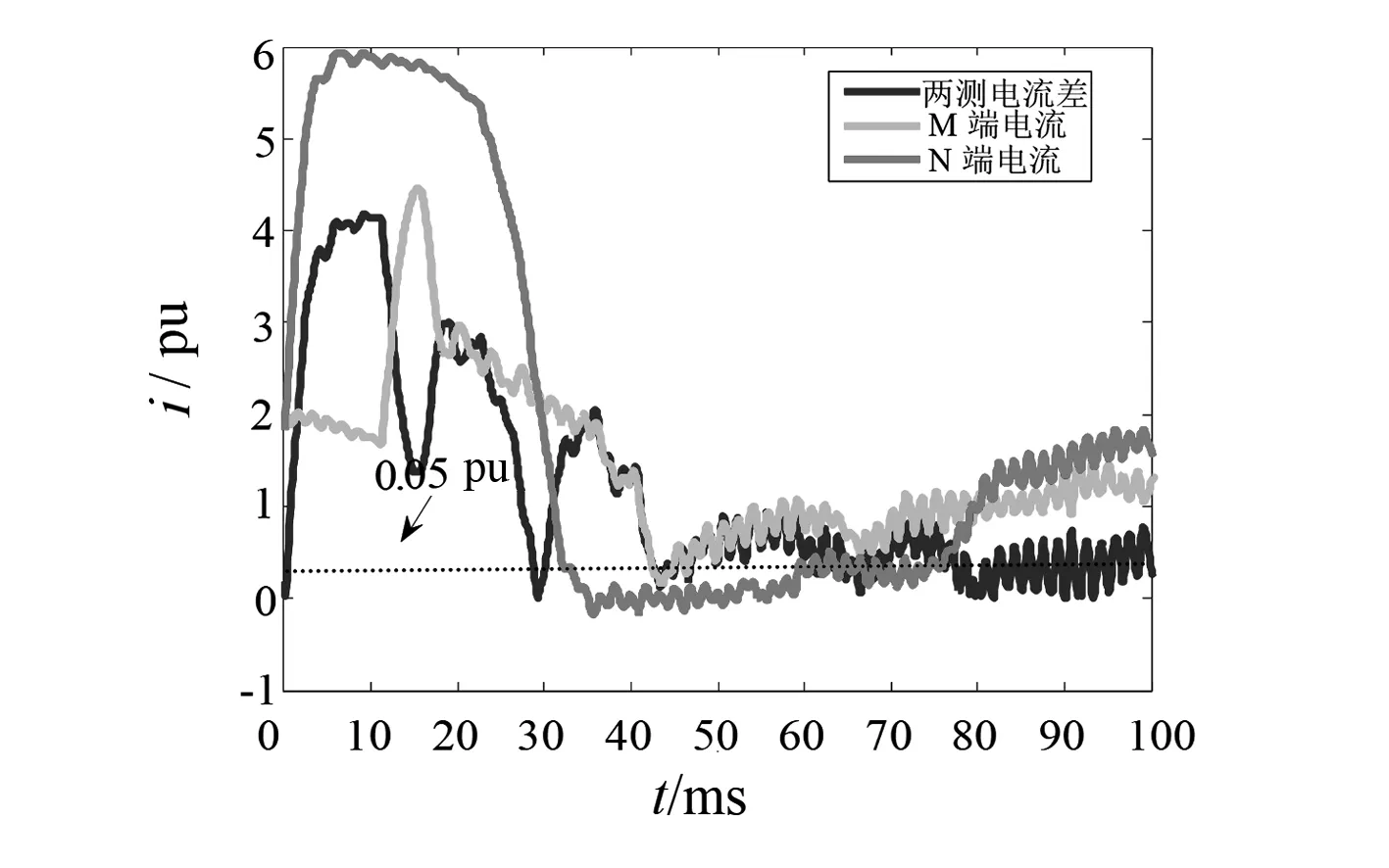
图4 逆变侧交流系统ABC三相故障下的线路两侧差流变化曲线
2 基于贝杰龙模型的沿线电流计算
为改进现有差动保护,提出了一种适用于长距离特高压直流输电线路的贝杰龙差动保护算法。特高压直流输电线路通常采用具有分布参数的均匀有损传输线的模型来描述,但要得到全频率下传输线的波动方程在计算上存在困难,对于保护来说可能影响速动性。贝杰龙模型可以发挥沿线高通滤波器的作用,将一段均匀有损传输线分成了2段均匀无损传输线路,其中每段的线路电阻分别集中到了线路两侧,能够以较高精度近似实际线路,如图5所示。在图5中:M、N为线路两端;k1、m1、k2、m2为线路节点,在等值电路计算中这些节点是独立的;l为线路全长;r为线路等效电阻。

图5 贝杰龙线路模型
对于无损传输线,该时域模型如图6所示。在图6中:uM(t)、uN(t)分别为M端、N端t时刻的电压;iM(t)、iN(t)为分别为M端、N端t时刻的电流;Zc为线路波阻抗;iM(t-τ)、iN(t-τ)分别为M端、N端t-τ时刻的电流。

图6 无损传输线路的时域等效电路
由图6可知,沿线电流、电压分布的表达式可用M端的电气量表达,如式(2)所示。
(2)
式中:uM、iM分别为M端电压、电流;Zc为线路波阻抗;v为线路传播速度;x为距离整流侧M端的距离。
贝杰龙时域模型是无损传输线时域等效电路的一种改进,其等效电路如图7所示。
根据图7,由M端和N端计算的沿线电流分别为:
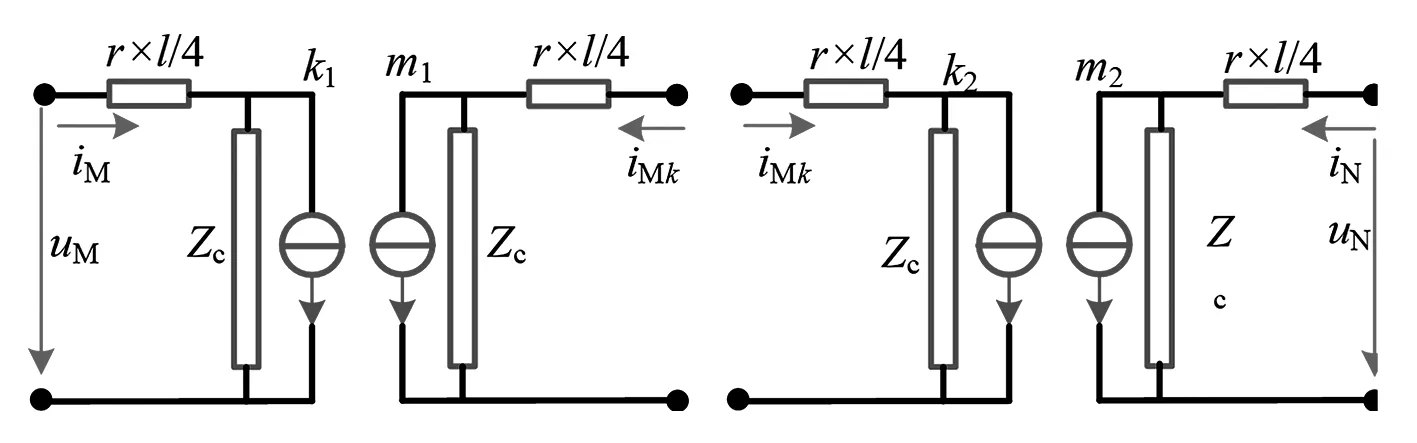
图7 贝杰龙传输线路时域等效电路
(3)
(4)
式(3)、式(4)中:下标s表示模分量,s=1表示线模分量,s=0表示零模分量,接下来的计算中选取s=1线模分量计算电流;r为线路等效电阻;uN,s、iN,s分别为N端电压和电流。
3 多判据联合的纵联差动保护
基于贝杰龙模型差动保护的核心原理是:根据量测端M、N的电压、电流用式(3)和式(4)计算出参考点两侧的电流,如果故障存在于线路内部,两侧电流计算值也不满足基尔霍夫电流定律,就能够区分出区内故障和区外故障。
若选取线路全长首端(M端)为参考点,则可知线路发生区外故障理论上满足式(5)。
iM0,ex(t)-iNl,ex(t)=0
(5)
式中,下标ex表示区外故障。因此,将M端作为参考点,且M端起始电流为iM0,ex,由N端计算得到的电流iNl,ex越接近M端电流,计算得到的电流差值越小。
若选取线路中点作为参考点,则可知当故障位于线路中点和区外故障时理论上满足式(6)。
(6)
式中,下标l/2表示线路中点。由式(6)可知,当线路发生中点故障和区外故障时,电流差值最小。
可以将式(5)和式(6)改写为
(7)
由式(7)可知:当发生区外故障时,由M端推算到N端的电流与M端量测得到的电流比值为1,同时也满足分别由N端和M端推算至中点的电流的比值为1;当线路发生中点故障,分别由M端和N端推算至中点的电流的比值为1。而故障位于其他位置时,将不满足式(7)。由于采用式(7)不容易构造保护判据,现定义补偿电流比值为kj,其表达式为
(8)
式中:j表示取不同参考点,若j=M,即kM为参考点M时的补偿电流比值,若j=C,即kC为参考点l/2时的补偿电流比值;Δt为积分时长,Δt=l/vs。
4 基于贝杰龙模型的差动保护流程及仿真验证
基于上一章的描述,本章将基于贝杰龙模型的差动保护流程描述如下:
1)获取故障时M端和N端电压、电流行波数据。
2)利用贝杰龙线路模型,分别由M端和N端计算线路中点电流iMl/2,s(t)和iNl/2,s(t),并根据式(8)计算得到补偿电流比值kC,若比值kC>1.1或kC<0.9,则判断为线路故障;若不满足,则转入下一步。
3)利用贝杰龙线路模型,由N端获取的电压电流数据计算M端的电流,并与M端获取的实测电流计算出补偿电流比值kM。若kM>1.1,则判断为线路故障;若kM<1.1,则判断为区外故障。
通过图1的仿真模型验证上述基于贝杰龙模型的差动保护方法,其仿真结果如表1所示。在表1中:xf表示距离整流侧M端的距离;Rf为接地点过渡电阻;Result 1为采用kC的判断结果;Result 2为采用kM的判断结果;Result为综合判断结果;Ⅰ为整流侧交流系统ABG接地故障;Ⅱ为整流侧交流系统ABCG接地故障;Ⅲ为逆变侧交流系统ABCG接地故障。
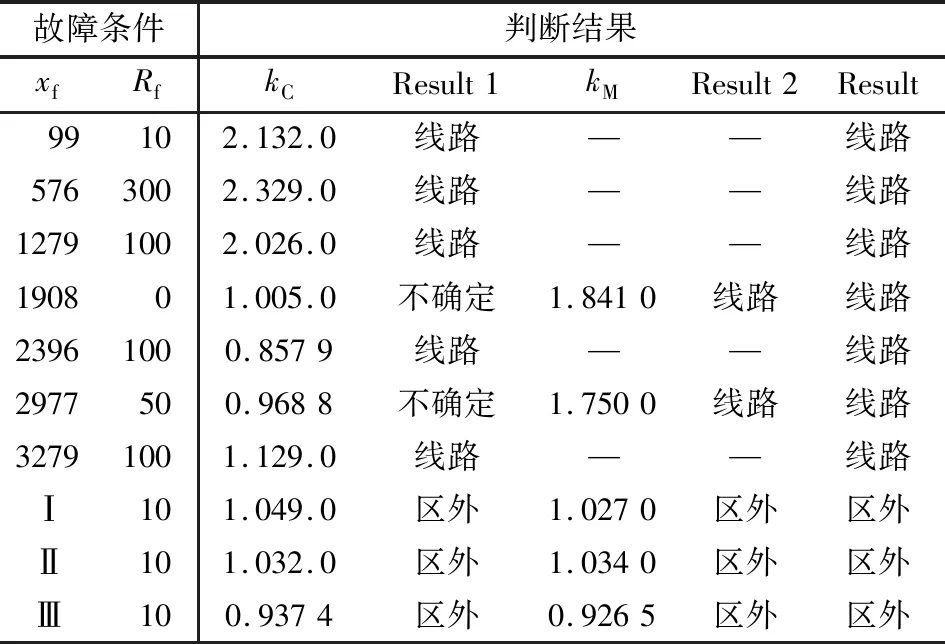
表1 基于贝杰龙模型多点联合方判断方法的仿真数据测试结果
同时于线路全长范围内遍历不同位置的故障,得到参考点为M端和l/2下的kM和kC如图8(a)所示;对于区外故障考虑不同的故障条件,得到kM和kC分别如图8(b)所示。图8中:1#为整流侧出口故障;2#、3#以及4#分别表示整流侧AG、ABG 以及ABCG金属性接地故障;5#为逆变侧出口故障;6#、7#以及8#分别表示逆变侧AG、ABG 以及ABCG金属性接地故障。
理论上,区外故障下求取得到kM和kC的值均为1,考虑到各种工况引入的误差,将门槛值取为kset1=1.1和kset2=0.9。由图8(a)可知,若取kset1=1.1和kset2=0.9,则采用补偿电流比值kC在1900~2400 km容易出现误判,而采用kM时,由仿真得到的数据在全线范围内均大于kset1,但考虑到理论上分析越接近N端,其值应该越接近1,同时考虑到噪声、采样率以及计算引入的误差,可能会使计算的值接近1,而无法可靠判断。因此引入“弱置信度判断区”来表征保护与该区域的可靠性较低,需要增加其他的可靠性。例如表1所示的结果,当线路于2977 km发生接地故障,计算出来的kC=0.966 8,这个结果不可靠,因此通过计算kM=1.750,可确定是线路故障。这里所谓的“弱置信度判断区”概念,是结合理论和仿真分析对保护判据在某个线路段的判断结果可靠性进行评估。保护判据对于不同部分(如不同的线路段)其可靠性不同,对其进行置信度的评估可以提高保护判据的可靠性,也是后续要研究的内容。

图8 仿真得到的全线长范围内和各种区外故障下的kM和kC
5 结 论
对于具有明显分布参数特性的长距离直流输电线路,提出了基于贝杰龙模型的电流差动保护方法,并根据M端和N端观测数据推算出沿线多处位置的电流差形成多点联合判定的纵联保护,具有以下特点:
1)考虑了线路的分布参数特性,采用多点联合的判据,可以进一步减小分布电容电流对保护判据的影响;
2)采用比值的形式构造保护判据,使得区外故障下,其比值理论上为1,易于构造保护整定值,且受故障电阻的影响小。
