浮动式制动闸片压力分布的数值模拟*

2021-11-19陈吉光

铁道机车车辆 2021年5期

陈吉光

（大连交通大学教育部连续挤压工程研究中心，辽宁大连 116028）

列车盘式制动器具有较好的制动效能和稳定性，是高速列车的必备安全装置。列车紧急制动时制动盘和闸片由于剧烈摩擦产生大量热量，使制动盘和闸片的温度急剧升高。张建等在研究中注意到制动盘转动状态下，接触压力中心向转动方向移动，与摩擦块形心之间发生偏离，压力分布非常不均匀［1］。

德国铁路公司较早提出了改善接触模式的ISOBAR™新型闸片使得制动盘上所有点的压力均衡化，提高重载制动盘性能，并减少制动器噪声。其在结构上消除了传统UIC 闸片用燕尾槽安装与插板固定的缺点，使闸片和制动盘的磨损显著减小，峰值温度也从900 ℃左右降到600 ℃［2］。

弹性结构闸片在摩擦块与闸片钢背之间安装有弹性元件，可在一定程度上实现闸片的弹性调整，提高制动过程中的有效接触面积、降低噪音如图1 所示；王磊等设计的某浮动式制动闸片有3 级调整机构，与制动盘接触均匀，可避免摩擦块损伤，减少制动盘热斑和裂纹，用于300 km/h 以上高速列车上［3］。

图1 浮动闸片原理

文中讨论针对浮动式制动闸片进行数值模拟，采用有限元热机耦合法去分析和揭示其压力分布改善的作用机理。

1 研究现状

1.1 热机耦合分析方法（温度场、热弹性变形、应力场）

摩擦热导致摩擦材料发生热降解、变形、粘结剂气化，摩擦因数发生变化，制动性能降低，出现热衰退现象；也使制动盘发生局部材料的相变与热变形，出现局部热点［4］。由于制动盘和闸片的接触变形和磨损导致接触界面变化剧烈，制动力在接触界面上的分布是极不均匀，并导致温度场的不均匀分布，制动盘和闸片产生热弹性变形，进而引起摩擦副接触状态和接触压力的变化，宏观上容易观察到制动盘出现热斑或热条带［5］。摩擦副服役期间反复升温与冷却的循环还会导致制动盘热疲劳裂纹，热疲劳开裂和磨损是高速列车制动盘失效的主要形式［6］。微观上由于摩擦材料第三体的形成和剥落对瞬时实际接触面积、应力集中以及磨损量的影响造成了接触状态和接触压力剧烈变化［7］。

温度和压力传感器都无法安置在摩擦界面，使得接触界面的表面测试技术成为一个十分棘手的问题，接触表面的最高温度在接触处瞬时形成的闪现温升，接触位置时刻发生变化，因此，试验手段只能是间接测量，难以准确反映出变化过程和变化状态。盘形制动过程中的摩擦生热问题是典型的热—结构耦合问题。有限元软件能分析摩擦副在滑动摩擦过程中，受摩擦热和力场的耦合作用下，接触区域表现出的局部温度变化、应力变化等特性，揭示接触过程中材料表面磨损。

耦合场分析是指在有限元分析的过程中考虑了多种物理场的交叉作用和相互影响（耦合），热—机耦合被用来分析材料特性、背板厚度、摩擦系数、制动钳的变形等对接触压力的影响，还能分析接触压力分布与磨损、热点、表面裂纹和应力等之间的影响关系。例如，Talati 发现摩擦热的产生与接触压力的大小直接相关，而温度分布的不均匀性导致物体的热变形差异又直接影响接触状态或接触压力，接触状态的改变反过来影响摩擦热流分布［8］。OUYANG H J 等认为由于热变形接触区和压力分布同时改变，热和机械变形彼此强烈和同时影响，摩擦界面存在不均匀温度影响下的接触压力［9］。黄健萌在盘式制动器热—结构耦合的数值建模与分析中证实物体的热变形差异直接影响接触状态或接触压力［10］。王仕仙用ANSYS 分析了摩擦滑移过程中，瞬时高温的热点会造成摩擦表面的黏着磨损［11］。张立军认为摩擦力引起的载荷转移效应促使盘块接触压力总体上向进摩擦区方向偏移，闸片的径向接触压力梯度导致摩擦块复杂的温度分布特征［12］。赵海燕则采用MSC Marc 软件分析了160 km/h 快速列车制动盘温度场制动热过程分析，由于接触区的温度不均匀性，采用均布制动载荷方式不利于闸片的均匀磨损［13］，夏毅敏用ANSYS 软件建立了高速动车组制动闸片热力耦合三维仿真模型。仿真得到闸片温度达到最大值535 ℃，闸片应力达到最大值333 MPa［14］。

1.2 浮动结构制动闸片

目前高速列车上普遍采用了新型浮动式结构闸片如图2 所示，实现闸片与制动盘的最大贴合，极大地提高制动效率，有效避免因闸片受力不均而产生制动盘热斑。

图2 浮动闸片三维模型

在不改变盘式制动器的整体结构情形下，改进制动盘或制动闸片是2 种可行的途径。Roches对比了3 种TGV 火车制动刹车片设计，第1 个9 个圆形摩擦销通过金属环固定在背板上，第2 个增加了背板和10 个多边形摩擦销之间连接的灵活性。第3 个是9 个圆柱形引脚固定在坚固的背板上的旧设计，试验验证了改进闸片结构能提高制动器性能［15］。王磊设计的浮动式制动闸片，摩擦块在制动力作用下可通过调整器上面的球窝自动调整摩擦平面，调整器可在高度微调，通过两级球面和球窝相互配合，实现制动闸片与制动盘的最大贴合，极大地提高了制动效率，有效避免了由于制动闸片受力不均而使制动盘产生热斑的现象［16］。李继山等研制的粉末冶金闸片采用弹性结构。摩擦块固定在钢背上，钢背的另一侧与支撑件相对设置，钢背通过弹性元件可浮动地支撑在支撑件上，解决了闸片垂向受力不均匀问题［17］。曲选辉通过调整闸片的形状与排布，调整闸片接触表面的压力大小和分布，闸片摩擦块安装在弹性元件上，并通过卡簧连接在背板上，使用中自适应性浮动，减轻了偏磨现象［5］。

弹性结构使闸片摩擦面受力更加均匀，且能有效降低振动带来的磨损伤害。Kapob 指出用闸片接触斑的平均数目来衡量其性能，为了使物体上的法向力均衡地压向物体，并保证围绕接头无转动力矩需要有3 个接触点［18］。

1.3 磨损因素的影响

由于计算量很大，三维有限元模型中很少考虑制动器的盘和闸片界面处的磨损。磨损会对制动器中摩擦界面的温度和压力分布的产生影响，使得局部高界面压力的区域也将是高表面温度的区域［19］。制动器磨损会导致一系列问题的出现，直接影响制动器的使用寿命和行车安全性。热磨损是由交替变化的温度所导致摩擦材料和摩擦界面发生的一系列物理和化学变化，杨磊分析了盘式制动器热磨损产生的机理以及降低热磨损的新方法［20］。李玉龙通过铜基摩擦片不同制动速度以及制动压力下摩擦系数和磨损率的变化规律，得出磨损率随制动压力增加而增加［21］。Gyimah 开发了一种高压盘式制动测试仪来测试材料的磨损行为。试验表明高温烧结的摩擦系数，磨损率和磨损量均有较大幅度的提高［22］。

2 数值模型和计算方法

2.1 接触问题

耦合场的分析有序贯耦合法和直接耦合法。序贯耦合解法是按照顺序进行多次的相关场分析，把第一次场分析的结果作为第二次场分析的载荷来实现2 种场的耦合，方便有效。直接耦合解法适合高度非线性问题，仅一次求解就能得出耦合场分析结果。接触问题就是一种高度非线性问题，需要极大的计算资源，合理建模非常重要。接触问题存在2 个较大的难点，一是用户求解问题之前，用户不知道接触区域；二是大多的接触问题需要计算摩擦，摩擦定律和模型都是非线性的，摩擦使问题的收敛性变得困难［23］。非线性有限元模拟制动性能，但用精确的数值模型模拟完整的工业模型需要高昂的计算成本。因为接触处理需要较小的时间步长，大约10-6s，这使得1 s 的数值模拟所用计算时间都很长。Roches 曾估算在600 000个自由度系统上使用非线性隐式算法在700 多个h内会产生超过1 TB 的数据［15］。

2.2 有限元算法选取

隐式求解一般用于线性分析和非线性结构静动力分析，静态松弛法将动力学问题看作静力学问题来解决，每一步需要数值阻尼达到静力平衡。对于线性结构的瞬态动力学平衡方程为式（1）：

隐式算法纽曼法（Newmark）进行时间域的积分，纽曼法中任一时刻的位移、速度、加速度都相互关联，这就使得运动方程的求解变成一系列相互关联的非线性方程的求解，这个求解过程必须通过迭代和求解联立方程组才能实现。隐式求解法可能遇到两个问题：一是迭代过程不一定收敛，二是联立方程组可能出现病态而无确定的解。但优点是它具有无条件稳定性，即时间步长较大。隐式求解法不考虑惯性效应［C］和［M］。对于非线性问题，通过一系列线性逼近（Newton-Raphson）来求解；要求转置非线性刚度矩阵［K］，收敛时候需要较小的时间步，对于高度非线性问题可能无法保证收敛。

纽曼法使用有限差分法求解瞬态问题，主要目的就是计算下一时刻的位移un+1，则在tn+1时刻的控制方程为式（2）：

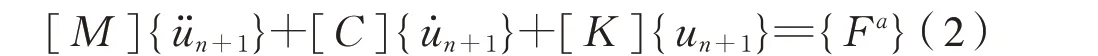
2.3 数值模型

闸片和制动盘的简化模型如图3、图4 所示，制动盘不考虑内部通风筋，简化为摩擦环，材料为钢（密度7.8 g/cm3；热容量430 J/（kg⋅℃）；温度20 ℃）。摩擦块为六角形，共18 个，闸片摩擦面积400 cm2（粉末冶金摩擦块密度5.4 g/cm3；热容量600 J/（kg⋅℃）；温度20 ℃）。

图3 燕尾式模型中，18 个六角形摩擦块与背板的接触设定为具有较大的刚度，模拟摩擦块与背板的紧固连接，制动力施加在燕尾处；在图4 的浮动式结构模型中，18 个六角形摩擦块与背板的弹性浮动结构，在有限元模型中简化为接触具有较小的刚度，使得摩擦块相对与背板能有一定程度的“自由摆动”。接触刚度K的作用在下节（3）式中用到。

图3 燕尾结构闸片和制动盘

图4 浮动结构闸片和制动盘

3 数值模拟结果分析

摩擦接触必须使用非对称刚度矩阵，通过命令NLGEOM，ON 设定允许大变形和非线性；命令NROPT，UNSYM 选取完全牛顿-拉夫逊法算法，适合求解高度非线性问题。

3.1 在22.5 kN 压力下摩擦界面的压力分布

模型中各个有限元单元在接触区的三方向受力的向量可表示为式（3）：

式中：P为正压力（法向，z 向），P=Ku，N；Tx，Ty为剪切接触应力，N。满足式（4）：

式中：μ为摩擦系数，取0.4；K为接触刚度系数，N/m；u为位移，m。

在制动开始时，制动盘高速转动，给定转动速度为183 rad/s（300 km/h）。制动夹钳压力逐渐从0 增大到22 500 N，闸片与制动盘逐步紧密贴合，在接触界面的摩擦形成了制动力，由于摩擦力的剪切作用，接触界面的压力分布并不均匀，如图5 所示，数值见表1。最大变形量燕尾结构为2.738 4×10-5m，浮动结构为1.788 8×10-5m。

图5 闸片接触压力分布(仅制动力)

3.2 耦合温度场热变形对摩擦界面的压力分布的影响

制动过程中，随着时间的推移，剧烈的摩擦和大量的摩擦热使得制动盘、闸片、背板都产生了热变形，影响了摩擦副表面的形态，造成接触界面压力分布的改变。

物体因温度梯度引起的热变形为式（5）：

式中：L为长度，m；α为线膨胀系数，m/K；T为温度，K。

采用热机直接耦合计算温度场和热变形的计算量太大，使得计算几乎无法完成，大多学者专注于制动盘和闸片的温度场研究，证实采用外源热传导计算仍能得到较为可信的结果，而该方法计算效率高［10，13，20］。通常将摩擦热以外源热流的方式施加到摩擦界面上，计算热传导和热传递为式（6）：

式中：q为热流密度，W/m2；v为速度，m/s；A为摩擦面积，m2。

计算闸片最高温度580 ℃，再将温度场耦合到结构分析中，施加制动力22 500 N 得到考虑热变形后的压力分布如图6 所示，数值见表1。最大变形量为燕尾结构为2.202 6×10-3m，浮动结构为1.485 8×10-3m。可见热变形的影响比较显著。

图6 闸片接触压力分布（耦合热变形）

3.3 耦合磨损对摩擦界面的压力分布的影响

Archard 黏着磨损是运用较为广泛的磨损模型，但准确参数难以确定，BAKAR 在磨损界面的磨损随着时间的推移使用修改的磨损率公式进行模拟，磨损公式的通过试验结果测量验证［24］。

在摩擦界面，由于制动盘的硬度远高于闸片的硬度，所以只考虑闸片的磨损，其磨损量约为0.12 cm3/MJ［16］。根据Archard 磨损公式，磨损体积为式（7）：

式中：V为磨损体积，m3；K为磨损率，无量纲；H为材料硬度，N/m2；s为磨损路程，m。

磨损模型接触副为有摩擦非对称接触，式（7）的磨损参数用TB WEAR 和TB DATA 输入。非线性接触算法是增广拉格朗日罚因子方法，接触采用节点判断，时间步长较小，为10-6s。如需记录接触压力、接触状态、间隙、磨损、滑动位移等，设置关键字NLDIAG、CONT、ON。计算结果如图7所示，其接触压力对比见表1。