基于试验设计的制动系统产品模型优化

韩朝霞，李邦国,2，王群伟,2

（1 北京纵横机电科技有限公司，北京 100094；2 中国铁道科学研究院集团有限公司 机车车辆研究所，北京 100081）

制动系统直接影响高速列车的行车安全，制动系统的各关键组成部件的稳定性和可靠性是当前研究的重中之重。制动系统产品在设计过程中采用试验设计［1］的方法能缩短设计周期，减少设计成本，且能进行故障诊断。从质量发展的过程来看，从原来的“质量是检验出来的”提升到“质量是制造出来的”并最终发展到“质量是设计出来的”。试验设计在产品的研发阶段占有重要地位，也决定着产品的生命周期与质量水平。铁路制动系统产品运用试验设计的理论及方法，能够大大提高试验的效率，创新的效率以及制动系统产品的竞争力。

1 试验设计理论

试验设计是研究正确的设计试验计划和分析试验数据的理论和方法，通过改变设计过程中的输入（控制变量），观察输出（响应变量）的变化，从而获取关于整个设计过程的全套知识，确定各个输入因子的重要性等级及其对输出的影响程度，并达到最优化过程的目的。试验设计的研究过程如图1 所示。

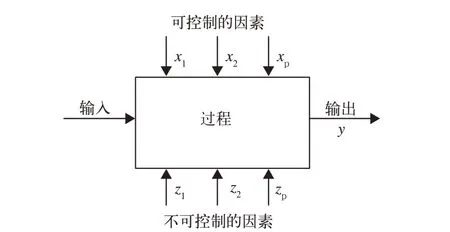
图1 试验设计研究过程

由图1 可知，试验设计过程是把一些输入转变为有一个或多个可观察响应的一种输出，过程中包含可控因子以及不可控因子。输出是由输入、可控变量以及不可控变量共同作用的结果，y=f（x）就是探索y与x的关系，需要确定4 个方面的内容：

（1）确定哪些变量对响应y最有影响。

（2）确定有影响的x设置在何处使得y几乎总是接近于所希望的额定值。

（3）确定有影响的x设置在何处使得y的变异性最小。

（4）确定有影响的x设置在何处使得不可控变量的效应最小。

试验设计在设计开发和为改善性能的故障分析中起重要作用，多数情况是设计开发一种受外部变异性来源影响最小的设计方案。

2 减压阀的试验设计

铁路车辆上某些已投入使用的减压阀，在经过一段时间运用之后，会产生强烈噪声，甚至影响到乘客乘坐列车的舒适性。为了解决减压阀的噪声问题，需要对减压阀进行分析，找出引起噪声的关键因子，并进行模型优化。对减压阀进行试验设计的操作步骤如图2 所示。

图2 试验设计步骤

2.1 目标分析

针对噪声减压阀，判断减压阀噪声原因可分为以下3 类：

（1）减压阀机械振动噪声。

（2）流体动力学噪声。

（3）空气动力学噪声。

通过对噪声的时域信号如图3 所示，进行频率分析如图4 所示。

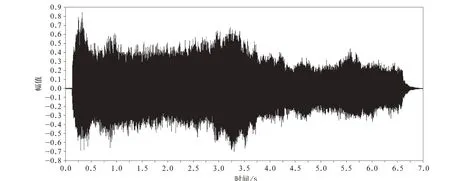
图3 振动噪声时域信号

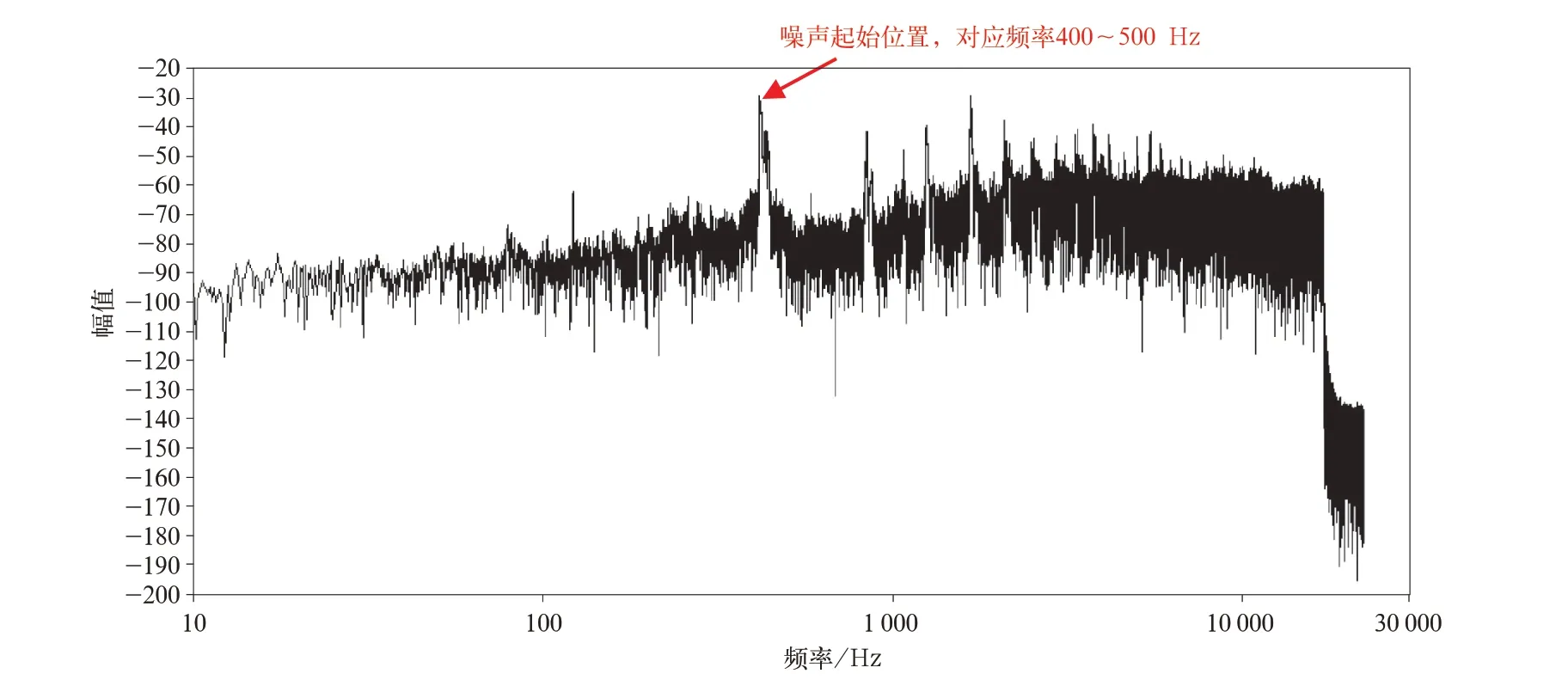
图4 振动噪声频谱分析

由图4 可知，在噪声起始位置，其频率在400～500 Hz 之间。推断减压阀的噪声是由于空气压力波动的激振频率和减压阀本身的弹簧质量系统振动频率接近而产生。因此改变空气压力波动的激振频率或者改变弹簧质量系统的固有频率，均有可能消除减压阀的噪声。下面将建立减压阀的详细模型进行仿真计算，探究空气流动造成振动的因子，并通过改善这些因子来达到消除振动的目的。

2.2 建立减压阀模型

根据噪声减压阀参数，建立减压阀模型，如图5 所示。

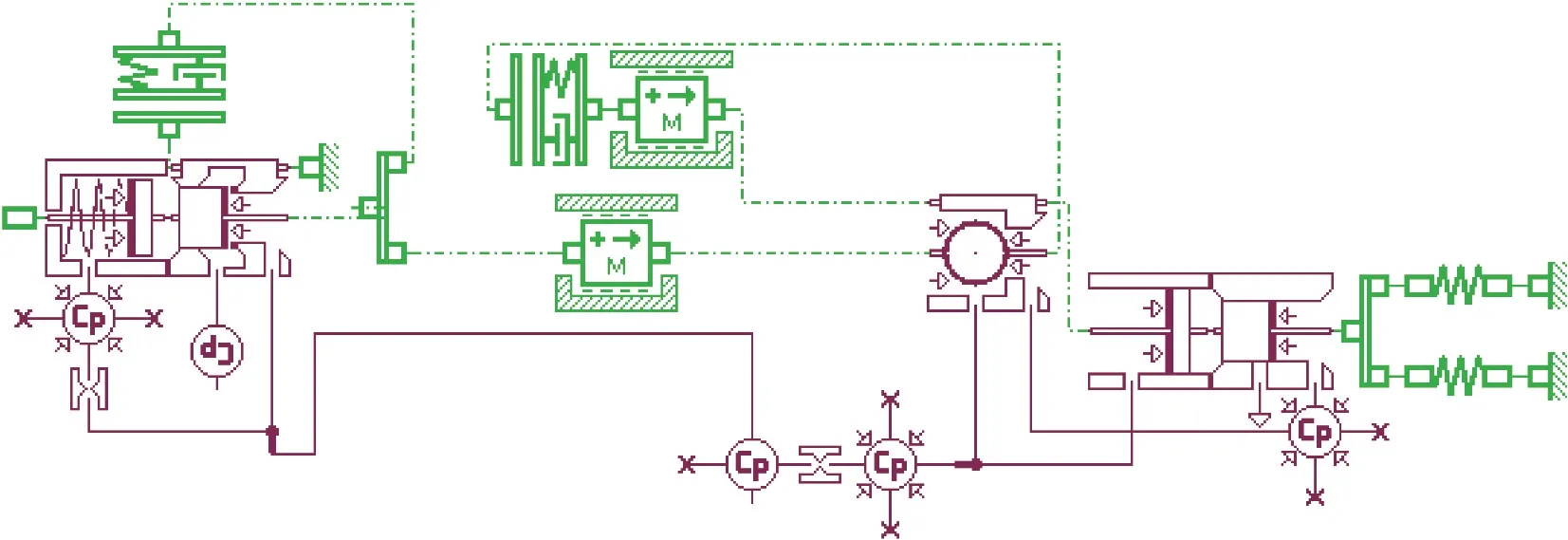
图5 减压阀模型

运行仿真，减压阀的出气口压力波形和溢流口开度（位置见图5）如图6 所示，由图6 可知当压力发生波动的时候，大活塞发生振动。由于溢流口开度为正，溢流口排风，对时域的压力信号以及溢流口开度进行FFT 变换［2］，得到频谱图如图7 所示。从图中可以看出活塞的振动频率跟随压力波动的主激振频率，且此值为400～500 Hz 左右，与实测噪声起始位置的频率相近。由此可以验证减压阀的噪声是由压力波动导致的大活塞振动并发生溢流产生。

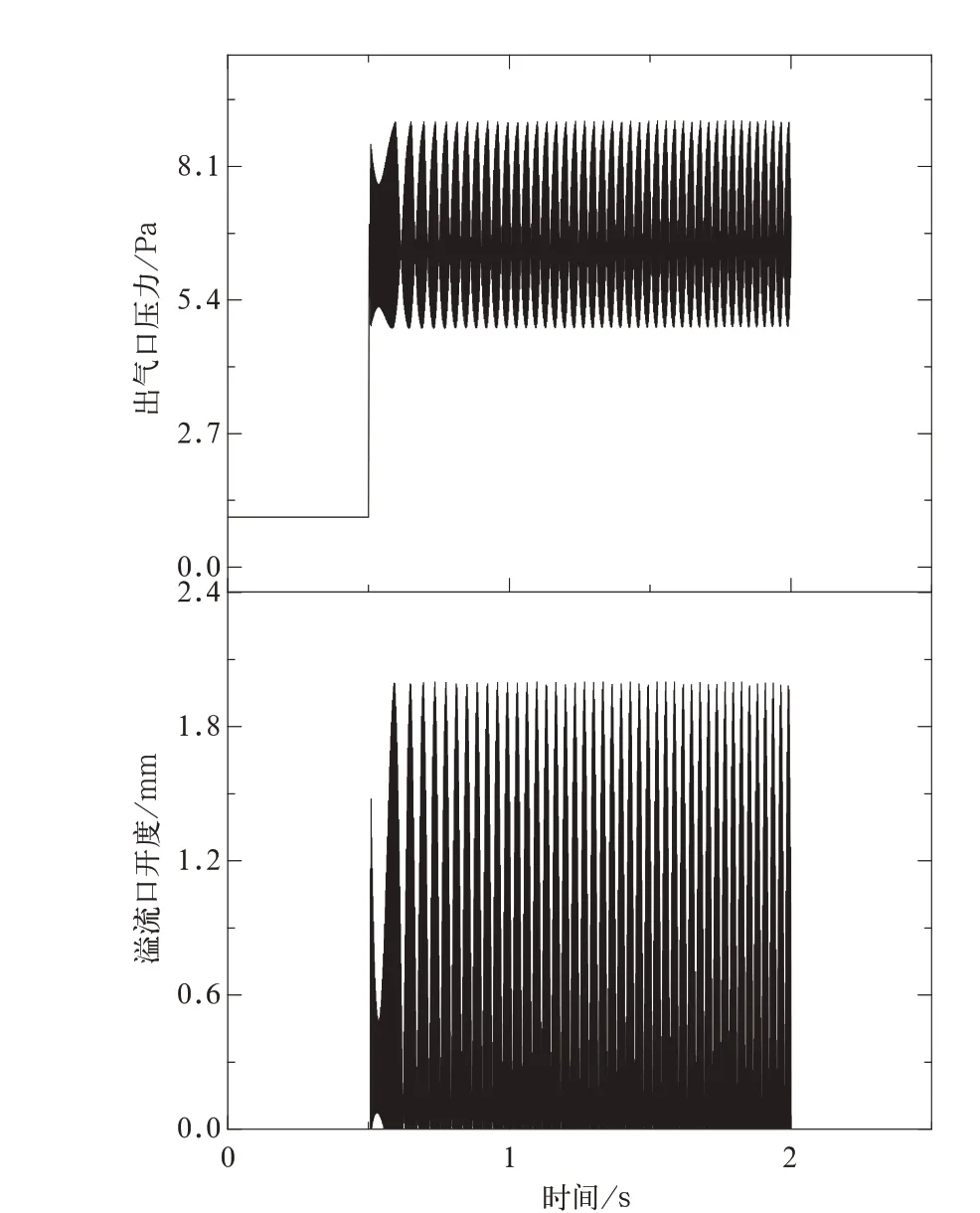
图6 出气口压力及溢流口开度

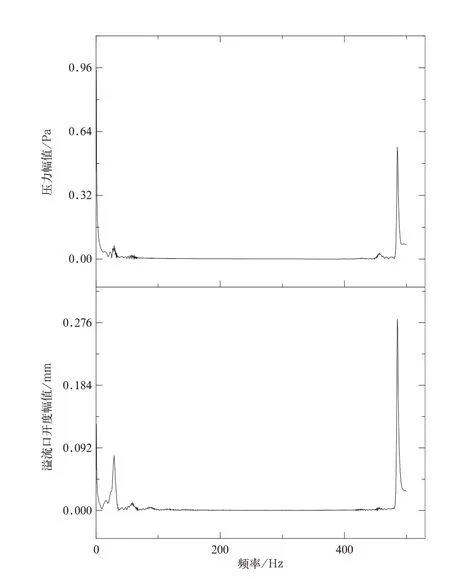
图7 压力及溢流口开度FFT

2.3 进行DOE 探索

2.3.1 明确优化指标

根据以上分析，明确试验设计的优化指标：

（1）出气口压力波动尽可能小。压力波动是所有振动发生的根源，控制压力波动的幅值和频率可以从根源上抑制噪声的发生。

（2）大活塞运动的速度尽可能平缓。大活塞的运动是导致减压阀机械振动的原因，控制大活塞的运动状态，可以控制机械振动的产生。

（3）尽可能使溢流口开度不大于零。大活塞的位移大于零时，减压阀发生溢流现象，产生噪声。因此控制溢流口开度，可以控制噪声的产生。

2.3.2 选择响应变量

根据以上优化指标，确定响应变量有3 个，分别为出气口最终压力（FinalOutP），大活塞最大速度MaxVelo，溢流口开度最大值（MaxOverflowDisp）。

2.3.3 选择控制变量

为筛选出对响应变量有影响的因子，首先进行单因子分析，选取对响应变量有较明显影响的因子有10 个，见表1［3］。

表1 影响因子列表

2.3.4 试验设计分析

在上文减压阀模型基础上创建全因子的试验设计，总计包含1 024 次试验，部分设计矩阵如图8所示。

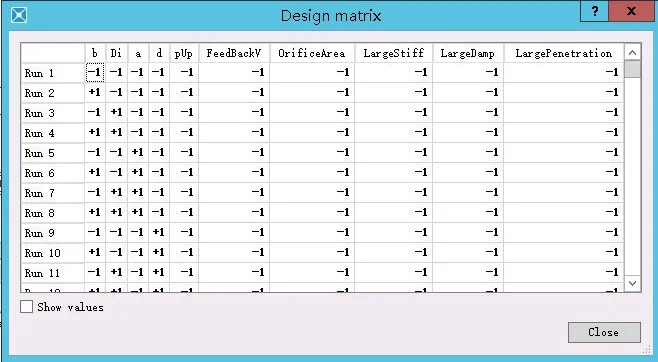
图8 试验设计设计矩阵

按照以上的输入因子以及输出响应设置，计算得到对应3 个响应变量MaxVelo、FinalOutP、MaxOverflowDisp 的10 个输入因子的线性回归系数，见表2。

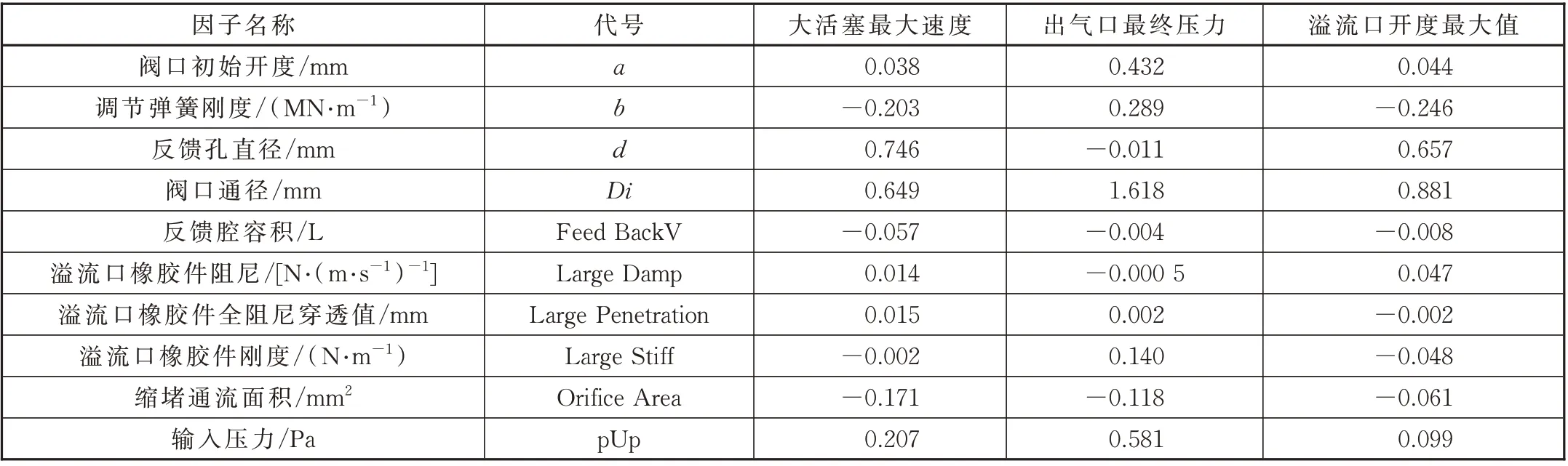
表2 输入因子线性回归系数

由表图可知，对MaxVelo 响应变量影响明显的输入因子分别为反馈孔直径d、阀口通径Di、输入压力pUp、调节弹簧刚度b以及缩堵通流面积Ori⁃ficeArea。对FinalOutP 响应变量影响明显的输入因子为阀口通径Di、输入压力pUp、阀口初始开度a、调节弹簧刚度b、溢流口橡胶件刚度LargeStiff 以及缩堵通流面积OrificeArea。对MaxOverflowDisp 响应变量影响明显的输入因子阀口通径Di、反馈孔直径d以及调节弹簧刚度b。其中输入压力pUp 在其范围内会受整个制动系统耗风量的影响，为不可控因子。

定义出气口最终压力值为约束：希望输出量的值不超过规定值的±0.1 Bar。配合MaxOver⁃flowDisp 响应变量的主要影响因子，选定目标量为大活塞最大速度MaxVelo，即大活塞最大速度Max⁃Velo 输出的绝对值越小越好。

在减压阀模型基础上建立4 因子，反馈孔直径d、阀口通径Di、调节弹簧刚度b以及缩堵通流面积OrificeArea 试验设计，设计矩阵如图9 所示，并绘制pareto 图，图中每个直方形代表给定因子所起作用的百分比，如图10 所示。

由图9 可知，对目标量大活塞最大速度Max⁃Velo 影响最显著的因子为反馈孔直径d，阀口通径Di以及2 因子的交互作用，总计占比70%，且其对目标量的作用均为正面作用，即反馈孔直径d越大，目标量大活塞最大速度MaxVelo 越大；阀口通径Di越大，目标量大活塞最大速度MaxVelo 越大；弹簧刚度越小，目标量大活塞最大速度MaxVelo 越大。其中反馈孔直径d，阀口通径Di为设计阶段可控变量。当选定弹簧材料时，运用过程中弹簧弹性衰减趋势为不可控变量。

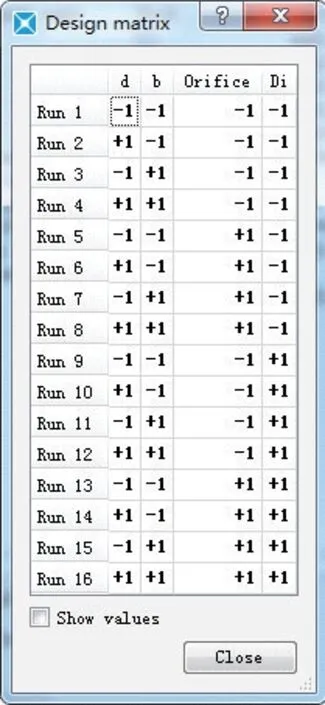
图9 4 因子试验设计设计矩阵

综上所述，确定反馈孔直径d，阀口通径Di两因子为影响减压阀稳定性和可靠性的关键因子，下文结合关键因子进行减压阀的参数优化。

2.4 减压阀参数优化

（1）优化算法

采用NLPQL（Non-Linear Programming by Qua⁃dratic Lagrangian）算 法［4］进 行 减 压 阀 的 目 标 优 化。NLPQL 算法是一种基于采用目标函数和约束的梯度来解决非线性优化问题的SQP 方法的实现。需要AMESim 来计算目标函数和约束在设计空间所有方向上的梯度，在优化过程中的每一输入参数均是一个方向。AMESim 使用有限差分方法来计算这些梯度。

设目标函数z=f(x，y)，其中，z为大活塞最大速度MaxVelo，x为反馈孔直径d，y为阀口通径Di，该函数的梯度为：

δ是相对梯度步长。首先程序根据x=x0，y=y0计 算f(x0，y0)，而 后2 次 运 行 分 别 计 算f(x0+δx0，y0) 和f(x0，y0+δy0)。此 过 程 称 为 一 次 迭 代。另外，需设置期望计算精度低于梯度的计算精度。

（2）优化结果分析

通过NLPQL 算法，得到最优解为：x=1.2，y=8.0。使用该最优解，得到响应变量MaxVelo=0.34 m/s，如图11 所示；溢流口开度如图12 所示，满足不大于0 的目标；约束FinalOutP=0.1 Bar，输出压力如图13 所示，由图可知，输出压力不再发生大幅度振动。

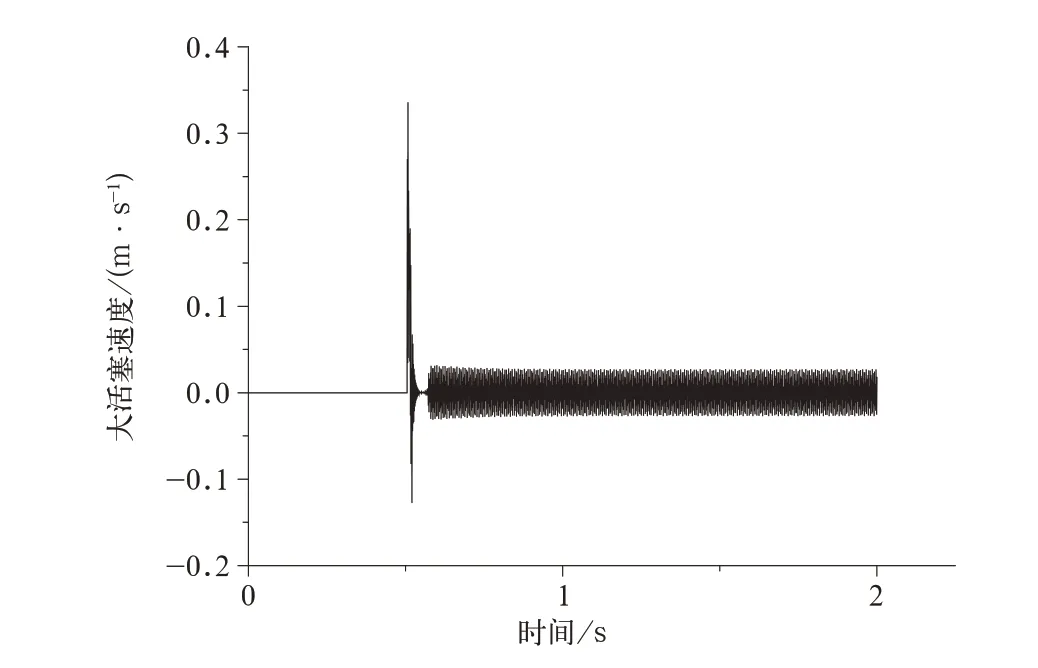
图11 大活塞速度

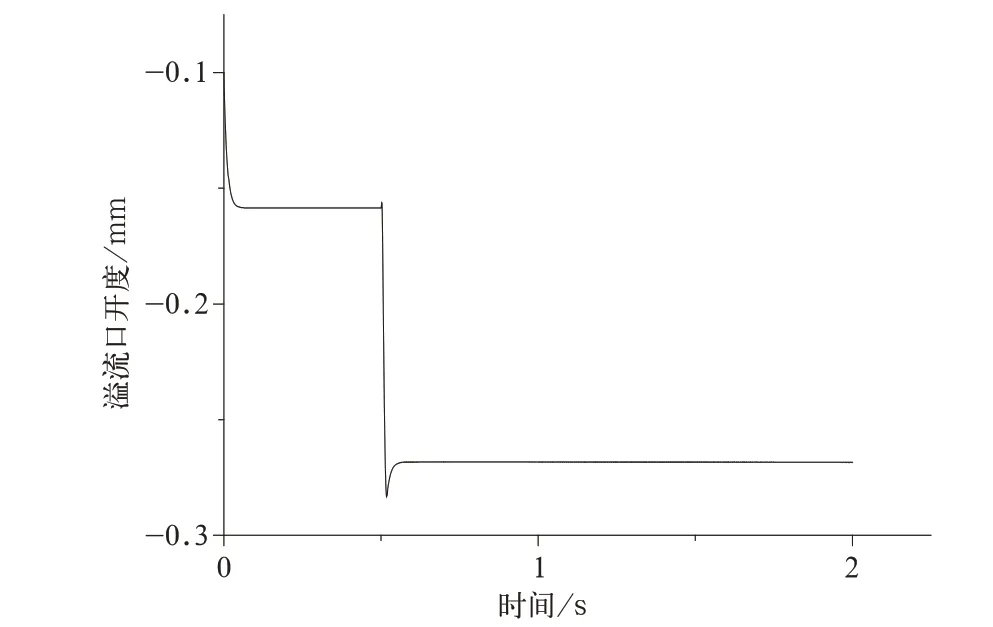
图12 溢流口开度

图13 出气口压力

3 验证不可控因子对模型的影响效应

不可控因子有输入压力pUp，调节弹簧刚度b。在上文最优模型基础上进行统计学分析。由于输入压力在800～950 kPa 之间，是随机分布的，文中在该压力范围，将输入压力近似为均匀分布，计算得到在该压力范围内大活塞最大速度频次分布直方图，如图14 所示。另外，观察最大溢流口开度响应变量，其值均为-0.1，符合预期优化目标。另外假设调节弹簧刚度的不确定性用高斯分布来建模，其平均值为65 500 N/m，标准方差为6 550 N/m（公称值的1%）。计算得到大活塞最大速度频次分布直方图如图15 所示。由图14、图15 可知，当输入压力在已知范围内，调节弹簧刚度符合一般高斯分布时，大活塞最大速度在较小范围内波动，且溢流口开度均符合目标要求。因此，本次试验设计寻找到的最优解既能满足响应变量的目标要求，又能控制不可控变量对响应变量的效应在允许值范围内。

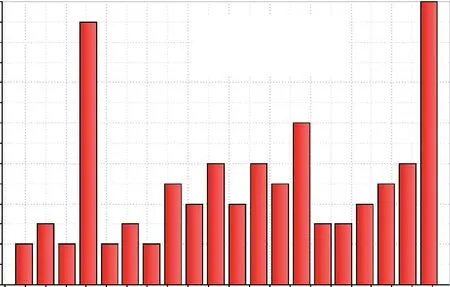
图14 大活塞最大速度频率分布直方图a

图15 大活塞最大速度频率分布直方图b

4 结 论

文中给出了一种高速列车制动产品优化设计的方法。以减压阀为对象，首先通过频谱分析确认减压阀噪声发生原因，确定优化目标。通过仿真建模，对制动系统减压阀的噪声原因进行单因子分析，找出对响应变量有较明显影响的因子。然后用全因子的试验设计方法，计算得到各因子的线性回归系数，对全10 个因子进行筛选，得到4 个对响应变量影响最明显的因子。并根据pareto 图直观计算出对响应变量的效应百分比。确定对响应变量影响效应最大的两因子反馈孔直径d，阀口通径Di为控制变量。通过NLPQL 优化算法进行基于目标和约束条件的控制变量寻优。应用最优控制变量建模，并对不可控因子进行统计研究，验证不可控因子对模型的响应变量效应在可接受范围内，试验设计目标完成。

文中验证了将试验设计方法应用于高速列车制动产品优化设计的可行性。此试验设计方法也可用于产品的故障分析，对高速列车制动系统的检修，寿命预测具有指导意义。