基于伯努利矩阵的音频信号观测矩阵设计与仿真*

喀什大学物理与电气工程学院 彭慧 娄颜超

压缩感知理论颠覆了传统的奈奎斯特采样定理,提出了一种将信号采样与压缩过程合二为一的信号采集方法。其采样于压缩过程实质是线性观测的过程。音频信号在压缩采样过程中要完成高维矩阵运算,利用传统的压缩感知观测矩阵如高斯随机矩阵、部分哈达玛矩阵对音频信号压缩采样的时间复杂度、空间复杂度较高,难以在计算、存储资源有限的硬件设备上实现。针对该问题,本文针对音频信号设计了一种以伯努利矩阵为基础的观测矩阵,并对该矩阵的观测性能及信号重建效果进行了仿真分析,分析表明该矩阵能以高概率满足RIP性质,且观测性能及重建效果与高斯随机矩阵相当,但大大节约了计算量和计算时间。

0 引言

压缩感知理论的出现为信号的采集与压缩提供了思路,如语音信号压缩感知[1-2]、牲畜音频信号分析[3]。与传统的先高速采样再压缩的处理方法不同,压缩感知理论提出将采样与压缩过程合二为一,在采样的同时进行压缩,压缩采样得到的是包含信号所有信号的少量数据。

目前压缩感知观测矩阵主要包含随机矩阵、部分正交矩阵、结构化矩阵三大类。最常用的观测矩阵是高斯随机矩阵、托普利兹矩阵、部分哈达玛矩阵等。

高斯随机矩阵的缺点是矩阵中的每一个元素都需要储存,需要占用较大的存储空间,因此在硬件上实现高斯随机观测较为困难。托普利兹(Toeplitz)矩阵和部分哈达玛矩阵减少了随机变元数量、简化了观测矩阵的结构,但仍然在一定程度上存在计算复杂度高和需要存储空间大的问题。

1 压缩感知理论下音频信号处理过程

Cands、Tao等人提出的压缩感知理论[4]指出,奈奎斯特采样定理是信号精确重建的充分条件而非必要条件。只要信号具有稀疏性或在某个变换域内具有稀疏性(即信号具有可压缩性),那么就可以以远低于奈奎斯特频率的速率对信号进行低速采样,低速采样值中包含了信号重建所需的全部信息。

音频信号在傅里叶变换、离散余弦变换、小波变换等变换下都具有稀疏性,满足压缩感知理论要求。基于压缩感知的音频信号处理有两种方案[5]。第一种方案,先将信号进行奈奎斯特采样,对采样后的信号进行压缩感知线性观测得到压缩值。第二种方案,直接对音频信号进行压缩采样,将采样与压缩过程合并。

Candes等人提出,为使K个稀疏系数能由M个观测值准确恢复,观测矩阵必须满足限制等距特性RIP(Restricted Isometric Property)[6],即对任意具有K稀疏度的矢量V,Θ都能保证(2-6)所示的不等式成立,式中0＜δ＜1。

RIP准则的等价条件说明:只要测量矩阵和稀疏矩阵不相干,信号也能够精确恢复,此时恢复矩阵能以高概率满足RIP准则。

2 音频信号观测矩阵设计

由于伯努利矩阵中的元素可能的取值少,而且可以以整数形式出现,所以在实际应用中可以减小计算量、节约存储空间。

伯努利类测量矩阵中,随机对称符号矩阵(Random Symmetric Signs Matrices)[7]是最常用的。若有随机对称符号矩阵Φ,且 Φ ∈ Rm×n。

那么矩阵中的每一个元素都独立的服从对称符号伯努利分布,如式(2)所示。

伯努利二进制矩阵中零元素的存在给线性观测过程带来的影响可以这样来理解:如果对称符号矩阵能够将信号中的信息全部传递至观测值向量中,那么伯努利二进制矩阵中的元素有1/2的可能性为零,导致了信号中的信息有1/2不能传递到伯努利二进制矩阵所得到的观测值中。但是,值得注意的是,观测值向量中若有m个元素,那么伯努利二进制矩阵所得到的观测值向量能够以的概率得到信号中的全部信息,因为ΓΦ满足RIP准则,即ΓΦ的元素完好地采集到了x中的信息,与ΓΦ所对应的αΦ以概率 满足信号的精确重建,随着m的增大,该概率趋向于1。

3 仿真与分析

仿真中选取了音乐信号为研究对象,格式为WAV,将截取2s～5s的信号进行压缩观测并重建。选取DCT基作为信号的稀疏基,OMP[8]算法作为信号重建算法。

3.1 观测矩阵性能分析

将一段时长为3S的音频信号进行分段处理,分段长度取N=512;与常用观测矩阵,高斯随机矩阵、托普利兹、部分哈达玛矩阵的结果进行比较,结果为40段相同长度的信号,且每段信号仿真100次后得到的平均值,对比结果如图1所示。

图1中结果表明随着观测点数的增加,信号的重建信噪比提高,重建效果更好。在相同的观测点数下,高斯随机矩阵和伯努利二进制矩阵观测效果相当,都优于托普利兹矩阵和部分哈达玛矩阵。

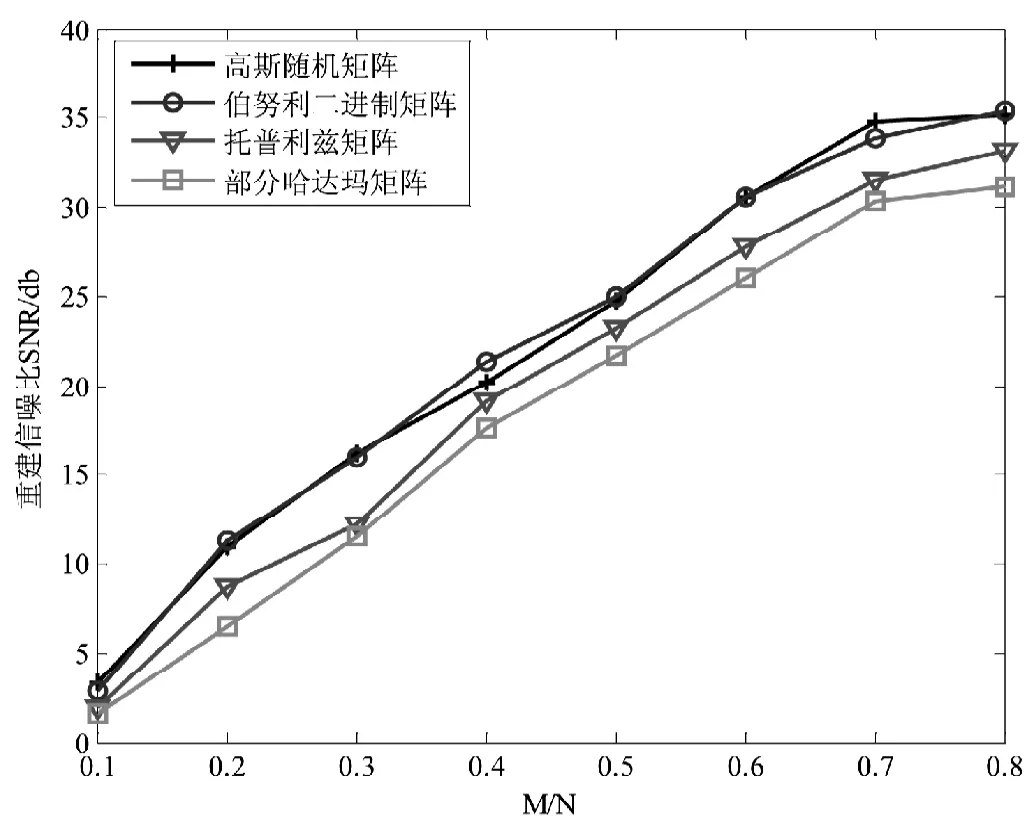
图1 四种观测矩阵重建效果对比Fig.1 Comparison of the reconstruction effects of the four observation matrices

为进一步验证音频信号分段长度不同对信号观测与重建效果的影响,取一段长度为3s的测试信号,对信号进行不同长度的分段处理。表1还列出了仿真过程中所需的运算时间。结果表明当信号分段长度越长,处理相同长度的音频信号所需的时间越长。这是由于分段长度越长,矩阵维数越高,运算的复杂度越大。但分段长度越长信号的重建信噪比越高,重建效果越好。所以在观测过程中要综合考虑计算复杂度与重建效果两方面,针对信号特点选择合适的信号分段长度。

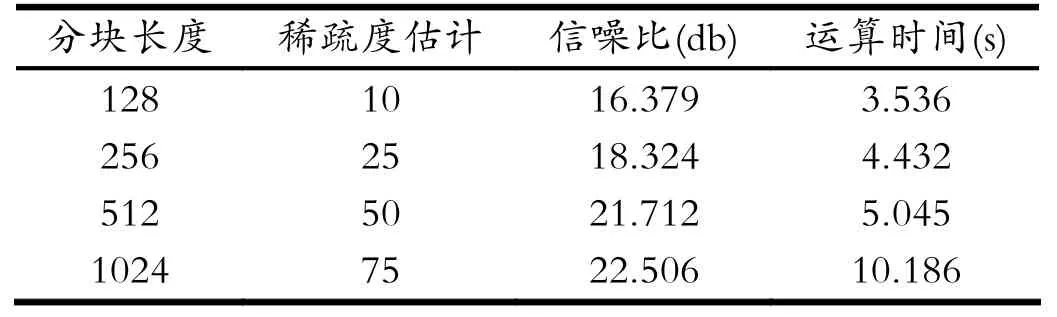
表1 信号分块长度与稀疏度估计、重建信噪比、运算时间的关系Tab.1 The relationship between the signal block length and sparsity estimation, reconstruction signal-to-noise ratio, and computing time

3.2 噪声性能分析

仿真中噪声为高斯白噪声,在原始音频信号中加入不同信噪比的高斯白噪声,对比在高斯随机矩阵、二进制伯努利矩阵、托普利兹矩阵、部分哈达玛矩阵观测下,信号的重建效果,重建效果用重建信噪比来衡量。结果如表1所示。

从表2中结果可以看出:当含噪信号的信噪比为5db至25db时,四种观测矩阵观测下得到的重建信噪比均高于原信号信噪比,这就说明,压缩感知对含噪信号具有一定的信号增强功能。当含噪信号的信噪比为25db时托普利兹矩阵和部分哈达玛矩阵的重建信噪比低于25db,高斯随机矩阵和伯努利二进制矩阵的重建信噪比仍然高于25db,这就说明,托普利兹矩阵和部分哈达玛矩阵对音频信号的观测性能不如高斯随机矩阵和伯努利二进制矩阵。

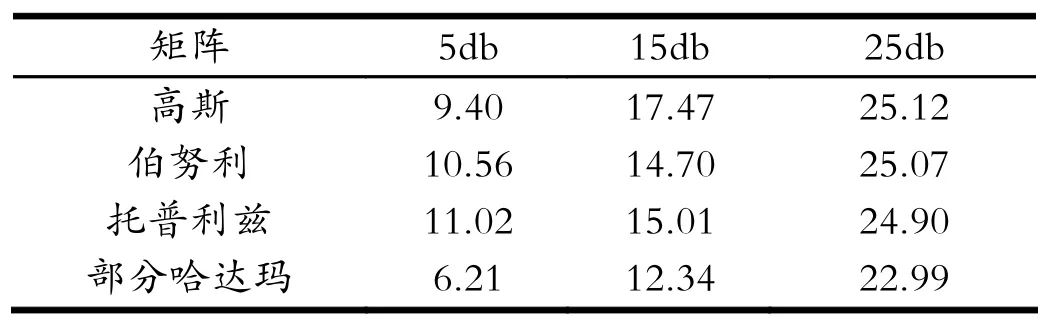
表2 信号中加入不同强度噪声时四种观测矩阵性能对比Tab.2 Comparison of the performance of the four observation matrices when different intensities of noise are added to the signal

4 结语

本文基于伯努利矩阵,结合随机对称符号矩阵以高概率满足RIP准则的特点,针对音频信号设计了伯努利二进制观测矩阵。仿真实验表明,伯努利二进制矩阵在信号不含噪声情况下,观测性能与高斯随机矩阵相当,但由于其矩阵元素不是1就是0,大降低了观测矩阵生成及观测过程的计算复杂度。在含噪声情况下,观测过程具有信号增强功能。本文提出矩观测矩阵为压缩感知在计算机存储资源有限的硬件上实现提供了可行性方案。

引用

[1] 钱永青.基于压缩感知的语音加密[J].电子测量技术,2020,42(2):139-142.

[2] 马春,汪庆,李亚.基于改进Kalman滤波l1模加速算法的语音信号重构[J].西华大学学报(自然科学版),2021(4):27-34.

[3] 吴亚文,赵家龙,侯金波,等.基于改进压缩感知的生猪音频信号处理[J].江苏农业科学,2020,48(10):250-255.

[4] D.Donoho.Compressed Sensing[J].IEEE Transactions on Information Theory,2006,52(4):1289-1306.

[5] 彭慧.压缩感知在物联网系统中的应用研究[J].机电信息,2020(23):93-94.

[6] E.Candes.The Restricted Isometry Property and Its Implications for Compressed Sensing[J].Comptes Rendus Mathematique,2008,346:589-592.

[7] R.Baraniuk,M.Davenport,R.Devore,etal.A Simple Proof of the Restricted Isometry Property for Random Matrices[J].Constructive Approximation,2008,28(3):253-263.

[8] 张蒙,王海斌,汪俊,等.基于动态阈值匹配追踪的主动声呐直达波抑制方法[J].应用声学,2020,39(5):661-669．