创新系统主体间协同关系对绿色创新效率影响的实证分析

2021-11-18吕岩威

中国科技论坛 2021年11期

吕岩威，刘洋，杨菲

(山东大学商学院，山东威海 264209)

0 引言

随着知识和技术更新速度的加快，当代创新模式已演变为以创新系统内多元主体协同互动为基础的协同创新模式[1]。在创新系统内，企业、高校、科研机构是创新的直接主体，政府和金融机构作为间接主体参与创新[2]。创新系统各主体通过思想、知识、技术和机会的共享，可以创造跨越企业边界的创新，进而提升企业创新力量[3]。近年来，中国政府出台了一系列政策推进创新系统主体间协同创新。根据《全球竞争力报告》显示，中国产学研协同创新能力已由2012—2013年度的第35位，上升到2017—2018年度的第28位，反映出企业从依托内部力量向借助外部资源进行创新的转变。然而，创新系统各主体在协同创新过程中仍然面临诸多问题，如协同创新体制机制滞后、利益分配机制不健全、信息不对称、价值取向不一致、合作方式过于单一等，导致创新系统主体间难以有效协同。在此背景下，分析创新系统主体间协同关系对绿色创新效率的影响，具有重要的理论价值和现实意义。

鉴于此，本文基于2006—2017年省级面板数据，运用DEA-Tobit模型和分位数回归模型分析创新系统主体间协同关系对绿色创新效率及其条件分布的影响，构建面板向量自回归 (PVAR)模型并利用脉冲响应函数探讨创新系统主体间协同关系对绿色创新效率的动态冲击影响，基于方差分解方法分析创新系统主体间协同关系影响绿色创新效率结构冲击的贡献度，以期从协同创新的视角揭示促进我国区域绿色创新效率提升的关键影响因素。

1 文献综述

已有研究一方面是从微观企业层面研究创新系统主体间协同与创新绩效之间的关系。Ketchen 等[3]发现合作创业能使小企业保持创造力和灵活性，而协同创新有利于大企业在现有领域之外寻找机会。解学梅[4]发现企业与企业、企业与中介、企业与研究机构的协同创新网络促进中小企业创新绩效提升，但企业与政府的协同创新网络影响不显著。Marchi[5]发现绿色创新中与外部企业的合作非常重要，环境创新型企业与外部合作伙伴在创新方面的合作程度远高于其他创新型企业。吴悦等[6]发现企业通过协同创新产业链，促进科技成果转化，提升企业创新水平。胡宝贵等[7]发现创新系统各主体在协同创新过程中普遍存在效率不高、效果不理想的情况，政府对推进协同创新具有重要作用。康益敏等[8]发现伙伴关系促进企业创新绩效提升，而协同创新为其传导渠道。另一方面是从宏观区域层面进行研究。Fritsch等[9]发现私营部门与公共研究机构之间的研发互动强度促进研发效率提升。贺灵等[10]发现创新网络要素间协同对地区创新绩效均具有显著促进作用，且创新网络所处的硬环境和软环境对地区创新绩效也具有显著正向影响。Broekel[11]发现研发合作补贴是刺激区域创新效率的合适政策措施，创新能力较低的地区从区域企业之间的研发合作和与非区域公共研究机构的研发合作补贴中获益最大。而对创新能力较强的地区来说，从非区域大学的研发合作补贴中获益最大。白俊红等[2]发现政府资助、产学合作、产研合作促进创新绩效提升，但金融机构资助具有抑制作用。刘友金等[12]发现政府支持、企业内部协同、科研机构内部协同均对地区创新绩效产生显著的、较大的促进作用，但产学研全面协同、高校内部协同对地区创新绩效影响较弱，协同效果不理想。蒋兴华等[13]发现协同意愿、伙伴关系对创新绩效具有显著正向影响，而政府支持促进协同意愿、伙伴关系，起调节作用。

综上，已有研究为本文提供了重要启示，但也存在有待拓展之处：①已有研究主要集中在创新系统主体间协同机理、运行机制、演化博弈与协同能力评价等方面，而就创新系统主体间协同关系对区域创新绩效影响的探讨则相对欠缺。事实上，创新系统各主体具有不同的战略目标，各主体对合作所产生的效益会有不同的预期[14]，如何通过政策引导和制度安排，调动创新系统各主体的积极性，进而促进创新绩效提升，目前还缺少相关的研究。②少数相关定量研究文献均忽略了在创新水平不同的地区，创新系统主体间协同关系对创新绩效的影响也可能存在差异，且均未采用面板向量自回归 (PVAR)模型探讨创新系统主体间协同关系对创新绩效的动态冲击效应、贡献度及其区域异质性。

2 模型与变量

2.1 模型构建

(1)DEA-Tobit模型。为了精确测算绿色创新效率，并进一步分析其影响因素，借鉴已有研究采用 “DEA-Tobit两步法”进行分析[15-17]。第一步先利用SBM-DEA模型测算绿色创新效率值，第二步构建Tobit模型分析创新系统主体间协同关系对绿色创新效率的影响。

①SBM-DEA模型。SBM-DEA模型由Tone[18]首次提出，假设生产系统有n个决策单元 (DMU)，每个DMU都有投入X、期望产出Yg和非期望产出Yb这3个元素，并且x∈Rm，yg∈RS1，yb∈RS2，定义矩阵X，Yg，Yb为：

X=[x1,...,xn]∈Rm×n

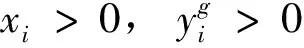
SBM-DEA模型可表示为：

(1)

式中，s-为投入松弛量，sg为期望产出松弛量，sb为非期望产出松弛量，λ为权重向量，ρ为目标函数，且0≤ρ≤1。当ρ=1时，DMU是有效率的；ρ<1，DMU存在冗余，需要优化配置。

②Tobit模型。通过SBM-DEA模型测算出的绿色创新效率值是0～1的截断数据，若使用普通最小二乘法进行回归，其参数估计值可能会出现有偏和非一致性。为了解决这一问题，Tobin[19]首次提出截断回归模型即 Tobit模型，并指出对于受限被解释变量，遵循最大似然估计 (MLE)的Tobit模型是较好选择，Tobit模型可表示为：

(2)

当yi=0时，其概率密度函数表示为：

(3)

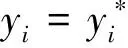
(4)

(2)分位数回归模型。为了避免基于均值回归而导致的估计偏误，采用分位数回归方法探讨创新系统主体间协同关系对绿色创新效率条件分布的影响规律。分位数估计理论由Koenker等[20]首次提出，该方法基于被解释变量y的条件分布来拟合解释变量x，对异常值的敏感度相较于均值回归更小，估计结果也更稳健。

设随机变量Y的分布函数为F(y)=P(Y≤y)，则y的τ分位数函数定义为：

Q(τ)=inf{y：F(y)≥τ}

(5)

式中，τ为回归线以下数据占全部数据比重，0<τ<1。y的分布被τ分成小于Q(τ)、大于Q(τ)两个部分。为了求解回归模型，首先定义概率密度函数ρτ(μ)为：

(6)

式中，μ为概率密度函数的参数，ρτ(μ)为y的样本点处在τ分位之下和之上时概率密度函数关系。分位数模型表示为：

(7)

寻求y在Q分位数下的最小离差和，可表示为：

(8)

(9)

由此，当τ在 (0，1)区间取不同数值时，便可得到不同参数估计值。

(3)面板向量自回归 (PVAR)模型。为了揭示创新系统主体间协同关系对绿色创新效率的动态冲击，通过PVAR模型的脉冲响应函数分析创新系统主体间协同关系变量变动对绿色创新效率带来的冲击反应，并运用方差分解方法分析创新系统主体间协同关系变量对绿色创新效率变化的贡献度。PVAR模型由Holtz-Eakin等[21]首次提出，可表示为：

(10)

式中，yi,t为k维变量向量，i为省份，t为时间，β0为截距项，βj为回归的系数矩阵，p为变量滞后阶数，ηi为个体效应向量，γt为时间效应向量，εi,t为随机扰动项。

2.2 变量与数据

被解释变量：绿色创新效率 (IE)。采用SBM-DEA模型测度2006—2017年中国各省份绿色创新效率。其中，创新投入指标采用R&D人员全时当量、R&D资本存量表征，创新期望产出指标采用技术市场成交额、新产品销售收入表征，非期望产出采用工业废水排放量、工业废气排放量和银行不良贷款率表征[22-23]。

核心解释变量：创新系统主体间的协同关系。基于数据可得性考虑，从资金角度表征创新系统主体间协同关系。其中，以R&D经费内部支出中政府资金、银行贷款的比重分别衡量政府资助 (gov)、金融支持 (fin)，表征创新系统间接主体对直接主体的资助力度。以高校和研发机构R&D经费内部支出中企业资金的比重衡量产学研合作 (iur)，表征创新系统直接主体之间的资金往来。

控制变量：国内知识技术转移度 (tdd)、国外知识技术转移度 (tdf)、外商直接投资 (fdi)。其中，tdd采用国内技术市场技术流向地域合同金额占地区生产总值的比重表征，tdf采用国外技术引进合同金额占地区生产总值的比重表征，fdi采用外商直接投资额占地区生产总值的比重表征。

以中国内地30个省份为研究对象 (不含西藏)，数据来自历年《中国统计年鉴》《中国科技统计年鉴》《中国环境统计年鉴》《中国金融统计年鉴》及各地统计年鉴，描述性统计结果见表1。

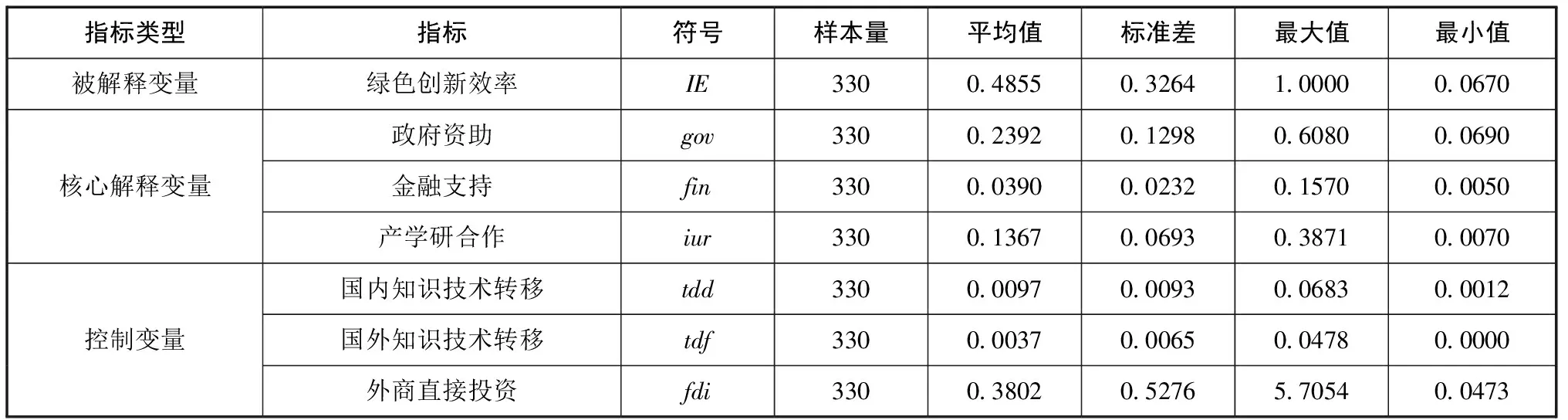
表1 数据的描述性统计

3 创新系统主体间协同关系对绿色创新效率的静态影响

3.1 面板单位根检验

为了保证回归结果的稳定性，选取相同根检验中的LLC检验、不同根检验中的ADF-Fisher和PP-Fisher检验方法进行面板单位根检验，结果见表2。由表2可知，所有变量的原序列均平稳，可以构造计量模型进行分析。

3.2 Tobit回归结果分析

利用中国省级面板数据，按照全国总体、东部、中部、西部地区分组，采用Tobit 模型对式 (2)进行回归，以检验创新系统主体间协同关系对绿色创新效率的影响，回归结果见表3。由表3可知，政府资助对全国总体及东部、中部和西部地区绿色创新效率均有负向影响，且在全国总体、东部和中部地区均通过了至少5%的显著性水平检验，但在西部地区不显著。金融支持对全国总体及东部、中部和西部地区绿色创新效率也均有负向影响，且在全国总体通过了5%的显著性水平检验，但在东部、中部和西部地区不显著。产学研合作对全国总体及东部、中部和西部地区绿色创新效率均有正向影响，且在全国总体、东部和西部地区均通过了至少5%的显著性水平检验，但在中部地区不显著。这说明在创新系统各主体之间的协同关系中，间接主体与直接主体之间的协同关系 (政府资助、金融支持)对各地区绿色创新效率产生了抑制作用，而直接主体之间的协同关系 (产学研合作)则促进了各地区绿色创新效率提升。

表3 Tobit回归结果

3.3 分位数回归结果分析

Tobit 模型仅能解释创新系统主体间协同关系对绿色创新效率条件均值的影响，存在一定的局限性，因此采用分位数回归模型估计创新系统主体间协同关系对绿色创新效率在25%、50%、75%这3个分位点的影响变化情况，回归结果见表4。

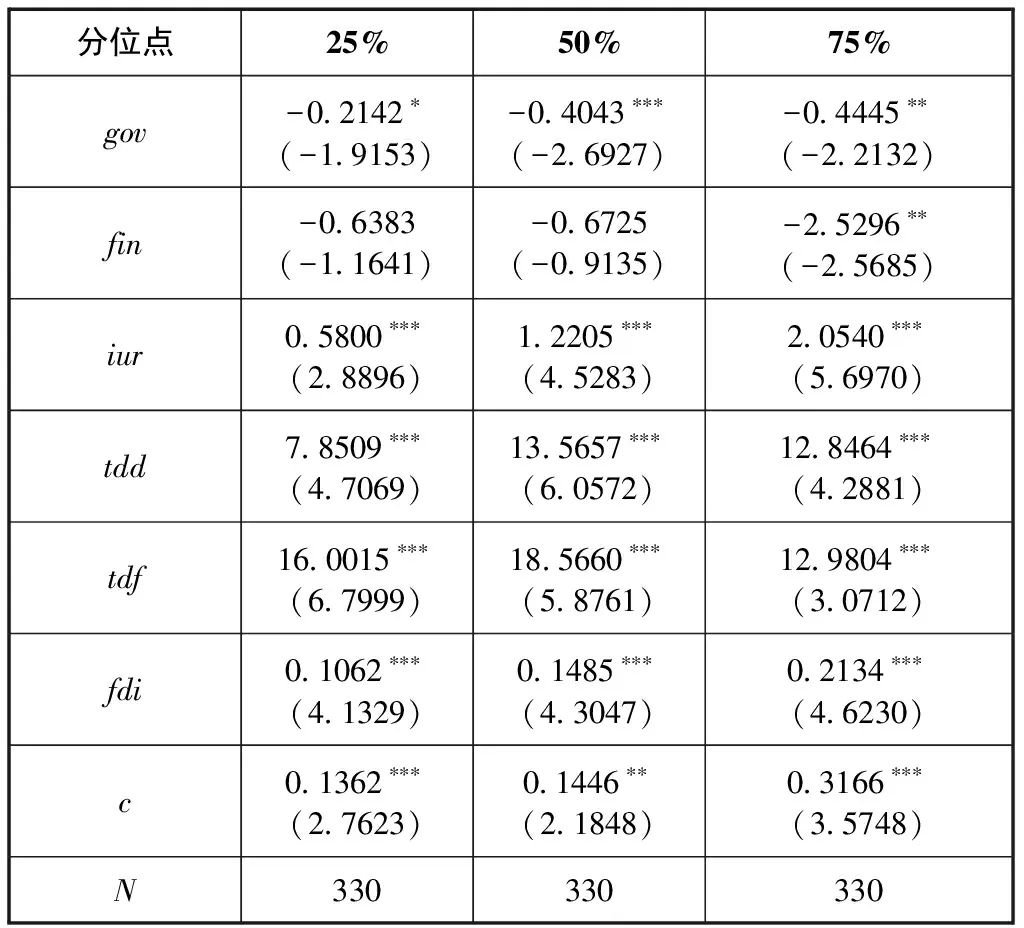
表4 分位数回归结果

(1)政府资助在25%、50%、75%分位点处的系数分别为-0.2142、-0.4043、-0.4445，且均在至少10%的显著性水平上显著为负。这说明，一方面政府资助对研发投入的挤出效应、政企之间信息不对称和企业寻租行为等导致政府资助对各分位点绿色创新效率均有显著抑制作用；另一方面，从25%分位点到75%分位点，政府资助系数的绝对值增大，说明在绿色创新效率较高的地区，政府资助对研发投入的挤出效应更大，对绿色创新效率的抑制作用就高于低分点位。

(2)金融支持在25%、50%、75%分位点处的系数分别为-0.6383、-0.6725、-2.5296，但只在75%分位点的系数以5%的显著性水平显著为负，在其余分位点的系数均不显著。这说明，一方面金融机构对企业贷款存在的 “所有制歧视”和 “规模歧视”，导致了金融错配问题，使得金融支持对各分位点绿色创新效率均具有抑制作用；另一方面，从25%分位点到75%分位点，金融支持系数的绝对值在增大，说明在绿色创新效率较高的地区，中小企业的研发活动更加活跃，金融支持的负向影响也更大。

(3)产学研合作在25%、50%、75%分位点处的系数分别为0.5800、1.2205、2.0540，且均在1%的显著性水平上显著为正。这说明，一方面产学研合作不仅实现了技术协同效应，还促进了知识、技术的共享，进而对各分位点绿色创新效率均具有正向作用；另一方面，从25%分位点到75%分位点，产学研合作系数的绝对值在增大，说明绿色创新效率越高的地区创新环境越好，越有利于高校、科研机构与企业之间的合作创新，对绿色创新效率的促进作用也就越大。

4 创新系统主体间协同关系对绿色创新效率的动态冲击

4.1 最优滞后阶数的选取

进一步运用PVAR模型分析创新系统主体间协同关系对绿色创新效率的动态冲击。为避免模型中时间效应和个体效应造成估计偏误，首先用均值差分法消除时间效应，而后用一阶向前差分法消除个体效应。对于滞后阶数选取，综合考虑AIC (Akaike Information Criterion)、BIC (Bayesian Information Criterion)以及HQIC (Hannan-Quinn Information Criterion)准则以及PVAR模型的收敛趋势，确定全国总体及东部、中部和西部地区的最优滞后阶数分别为4、2、2和2阶，结果见表5。

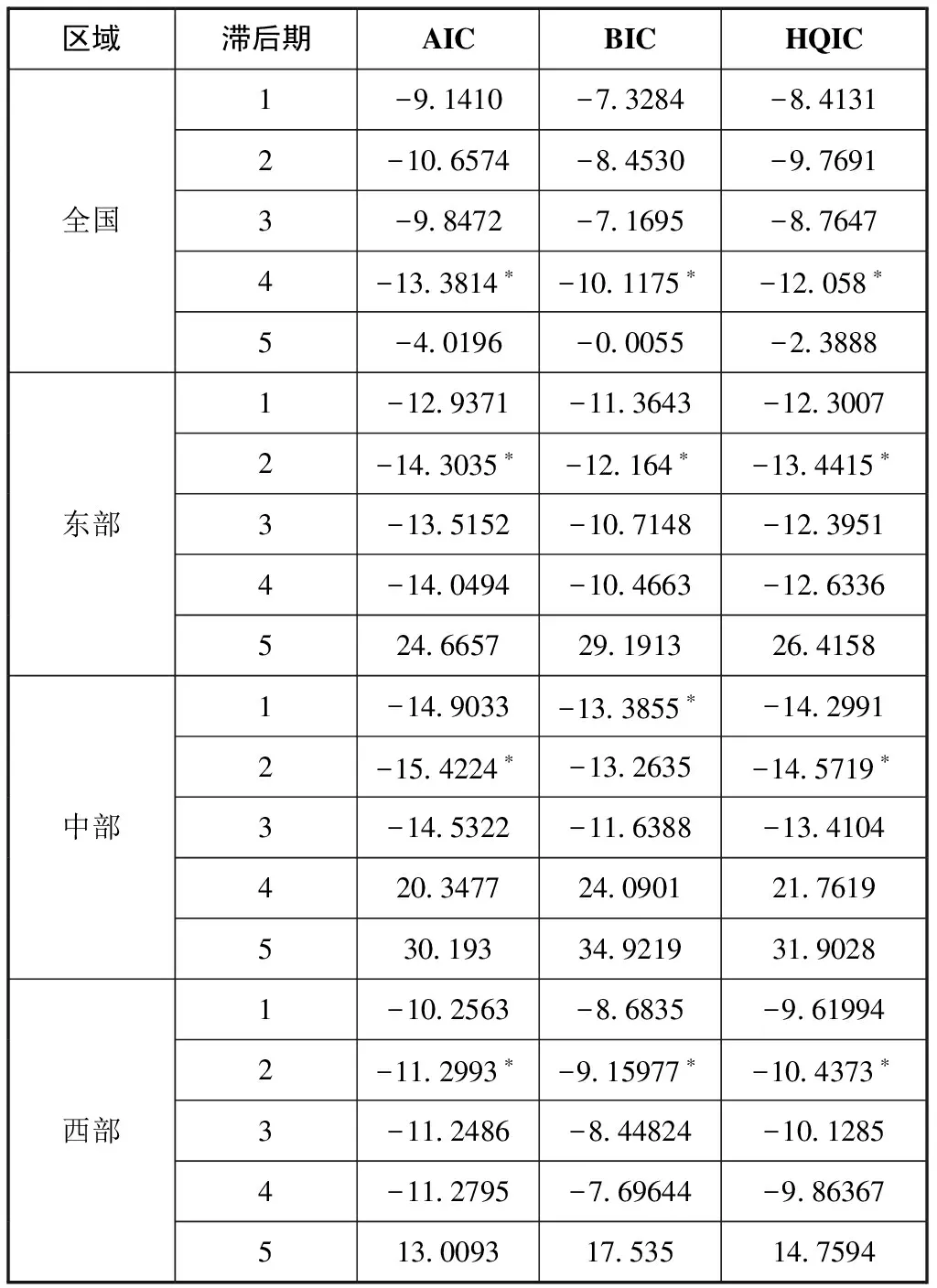
表5 最优滞后阶数的选取

4.2 脉冲响应分析

脉冲响应函数刻画变量间动态交互效应和时滞关系。借助Stata16软件，通过蒙特卡洛 (Monte Carlo)实验模拟 500次，分析全国总体及东部、中部和西部地区创新系统主体间协同关系各变量加上一个标准差大小的冲击对绿色创新效率当前和未来值的影响。变量顺序为IE、gov、fin、iur，PVAR模型的脉冲响应估计结果见表6，脉冲响应如图1所示，图1中的横轴为冲击作用的响应期数，纵轴为绿色创新效率对创新系统主体间协同关系各变量的响应大小，由表6和图1可以得出以下结论。

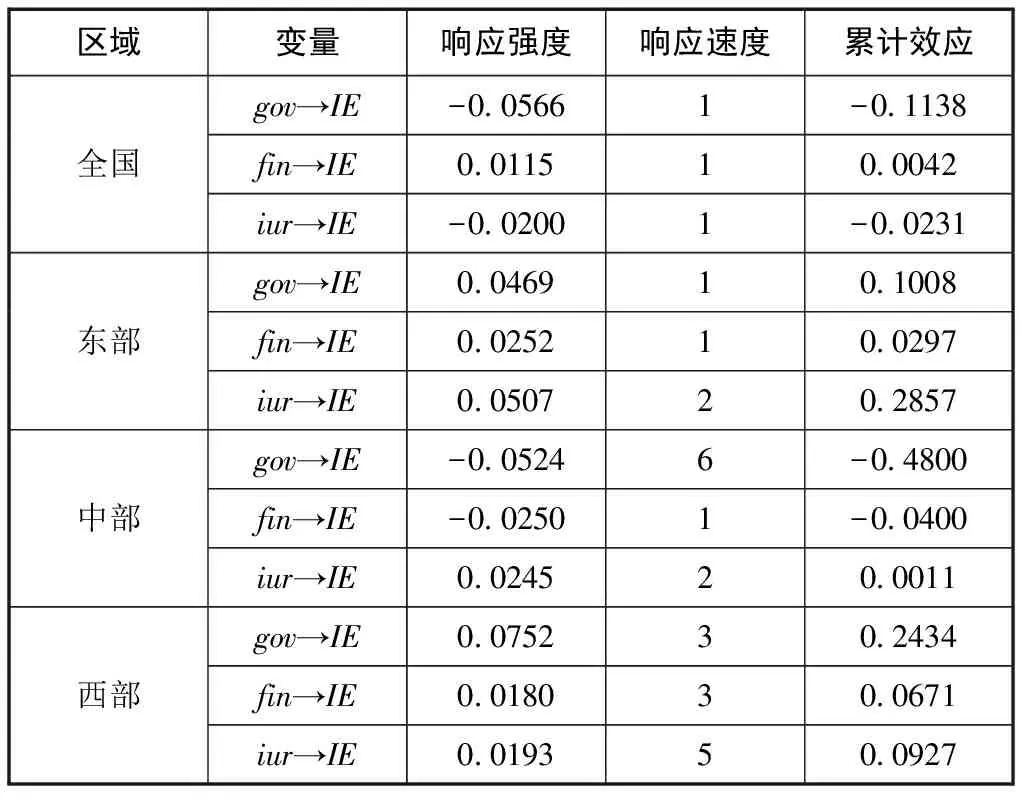
表6 绿色创新效率对创新系统主体间协同关系的脉冲响应估计结果

(1)绿色创新效率对创新系统主体间协同关系各变量的冲击在响应强度和响应速度上均存在较大区域差异。对于政府资助的一个正交化冲击，全国总体及东部、中部和西部地区绿色创新效率的响应峰值分别是-0.0566、0.0469、-0.0524、0.0752，响应峰值分别在第1期、第1期、第6期和第4期。对于金融支持的一个正交化冲击，全国总体及东部、中部和西部地区绿色创新效率的响应峰值分别是0.0115、0.0252、-0.0250、0.0180，响应峰值分别在第1期、第1期、第1期和第3期。对于产学研合作的一个正交化冲击，全国总体及东部、中部和西部地区绿色创新效率的响应峰值分别是-0.0200、0.0507、0.0245、0.0193，响应峰值分别在第1期、第2期、第2期和第5期。

从响应强度看，东部地区绿色创新效率对金融支持和产学研合作冲击的响应强度最大，但对政府资助冲击的响应强度相对较小；中部地区绿色创新效率对政府资助、金融支持和产学研合作冲击的响应强度均较大；西部地区绿色创新效率对政府资助冲击的响应强度最大，但对金融支持和产学研合作冲击的响应强度相对较小。从响应速度看，东部地区绿色创新效率对政府资助的响应速度最快，中部最慢；东部和中部地区绿色创新效率对金融支持、产学研合作的响应速度最快，西部最慢。

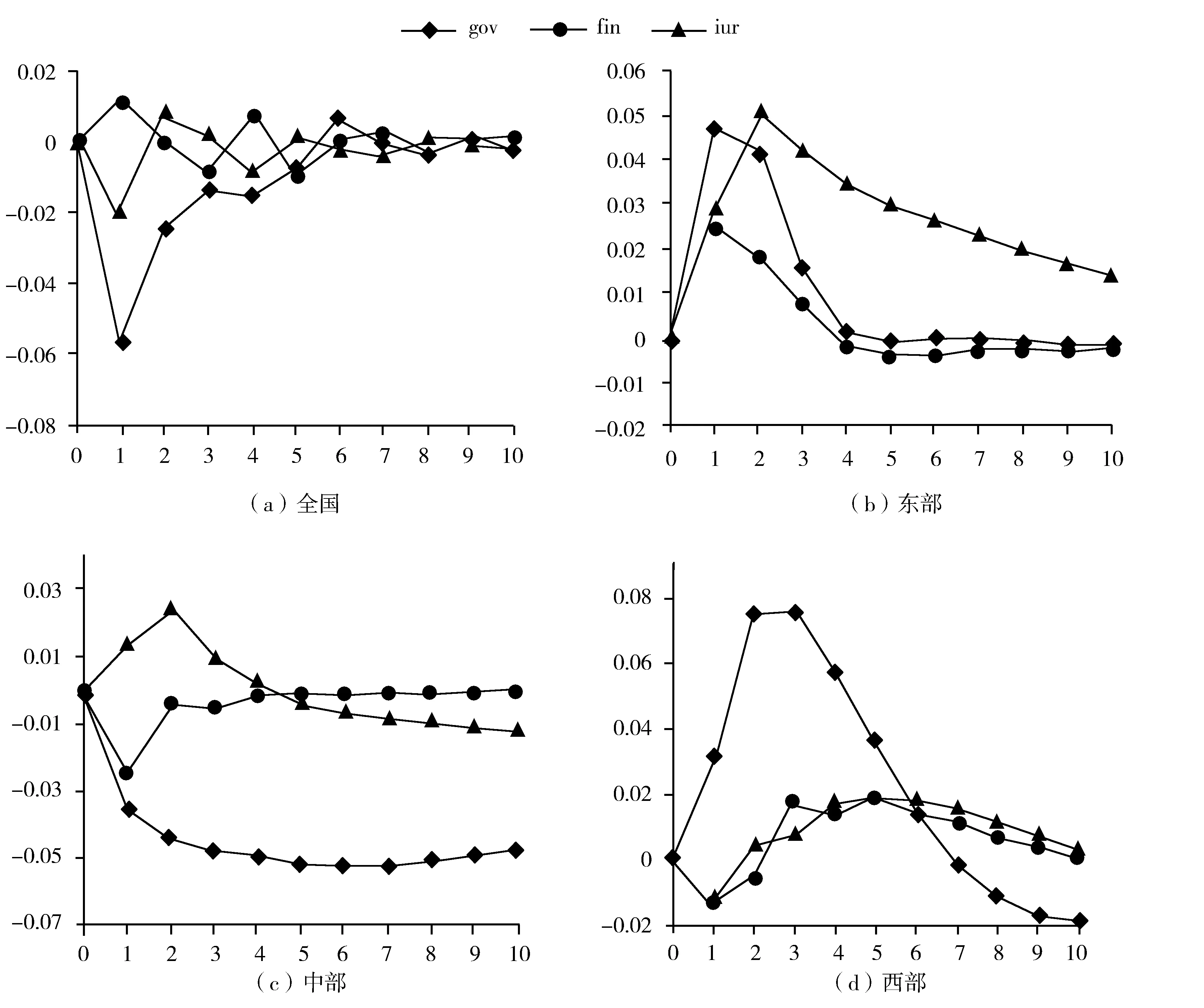
图1 绿色创新效率对创新系统主体间协同关系的脉冲响应

(2)绿色创新效率对创新系统主体间协同关系各变量冲击的累积效应存在较大的区域差异。政府资助对全国总体及东部、中部和西部地区绿色创新效率冲击的累积效应分别为-0.1138、0.1008、-0.4800、0.2434。可见，政府资助对西部地区绿色创新效率冲击的累积效应最大，说明政府资助缓解了西部地区研发经费不足的现状，有助于激励企业的技术创新活动，但对中部地区绿色创新效率冲击的累积效应为负，这说明政府资助对中部地区创新投入产生了挤出效应，抑制了绿色创新效率提升。

金融支持对全国总体及东部、中部和西部地区绿色创新效率冲击的累积效应分别为0.0042、0.0297、-0.0400、0.0671。可见，金融支持对东部地区绿色创新效率冲击的累积效应最大，说明东部地区金融市场化程度较高，而金融市场化有助于改善外部融资环境，提升绿色创新效率。金融支持对中部地区绿色创新效率冲击的累积效应为负，说明 “所有制歧视”和 “规模歧视”所导致的金融错配问题在中部地区尤为严重。

产学研合作对全国总体及东部、中部和西部地区绿色创新效率冲击的累积效应分别为 -0.0231、0.2857、0.0011、0.0927。可见，产学研合作对东部、中部和西部地区绿色创新效率冲击的累积效应均为正，其中对东部地区绿色创新效率冲击的累积效应最大，说明东部地区优质高校和科研机构数量多，产学研合作更为高效，有利于绿色创新效率提升。产学研合作对全国总体绿色创新效率冲击的累积效应略小于0，说明绿色创新效率对产学研合作的动态响应存在区域异质性，产学研合作对绿色创新效率冲击的累积效应并非在所有省份都为正，在部分省份也可能表现为负。

(3)绿色创新效率对创新系统主体间协同关系各变量的冲击响应在各地区均表现为收敛趋势，但收敛的速度和轨迹不甚相同。在全国总体，绿色创新效率对政府资助的冲击响应表现为在第1期达到负的响应峰值后以较快的速度向零值收敛；绿色创新效率对金融支持的冲击响应表现为在第1期达到正的响应峰值后逐渐下降为负，并最终趋于零值附近；绿色创新效率对产学研合作的冲击响应表现为在第1期达到负的响应峰值后逐渐上升为正，并最终趋于零值附近。

在东部地区，绿色创新效率对政府资助的冲击响应表现为在第1期达到正的响应峰值后以较快的速度向零值收敛；绿色创新效率对金融支持的冲击响应表现为在第1期达到正的响应峰值后以较快的速度向零值收敛；绿色创新效率对产学研合作的冲击响应表现为在第2期达到正的响应峰值后逐渐向零值收敛。

在中部地区，绿色创新效率对政府资助的冲击响应表现为在第6期达到负的响应峰值后逐渐向零值收敛，但收敛速度很慢。绿色创新效率对金融支持的冲击响应表现为在第1期达到负的响应峰值后以较快的速度向零值收敛；绿色创新效率对产学研合作的冲击响应表现为在第2期达到正的响应峰值后逐渐向零值收敛。

在西部地区，绿色创新效率对政府资助的冲击响应表现为在第3期达到正的响应峰值后逐渐向零值收敛；绿色创新效率对金融支持的冲击响应表现为先降后升，在第3期达到正的响应峰值后逐渐向零值收敛；绿色创新效率对产学研合作的冲击响应表现为先降后升，在第5期达到正的响应峰值后逐渐向零值收敛。

4.3 方差分解分析

方差分解反映了对PVAR模型中内生变量产生冲击的每个随机扰动的相对重要性，进而度量结构冲击对内生变量变化的贡献度大小。为了分析创新系统主体间协同关系各变量对绿色创新效率变化的贡献度，进一步进行方差分解分析，结果见表7，由表7可以得出如下结论。

(1)无论是全国总体还是东部、中部和西部地区，绿色创新效率在滞后20期内受到自身前期积累的影响均为最大。但随着滞后时期的推移，绿色创新效率受到自身前期积累的影响均在逐渐减小，创新系统主体间协同关系各变量对绿色创新效率的影响越来越大。

表7 绿色创新效率对创新系统主体间协同关系动态响应的方差分解结果

(2)全国总体的政府资助、金融支持对绿色创新效率的贡献度呈现增加趋势，产学研合作对绿色创新效率的贡献度较为稳定。在滞后20期，政府资助、金融支持、产学研合作对绿色创新效率的贡献度分别达到13.7%、1.1%和1.8%，相比于金融支持和产学研合作，政府资助对全国总体绿色创新效率的影响更大。

(3)东部地区的政府资助对绿色创新效率的贡献度呈现下降趋势，金融支持对绿色创新效率的贡献度较为稳定，产学研合作对绿色创新效率的贡献度呈现增加趋势。在滞后20期，政府资助、金融支持、产学研合作对绿色创新效率的贡献度分别达到9.3%、2.5%和21.8%，相比于政府资助和金融支持，产学研合作对东部地区绿色创新效率的影响更大。

(4)中部地区的政府资助、产学研合作对绿色创新效率的贡献度呈现增加趋势，金融支持对绿色创新效率的贡献度呈现下降趋势。在滞后20期，政府资助、金融支持、产学研合作对绿色创新效率的贡献度分别达到46.5%、0.9%和3.2%，相比于金融支持和产学研合作，政府资助对中部地区绿色创新效率的影响更大。

(5)西部地区的政府资助、金融支持、产学研合作对绿色创新效率的贡献度均呈现增加趋势。在滞后20期，政府资助、金融支持、产学研合作对绿色创新效率的贡献度分别达到34.7%、2.8%和3.3%。相比于金融支持和产学研合作，政府资助对西部地区绿色创新效率的影响更大。