基于LDTW 的动态时间规整改进算法

夏寒松，张力生，桑春艳

（重庆邮电大学软件工程学院，重庆 400065）

0 概述

时间序列是指按照采集时间先后顺序排列的观测数据，广泛存在于金融［1-2］、道路交通［3］、社交网络［4-5］、工业电网［6］等领域。随着信息技术的发展，时间序列数据量与日俱增，利用相应数据挖掘技术从海量时间序列中发现潜在知识和规律已成为当前数据挖掘的研究热点。时间序列相似性度量是衡量两条时间序列相似程度的度量方法，是时间序列聚类和分类分析中不可缺少的步骤［7］，度量方法性能直接影响时间序列数据挖掘的效果［8］。

BERNDT 等［9］于1994 年提出的动态时 间规整（Dynamic Time Warping，DTW）是时间序列相似性度量中的常用方法。与传统相似性度量（如欧氏距离）相比，DTW 对时间序列的相位偏移、振幅变化等情况具有更强的鲁棒性。然而，DTW 算法存在“病态对齐”的缺陷，即在并不相似的特征之间进行对齐，使一条时间序列上的点匹配另一条时间序列上一大块区域的点［10］。在这种不合理匹配的情况下，可能出现同类时间序列之间的距离值大于不同类时间序列之间的距离值，进而影响最终的度量效果。

为了抑制病态对齐现象，提高时间序列之间的相似性度量效果，ZHANG 等［11］提出限制对齐路径长度的动态时间规整（LDTW）算法从时间序列之间的对齐路径长度开始，通过给定对齐路径长度上限LUB来限制时间序列之间的对齐路径长度。相比其他改进算法（如权重DTW［12-13］、窗口限制Sakoe-Chiba band［14］、Itakura parallelogram［15］、learned window［16］、改进进步模式step pattern［15，17］等）从局部限制每个数据点所能匹配对应数据点的数量，LDTW 算法在全局上限制对齐路径总体长度，保留局部对齐的灵活性，抑制“病态对齐”现象，在UCR 公共数据集上的分类效果有更明显提升。但LDTW 算法将原DTW算法中的二维累计代价矩阵扩张为三维矩阵，增大了时间复杂度，在多数数据集上进行分类实验的时间开销远大于原DTW 算法以及相关衍生算法。

本文对LDTW 算法进行改进，提出固定对齐路径长度的动态时间规整（FDTW）算法。通过分析LDTW 算法所需要计算的累计代价矩阵元素数量、时间序列长度和对齐路径长度上限之间的关系，调整LDTW 算法中控制对齐路径长度的策略，使得对齐路径长度由限制在某个范围内改为固定到某个数值上，从而降低累计代价矩阵元素的计算量，提高计算效率。

1 相关工作

1.1 DTW 算法

DTW 为了适应时间序列间的相位偏移和振幅变化，将时间序列数据点之间对齐方式由欧氏距离的“一对一”改为“一对多”。设X=｛x1，x2，…，xR｝和Y=｛y1，y2，…，yC｝是两条长度分别为R和C的时间序列。对齐路径π用于描述X和Y之间数据点的对齐关系，它被定义为包含K个二元组集合，每个二元组包含两个分别来自时间序列X和Y的数据点下标。π的表示如式（1）所示：

在以上条件约束下，X和Y之间所有对齐路径的集合记为AXY。DTW 目标是最小化两条时序数据中所有对应数据点的局部距离值之和，并以之作为全局距离值，其定义如式（2）所示：

其中：d(xi,yj)=|xi-yj|2。

DTW 算法采用动态规划思想利用递归公式将以上问题转换为对X和Y子序列问题的求解，如式（3）所示：

由于子序列问题相互交叠，直接采用递归方式会产生大量的重复计算，因此DTW 算法通过建立一个R×C累计代价矩阵M来存放子问题的解以避免重复计算。因此，需计算R×C个矩阵元素，DTW 算法的时间复杂度为O(R×C)。

DTW 算法为了使序列间的距离值最小，计算过程中可能出现“病态对齐”现象［18］。“病态对齐”示意图如图1 所示。时间序列A 与时间序列B 为不同类别，而与时间序列C 为同一类别，但DTW 算法通过大规模的“一对多”对齐，在序列A 和序列B 并不具有相似性的局部数据点之间进行匹配，最终使得AB之间距离值大于AC 之间的距离值，违背了同类序列之间度量值应更小的事实。图1（a）的弯曲路径长度为54，图1（b）的弯曲路径长度为51。“病态对齐”缺陷限制了DTW 算法的度量效果。

图1 病态对齐现象示意图Fig.1 Schematic diagram of pathological alignment phenomenon

1.2 LDTW 算法

DTW 算法在出现“病态对齐”现象的同时，对齐路径的长度K也会增大。因此，LDTW 算法通过对对齐路径总长度K进行限制来抑制“病态对齐”现象。

给定时间序列X和Y，令minS、maxS分别表示X和Y之间允许的最小对齐路径长度和最大对齐路径长度，即minS=max(R,C)，maxS=R+C-1。X和Y之间允许长度相同的对齐路径并不唯一，令AXYl为所有长度l的对齐路径集合；LUB为给定的对齐路径长度上限，则时间序列X和Y之间的LD距离值如式（4）所示：

LDTW 算法采用动态规划方法将问题转换为求解X和Y的子序列问题，并建立R×C×LUB的三维累计代价矩阵M，依次计算矩阵元素如式（5）所示：

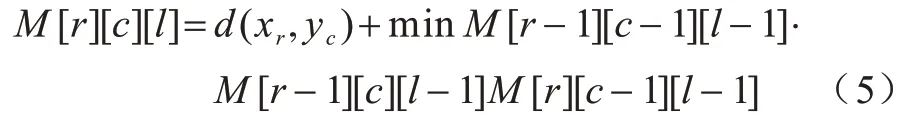
其中：M［r］［c］［l］值为子序列和子序列之间对齐路径长度l的最小距离值。由于不同长度的子序列之间可能产生的对齐路径长度范围不同，加上LUB限制，并非所有矩阵M的元素都需要计算，因此LDTW 算法按第三维优先顺序计算矩阵M，且在计算前先确定所有子序列间对齐路径长度的范围来避免不必要计算。

所有需要计算的矩阵元素计算完成后，元素M［R］［C］［minS］为minS长度的对齐路径对应的最小距离值；M［R］［C］［minS+1］为minS+1 长度的对齐路径对应的最小距离值；M［R］［C］［LUB］为LUB长度的对齐路径所对应的最小距离值。LDTW 算法从候选元素中选取最小值作为最终的度量值。该距离值所对应的对齐路径长度一定小于LUB，达到了从总体上控制长度以减少“病态对齐”现象的目的。

LDTW 算法引入对齐路径长度概念，将累计代价矩阵由原DTW 算法的二维扩展到三维，算法的时间复杂度也由原DTW 算法的O（R×C）增长为O（LUB×R×C），使得分 类过程的时间开销大于原DTW 及其衍生算法。

2 FDTW 算法

2.1 算法原理

在LDTW 算法中，当时间序列长度R为5，LUB为9 时计算的矩阵元素如图2 所示。从图2 可以看出，矩阵的第一、第二维度分别表示时间序列数据点下标，第三维度为对齐路径长度。根据式（5）可知，当前层元素值计算只与前一层中左方、上方和左上方的相邻元素值有关，与正下方的元素值无关，即矩阵元素M[r][c][l]的计算与M[r][c][l-1]无关。矩阵元素M[x5][y5][9]的计算无需元素M[x5][y5][8]参与，而M[x5][y5][8]的计算无需M[x5][y5][7]参与。若只计算长度等于LUB对齐路径对应的最佳距离值，相比计算出所有对齐路径长度小于LUB的最佳距离值所需要计算的累计代价矩阵元素数量更少，且仍保留通过限制长度以抑制“病态对齐”的原理。由于对齐路径长度被限定为阈值LUB，将这种方法称为固定对齐路径长度的DTW 算法。

图2 LDTW 算法的三维累计代价矩阵元素Fig.2 The three-dimensional cumulative cost matrix elements of LDTW algorithm

2.2 算法描述

FDTW 算法的目标是从所有长度为给定值的对齐路径中找出使得对应距离值最小的对齐路径，并将该最小值作为距离值。令X和Y表示待度量的两条时间序列，FL表示给定的对齐路径长度，则X和Y之间的FD距离值如式（6）所示：

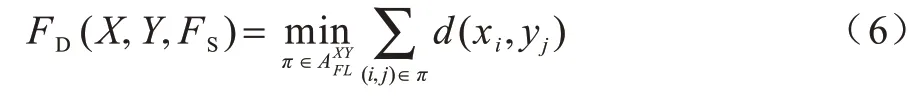
其中：表示序列X和Y之间所有长度为FL的对齐路径的集合。

利用递归公式将式（6）转化为对子序列间距离值的求解，如式（7）所示：

为避免对相同子问题进行重复求解，FDTW 算法建立三维累计代价矩阵M，采用动态规划方式从最小子序列开始依次对所有子序列间被允许的对齐路径长度下的距离值进行计算。使被计算的子序列在距离数量最小化的前提下求解出最终序列间距离，计算过程应当满足以下条件：1）计算某对子序列间的距离值时，其依赖的子序列距离值已经被计算；2）当前被计算的子序列间距离值一定会被后续的计算所依赖。

当序列长度为5 时，不同条件下计算的子问题如图3 所示。当时间序列X、Y长度为5 时，所有子序列问题如图3（a）所示（矩阵行列坐标和矩阵元素值分别对应两条子序列下标以及对齐路径长度）。为满足计算过程的条件1，将图3（a）中所有子序列问题全部求解，但在LDTW 算法中（LUB取为7），由于不需要求取序列X、Y之间对齐路径长度为8、9 对应的距离值。为满足计算过程条件2，将求解的其余子问题相应缩减为图3（b）的范围。在FDTW 算法中（FL为7），只需取序列X、Y之间对齐路径长度为7 对应的距离值，将求解的其余子问题进一步缩减为图3（c）的范围。范围缩减后某些子序列间不需要计算任何对齐路径长度下的距离值，其子序列在图3 中用阴影表示。

图3 不同条件下计算的子问题Fig.3 Sub-problems calculated under different conditions

为了使计算过程满足以上条件，FDTW 算法首先根据参数FL对所有子序列之间的对齐路径长度范围进行计算；其次在范围内计算各子序列距离值。因此，FDTW 算法步骤分为子序列间对齐路径长度范围计算和各子序列距离值计算。

2.2.1 子序列间对齐路径长度范围计算

长度分别为R和C的序列X和Y之间允许产生最小和最大对齐路径长度，其计算结果为：minS=max（R，C）、maxS=R+C−1。为方便描述，将minS和maxS组成的对齐路径长度范围［minS，maxS］称为原始对齐路径长度范围。子序列之间调整后的对齐路径长度范围如图4 所示，时间序列长度R=C=7，设FL为11，阴影元素[x6,y4]代表当前要计算子序列之间路径长度范围。从图4 可以看出，实线表示之间长度最大的一条对齐路径，其长度maxS=6+4-1=9；长虚线表示之间长度最小的一条对齐路径，长度minS=max（6，4）=6，因此子序列之间的原始长度范围为[6,9]。若子序列之间对齐路径长度为6，那么对齐路径总长度为FL，其互补子序列之间对齐路径长度为FL+1-6=6（加1 是对齐路径元素(π1(k),π2(k))被计算了两次）。子序列之间产生的对齐路径长度小于6；同样，若对齐路径在子序列之间长度为9，那么子序列之间对齐路径长度为FL+1-9=3，但子序列之间的对齐路径长度总是大于3。

图4 子序列和之间调整后的对齐路径长度范围Fig.4 Alignement path length range betweenand sub-sequence

因此，根据参数FL和互补子序列之间的原始对齐路径长度，对子序列间原始的齐路径长度范围的上限和下限进行进一步调整。

1）调整范围上限

算法1计算子序列间对最大对齐路径长度

算法2计算子序列间对最小齐路径长度

2.2.2 子序列之间距离值计算

确定子序列间对齐路径长度范围后，FDTW 算法根据式（5）计算每个矩阵元素，该过程和LDTW 算法相同，具体步骤可以用算法3 进行描述。算法3第3、第4 行建立累计代价矩阵并初始化；第6～14 行对累计代价矩阵进行计算，其中第8、第9 行调用算法1 和算法2 对子序列之间的对齐路径长度范围进行计算。

算法3FDTW 算法

2.3 算法时间复杂度

FDTW 算法的时间复杂度与累计代价矩阵中需要计算的累计代价矩阵元素数量相关，本文对LDTW 算法的累计代价矩阵元素数量N的分析过程中得出FDTW 算法的计算量。

LDTW 算法的N值与时间序列长度R、C以及对齐路径长度上限LUB相关（当时间序列长度不变时，N值随LUB变化）。为了找出N值与R、C和LUB之间的关系，LDTW 算法中累计代价矩阵拆分如图5 所示，用相同的边缘线条类型来体现拆分后各分量矩阵在原矩阵的坐标位置。将第一个包含坐标为［R，C］元素的分量矩阵及其之前的分量矩阵标记为a类分量矩阵，将其余分量矩阵标记为b类分量矩阵。从图5可以看出，根据先后顺序依次计算分量矩阵将满足以下规律：当前计算元素所依赖的元素都已在此之前计算完毕。从图5（a）可以看出，箭头在计算元素M［x4］［y4］［5］时，依赖的 三个元 素M［x3］［y3］［4］、M［x3］［y4］［4］和M［x4］［y3］［4］都已经完成计算。当所有a类分量矩阵计算完成时，长度等于LUB的对齐路径所对应的最小距离值则计算完成，该值是FDTW 算法在参数FL=LUB时的目标值。因此，a类分量矩阵元素数量是FDTW 算法的累计代价矩阵元素的计算量，而b类分量矩阵元素数量是FDTW 算法与LDTW 算法之间矩阵元素计算量的差值。

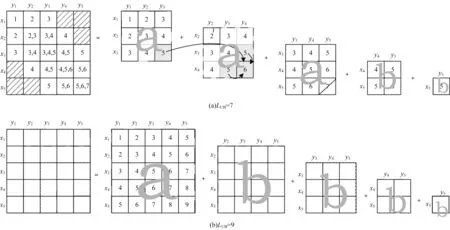
图5 LDTW 算法累计代价矩阵拆分Fig.5 Split the cumulative cost matrix of LDTW algorithm

根据确定序列间对齐路径长度范围的规则可知，a类分量矩阵个数为maxS−LUB+1，每个a类分量矩阵包含的元素数量为［R−（maxS−LUB）］［C−（maxS−LUB）］，则所有a类分量矩阵元素总数量如式（8）所示：

其中：m=maxS−LUB。

b类分量矩阵个数为LUB−minS，所有b类分量矩阵所包含的元素数量构成首项为|R−C|+1，二级首项为|R−C|+3，二级公差为2 的二阶等差数列，可推导出所有b类分量矩阵元素的总数量如式（9）所示：

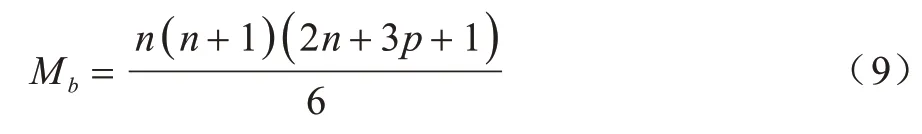
其中：n=LUB−minS；p=|R−C|。

当两条时间序列长度相等，即R=C时，所有a类分量矩阵元素总数量简化如式（10）所示：

其中：Ma为关于对齐路径长度上限LUB的三次函数，当LUB为（5R−4）/3 时Ma的取值范围如式（11）所示：

当两条时间序列长度相等，所有b类分量矩阵元素的总数量简化如式（12）所示：

N值为a类分量矩阵元素数量和b类矩阵元素数量之和，N=Ma+Mb。推算出N为关于对齐路径长度上限LUB的单调递增函数，N的取值范围如式（13）所示：

在以上推导过程中，N值代表LDTW 算法中需要计算累计代价矩阵元素的数量，Ma值代表FDTW 算法中需要计算的累计代价矩阵元素数量，Mb值为LDTW算法计算量和FDTW 算法之间的差值。由于对累计代价矩阵元素的计算是LDTW 算法和FDTW 算法的基本操作，累计代价矩阵元素数量即为算法基本操作的执行频度。从式（12）和式（13）可以看出，LDTW 算法和FDTW 算法累计代价矩阵元素数量都与时间序列长度呈三次方关系。因此这两种算法的时间复杂度都为O（n3）。当R=C=50 时，N、Ma、Mb随LUB变化对比如图6所示。从图6 可以看出，LUB取值越大，差值Mb越大。当两种算法的参数相同时，FDTW 算法计算量比LDTW算法更低。

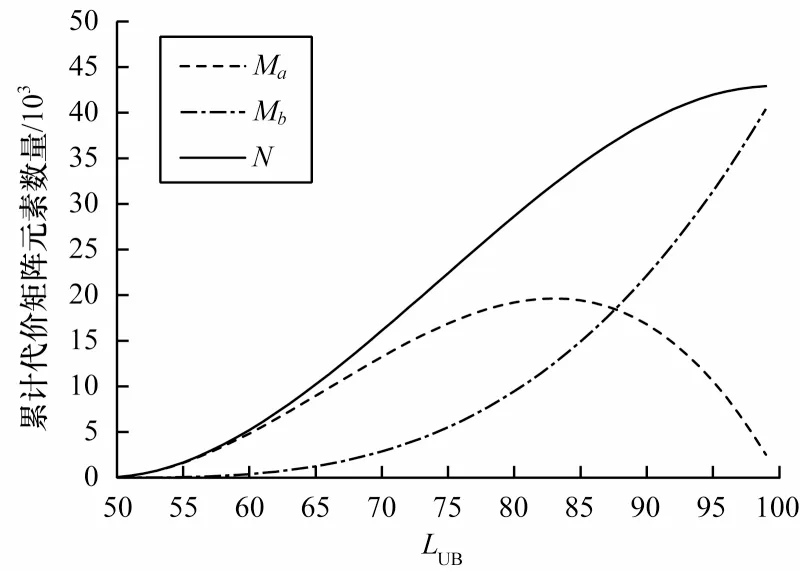
图6 N、Ma、Mb随LUB 变化对比Fig.6 Change comparison of N，Ma and Mb with respect to LUB

3 实验

为了与DTW 算法及其变体算法的相关工作保持一致，本文采用1-NN 分类方法，将FDTW 算法作为距离度量，在UCR 公共数据集上进行分类实验，以验证FDTW 算法的性能。

3.1 数据集

近年来，UCR 时间序列数据文档［19］被研究者广泛引用，本文从该数据文档中选取序列长度分布在60～637 的37 个数据集进行实验。所选取的数据集如表1 所示。

表1 数据集参数信息Table 1 Parameters information of data set

3.2 FDTW-1NN 分类结果

最近邻分类方法因无需设置参数，分类结果仅依赖于度量方式而被广泛采用，本文采用该方法进行分类实验。ED 距离、DTW 算法、Sakoe-Chiba 窗口DTW算法、LDTW 算法以及FDTW 算法在相同数据集上的分类准确率如表2 所示。其中，w 是Sakoe-Chiba 窗口DTW 算法的参数，即窗口宽度占序列长度的百分比。Sakoe-Chiba 窗口DTW 算法、LDTW算法以及FDTW算法设置的参数值标注在准确率右侧，该参数都由交叉验证法在训练集上学习得到。从表2 可以看出，LDTW 算法和FDTW 算法在绝大多数数据集上取得最佳分类准确率。与LDTW 算法相比，在WordSynonyms数据集上，FDTW 算法的分类准确率最多提高了7 个百分点，在Lightning7 数据集上，最多降低了4 个百分点。

表2 不同算法的分类准确率对比Table 2 Classification accuracy comparison between different algorithms

FDTW 算法与其他算法的分类准确率对比如图7所示。从图7 可以看出，黑点代表各数据集，对角线代表中线，若黑点位于该线上则代表两种算法准确率相等。从图7（a）、图7（b）、图7（c）可以看出，相比ED 距离、DTW 算法、Sakoe-Chiba 窗口DTW 算法，FDTW 算法在绝大多数数据集上表现更优（相比ED距离有29个，相比DTW 算法有28 个，相比Sakoe-Chiba窗口DTW 算法有27个），在部分数据集上持平（相比ED距离有5个，相比DTW 算法有4 个，相比Sakoe-Chiba 窗口DTW 算法有5 个），部分数据集上呈略微劣势（相比ED 距离有3个，相比DTW算法有5个，相比Sakoe-Chiba窗口DTW算法有5 个）。从图7（d）可以看出，相比LDTW 算法，FDTW 算法的分类正确率在22个数据集上持平，在8个数据集上胜出，7 个数据集上呈劣势。

图7 FDTW 算法与其他4 种算法的分类准确率对比Fig.7 Classification accuracy comparison between FDTW algorithm and the other four algorithms

与高准确率相比，算法提前在哪些数据集上能取得高的准确率更能体现算法的可靠性［20］。本文采用文献［20］提出的增益混淆矩阵对FDTW 算法的可靠性进行评估。通过式（14）分别计算FDTW 算法与对比算法（competitor algorithm）之间的预期准确率增益和实际准确率增益：

计算预期增益时，将交叉验证过程中在训练集上取得的最高准确率作为预期准确率，而计算实际增益时，在测试集上进行分类实验的结果作为实际准确率。FDTW 算法与其他4 种算法间预期准确率增益和实际准确率增益对比如图8 所示。其中每个点代表一个数据集，每个点会出现在4 个区域中的一个区域（包括边缘），这4 个区域分别是：1）真阳性（TP），数据点出现在此区域是预计在该数据集上提高准确率，而实际上确实提高了，出现在该区域的数据点越多，证明算法可靠性越强；2）真阴性（TN），数据点出现在此区域是预计在该数据集上准确率降低，而实际上确实降低了，如果出现在该区域的数据点过多，应避免在此数据集上使用被提出的算法；3）假阴性（FN），数据点出现在此区域中是预计在该数据集上准确率降低，实际上准确率有所提高；4）假阳性（FP），数据点出现在此区域中是预计在该数据集上准确率会提高，但实际上准确率却下降了，出现在该区域的数据点越多，说明算法的可靠性越差。

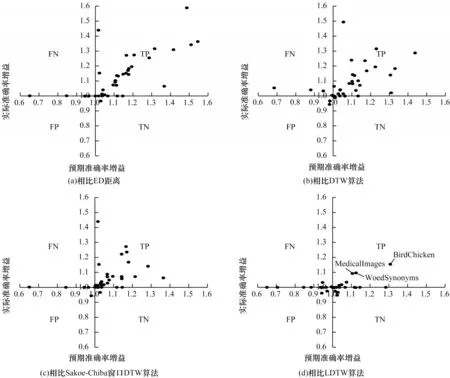
图8 FDTW 算法与其他4 种算法的预期准确率增益和实际准确率增益对比Fig.8 Expected accuracy gain and actual accuracy gain comparison between FDTW algorithm and the other four algorithms

从图8（a）～图8（c）可以看出，绝大多数数据点都落入TP 区域，说明相比ED 距离、DTW、Sakoe-Chiba 窗口DTW3 种算法，FDTW 算法的分类准确率得到提高是可靠的。从图8（d）可以看出，虽然落入TP 区域的数据点有所减少，但减少的这些数据点并没有落入其他区域，而是处于横轴边缘，说明在测试集上的分类准确率没有降低。相比其他区域，落在TP 区域的数据点更明显，因为在部分数据集上有较高的预期准确率增益和实际准确率增益（如BirdChicken 和WordsSynonyms 数据集），说明FDTW 算法与LDTW 算法相比，在分类准确率上有着持平的结果是可靠的。

3.3 时间开销对比

由2.3 节可知FDTW 和LDTW 算法的时间复杂度都为O(n3)，但在参数相同时，FDTW 算法需要计算的累计代价矩阵元素数量比LDTW 算法更少。为进一步对比FDTW 和LDTW 算法的计算量，选取两种算法所需参数相同的8 个数据集，分别记录两种算法在分类过程中所花费的时间以及两者之间的差值。两种算法在这8 个数据集上的分类准确率是持平的。参数相同的数据集下FDTW 和LDTW 算法的时间开销如表3 所示。为了体现两组时间数据差异，FDTW 和LDTW 算法分类时间开销对比如图9所示。从图9 可以看出，FDTW 算法在所有数据集上的分类时间开销都小于LDTW 算法，时间开销最多减少了10%（Ham 数据集）。

图9 FDTW 和LDTW 算法分类时间开销对比Fig.9 Classification time cost comparison between FDTW and LDTW algorithms

表3 在参数相同的数据集下FDTW算法和LDTW算法的时间开销对此Table 3 Time cost comparison between FDTW and LDTW algorithms on the data sets with same parameter

为了更直观体现FDTW 算法和LDTW 算法计算量的差异，选取了长度最短的数据集SyntheticControl，将两种算法在该数据集上的三维累计代价矩阵元素对比如图10 所示。在参数相同的情况下，与LDTW 算法相比，FDTW 算法的累计代价矩阵减少了部分右上角的元素，从而相应减少了时间开销。

图10 在SyntheticControl数据集上LDTW 与FDTW 算法计算量对比Fig.10 Calculation amount comparison between LDTW and FDTW algorithms on the SyntheticControl data set

3.4 参数对齐路径长度（FL）的选取

参数FL是FDTW 算法所需的唯一参数，该参数的选取将影响数据集的分类准确率。为了选取更合适的FL参数，本文采用10 折交叉验证法从各数据集包含的训练集上对该参数进行学习。将训练集划分为10 份，每次将其中一份作为训练集，其余作为测试集，依次计算出参数FL在所有可能取值下的准确率（即FL的步长为1）。该过程在不同测试集上重复10 次，取均值作为该FL参数下的最终准确率，然后选取最高准确率所对应的FL参数值作为最终的参数值。计算两条时间序列在不同FL值下的FDTW 距离值，会出现累计代价矩阵元素被重复计算的现象，例如，对于任何两条时间序列，FL无论如何取值，累计代价矩阵的第一个元素M［1］［1］［1］都将被计算，说明在交叉验证过程中，FL有多种取值可能，元素M［1］［1］［1］就会被计算多次。本文在进行交叉验证过程中，采用LDTW 算法，将参数LUB设定为maxS，从而在一次累计代价矩阵的计算过程中得出两条时间序列之间所有对齐路径长度下的弯曲距离值，以此来避免重复计算数据集。

在不同数据集上交叉验证性FL值对比如图11所示，从图11 可以看出，部分数据集的最佳准确率所对应的FL值并不唯一，本文选取更小的FL值，因这些FL值通常小于（5R−4）/3，根据2.3 节当FL小于（5R−4）/3 时，FL值越小，算法的计算量越小。

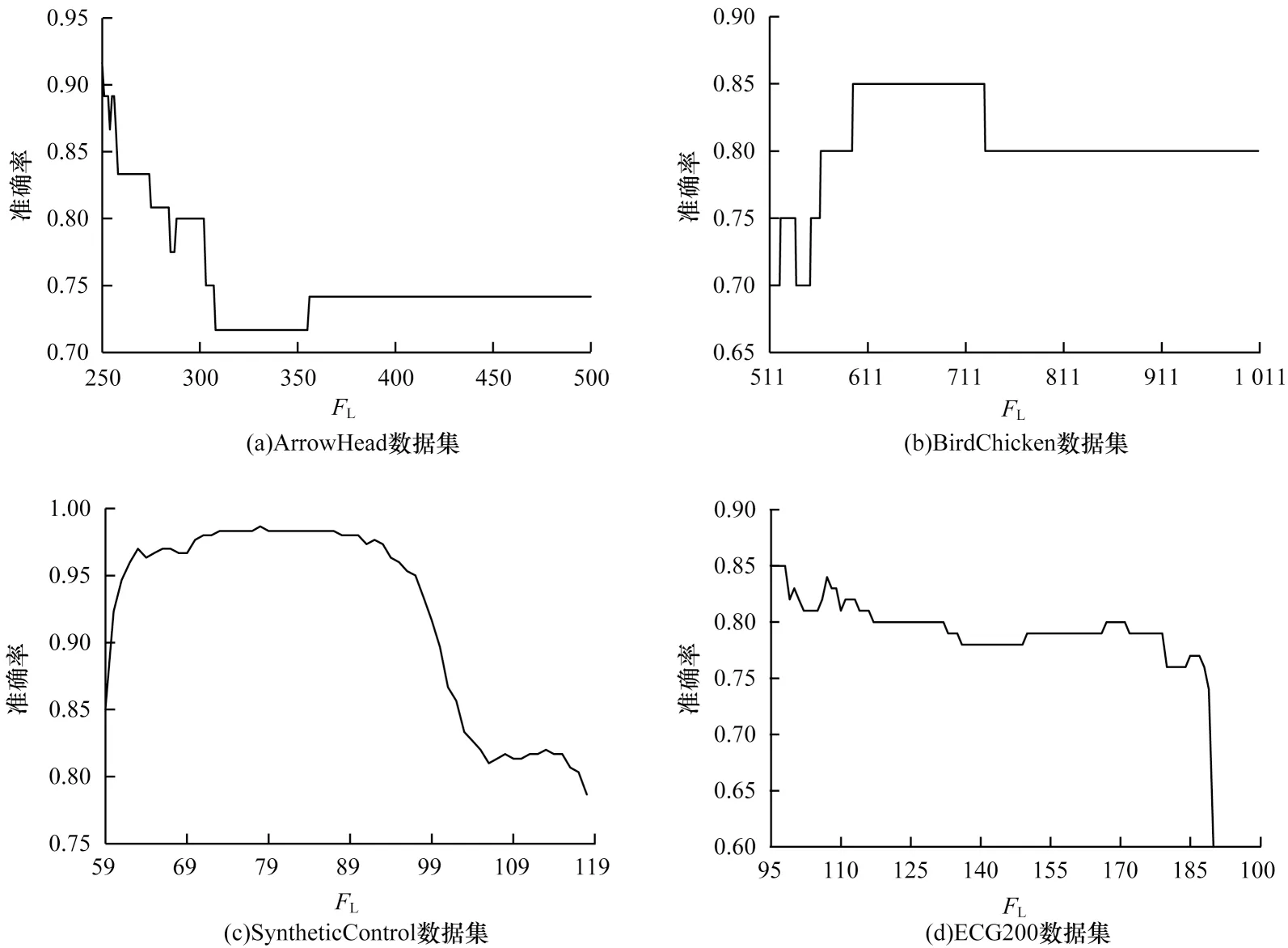
图11 交叉验证产生的FL对比Fig.11 Comparison of FL generated by cross-validation

从数据集ArrowHead 和ECG200 中可以看出，它们最佳分类准确率对应FL值靠近或等于minS，说明对齐路径长度与时间序列长度相等，此时的FD距离值与ED 值等价。同时从表1 可以看出，这些数据集在ED 距离下的分类准确率和FD距离及FD距离对应的准确率相似。因为这类时间序列存在较小的时滞（相位偏移），在ArrowHead 和BirdChicken 数据集上时滞对比如图12 所示。从图12（a）可以看出，数据集ArrowHead 中的序列只在垂直方向上存在一定噪声（振幅差），横向上几乎不存在相位偏移，在这样的时间序列之间，欧氏距离更适合作为度量方式。从图12（b）可以看出，BirdChicken 数据集中序列之间相位偏移和振幅差同时存在，此时欧氏距离不再有较好的度量效果。经过交叉验证后选取的参数FL，能够反应序列之间在横向上相位偏移的大小，即时滞的严重程度，使得后续分类更为准确。

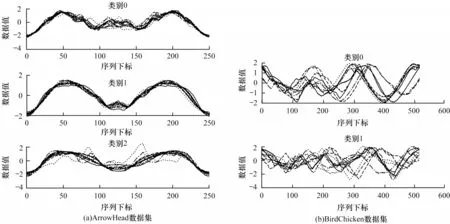
图12 在ArrowHead 和BirdChicken 数据集上的时滞对比Fig.12 Time lag comparison between ArrowHead and BirdChicken data sets

4 结束语

针对LDTW 算法计算量较大的问题，本文提出FDTW 算法。通过调整LDTW 算法中对齐路径长度的控制策略，以减少累计代价矩阵中需要计算的元素数量。在UCR 时间序列数据集的实验结果表明，与其他时间序列距离度量（ED 欧氏距离、DTW动态弯曲距离和DTWSC窗口动态弯曲距离）相比，FDTW 算法在大多数数据集上具有更高的准确率，其与FDTW 算法的分类准确率呈持平状态，且时间开销更小。后续将研究如何在保留限制对齐路径长度的同时降低时间复杂度，进一步提高FDTW 算法的计算效率。