一种基于轻量级神经网络的高铁轮对轴承故障诊断方法

2021-11-17邓飞跃吕浩洋郝如江刘永强

工程科学学报 2021年11期

邓飞跃，丁浩，吕浩洋，郝如江，刘永强

1) 石家庄铁道大学省部共建交通工程结构力学行为与系统安全国家重点实验室, 石家庄 050043 2) 石家庄铁道大学机械工程学院, 石家庄, 050043

近年来，中国高速铁路飞速发展，运营里程位居世界第一. 与此同时，高速列车运行带来的安全问题愈发引人关注. 轮对轴承作为高速列车走行部关键旋转部件之一，工作环境非常恶劣，极易发生各类故障，但是其故障诊断较为困难，运行维护一直处于一种定期拆解、强制报废的过度维修状态[1−3]，造成了资源的大量浪费. 因此，准确诊断与检测轮对轴承故障是一个亟待解决的突出问题.

目前，“特征提取+机器学习”的智能诊断方法在轴承故障诊断中得到了广泛应用. Dong等[4]通过局部均值分解方法分解轴承故障信号，计算每个分量的香农熵输入K−最近邻（K-nearest neighbor,KNN）模型识别轴承不同故障损伤程度；Shao等[5]使用变分模态分解方法处理信号，提取多尺度故障特征信息后输入支持向量机（Support vector machine, SVM）对轴承复杂故障类型进行智能识别. 上述方法多使用浅层机器学习模型，面对大量且复杂的监测数据时无法准确表征特征信息与健康状态之间的映射关系.

随着人工智能技术不断进步，基于深度学习的轴承故障诊断方法蓬勃发展. 该类方法基于数据驱动模型，将特征学习与智能识别同时嵌入网络模型内部，在深入挖掘特征信息的基础上，能较为准确地识别轴承健康状态，不需要复杂的信号处理技术[6−9]. Zou等[10]采用离散小波变换处理信号，建立了改进的深度信念网络模型(Deep belief network，DBN)，对高速列车牵引电机轴承故障进行了诊断和识别. Shao等[11]提出了一种基于双树复小波包的自适应DBN模型用于轴承故障诊断.Wang等[12]提出了一种新的激活函数ReLTanh，并通过构建自编码(Auto-encoder，AE)网络模型来诊断齿轮箱各类故障. 相比上述网络模型，卷积神经网络（Convolutional neural network, CNN）采用了局部感受野和权值共享策略，网络结构及训练优化更为简单、效率更高[13−15]. Chen等[16]构建了一个深度CNN模型，通过输入传感器多通道信号实现了旋转机械不同故障模式的识别；Zhang等[17]则提出了另一个CNN模型用于轴承故障诊断，针对强噪声干扰和变工况负载具有较高的识别准确率；Peng等[18]采用残差神经网络用于列车轮对轴承故障诊断，达到了很高的诊断精度. 由于历时长、测点多，采样频率高等原因，轮对轴承监测系统获取的是海量数据[19]. 传统深度神经网络（Deep neural network, DNN）分析时模型复杂度会大幅增加，不仅对计算机硬件配置提出了更高要求，而且运行效率也大打折扣，这严重限制了其在实际工程中的应用.

为解决上述问题，本文提出了一种新的轻量化神经网络ShuffleNet模型，用于轮对轴承故障诊断研究. 该模型基于模块化设计思想，在卷积网络基础上设计了多个高效的ShuffleNet单元，通过综合运用分组卷积（Group convolution, GC）、深度可分离卷积 (Depthwise separable onvolution, DSC)与通道混洗（Channel shuffle, CS）技术，在保证网络诊断精度准确率的同时，极大地提升了模型的运算效率，减少了网络运行对计算力的需求. 实验结果表明，该模型可有效用于高速列车轮对轴承故障诊断，具有较好的工程应用价值.

1 背景理论

1.1 标准卷积

CNN提取特征信息主要是通过卷积层操作完成的. 卷积层通过卷积核对上一层网络输出特征进行反复的局部卷积操作，将学习到的特征信息提取到下一层，其过程表示为：

其中，x为卷积层输入，y是卷积层输出，U为当前层的权重矩阵，∗为卷积操作，b为卷积核的偏置.f()为激活函数，用于增强学习特征的非线性表达能力.

标准卷积过程中，每个通道的输入特征信息通过卷积核都可以输出到每个输出特征. 设定输入特征通道数为W，卷积核通道数与输入特征通道数相同，卷积核个数为B，与对应输出特征通道数相同. 卷积核尺寸大小为D×D，对应参数为D×D×W×B，. 经过计算，此次卷积过程的参数量如下：

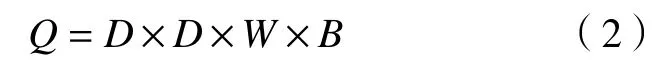
1.2 分组卷积

GC将输入特征进行了分组，然后再进行卷积操作，过程如图1所示. 基于上述相同输入与输出特征的设定，若输入特征分为G组，则每组输入特征数量为W/G，相应卷积核分组后，每组中卷积核只与同组的输入特征进行卷积操作，卷积核数量与输出特征数量相同，均为B/G. 计算参数量为：

图1 分组卷积Fig.1 Group convolution

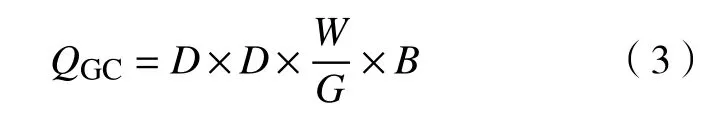
GC后参数量变为原来标准卷积的 1 /G，随着分组数增加，参数量会明显减少. 此外，Krizhevsky等[20]指出GC除能够减少训练参数外，不易产生过拟合，具有正则化的效果.

1.3 深度可分离卷积

标准卷积操作过程中，卷积层中每个卷积核分别与每个通道的输入特征进行卷积操作，卷积结果线性叠加后即为相应的输出特征. 标准卷积操作如图2所示，其中输入特征尺寸大小N×N，通道数为3；输出特征通道数为2，尺寸大小为M×M；卷积核参数为D×D×3×2，尺寸大小为D×D. 从图中可知，标准卷积过程中同时考虑了输入特征的通道数与卷积区域. 卷积过程中参数量大小为：

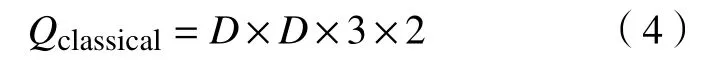
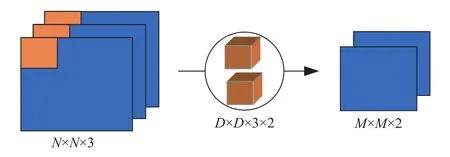
图2 标准卷积操作Fig.2 Classical convolution operation

与标准卷积操作不同，DSC卷积操作分为深度卷积（Depthwiseconvolution，DWConv）和逐点卷积（Pointwise convolution, PWConv）两个步骤. 在DWConv中，卷积核数量与输入特征通道数相同，一个卷积核只与一个通道的输入特征进行卷积操作，因此输出特征通道数与输入特征通道数相同.需要指出的是，当GC中分组数与输入特征通道数、卷积核个数相同时，GC就是DWConv. PWConv与标准卷积操作相同，但卷积核采用尺寸大小为1×1的单位卷积. 相同参数条件下，上述两个步骤的操作分别如图3（a）和 3（b）所示，从图中可知DSC先考虑卷积区域，再考虑输入特征通道，实现了通道与卷积区域的分离. DSC操作过程中参数量大小为：

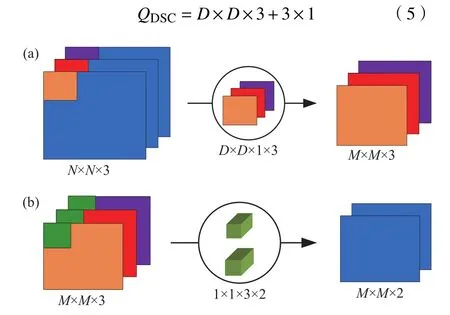
图3 深度可分离卷积操作. （a）DWCnov 操作；（b）PWConv 操作Fig.3 Depthwise separable convolutionoperation: (a) DWCnov operation; (b) PWConv operation

通过对比式（4）和式（5）可知，DSC 的参数量要小于标准卷积，尤其当卷积核的数量及输入输出通道数大幅增加时，参数量的减少将相当可观.此外，Howard等[21]通过研究进一步证实：DSC所需要的计算量也远小于标准卷积. 因此，相比标准卷积，使用DSC的计算力将大为节省.

1.4 通道混洗

GC虽然具备诸多优点，但是分组后由于每组卷积核只与同组输入特征进行卷积操作，如图4（a）所示. 在分组约束下，各组之间是相互孤立的，没有信息的交互流通，输出特征仅从一小部分输入通道组中导出，降低了卷积过程中信息的表示能力. 为此，我们通过CS技术对输入层特征进行混洗操作，将不同组输入特征重新分组，打破各组之间的约束，过程如图4（b）所示. 假设输出层特征图分为G组，每组包含w个通道输入特征，CS具体实现步骤如下：

图4 （a）通道孤立与（b）通道混洗的区别Fig.4 Differencebetween (a) channel isolation and (b) channel shuffle

步骤一：将具有G×w通道的输出特征reshape为（G,w）格式；

步骤二：将（G,w）格式的输出特征转置为（w,G）格式；

步骤三：对（w,G）格式的输出特征进行平坦化处理，再次分为G组，作为下一层输入特征.

为了能更清楚地描述CS过程，假设G=w=3，CS操作过程如图5所示. 从图中可知，输出特征层虽然分为了3组，但GS后组与组之间的约束被打破，不同组之间的特征通道是关联的，每组内包含了不同通道的特征信息. 在本文分析过程中，为保证通道混洗的效果，设置G与w数值相同.

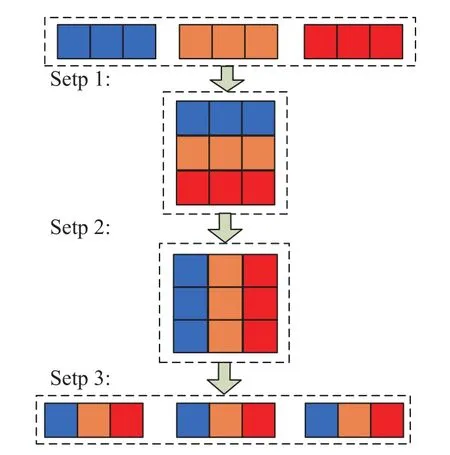
图5 通道混洗操作Fig.5 Channel shuffle operation

2 ShuffleNet模型

2.1 ShuffleNet单元

残差网络（ResNets）由He等[22]在2015年首次提出. ResNets在残差块中通过引入跨层恒等映射连接，有效解决了网络层数增加时的梯度消失问题. 基于残差块结构，Zhang 等[23]构建了如图6（a）所示的ShuffleNet单元. 从图中可知，ShuffleNet单元采用了跨层恒等映射连接的两分支结构，主分支上首先是逐点GC，然后进行CS，之后是卷积核大小为3×3的DWConv和逐点GC操作，两分支输出特征线性叠加后即为最后输出特征. 这里需要指出的是主分支最后的逐点GC可以看做是一个分组的PWConv过程，因此3×3DWConv和1×1GC操作结合其实是一个DSC操作. 图6（b）是一个降采样后的ShuffleNet单元，与图6（a）相比主要有两点不同：一是在辅分支上加入了步长为2、尺寸大小为 3×3 的平均池化（AVG pool），相应主分支上的3×3DWConv步长也由1改为2；二是ShuffleNet单元最终输出为两个分支的通道级联而线性叠加. 通道级联设计使得ShuffleNet单元最终输出特征通道数为输入特征的2倍，通过扩大输出特征的宽度，进一步增强网络模型的特征学习能力. 需要说明的是，ShuffleNet单元中每一个卷积层后都加入了批量归一化操作（Batch normalization, BN）来防止梯度消失、加快训练速度，在部分层后还加入了使用激活函数ReLU的激活层.

图6 ShuffleNet单元结构. （a）ShuffleNet单元 1; （b）ShuffleNet单元 2Fig.6 Architecture of ShuffleNetunit: (a) ShuffleNet unit 1; (b) ShuffleNet unit 2

2.2 ShuffleNet网络模型

基于模块化设计思想，本文以ShuffleNet单元为基本模块，构建轻量级ShuffleNet网络模型，如图7所示. 由于所分析数据格式是一维的，无法与所提二维网络模型兼容，本文参考文献[24]中的方法，将一维数据转化为二维图像格式后再输入网络. 网络首层采用了一个尺寸大小为3×3的标准卷积操作，然后是4个ShuffleNet单元. ShuffleNet单元数量过少会无法充分提取数据特征信息，而数量过多又会导致网络结构复杂，运行效率下降.本文通过分析对比，选择4个ShuffleNet单元构建模型，后面会通过t−分布式随机邻域嵌入（t−SNE）操作对模型中特征信息的聚类效果进行可视化处理，来进一步验证其合理性. 之后，对每个通道的输出特征进行全局平均池化（Global average pooling，GAP），添加Dropout层减缓过拟合的影响. 最后，使用全连接层并进行Softmax分类输出，对轮对轴承不同健康状态进行智能识别. 网络模型的具体参数设置如表1所示.

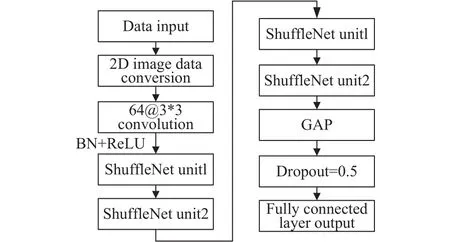
图7 ShuffleNet网络模型结构Fig.7 Architecture of ShuffleNet model

表1 网络参数设置Table 1 Parameter settings of network

3 实验分析与讨论

3.1 实验介绍

实验是在高速列车轴承综合实验台上完成的，实验台结构如图8所示，实验台一端为连接电机的支撑轴承，另一端为测试用轮对轴承. 实验台通过液压加载装置可以对轮对轴承施加径向和轴向静态加载，还可以模拟轨道谱激励进行动态加载. 因此通过该实验台能够模拟高速列车实际运行过程中轮对轴承较为真实的载荷工况，满足不同速度等级和负载工况下的高速列车轮对轴承跑合实验. 实验对象为CRH380B型高速动车组中采用的FAG系列双列圆锥滚子轮对轴承，通过线切割方式在轴承内圈和外圈表面加工出长为5mm、宽为1mm、深为0.7mm的微小凹痕故障，如图9所示. 加速度传感器安装在轴承端盖处，采样频率为 51200 Hz.

图8 高速列车轴承综合实验台Fig.8 Wheelset bearing comprehensive test rig of high-speed train

图9 故障轮对轴承. （a）内圈故障；（b）外圈故障Fig.9 Wheelset bearing: (a) inner race fault; (b) outer race fault

实验中共进行了4种不同速度等级的高速列车轮对轴承跑合试验，获得的具体实验数据如表2所示，每种测试包含无载荷、静载和动载3种载荷工况，每种工况下分别进行了轮对轴承内圈故障、外圈故障及正常状态3种不同健康状态的测试. 针对每一类健康状态，我们分别采集了1000组信号样本，每组样本包含1024个数据点，共计1000×36=36000组信号样本. 每类健康状态中，随机选取200组样本作为测试样本，其余作为训练样本. 采用五折交叉验证方法对网络进行训练，确定最优网络模型后，输入测试集进行测试分析，测试过程重复5次，最终结果取均值.

表2 实验数据Table 2 Experimental data

3.2 实验结果

样本信号输入网络模型前，统一进行了归一化处理. 实验过程采用了Adam优化算法更新网络参数. 网络训练过程中，初始学习率为0.001，每10个迭代步学习率减小到原来的1/10，共进行40个迭代步训练，批量大小为64. 网络模型训练和测试的分类准确度如图10所示. 从图中可知，网络训练和测试过程中，分类准确率均接近100%，损失值接近0，两者在20个迭代步后都能够达到有效收敛并保持稳定. 结果显示，我们通过本文方法可以准确地识别轮对轴承在不同速度等级及不同载荷状态下的健康状态.

图10 所提网络的分类准确度Fig.10 Classification accuracy of the proposed network

3.3 分析讨论

首先分析不同分组数对本文所提方法的影响，设置分组数G分别为2、4和8，分析数据为实验室原始数据，模型分析结果如表3所示. 表中，浮点运算次数（Floating point operations, Flops）指标用于衡量网络模型的复杂度. 从表中可知，3种不同分组数情况下，测试精度都接近100%. 随着分组数增加，网络模型的参数量和Flops都明显减少，这与公式（3）相对应. 但是，模型运算时间却是G=2时最少，究其原因，Zhang等[23]指出分组数的增加虽然会减少模型的计算量和参数量，但随之带来的密集操作会使计算机的计算及存储访问效率更差，实际运行时间更长. 因此，实际应用中，分组数并不是越大越好，在后面分析中设置网络模型的分组数为G=2.

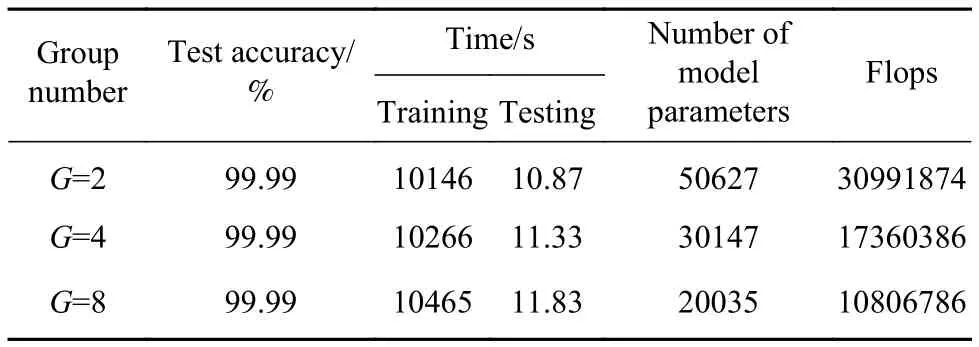
表3 不同分组数的对比结果Table 3 Comparison result of different groups

为了更符合实际工况，我们在原信号基础上添加了不同信噪比（Signal noise ratio, SNR）的高斯白噪声，SNR 分别为−20 dB、−15 dB 和−10 dB. 通过对含噪信号进行分析，来进一步验证所提方法的有效性. 我们选取传统CNN、ResNets和Xception[25]3种网络模型与本文所提出的网络模型进行对比.其中，传统CNN中卷积层数与本文模型中卷积层数量相同，ResNets中残差块数量与本文模型中ShuffleNet单元数量相同. 针对不同信噪比的含噪信号及原信号，4种方法的诊断结果如图11所示.从图中可知，随着噪声的减少，所有方法的诊断精度均有所提升. 总体来看，本文方法在分析不同信噪比信号及原信号时，诊断精度要优于传统CNN方法，与ResNets和Xception结果基本相同，均能保证较高的诊断准确度.

图11 不同方法的分类准确度Fig.11 Classificationaccuracy of different methods

我们以SNR=−20 dB的含噪信号为分析对象，进一步分析了上述4种方法的运行效率，结果如表4所示. 从表中可知，本文所提模型的训练时间和测试时间要明显少于传统CNN、ResNets与Xception方法，模型参数量和Floaps也远小于其他3种对比方法. 需要指出的是，随着网络模型深度及所分析数据量的进一步增加，所提方法的运行效率优势会更为明显. 由于添加噪声信号相比原始信号更为复杂，网络模型分析含噪信号的运算时间要稍显增加.

表4 不同方法的运行效率对比Table 4 Comparison of operation efficiency of different methods

T−SNE作为一种用于挖掘高维数据的非线性降维算法，能够很好地将高维数据映射到二维空间. 基于此，我们通过T−SNE对本文所提网络不同阶段的特征聚类结果进行了可视化分析，进而观察网络内部的特征学习过程. 图12显示了网络模型包含4个ShuffleNet单元时不同阶段的特征分布情况. 通过观察可知，在网络输入端，不同健康状态的轮对轴承特征信息混在一起；标准卷积层后，特征信息开始出现聚类趋势；随着网络深度增加，聚类效果逐渐清晰；第4个ShuffleNet单元处理后，不同类型的特征信息已经完全分离.为了进一步对比分析，选取3个ShuffleNet单元构建的网络模型，并对原始信号进行分析处理，模型不同阶段的可视化结果如图13所示. 从图中可知，第3个ShuffleNet单元处理后，不同类型的特征信息仍有零星混叠，不能彼此完全分离，这说明本文选用4个ShuffleNet单元构建网络是较为合理的，可以准确识别轮对轴承不同类型的健康状态.

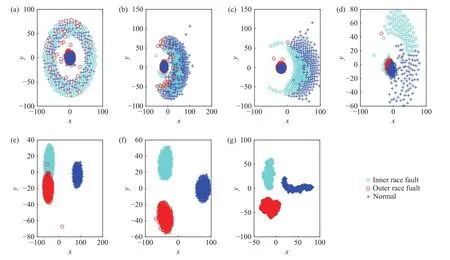
图12 4 个 ShuffleNet单元网络模型不同阶段的可视化结果. （a）网络输入端；（b）卷积后；（c）首个 ShuffleNet单元后；（d）第二个 ShuffleNet单元后；（e）第三个 ShuffleNet单元后；（f）第四个 ShuffleNet单元后；（g）GAP 后Fig.12 Visualization results of the proposed network with 4 ShuffleNet units at different stages: (a) model input; (b) after convolution operation; (c) after the first ShuffleNet unit; (d) after the second ShuffleNet unit; (e) after the third ShuffleNet unit; (f)after the fourth ShuffleNet unit; (g) after the GAP

图13 3 个 ShuffleNet单元网络模型的不同阶段可视化结果. （a）网络输入端；（b）卷积后；（c）首个 ShuffleNet单元后；（d）第二个 ShuffleNet单元后；（e）第三个 ShuffleNet单元后；（f）GAP 后Fig.13 Visualization results of the proposed network with 3 ShuffleNet units at different stages: (a) model input; (b) after convolution operation; (c) after the first ShuffleNet unit; (d) after the second ShuffleNet unit; (e) after the third ShuffleNet unit; (f) after the GAP