钢丝绳扭转系数研究

郭相参

(中国恩菲工程技术有限公司， 北京 100038)

1 前言

在“双超”课题中对钢丝绳罐道提升容器安全间隙进行了研究，得出引起提升容器水平摆动位移的3个主要因素：①提升钢丝绳扭矩的作用；②科里奥利力；③气动侧向压力。提升容器的最大水平摆动位移可通过Umax=Fmax/Kmin计算，Fmax为水平作用力最大值，其大小主要受上述三个因素影响，Kmin为钢丝绳罐道刚性系数最小值。而影响Fmax大小的主要因素之一的提升钢丝绳扭矩通常用M=CQDF计算，CQ为钢丝绳扭转系数，D为钢丝绳直径，F为钢丝绳承受的载荷。钢丝绳结构的复杂性使得其扭转系数很难准确确定，故难以准确计算提升钢丝绳受拉时产生的扭矩，进而也就无法确定钢丝绳罐道提升容器的最大水平摆动位移对其安全间隙的影响程度。

本文针对不同结构的钢丝绳扭矩模型，推导出扭矩计算公式，并通过特定结构钢丝绳的扭矩计算拟合出扭转系数的通用公式，然后又从钢丝绳结构和捻角方面分析了其对钢丝绳扭转系数的影响，最后对钢丝绳的生产和选用提出了思考，供相关从业者参考。

2 钢丝绳扭矩

钢丝绳由多根钢丝捻成股绳,数根股绳再捻制而成。对于提升钢丝绳而言，其上下两端均不能自由旋转，故而产生扭矩。钢丝绳扭矩由股绳绕轴线、股中丝对绳轴线的扭矩组成。而在计算钢丝绳扭矩时需对其计算模型进行理想化假设：①钢丝绳用等直径钢丝捻制；②钢丝绳受拉时其各层股绳、股绳中的各层丝受力均匀。钢丝绳的结构不同，其受拉时产生的扭矩模型也就不同。

2.1 单股钢丝绳

单股钢丝绳受拉时受力分析如图1所示，分解到垂直于钢丝绳轴线的力F″=Ftanα/n，则钢丝绳的扭矩为

图1 单股钢丝绳受力分析

(1)

式中：M——钢丝绳扭矩，kN·m；

F——钢丝绳承受的荷载，kN；

n——钢丝绳钢丝根数；

ni——第i层丝钢丝数；

ri——第i层丝钢丝捻制半径，m；

αi——第i层丝的捻角；

k——钢丝绳钢丝层数。

若k=1时，式(1)简化为

(2)

对于一层丝单股钢丝绳而言，n=n1，则M=Frtanα。

2.2 交互捻钢丝绳

交互捻钢丝绳的扭矩由股绳绕轴线、股中丝对绳中心线的扭矩组成。以右交互捻钢丝绳为例，由式(1)可知，多层股股绳对绳中心线的扭矩大小为

(3)

式中：n——钢丝绳股绳总数；

nj——第j层股绳数；

rj——第j层股绳捻制半径，m；

αj——第j层股绳的捻角；

m——钢丝绳股绳层数。

若m=1时，当钢丝绳由一层股绳组成时，股绳对绳中心线扭矩按计算。

股绳中钢丝受拉时的受力及其对绳中心线的扭矩分析如图2、图3所示，分解到平行股绳中心线的力F′=F/(ncosα)，F′垂直于股中心线的分力为F″s，则

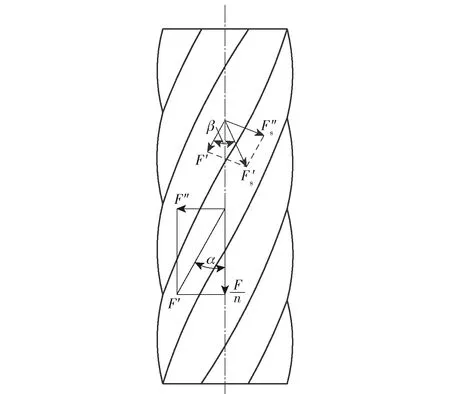
图2 交互捻受力分析图

图3 交互捻力和扭矩分解图

(4)

F″s产生的扭矩为

(5)

式中：ns——股绳钢丝总根数；

nsi——股绳第i层钢丝数；

β——股绳第i层钢丝对股中心线的夹角；

rsi——股绳第i层钢丝捻制半径，m。

矢量M′s与矢量M有着一个夹角θ，如图3所示。根据力的方向，有∠θ=∠γ=∠α。所以M′s在垂直于钢丝绳轴线的分量Ms为

(6)

Ms的方向与股绳绕绳轴线的力矩M方向相反。当钢丝绳有多层股绳，股绳由多层丝组成时，根据式(1)、式(6)，可求得交互捻钢丝绳总扭矩为

(7)

当m=1、k=1时，式(7)可简化成由单层股绳、股绳由单层丝组成的交互捻钢丝绳的总扭矩，也即

(8)

对于单层股绳、股绳由单层丝组成的交互捻钢丝绳而言，n=n1且ns=ns1，有

M=Frtanα-Frstanβ

(8′)

式中符号同前。

2.3 同向捻钢丝绳

同向捻钢丝绳受拉时，其股绳中钢丝受拉时的受力及其对绳中心线的扭矩分析如图4、图5所示。M′s在垂直于钢丝绳轴线的分量Ms的方向与股绳绕绳轴线的力矩M方向相同。根据交互捻的推导过程，可得出有多层股绳、股绳由多层丝组成的同向捻钢丝绳总扭矩为

图4 同向捻受力分析图

图5 同向捻力和扭矩分解图

(9)

当m=1、k=1时，式(9)可简化成由单层股绳、股绳由单层丝组成同向捻钢丝绳的总扭矩，即

(10)

对于单层股绳、股绳由单层丝组成的同向捻钢丝绳而言，n=n1且ns=ns1，有

M=Frtanα+Frstanβ

(10′)

式中符号同前。

2.4 钢丝绳扭矩通用解

钢丝绳受拉时，其扭矩与承受的荷载通过一个恒定的扭转系数相联系，即

M=CQDF

(11)

式中符号同前。

实践表明，就多绳提升竖井而言，减小提升容器扭转位移的有效措施是采用偶数根捻向相反的钢丝绳或不旋转钢丝绳作提升钢丝绳。

当采用偶数根捻向相反的钢丝绳时

M′=±0.15ntCQDF′

(12)

当采用奇数根捻向相反的钢丝绳时

M′=±[1+0.15(nt-1)]CQDF′

(13)

式中：nt——提升钢丝绳根数；

M′——多绳提升钢丝绳总扭矩，kN·m；

F′——单根钢丝绳所承受的载荷。

其余符号同前。

3 钢丝绳扭转系数

3.1 扭转系数计算

提升钢丝绳扭转系数对计算提升容器最大水平摆动位移至关重要。通过对特定结构的钢丝绳扭转系数进行研究，分析钢丝绳扭转对安全间隙的影响程度，为钢丝绳选用提供参考。

以34×7右交互捻结构为例，假设：①荷载由各层股绳均匀承担，再由股绳均分到其各层钢丝上；②钢丝绳是一个杆件结构。外层股绳捻矩倍数ξ3为6.5倍，右交互捻，n3=17股；中层股绳捻距倍数ξ2为6.0倍，左同向捻，n2=11股；内层股绳捻距倍数ξ1为7倍，右交互捻，n1=6股。股绳为1+6，ns=7，ns1=6，股绳的捻距倍数ξs为8.5倍。

(14)

(15)

由式(14)可计算各层捻角：α1=17.211 9°，α2=23.316 6°，α3=23.173 6°，β1=14.155 3°。

由式(15)可计算各层捻制半径：r1=1.023 6φ，d=3.047 2φ，R3=2.955 2d=8.995 9φ，R2=1.920 5d=5.852 1φ，R1=1.035 4d=3.155 1φ。

将上述数据分别代入式(7)、式(9)有

同理可求出18×7右交互捻钢丝绳扭矩M=0.689 6Fφ；6×7右交互捻扭矩M=0.797 2Fφ，φ为钢丝的直径。

由式(11)，可求得各钢丝绳扭转系数，系数见表1。

表1 钢丝绳扭转系数表

根据表1中扭矩的计算公式可知，对于特定结构的钢丝绳而言，其扭转系数可用其钢丝直径与钢丝绳直径的百分比表示。表1中的扭转系数是在理想化结果。当钢丝绳提升高度不大时，可以用该结果计算提升容器的扭转位移。当提升高度足够大时，钢丝绳受外部荷载和使用工况的约束，其结构在提升过程中发生了不同程度的改变，扭转系数为变值。表1中的扭转系数计算公式可以拟合成通用解

(16)

选定钢丝绳规格后，由式(16)知，钢丝绳扭转系数与系数k成正比。系数k大小取决于钢丝绳结构及其捻角。

当采用偶数根捻向相反的钢丝绳时

M′=±0.15ntkF′φ

(17)

当采用奇数根捻向相反的钢丝绳时

M′=±[1+0.15(nt-1)]kF′φ

(18)

根据提升系统终端载荷确定了钢丝绳规格和根数后，由式(17)、(18)知，提升钢丝绳扭矩与其结构及捻角有关，通过选择合理的钢丝绳结构及生产工艺可减小提升同容器的水平摆动位移，降低其对提升容器安全间隙的不利影响。

3.2 钢丝绳结构的影响分析

由上述扭转系数计算可知，多层股钢丝绳外层股绳的扭矩比内层股绳的大。当提升钢丝绳承受载荷时，其必然朝外层绳捻向的反方向进行旋转，外层股绳相对伸长。由于提升钢丝绳的两端受约束，内、外层股绳间不能相互错动，导致外层股绳被迫凸起，内外层股绳分离，严重时会破坏钢丝绳结构，内层承受过多的载荷，钢丝绳使用寿命降低。若钢丝绳内有捻制应力，无法达到无差异受力状态时，内外层分离更加严重，甚至会造成钢丝绳未使用便报废。

针对钢丝绳结构构造及生产工艺，众多学者提出了许多措施，主要包括[1-3]：①消除钢丝绳捻制应力，使内外层不松散；②在不影响钢丝绳性能的前提下，抑外提内，平衡内外层扭矩；③优化钢丝绳结构，使钢芯与内外层股绳捻距相匹配，三者协调变形，避免钢芯早期断丝；④优化外层股绳的预变形量、内层股绳的直径，确保外层股绳微松散长度和回缩量均符合规定，并及时根据使用效果进行调整；⑤对内层股绳进行涂塑，防止内层股绳钢丝断裂；⑥采用改进型钢丝绳结构。比如用17×7/28×7+NF代替34×7，前者扭转系数为0.027，与后者相比降低了47%。通过钢丝绳结构的调整，扭转系数有了较大幅度的减小。

为了实现钢丝绳的多种性能，国内外进行了大量的研究。但目前钢丝绳关键术仍然只有少数外企掌握着，比如多层股阻旋转钢丝绳关键技术，出于利益考虑，这些关键技术未被市场化，这些非标钢丝绳结构均未列入技术标准，普及性受到限制。另外非标钢丝绳结构技术各不相同，且结构差别大，如Bridon以3层股组绳，而Redaelli、Kiswire则主要采用4层股组绳。

考虑到结构对钢丝绳抗旋转性能的重要影响，国际标准ASTM A1023/A1023M- 2007从组绳外层股数、组绳股层数和合绳次数将抗旋转钢丝绳又细分为3类：①稍微表现出有一定抗旋转性能；②表现出具有明显抗旋转性能；③表现出优异抗旋转性能即不旋转钢丝绳。

钢丝绳的性能受钢丝材质、股绳断面、捻制方式、防腐工艺、使用环境、更换方式和保养情况等方面的影响，其扭矩计算模型的理想化假设条件根本无法实现，在提升过程中钢丝绳结构不断发生变化，所以扭转系数在提升钢丝绳不同位置处为变值，因而很难通过纯粹理论计算准确求得钢丝绳的扭转系数。

3.3 钢丝绳捻角的影响分析

钢丝绳因股绳捻角而产生扭矩，进而扭转，扭转效应的强弱用钢丝绳每米的旋转程度即扭转系数表示。由式(7)、式(9)可知，扭矩与股绳捻角成正比，故当捻角减小时，扭矩也减小，钢丝绳承受的载荷在提升容器运行到某一位置时是恒定的。研究表明[4-5]，理想情况下，提升钢丝绳的扭转位移曲线为抛物线型，提升高度最顶底端处为零，在1/2提升高度处最大。但实际上钢丝绳最底端有一定的扭转位移，使得在>1/2提升高度处产生的位移接近上述扭转位移最大值，经研究，该处的罐道钢丝绳刚性系数最小，该分析与提升容器的最大水平摆动位移公式Umax=Fmax/Kmin是吻合的。此时的提升钢丝绳处于内外层钢丝受力差异最大的状态，此时钢丝绳的捻角接近最小。由式(11)、式(16)分析可知，扭转系数与股绳捻角成正比，故扭转系数的变化趋势与实际扭转位移的变化趋势一致，即在罐道钢丝绳刚性系数最小的位置处，提升钢丝绳的扭转系数也最小。

由于提升钢丝绳最底端的扭转位移无法准确确定，且其结构、生产工艺及使用环境差异性大等因素影响，故而在实际工程应用中无法对其不同位置处的扭转系数进行准确计算，给钢丝绳选用造成一定的困扰。

3.4 扭转系数对安全间隙的影响分析

目前，在阻旋转钢丝绳方面，国内虽然已掌握相应的技术，但是其扭转系数尚未解决，只能以普通钢丝绳扭转系数作参考。但国外在阻旋转钢丝绳关键技术及准确确定其扭转系数方面均领先于国内[6]。

提升容器扭转位移为

(19)

式中：Smax——扭转引起的容器最大位移，m；

Lmax——提升容器中心至其角点的最大距离，m。

由式(12)可知，钢丝绳的扭矩与扭转系数成正比，由式(19)可知，在一定的扭转角度内，扭转位移与扭矩成正比，即与扭转系数成正比。扭转系数越大，其对提升容器的安全间隙影响也就越大。

通常实测的钢丝绳扭转系数和表1的理论计算结果相近，分析认为表1及实测的数值均是钢丝绳的平均扭转系数，钢丝绳的实际扭转系数在钢丝绳的不同位置处是一个变值，故而无法直接计算钢丝绳的最大扭转位移。

进一步分析式(12)可知，即使采用偶数根捻向相反的钢丝绳时，提升系统仍然会有扭矩产生，总扭矩并不是零。从理论上讲，若能保证提升容器的各提升钢丝绳性能一致，通过多绳摩擦提升钢丝绳的布置形式可有效消除钢丝绳引起的扭矩。因而保证钢丝绳性能的一致性是提高钢丝绳使用效果、降低其扭转对安全间隙影响程度的重要手段。

4 结论

(1)由于钢丝绳的结构特点，在受到外部拉力时钢丝绳便会发生扭转，由此产生的扭矩不平衡导致提升设备发生偏移。但由于钢丝绳的复杂结构，不同厂家的工艺差异、钢丝绳的材质、不同绳股断面等因素的影响，无法准确的计算出钢丝绳的扭转系数，试验手段是对理论计算的弥补。

(2)实际应用中，受钢丝绳受力结构的影响,外层钢丝受力大于内层钢丝，非均匀受力，且不同位置处的钢丝绳会出现不同的受力差异，在接近1/2提升高度的位置此受力差异性最大，也即提升钢丝绳的扭转系数不是理论上恒定值，而在不同位置处呈现不同的数值，在钢丝绳内外层钢丝受力最不一致处，其扭转系数最小。

(3)相对于钢丝绳的扭转系数对设备扭矩的影响，钢丝绳间性能的稳定性、一致性对提升设备扭矩的影响更大，所以要加强钢丝绳的订货要求及管理。