局部散射理论在高超声速边界层转捩预测中应用的检验

2021-11-17李斯特

力学进展 2021年2期

李斯特董明

1 天津大学机械工程学院, 天津 300072

2 中国科学院力学研究所非线性力学国家重点实验室, 北京 100190

1 引言

对边界层转捩的有效预测是高超声速飞行器设计中的基础难题. 在环境扰动强度较低的“自然”状态下, 存在三个与转捩预测相关的基本问题(Kachanov 1994, 周恒和张涵信 2017). (1)感受性问题: 描述自由流中扰动如何进入边界层并激发失稳模态的过程; (2)线性失稳问题: 描述失稳模态是如何在边界层中持续增长的; (3)转捩判据: 确定线性扰动累积到多大幅值时非线性转捩发生. 工程中最常用的转捩预测方法是eN法(Smith 1956, Cebeci et al. 1980, Su & Zhou 2009), 它主要基于线性稳定性理论定量地描述机制(2), 而把非线性转捩判据与由感受性机制决定的线性扰动初始幅值的比值当作人为参数处理. 该理论的优点是简单易用, 但也存在明显不足: 首先, 该方法没有考虑机制(1)与(3)的影响, 故人为参数的确定较为随意; 更重要的是, 工程实际中飞行器表面很难做到完全光滑, 那里往往存在如粗糙元、缝隙、台阶等局部突变, 而它们对转捩的影响是传统的eN法无法考虑的. Schneider (2008a, 2008b)和Wheaton 等 (2010)的实验表明, 较大尺度的粗糙元可以促进超声速边界层转捩; 而Fujii (2006)和Fong 等 (2014)分别通过实验与直接数值模拟(direct numerical simulation, DNS)发现二维粗糙元在一定条件下可以使转捩推迟.Tang 等 (2015)通过风洞实验方法研究了高超声速边界层中第二模态扰动在二维粗糙元附近的快速畸变过程. 为了揭示粗糙元对转捩的影响机理, 需要进行更精细的理论研究工作. Wu 和Dong (2016)指出, 当失稳模态的波长与局部突变的流向尺度相当时, 线性稳定性理论与eN法均失效, 为此, 他们构建了一套新的理论框架−局部散射理论. 在该文章中, 他们关注的是亚声速机制, 之后该理论被推广到跨声速机制(Dong 2020)以及超声速与高超声速机制(Zhao et al.2019, Liu et al. 2020, Dong et al. 2020, Dong & Zhao 2021). 实际上, 局部突变对转捩的影响主要存在两个机理, 分别是局部感受性(局部突变与自由流中的扰动相作用而激发额外的失稳模态)与线性模态的局部散射(局部突变与来流失稳模态相作用而改变后者的幅值). 董明(2020)曾对局部散射理论在以上两种机制下的研究进展进行了系统的综述. 针对二维凹槽型局部突变, Dong和 Li (2021)还对这两种机制下线性扰动的演化开展了细致的直接数值模拟, 并把结果与理论进行了系统地对比. 但是该模拟只局限在层流阶段, 并未包含扰动的非线性转捩. 本文拟设计一个直接数值模拟方案: 假设高超声速边界层中已有失稳模态被激发, 计算它们在一系列粗糙元的影响下触发转捩的过程, 并把数值结果与理论预测进行细致地对比, 以验证局部散射理论在转捩预测中的精度.

2 物理问题与数值方法

本文选取的物理模型为带粗糙元的高超声速平板边界层, 如图1所示. 来流条件与Fong 等(2014)、Zhao 等 (2019)和Dong 和 Zhao (2021)相同, 马赫数 Ma、来流温度与单位雷诺数分别为 5.92, 4 8.69 K和 1.32×107m−1. 假设壁面存在三个流向孤立、展向均匀分布、形状相同的粗糙元, 它们到平板前缘的距离分别为 125.3 mm, 185 mm和 244.7 mm.

以第二个粗糙元中心位置原点建立笛卡尔坐标系. 通过可压缩光滑平板边界层的Blasius相似性解可以估算出该处的排移厚度本文选取这个值作为无量纲化的参考长度. 这样, 三个方向的无量纲坐标为其中上标 * 为有量纲值. 三个粗糙元中心的无量纲坐标分别为x1=−30,x2=0,x3=30. 令每个粗糙元的形状分布为h和d分别标识每个粗糙元的高度与宽度. 在本文的计算中,h=0.24,d=2.37 . 在计算中布置贴体网格, 如图2所示, 并建立贴体坐标系 (ξ,η,ζ). 计算域取−42.65≤ξ≤230.65, 0≤η≤50, 0 ≤ζ≤23.64 , 计算网格数为 2129×151×128. 各物理量均以来流参量进行无量纲化, 进而定义雷诺数其中u∞和ν∞分别为来流流向速度与运动黏性系数.

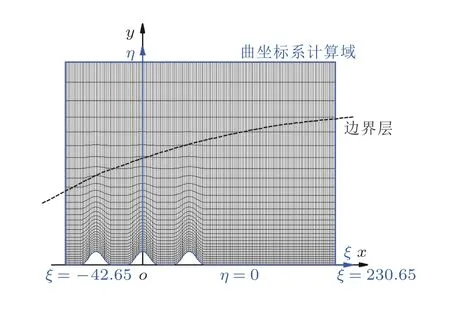
图2

物理模型示意图

控制方程为贴体坐标下的三维可压缩Navier−Stokes方程组, 采用有限差分法对其离散. 在计算基本流时, 对流项采用五阶WENO (weighted essentially non−oscillatory)差分格式, 黏性项采用四阶中心差分格式, 时间推进采用LU−SGS (lower−upper symmetric Gauss−Seidel)方法; 在计算扰动时, 对流项采用五阶迎风差分格式, 黏性项采用六阶中心差分格式, 时间推进采用三阶Runge−Kutta法, 具体离散过程见赵磊 (2017). 首先计算二维定常基本流, 即在图1的三维计算域中选择一个z=0的切片. 计算域入口给定为可压缩Blasius解, 上边界和出口采用外推边界条件, 壁面为无滑移、无穿透、等温的边界条件, 其中无量纲壁面温度Tw为 6.88. 二维基本流计算定常后, 把它展向均匀地布置在三维计算域中, 计算三维转捩过程. 在入口引入 5个特征模态扰动,形式为其中下标i表示第i个扰动;分别表示密度、流向速度、法向速度、展向速度和温度的特征函数;ω为频率,β为展向波数,A为扰动初始幅值,c.c.表示复共轭. 在三维非定常数值模拟中, 上下边界条件与计算基本流时相同, 但出口改用嵌边边界条件, 以保证扰动无反射地传出计算域. 展向采用周期边界条件. 在给定的ω和β下 ,qˆ由可压缩Orr-Sommerfield (O-S)方程给出. 在本文计算工况中, 选取的5个模态扰动的参数如表1所示.图3展示了计算域入口处, 不同频率扰动的增长率−αi, 图中的“°”标识本文引入的扰动. 为定量刻画粗糙元对转捩的影响, 本文计算了光滑平板与带粗糙壁面的两种工况, 分别标记为Case 1与Case 2.

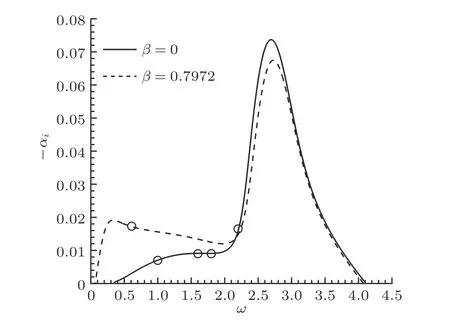
图3

表 1 模态扰动参数

3 散射理论的应用检验

图4为Case 2的平均流压力的等值线云图. 每个粗糙元对平均流的修正在无黏势流区表现为压缩−膨胀波系, 其马赫角为 tan−1(Ma2−1)−1/2≈10°.图5进一步展示了x=0附近的压力等值线云图和流线, 可以清楚地看到在粗糙元上游的高压区与下游的低压区, 流线也在凸起附近明显弯曲, 但在粗糙元前后均未出现分离, 其他粗糙元附近的流场也类似. 从定量上看, 该结果与Zhao 等 (2019)文中的图4(c) 吻合很好. 在距离突变足够远的上下游, 平均流也趋近于未受扰动的Blasius解.

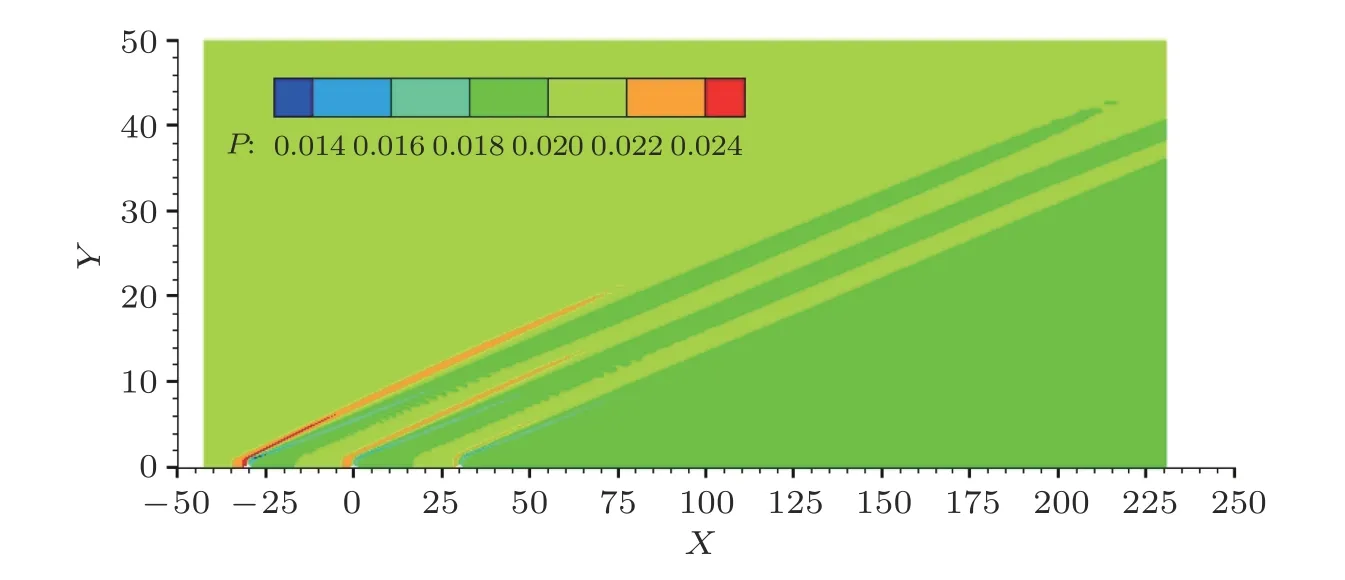
图4

图5

对于亚声速边界层中的黏性Tollmien−Schlichting (T-S)模态, 粗糙元往往促进扰动的增长,从而使转捩提前(Wu & Dong 2016); 但在高超声速边界层中, Fujii (2006)通过实验发现了相反的结论. 加州大学洛杉矶分校的Zhong课题组的一系列数值工作(Duan et al. 2013; Fong et al. 2014,2015)表明, 粗糙元只会促进频率低于同步频率的扰动增长, 而对高频扰动有抑制作用. Zhao等 (2019)采用求解谐波型线性化Navier−Stokes方程(harmonic linearized Navier−Stokes equation, HLNS) 在马赫数为5.92工况下, 对透射系数与来流扰动的频率、展向波数以及粗糙元大小和位置的关系进行了系统的数值计算. Dong 和Zhao (2021)采用高雷诺数渐近理论, 对该现象给出了深刻解释. 本文的DNS可进一步展示该机制对非线性转捩阶段的影响.

对由DNS得到的流场进行傅里叶变换

其中qˇn,m(x,y)为频率为mω0、展向波数为nβ0的 Fourier分量,ω0=0.2为基频,β0=0.7972为基波数,T=2π/ω0为时间周期,ZK=6π/β0为展向计算域长度,q˜(x,y,z,t)为瞬时扰动量.图6给出了光滑壁情况下典型第二模态扰动(表1中的扰动3, 4和5, 它们所对应的 (m,n) 分别为(8, 0), (9, 0)和(11, 0))的傅里叶分量的幅值(傅里叶分量的模的法向最大值)与线性稳定性理论预测结果的对比. 可以看出在x= 0以前, 幅值最大的扰动(11, 0)几乎线性增长, 在幅值达到0.01的量级后进入非线性饱和阶段. 而扰动(8, 0)和(9, 0)在下游可以累积到更大的幅值, 最大幅值的扰动(8, 0)的幅值峰值达到了0.042.图7中的虚线展示了更多频率下的傅里叶分量在更宽的流向区域内的演化规律. 高频第二模态(m= 8, 9, 11)在非线性饱和后迅速衰减. 低频的第一模态(m= 1, 2, 3)在前期增长率较低, 但它们可以持续增长到x=130左右. 在x=180以后, 各阶扰动的脉动强度趋于稳定, 它们的幅值在0.01到0.02之间波动, 这说明转捩即将完成. 这一过程与Dong 和 Luo(2007)对高超声速尖锥边界层自然转捩的规律相同: 由于第二模态的线性增长率较高, 它们是转捩前的主导扰动; 但是, 只有三维的低频模态的幅值累积到非线性状态的时候, 转捩才能被触发;第二模态对第一模态的增长起到“催化”作用.

图6

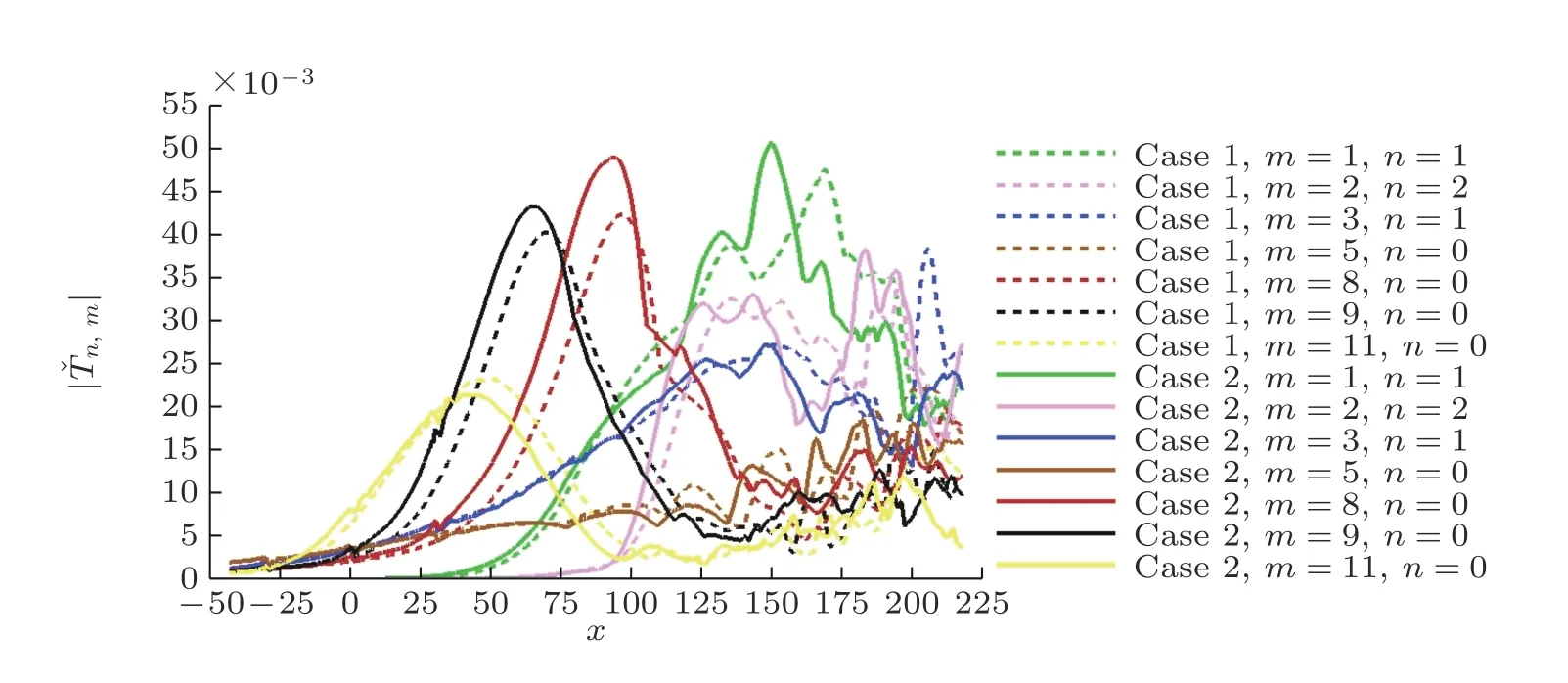
图7

图7中的实线表示Case 2的结果, 它们与Case 1的主要区别是: 在粗糙元附近, 扰动的幅值存在明显的“跳跃”, 这进一步影响扰动在下游的演化幅值. 引入透射系数T(Wu & Dong 2016)来量化这一跳跃, 其定义为下游与上游渐近幅值之比, 这里的渐近幅值可通过Case 1的结果得到.对于每个频率、展向波数组合 (m,n)的扰动, 在三个粗糙元处的透射系数记作T1(m,n),T2(m,n)和T3(m,n).

Zhao 等 (2019)通过HLNS, 得到相同马赫数和Reδ0∗= 26 307工况下的透射系数随频率的分布. Dong 和 Zhao (2021)进一步用渐近理论讨论了这一结果受Re的影响. 实际上, 本文中三个粗糙元所处位置对应的雷诺数Reδ0∗分别为21 648, 26 307和30 228; 而从Dong 和 Zhao (2021)的结果来看, 这三个雷诺数所对应的T~ω曲线非常接近.图8给出由DNS数据读出的n=0, 不同频率下的T1,T2与T3; 这里对频率重新归一化, 此处所采用的特征长度为粗糙元中心处对应的光滑平板边界层排移厚度. 图中还画出HLNS的结果(选自Zhao et al. 2019)做对比, 它们总体吻合很好. 另外, 在HLNS计算中, 扰动被假设为线性的, 但在实际DNS中, 有些扰动已经达到了非线性状态(幅值O(0.01)). 但是两者仍然能给出较一致的透射系数, 这说明非线性效应在局部散射过程中作用较弱. 而即使扰动发展到弱非线性阶段时, 粗糙元对扰动的局部散射效应仍可近似被透射系数描述.

根据局部散射理论(Wu & Dong 2016, Zhao et al. 2019, Dong & Zhao 2021), 对于有k个局部突变的平板边界层, 透射系数与转捩阈值的变化 ΔN存在对应关系通过观察DNS计算出的扰动幅值演化(图7)发现ω=1.6,β=0 (m= 8,n= 0)的模态在转捩前占主导地位, 这与基于线性稳定性理论的eN方法给出的结论相同. 通过该模态在三个粗糙元处的透射系数可以算出转捩因子的变化值 ΔN=0.3736. 在传统的转捩预测eN法中, 当最危险的扰动根据线性理论放大eN倍时, 认为转捩发生. 而对于存在粗糙元的工况, 需要用由透射系数确定的 ΔN修正转捩因子, 并认为当最危险的线性扰动首次放大 eN−ΔN时转捩发生. 根据eN法, 按扰动由线性过渡到饱和状态的幅值选取转捩因子N. 对于本文工况, 选取的N值为3.23, 进而读出Case 2曲线相对与Case 1曲线的前移量 Δx≈9, 这就是局部散射理论预测的转捩前移量.

图9给出了壁面摩阻系数沿流向的变化. 对于光滑壁面的工况(Case 1),Cf曲线先缓慢减小,再从x=113.5 处开始剧烈升高. 对于Case 2,Cf曲线在粗糙元附近有较明显下降, 但在不远的下游向未受扰动的状态恢复. 在本文模拟的工况中, 粗糙元促进了失稳模态的增长, 这使得Cf曲线剧烈抬升的位置有所提前. 若把Cf曲线最低点看作转捩的起始点, 则粗糙元的存在使转捩提前了Δx≈7. 这与理论预测的转捩前移量非常接近, 从而说明了局部散射理论的可靠性.

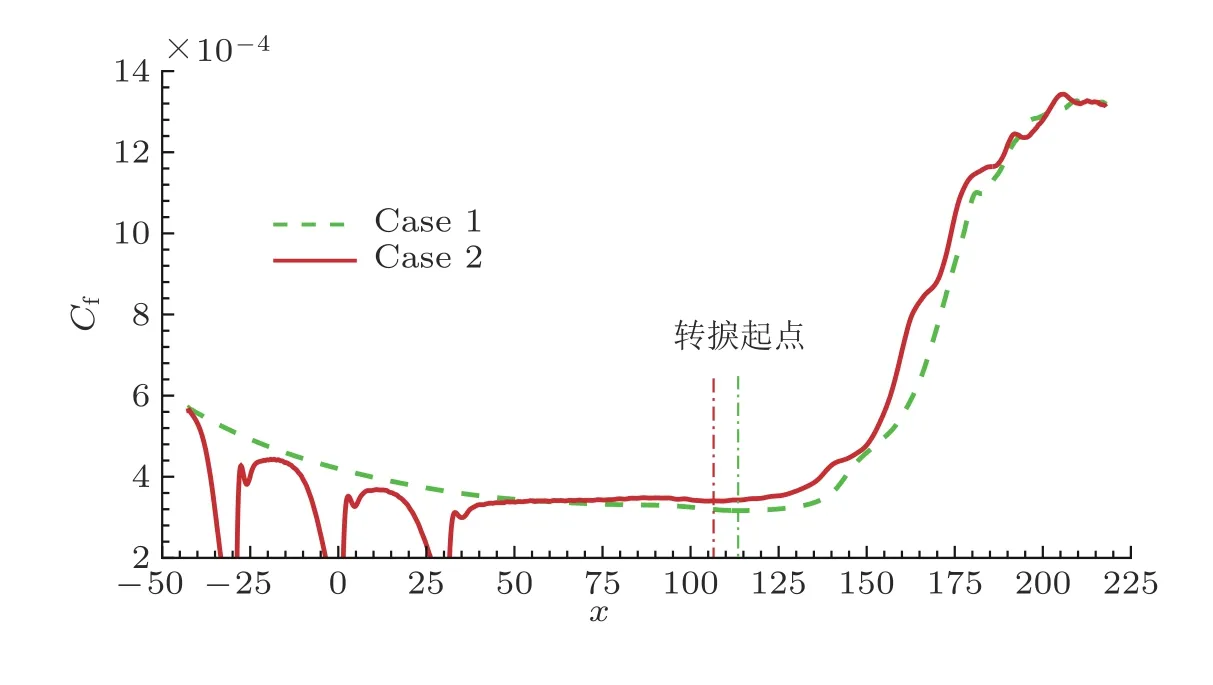
图9

4 结论

为了验证局部散射理论在高超声速边界层中转捩预测的精度, 本文设计了一套直接数值模拟工况: 分别在光滑壁面与包含若干粗糙元的高超声速边界层中引入相同的初始失稳模态, 以定量考察粗糙元对转捩的影响. 得到如下结论:

(1) 通过对比两个工况下扰动傅里叶分量的演化规律, 定量刻画了粗糙元对扰动演化的影响,该结果与局部散射理论的预测基本吻合. 同时, 数值结果进一步表明, 虽然局部散射理论假设扰动是线性的, 但其结果也可以近似应用于描述扰动在弱非线性阶段的演化.

(2) 通过透射系数可以定量计算主导模态扰动的转捩因子的变化值, 进而确定其对扰动幅值累积的影响. 由该机制得到的转捩位置的变化量得到了直接数值模拟的验证.

值得说明的是, 本文模拟的工况中, 由粗糙元引起的转捩的提前量较小. 这是由于本文设计的粗糙元较少, 且每个粗糙元的高度较低. 在真实应用中, 更多更大尺寸的粗糙元可使转捩前移更加明显. 同时, 巧妙地设计粗糙元, 使得主导扰动的频率尽量落在图8的高频区, 是有可能使转捩推迟的, 这将是作者下一步的工作.

附录A

对本文直接数值模拟精度的验证

由于风洞实验中的背景扰动不易确定, 很难把数值结果与实验结果做细致对比. 为了验证本文计算的可靠性, 首先对计算网格进行验证. 保留本文计算的网格宽度, 把流向计算域缩短为x∈[−42.6,107.9],计算网格数变为1201×151×128. 为了使流动在更短的距离转捩,初始扰动((ω,β)=(0.5,0.7972), (1.0,0)和 (2.5,0)) 的幅值被增大为 0.01. 同时计算了网格数为 2401×151×128和1201×151×256 的流场, 并把三套网格下计算出的Cf曲线进行对比, 如图A-1所示. 可以看出, 流向网格的加密对计算结果没有影响, 而展向网格的加密使转捩后期及湍流区的Cf值略大. 由于本文更关注的是转捩前的局部散射作用与转捩起始位置, 所以可以认为本文计算网格达到精度要求. 此外,选取Zhao 等 (2019)中图9 (d)的工况, 重新计算了扰动的流向演化, 其扰动温度如图A-2所示. 两条曲线精确吻合. 以上验证说明了本文的计算结果是可靠的.