曲面薄膜结构褶皱失稳力学
2021-11-17杨易凡
徐 凡 杨易凡 汪 婷
复旦大学航空航天系力学与工程仿真研究所, 上海 200433
1 引 言
薄膜结构在自然界和现代工业中广泛存在 (见图1). 由于其具有质轻、二维、高柔度、可伸展和高收纳比等特性被广泛应用于航空航天和建筑工程, 例如大面积太阳电池阵、薄膜翼、充气天线、太阳帆、再入减速装置、太空舱和水立方膜结构等(杜星文等 2006, 王长国等 2007, 胡海岩 2016, 彭福军等2017). 然而, 薄膜由于面外抗弯刚度较低(量级为厚度的三次方), 而面内刚度相对较高(量级为厚度的一次方), 因此, 薄膜结构易发生面外变形、失稳和褶皱. 受限薄膜和薄壳等薄壁结构通过丧失面外稳定性(起皱)来降低面内的拉伸/压缩能, 通常被认为是走向灾难性破坏的途径(Bažant 2000, Wang et al. 2016, 曹进军等2019, Luo et al. 2020). 从另一方面看, 随着极端变形材料和柔性结构的兴起和应用(Li et al. 2012, Reis et al. 2018, Reis 2015), 可以反过来利用这种屈曲失稳行为实现特定的功能, 例如通过可编程的起皱纹理形成伪装皮肤(Pikul et al.2017), 引入微结构的褶皱区域定位(Yan et al. 2014), 利用拓扑优化的无褶皱设计(Luo et al.2017), 软体驱动的形貌控制(Siéfert et al. 2019), 自主驱动的分岔引导打印(Jiang et al. 2019), 形状可编辑的多稳态超表面(Bende et al. 2015), 褶皱斑图地貌的动态调控(Paulsen et al. 2016)以及自适应气动性能控制(Terwagne et al. 2014)等. 可逆的失稳响应操控, 尤其是屈曲和稳定状态之间的灵活过渡, 将是相关功能性应用的关键, 可为几何拓扑相关的功能性薄膜结构的智能制造提供指导, 具有广阔的应用前景.
平面薄膜结构的褶皱失稳形貌在各个面内尺度下较为相似, 表现为无尺度效应(见图1 (a)~图1(e)).然而, 初始曲率影响下薄膜结构的变形失稳形貌却较为复杂(见图1 (f)~图1(j)), 与平面构型下的褶皱斑图存在明显差异, 反映出曲率的作用效果. 软膜−硬基底系统中的曲率可以引导缺陷自组装, 例如裂纹扩展路径(Mitchell et al. 2017)和褶皱形貌(Irvine et al. 2010, Ma et al. 2019, Janssens et al. 2020). 曲率在核壳结构(Li et al. 2011; Zhao et al. 2014; Xu & Potier-Ferry 2016; Xu et al.2017, 2020b; Zhao et al. 2021)和膜基系统(Cai et al. 2011, Yang et al. 2018, Xu & Zhao 2020, Zhao et al. 2020, Ding et al. 2021)的褶皱模态选择和形态转化中起关键作用. 自发曲率会导致薄壳旋转对称性破缺和跳跃屈曲失稳(Zhang et al. 2018, Pezzulla et al. 2018). 另外, 曲率可延缓均匀生长系统中褶皱的形成(Jia et al. 2018). 在发育中的哺乳动物大脑沟壑形态的异质系统中, 曲率小的区域首先发生失稳(Budday et al. 2015). 结合曲率和剪裁设计可以实现波在折纸结构中的传播(Rafsanjani et al. 2019). 在拉伸作用下, 曲线丝状超结构网络可以使变形模式从拉伸到弯曲转变(Yan et al. 2020). 总之, 理解曲率对褶皱形貌演变和失稳模态成形的力学机理对于有效利用失稳实现智能表面等功能性用途至关重要.
本文针对曲面薄膜结构褶皱失稳行为, 从曲率影响下的薄膜拉伸稳定性和膜基结构表面失稳形貌选择两类问题的研究进展进行综述, 重点围绕曲率对失稳模态的影响及力学机理、模型与方法进行阐述分析, 最后对其发展趋势进行展望.
2 曲率影响下的薄膜拉伸稳定性
2.1 平面薄膜拉伸起皱临界
二十年前, Friedl等(2000), Cerda等(2002)以及 Cerda & Mahadevan (2003)相继揭示了单轴拉伸下平面薄膜会出现横向褶皱. 上述研究以及其他早期研究都受限于小应变(约1%)起皱行为, 研究对象通常是传统硬材料, 如金属和塑料薄膜. Friedl等(2000)给出了临界拉应力的表达式
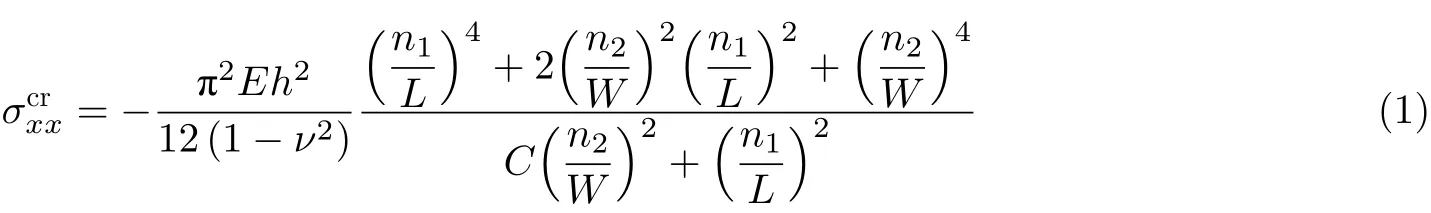
其中C=σyy/σxx为 比例系数,σyy为 长度方向的应力,σxx为 横向应力,L为 长度,W为宽度,h为膜厚,E为弹性模量,ν为泊松比,n1,n2分别是长度方向和横向的半波数. 随后, Cerda等(2002)以及Cerda & Mahadevan (2003)通过能量极小化原理推导出褶皱波长λ和 幅值A的标度律关系
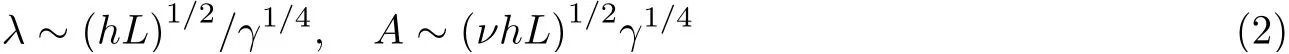
其中γ为拉伸应变. 进一步地, Jacques & Potier-Ferry (2005)基于稳定性理论, 解析获得了临界拉应力和横向失稳波长l的表达式
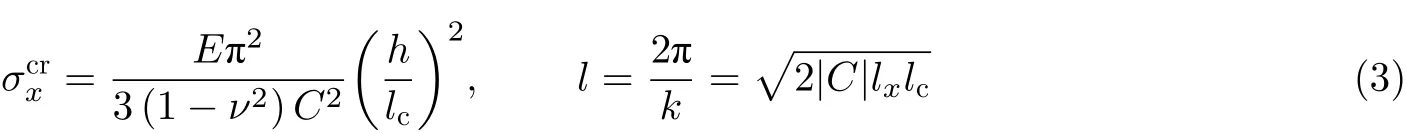
其中lx为 长度方向屈曲长度,lc为特征长度,k为横向失稳波数. 随后, Kim等(2016)和Puntel等(2011)通过能量变分, 给出了临界拉伸应变的表达式
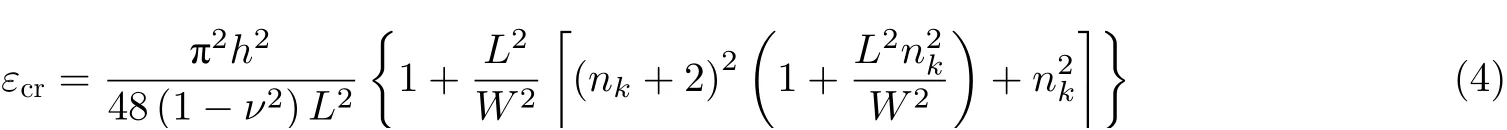
其中nk∈N.
2.2 平面超弹性薄膜拉伸起皱与再稳定
随着软物质力学的发展(冯西桥等2017, Reis et al. 2018), 非线弹性有限变形理论得到广泛应用. 同时, 人们开始利用软材料大变形和失稳突变等特性实现形貌调控等功能性用途. Zheng(2009)首次发现了过度拉伸的超弹性薄膜中的再稳定(平整化)行为, 即随着拉伸的持续增加, 薄膜褶皱幅值先增加、后减小, 最后消失(ε~ 0.3), 如图2所示. 这是软薄膜大变形后出现的孤立中心分岔(isola-center bifurcation)行为, 源自拉伸能与弯曲能之间的非线性竞争, 需要从解析、数值和实验上对其力学机理进行深入探究. 同时, 由于薄膜拉伸产生较大的面内变形, 经典的小应变板壳模型已不再适用, 需要发展新的板壳理论和计算方法来预报超弹性薄膜拉伸起皱与再稳定现象.
Healey等(2013)通过在Föppl-von Kármán (FvK)薄板几何方程中引入面内非线性变形梯度项, 提出了基于Saint-Venant Kirchhoff (SVK)本构的有限应变薄板模型. 其格林−拉格朗日应变张量表示为
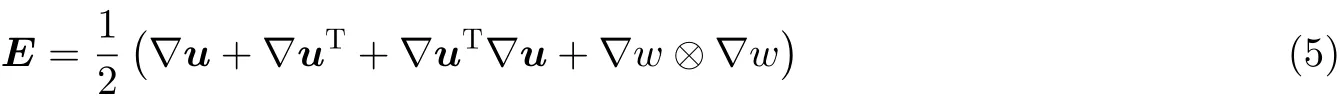
其中u和w分 别表示面内位移和面外挠度,∇(·)表 示二维面梯度,⊗表示张量积. 当忽略式(5)中的面内非线性项∇uT∇u, 则退化为经典的FvK板模型. 两种模型都采用了线性曲率. 通过能量变分, 最后可得平衡微分方程

其中N为板中面的第二Piola-Kirchhoff (PK)应力张量. 注意到面内平衡方程中, 不同于经典FvK板模型第二PK应力的散度为零, 此处SVK板模型是第一PK应力的散度为零. 利用欧拉−牛顿数值算法求解, 可得到挠度−应变演化分岔图2 (b). 结果表明SVK模型能预测起皱−消皱的孤立中心分岔行为, 而经典FvK板模型无法预报褶皱消失现象. 因此, 几何方程中的面内非线性项对褶皱的消失起着决定性作用. 进一步地, Li和Healey (2016)探究了材料非线性行为, 即neo-Hookean (NH)和Mooney-Rivlin (MR)超弹性本构对孤立中心分岔演化的影响. 结果表明可描述材料非线性行为的NH和MR模型在预测褶皱消失的再稳定点上比线弹性本构的SVK模型更精确. 然而, SVK模型仍足以捕捉到褶皱的出现和消失行为, 表明不同的超弹性材料本构模型并不会对这一孤立中心分岔行为产生质的影响, 说明该现象主要依赖于几何非线性.

图2
Fu等(2019)从三维超弹性应变能函数出发推导了多种二维薄膜超弹性本构模型, 提出了适用于多种可压缩和不可压缩超弹性本构及应变硬化材料的有限应变板模型, 采用基于连续摄动理论的数值渐近法与可处理空间微分离散的谱配点方法相耦合的数值计算框架, 准确预测了薄膜拉伸起皱−消皱的演化全景. Wang等(2019)基于Koiter稳定性理论, 首次半解析地预测了孤立中心分岔点, 探究了泊松比对薄膜拉伸起皱与再稳定的影响, 发现较小的泊松比会导致较滞后的褶皱出现、更低的失稳振幅和较早的褶皱消失行为. 特别地, 当泊松比低于一个阈值时, 薄膜在单轴拉伸时不会出现褶皱. 另外, 当薄膜长宽比大于4时, 薄膜中心起皱将分裂为两端起皱.
除考虑各向同性材料薄膜外, Sipos和Fehér(2016), Zhu等(2018), Liu等(2019), Yang等(2020)探究了各向异性材料对薄膜失稳行为的影响. Liu等(2019)发现改变材料主方向和拉伸方向的夹角可对褶皱方向进行定向调控. Taylor等(2019)探究了不可压纤维增强薄板在多种力学加载下的褶皱形貌. Yang等(2020)通过在大应变板理论中引入各向异性超弹性本构, 建立了各向异性超弹性有限应变板模型, 发现当纤维与基质的剪切模量比高于临界值时, 褶皱消失, 即薄膜在拉伸过程中保持表面平展.
2.3 曲面薄膜稳定性与曲率消皱机制
薄膜结构通常具有曲面几何构型, 自然而然引出一些科学问题: 曲率是否影响褶皱失稳发生发展? 薄膜起皱是否依赖于初始曲率? 曲率能促进亦或是抑制薄膜起皱行为?
Wang等(2020)发现曲率可以有效且精确地调控起皱与消皱行为(见图3). 当薄膜弯曲时(具有初始曲率), 不同于平面薄膜拉伸出现局部起皱现象, 曲面薄膜会出现局部起皱与整体弯曲的耦合变形行为. 且存在临界曲率, 当曲率大于阈值时, 薄膜拉伸时始终保持表面光滑, 不会出现褶皱, 即曲率可抑制褶皱发生. 为定量理解其内在力学机理和影响因素, Wang等(2020)基于广义曲线坐标系的微分几何, 建立了可以描述柱面的有限应变薄壳模型, 可准确预测薄膜起皱−消皱行为. 对于柱面几何, 采用弧长s和轴长z组成曲线坐标系 (s,z), 则柱面可以参数化为且其度量张量和曲率张量分别表示为
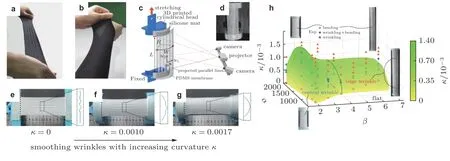
图3
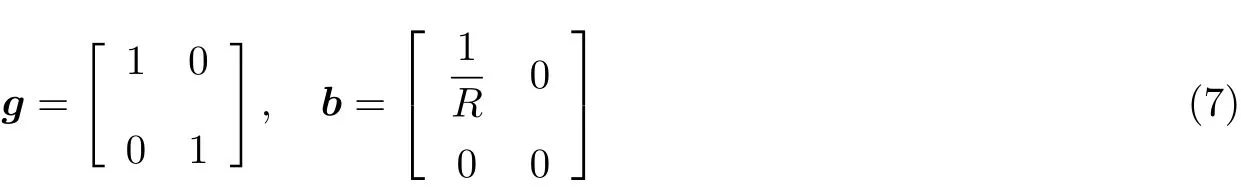
柱面下的格林−拉格朗日应变张量可以表示为
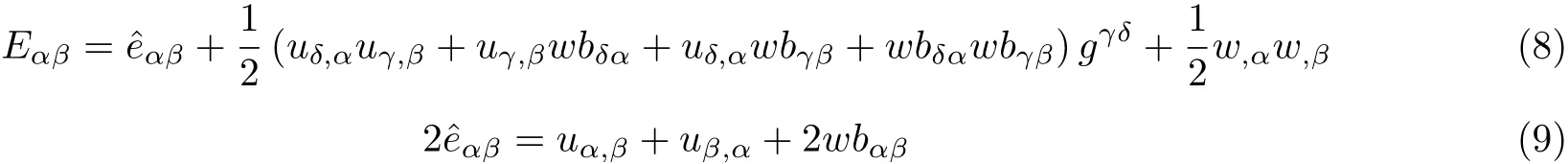
(1)小曲率:uδ,α~O(ϱ)和bγβ~O(ϱ2). 小曲率下柱面薄膜应变张量为
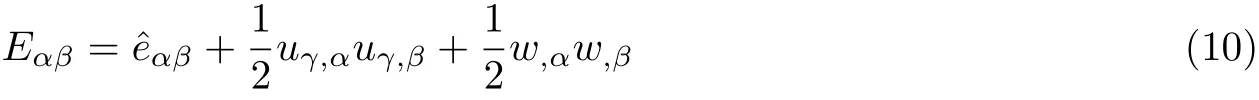
当第二项面内非线性项忽略时, 模型退化为经典Donnell-Mushtari-Vlassov (DMV)壳模型(Yamaki 1984).
(2)有限曲率:uδ,α~O(ϱ)和bγβ~O(ϱ). 有限曲率下柱面薄膜应变张量为

线性化的弯曲应变张量可表示为

其中ε12n,ε˜12n分别为参考和当前构型下基矢量的混合积. 假设短波失稳下发生适当的面外转动(法矢量转动较小), 则弯曲应变张量的非线性项可以忽略, 且近似有Bα=−w,α, 同时变形状态下度量张量近似为1. 相应地, 存在两种情况:
(1)小曲率:uδ,α~O(ϱ)和bγβ~O(ϱ2). 小曲率下柱面弯曲张量表示为

即为经典的DMV壳曲率假设(Yamaki 1984).
(2)有限曲率:uδ,α~O(ϱ)和bγβ~O(ϱ). 有限曲率下柱面弯曲张量为
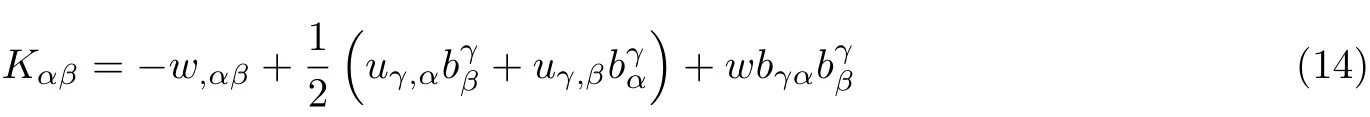
基于欧拉−拉格朗日方程, 最后可得有限曲率柱面薄膜的平衡微分方程组
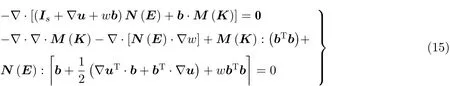
其中薄膜力N与弯矩M分别表示为
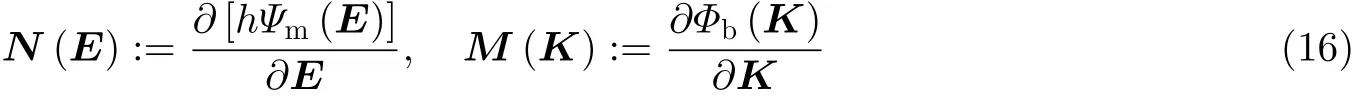
其中Ψm和Φb分别为薄膜能密度和弯曲能密度.
通过数值渐近法和谱配点法可定量求解方程(15)并预测追踪非线性失稳形貌演化全景(见图4). 对于平面薄膜(曲率κ=0), 在拉伸应变约2.5%时褶皱出现, 随着拉伸应变增加, 褶皱幅值先增大后减小, 最后消失, 整个路径即为孤立中心分岔演化. 对于曲面薄膜, 在拉伸过程中出现整体弯曲与局部起褶耦合的失稳行为, 且褶皱幅值随着曲率的增大而减小. 当曲率高于临界值时,薄膜不会出现褶皱, 只发生整体弯曲变形. 这可以从弯曲能和薄膜能的非线性竞争来理解(见图4 (b)).平面薄膜在拉伸过程中, 褶皱出现前其弯曲能保持为零; 褶皱出现后, 随着继续拉伸, 弯曲能先增加后减小; 当褶皱消失后, 弯曲能再次变为零. 对于曲面薄膜, 在拉伸过程中, 弯曲能一直处于主导, 始终增加, 且当初始曲率大于临界阈值时, 弯曲能不发生突变. 注意到经典DMV壳模型无法预报褶皱消失的再稳定点, 而Wang等(2020)提出的有限应变壳模型可准确预测曲面薄膜拉伸起皱−消皱行为. 理解曲率对软薄膜稳定性形貌演变对于有效利用褶皱作为形貌设计至关重要,也为薄膜结构平整化(消褶)提供了新的思路.

图4
3 曲率影响下膜基结构表面失稳行为
3.1 平面膜基结构
把薄膜铺在基底上, 则形成膜基结构. 软物质表面失稳现象, 即膜基结构表面起皱行为在自然界中普遍存在, 例如皮肤皱纹(Efimenko et al. 2005)、大脑沟回(Tallinen et al. 2016)、风干水果(Li et al. 2011)和花叶形貌(Xu et al. 2020a)等; 现代工业中, 膜基结构失稳行为在表面自清洁、防污损(Pocivavsek et al. 2018)、形貌伪装(Pikul et al. 2017)和微纳米斑图成形(Bowden et al.1998)等领域具有广泛应用. 然而, 如何定量预测并连续追踪后屈曲非线性失稳模态中的多重分岔转变仍是一项挑战.
由于薄膜褶皱波长λ通常远大于膜厚, 薄膜面内应变一般可用FvK薄板几何方程描述(Chen & Hutchinson 2004, Huang et al. 2005)
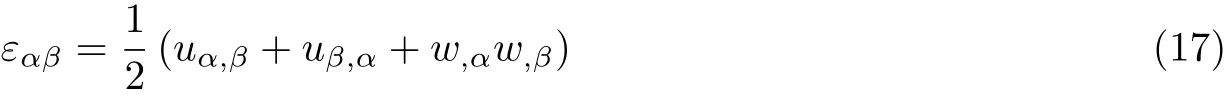
单轴压缩下, 膜基系统通常会在临界阈值处屈曲产生正弦形褶皱(Allen 1969; Biot 1963; Xu et al.2014, 2015; Xu and Potier-Ferry 2016), 此时薄膜力可表示为(Genzer & Groenewold 2006, Chung et al. 2011)
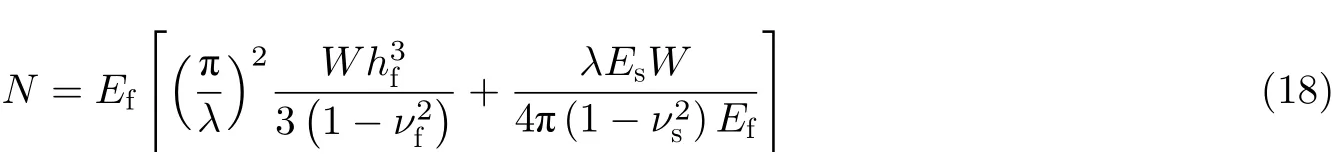
其中E为杨氏模量,ν为泊松比,hf为薄膜厚度,W为宽度, 下标f和s分别表示薄膜和基底. 应力极小化满足条件 dN/dλ=0, 可得到临界失稳波长λc


可以看到, 临界应变εc仅取决于模量比. 从能量角度看, 软基底上薄膜起皱是在薄膜弯曲能、拉伸能和基底的变形能之间寻求平衡的过程(Khang et al. 2006, Huang et al. 2005, Song et al. 2009,Fu et al. 2018). 当达到临界压缩应变时, 薄膜会发生屈曲从而降低系统的总势能. 考虑已经起皱的薄膜受到额外施加的应变(εappiled), Jiang等(2007)发展了一种有限变形框架下的模型用于预测褶皱波长和幅值
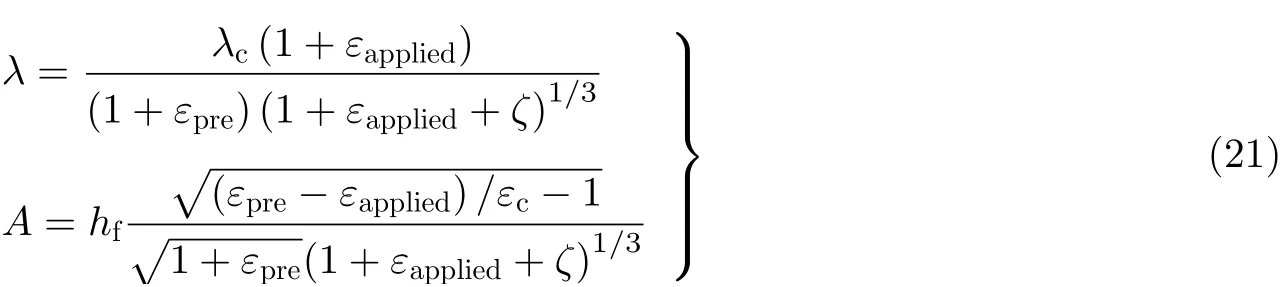
其中εpre为基底的预应变,ζ=5(εpre−εapplied)(1+εpre)/32. 式(21)提供了在额外施加应变下褶皱波长和幅值的预测.
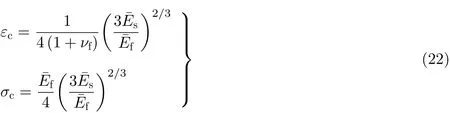
对于膜基结构受双轴压缩的情况, 临界应变εc和 应力σc与单轴压缩的理论解仅存在系数上的差异, 分别表示为(Audoly & Boudaoud 2008, Chen & Hutchinson 2004)
Zhao等(2015)探究了受限各向同性生长(膨胀)条件下, 横向尺寸对柔性基底上薄膜起皱的影响, 得到临界生长应变εg为
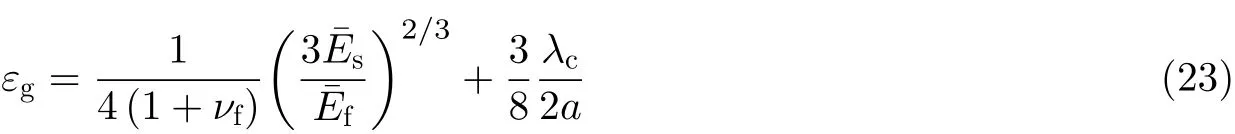
其中方形薄膜的宽度为2a. 式(23)表明除弹模比外, 方形膜基结构起皱的临界生长应变也依赖于临界波长和薄膜宽度.
对于模量比Ef/Es~5−1000范围内的膜基结构, 在临界失稳后进一步加载, 会出现倍周期模态(周期性的成对褶皱)的二次分岔失稳, 更进一步加载会导致四倍周期模态(Brau et al. 2011,Cao & Hutchinson 2012). 当系统存在结构缺陷、预拉伸或液体基底时, 还可能出现其他模态, 如三倍周期(Budday et al. 2015a, 2015b)、凸脊(Auguste et al. 2018, Cao & Hutchinson 2012)、多级褶皱(Cheng & Xu 2021)和自接触折痕(Pocivavsek et al. 2008, Sultan & Boudaoud 2008, Sun et al.2012)等复杂形貌(见图5).

图5
近年来随着膜基结构表面自组装技术的飞速发展, 各种薄膜材料包括无机物(Chen et al.2017)、金属(Bowden et al. 1998)、聚合物(Rodríguez-Hernández 2015)和新型碳材料(Hu et al.2019)被用于制造微/纳米结构. 驱动薄膜自组装的机械力可由化学反应(例如表面聚合和氧化)(Rodríguez-Hernández 2015)或物理刺激(例如热应变、预应变释放和光致变形) (Ohzono &Monobe 2012, Fu et al. 2018, Zhao et al. 2019, Zhao et al. 2021). 总之, 软基底上薄膜的起皱形貌、模态和特征尺度受多参数(例如薄膜和基底模量比、失配应变和应力分布等)影响(倪勇等2018). 早期的工作大多聚焦于平面初始构型下的膜基结构, 近年来越来越多的学者开始关注曲率对表面褶皱形貌的影响.
3.2 柱面膜基结构
本节讨论在各种载荷下(例如轴向压缩、热膨胀/收缩和体积增长)的柱面核壳结构表面起皱行为. 柱面和锥面都是具有零高斯曲率的可展曲面, 几何上属同一类曲面构型. 对于半径为R,外层厚度为hf(hf/R≪1)的柱面核壳结构, 经典DMV框架下(Yamaki 1984)的应变张量和曲率张量为
与平面膜基系统相比, DMV浅壳模型中环向应变多了曲率的贡献, 即w/R. 显然, 当柱面退化为平面时(R→∞) , 有w/R→0 , 几何方程与平面系统一致. 柔性核心刚度Ks取决于基底的弹模和屈曲半波长ℓx(Allen 1969, Biot 1963)

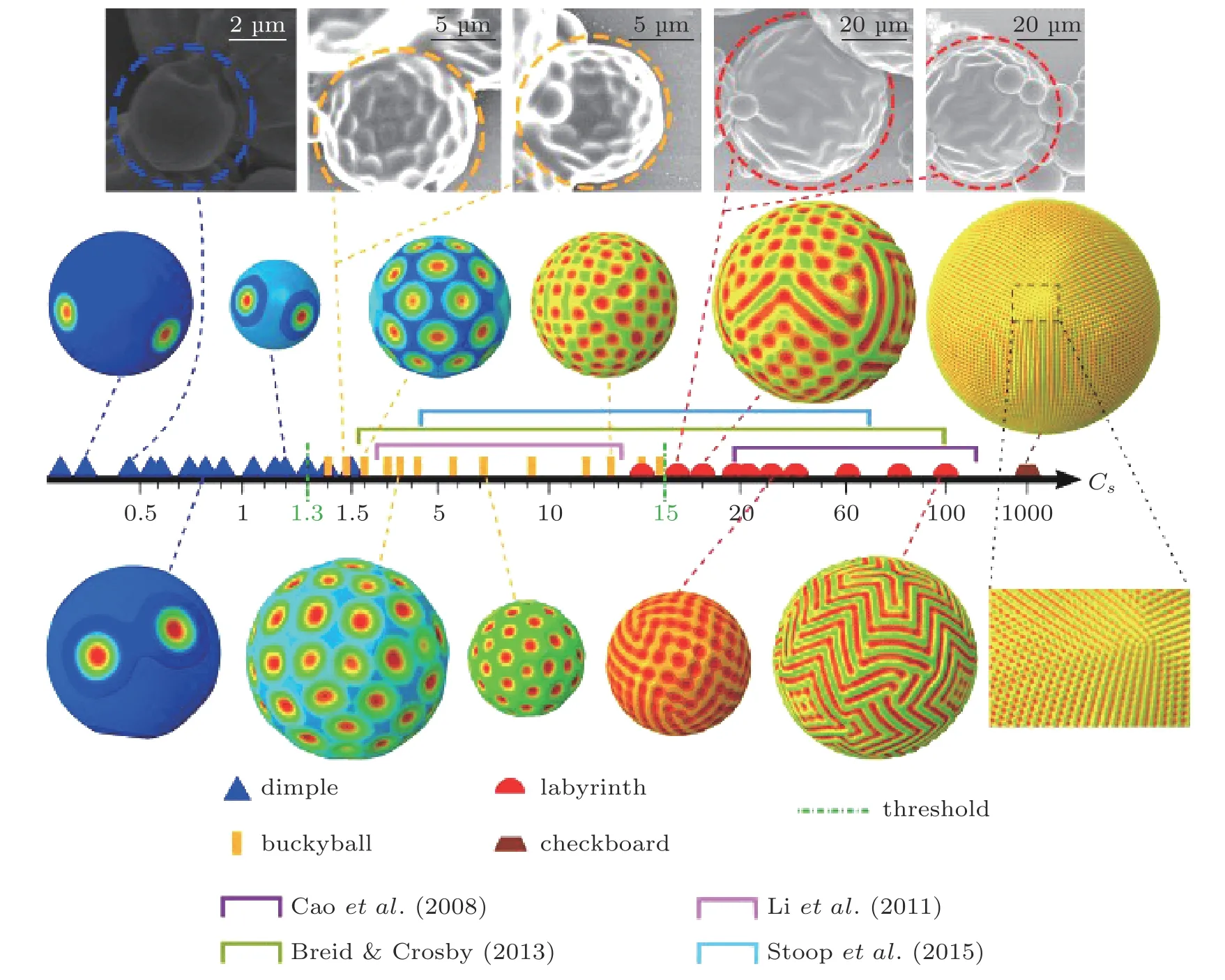
当柱面核壳结构受到轴向压缩时, 由于曲率与核心的共同作用, 薄壳可能先屈曲成轴对称的正弦形模态(见图6 (a)), 继续加载下转变成非轴对称的钻石形模态(见图6 (b)). 为表征柱面核壳结构的模态转化规律, Xu & Potier-Ferry (2016)通过分析基底与薄膜变形能量级, 得到一个无量纲参数

其表征了核壳弹模比Es/Ef和无量纲曲率半径R/hf. 当Cs≥0.9, 屈曲模态是轴对称的(见图6 (a)),且超临界分岔后的解是稳定的; 当Cs≤0.7, 柱面核壳结构发生亚临界二次分岔失稳成钻石形模态(见图6 (b)). 此外, 对于极软的核心, 其后屈曲行为接近于空心柱壳, 具有极强的缺陷敏感性.上述两种失稳形貌是轴压下柱面核壳结构的普遍形式, 除了在模态过渡区中(0.7 图6 外层壳和核心之间的失配应变可由外部激励引起的非均匀膨胀/收缩产生, 如热收缩(Tan et al.2019, Yuan et al. 2019), 溶剂引起的膨胀(Li et al. 2015, Yin et al. 2014)和体积增长(Ben Amar &Jia 2013). Chen & Yin (2010)在圆柱核壳结构中引入平面应变假设, 得到前屈曲中薄膜压应力为 式(27)表明,σ0受 基底曲率半径R、失配应变Δε和弹模比的影响. 从简化的环形平面应变膜基模型中可以得到临界波数nc、 临界波长λc、 临界应力σc、 临界应变εc和起皱幅值A(Chen & Yin 2010) 利用智能材料对多物理场激励产生的变形响应可用于形貌斑图的灵活设计与调控. Zhao等(2021)将液晶分子取向产生的各向异性自发应变引入经典DMV薄壳理论中, 发现当指向矢在圆柱面内排布时, 失稳形貌受核壳刚度比和曲率影响, 可出现轴对称、油条状或钻石模态; 当指向矢在圆柱面外分布时, 薄膜中的各向异性自发应变会导致斜条纹、平行珠链或钻石模态(见图7).通过改变液晶高聚物网络(LCN)薄膜中液晶初始指向矢方向, 可实现表面褶皱斑图的灵活设计. 图7 另一种典型情况是软壳在柱面核心上轴向受压无粘连滑移(见图8 (a)). 平面几何构型下在桌面上挤压一张纸的现象较为简单, 纸张整体屈曲成单一凸脊(见图8 (b)~图8(d)). Yang等(2018)发现柱面基底上软壳在轴向压缩下, 由于曲率的影响, 会首先屈曲成正弦形褶皱(见图8 (f)),实验与理论计算表明临界失稳应变与无核心圆柱壳轴向受压一致(van der Heijden, 2009) 图8 球面膜基是另一种常见的曲面复合结构, 具有正高斯曲率. 许多果实和蔬菜可看作具有核壳结构的球体或类球体, 其生长过程中呈现出多样的褶皱斑图形貌, 例如甜瓜、脱水花粉粒和青豆等(Yin et al. 2009, Yang et al. 2016, Li et al. 2011). Yin等(2009)基于弹性薄壳理论和有限元, 模拟分析了各种球形核壳结构的表面不稳定性和失稳模态. 他们发现球面核壳结构的失稳模态主要取决于有效尺寸/厚度比、赤道/极半径比和核壳弹性模量比. 考虑半径为R的球形基底, 覆盖一个厚度为hf的硬壳, 浅曲率球壳应变可表示为(Xu et al.2020b, Xu & Zhao 2020) 和柱面情况相比, 可以发现只在另一方向多了曲率影响, 即w/R. Li等(2011)通过临界稳定性分析和有限元模拟, 研究了neo-Hookean球面核壳结构因核心收缩引起的起皱和后屈曲模态. 当收缩达到临界值时, 球壳首先出现巴基球失稳形貌, 然后逐步演化为迷宫模态. 豌豆失水萎缩实验进一步验证了这一形貌的演化过程(见图9 (a)). 基于Koiter弹性壳理论, Stoop等(2015)发展了一种广义Swift-Hohenberg模型, 用于描述膜基结构褶皱形貌和模态选择. López-Jiménez等(2016)基于广义Swift-Hohenberg理论研究了曲率和拓扑结构对曲面核壳结构表面晶体压痕斑图的影响. 结果表明单个缺陷的位置和缺陷链的方向依赖于局部高斯曲率和梯度, 进一步说明曲率对膜基结构表面形貌演化有着重要影响. Zhao等(2020)进一步研究了曲率各向异性和曲率梯度对曲面膜基系统起皱的影响, 给出了描述各向异性曲率的模态选择相图. 他们发现, 当曲率张量为各向异性且褶皱垂直于主曲率时, 曲面膜基系统的初始不稳定模态是正弦形. 随着残余应力的增大, 正弦褶皱可演变为六边形, 并经历双稳态混合模态进一步转化为迷宫形貌. 图9 Xu等(2020b)从实验和理论上发现, 在核心收缩或表层膨胀时, 球面核壳结构的模态选择主要取决于单一的无量纲参数Cs(见图10). 当Cs<1.3时, 核壳结构通常经历亚临界分岔失稳成局部凹陷形貌; 当 1.3 图10 薄膜起皱现象由于其丰富的表面形貌和复杂的非线性力学行为, 过去二十年里引起了广泛的研究兴趣. 早期的工作聚焦于平面薄膜结构小变形起皱行为的临界分析, 近年的工作开始探究曲率对薄膜结构大变形失稳行为的影响, 促进了有限应变壳理论的发展. 研究发现增大初始曲率可抑制褶皱产生, 为薄膜结构平整化提供了新思路. 膜基双层结构中, 曲率不仅会改变薄膜起皱的临界载荷, 也会显著影响空间褶皱的模态选择和非线性演变, 具体可归纳为以下几点: (1)失稳的临界应变一般随曲率的增加而增加, 即曲率会延迟褶皱失稳; (2)曲率是调控表面失稳形貌的重要参数. 曲面核壳结构比平面膜基结构通常具有更大的变形, 更容易产生对称性破缺, 使其在不同几何曲率构型下产生更丰富多变的褶皱斑图; (3)曲面基底可以是实心的, 也可以是空心的,可具有各种各样跨尺度的几何构型. 虽然文献中已经实现了大量等曲率表面失稳形貌演化的模拟, 但对于非均匀曲率表面上更为复杂的起皱形貌的精确预测, 仍需要普适的理论模型和高效的计算方法. 理解曲率影响下薄膜结构的非线性失稳机理和形貌演化规律, 对于利用失稳实现多功能表面制造具有应用潜力, 可促进拓扑形貌相关的功能性薄膜结构的设计及优化. 致 谢国家自然科学基金(11872150, 11602058, 11772094); 上海市青年科技启明星计划(19QA 1400500)资助项目.
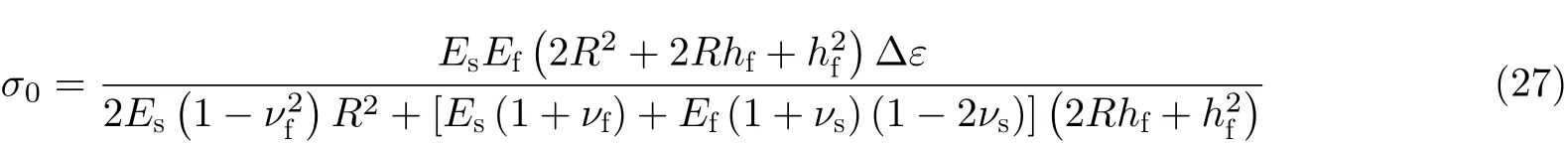
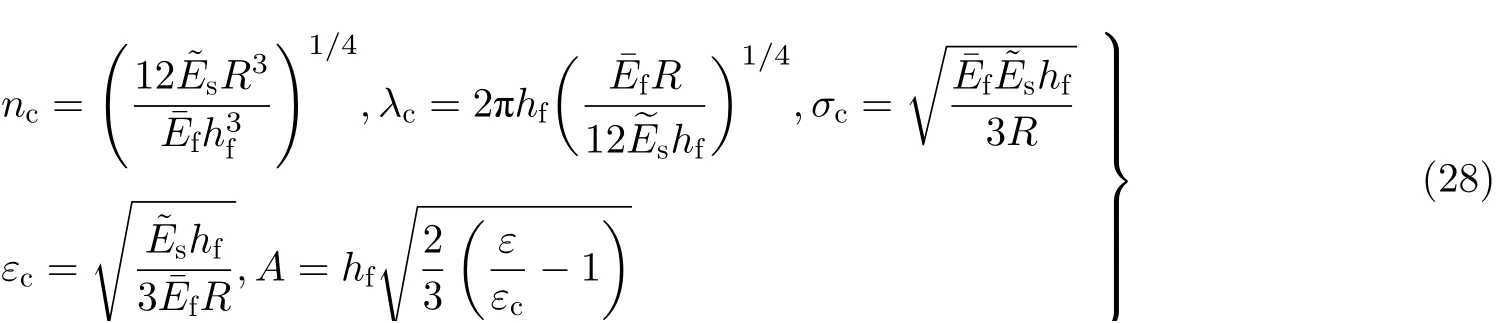
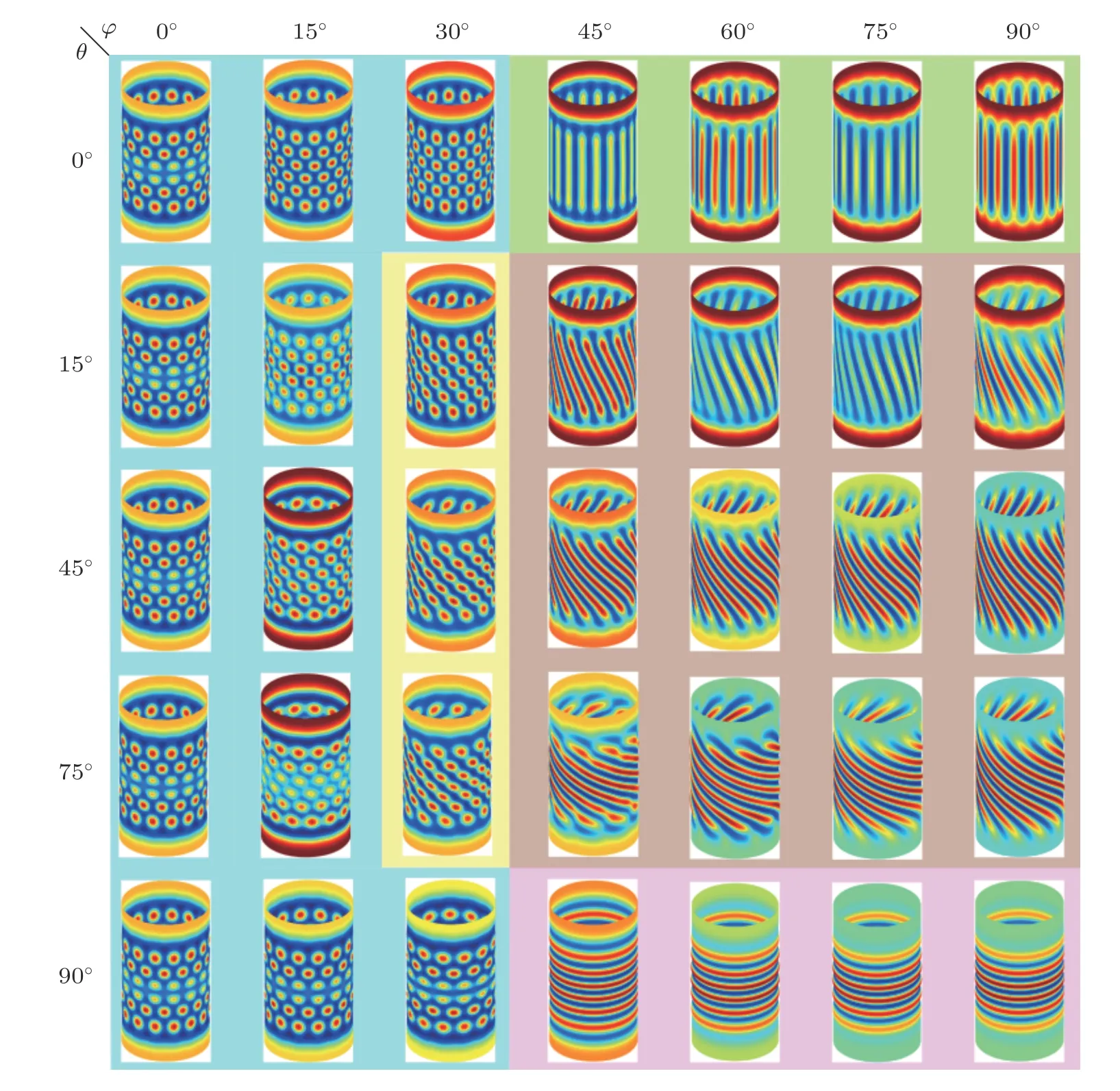


3.3 球面膜基结构


4 结论
