弹性拓扑材料研究进展
2021-11-17张亚飞夏百战刘晓宁周萧明陈常青胡更开
陈 毅 张 泉 张亚飞 夏百战 刘晓宁 周萧明 陈常青 胡更开 ,*
1 北京理工大学宇航学院, 飞行器动力学与控制教育部重点实验室, 北京 100081
2 清华大学工程力学系和微纳米力学中心, 北京 100084
3 湖南大学机械与运载工程学院, 汽车车身先进设计制造国家重点实验室, 长沙 410082
1 引 言
拓扑绝缘体(topological insulator)是近四十年来凝聚态物理领域备受关注的课题, 其单向传播、无损耗传输等新颖性质在波动控制方面极具应用潜力. 近十年, 拓扑绝缘体研究已拓展到经典电磁、声波、弹性波等领域, 为当前对经典波传播的调控与设计提供了新技术. 目前已有不少介绍拓扑绝缘体的论文, 但大多以电学或电磁学领域为主(Hasan et al. 2010, Qi et al. 2011,Asbóth et al. 2016, Ozawa et al. 2019), 不便于力学领域学者掌握拓扑绝缘体基本内容. 为此, 本文聚焦弹性波拓扑绝缘体研究, 特别从离散质量弹簧系统出发对拓扑绝缘体有关数学、物理概念进行详细解释, 并系统介绍当前研究最多的三类拓扑绝缘体(陈绝缘体、谷霍尔绝缘体、自旋霍尔绝缘体)的物理机制、刻画方法、波动规律与已取得的研究进展. 除引言中介绍拓扑绝缘体起源涉及到的物理背景以外, 文章其余部分均为动态、静态力学内容. 希望论文对打算开展拓扑绝缘体研究的力学工作者有所帮助.
本文介绍的拓扑材料主要指拓扑绝缘体, 为了涵盖文中也涉及到的静力学拓扑现象, 这里统一概括为广义的“拓扑材料” (topological material). 拓扑绝缘体概念与物理和数学都有着密切的联系(Hasan et al. 2010, Qi et al. 2011). 拓扑(topology)一词来自于数学中的拓扑学分支(Willard 2012), 与几何体或抽象的数学对象在光滑连续变化时仍保持不变的特性相关. 拓扑学即是研究这些不变性质的一门重要数学分支. 比如, 球形橡皮泥和圆饼状橡皮泥在几何上是拓扑等价的,它们均包含0个孔洞, 在不将橡皮泥撕裂的前提下, 通过挤压可使橡皮泥形状在两者之间相互转换(图1). 实际上, 中间形态也与球体拓扑等价. 如果在挤压过程将橡皮泥撕裂产生新的孔洞, 则几何拓扑发生改变. 例如, 产生1个孔洞得到的几何体与甜甜圈形状等价.
如何对拓扑进行定量描述正是拓扑学研究的内容. 比如, 上述几何体孔洞数就可根据微分几何中的高斯伯内特定理(Gauss-Bonnet theorem)严格地计算得出

其中,K代表局部高斯曲率, ∂Ω为几何体边界,X就是几何体的拓扑数或拓扑不变量(topological number, or topological invariant). 对任意光滑几何体, 以上公式的取值均为精确整数. 正因为这一点, 当几何体在光滑连续变化时, 其拓扑数不会改变, 仅当几何体出现撕裂等不连续变化情况时,拓扑数才会发生突变. 这一积分公式取值不随几何体连续变化而改变, 与常规积分公式存在显著差别, 比如体积则随几何体变化而连续地变化.
拓扑绝缘体得名“拓扑”二字的主要原因在于其拓扑特性. 拓扑绝缘体内部不导电, 但在其边界则可以导电, 且这种导电特性是一种拓扑特性, 即材料或系统参数光滑连续变化时不受影响(图1 (b)). 与之相对的普通绝缘体在内部和边界上均不能导电, 且容易受到杂质、缺陷等影响.
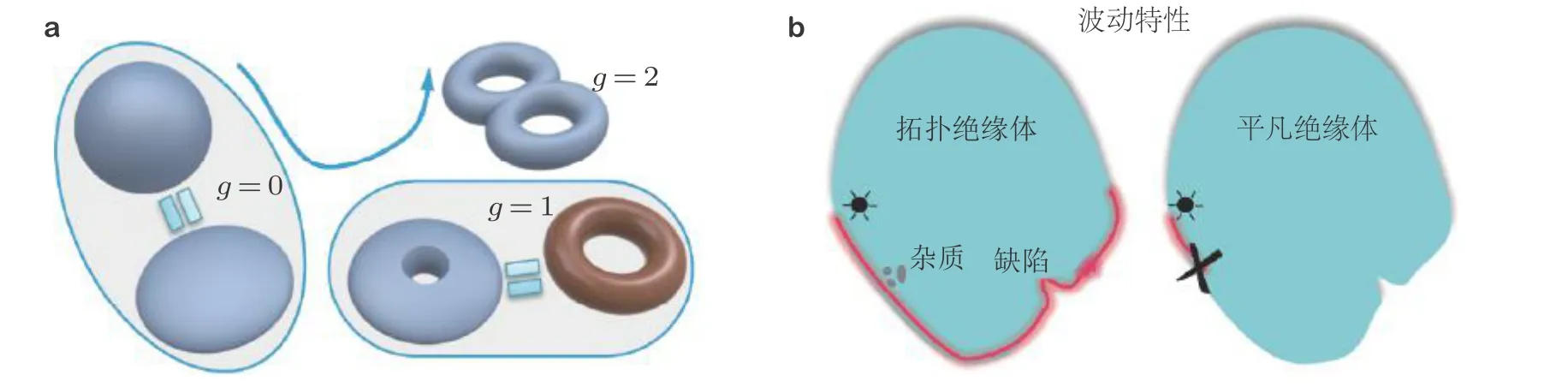
图1
拓扑绝缘体的发现可追溯到20世纪80年代, 德国物理学家von Klitzing等(1980)测量了二维电子材料在外磁场作用时的边界导电性, 发现材料的电导为基本量e2/h的精确整数倍,σ=nHe2/h, 偏差小于十亿分之一. 此外, 电导随外磁场强度的增加呈现台阶状突变, 即呈现精确量子化现象, 并且对边界缺陷等参数变化不敏感, 这就是经典的“整数量子霍尔效应”(integer quantum Hall effect) (Cage et al. 2012). 因发现这一奇特物理现象, von Klitzing获得了1985年诺贝尔物理学奖.
为了解释整数量子霍尔效应的物理机制, 研究者从不同角度进行了阐释(Laughlin 1981,Thouless et al. 1982, Haldane 1988, Hatsugai 1993). 从其物理表现形式不难得出, 整数量子霍尔效应与拓扑之间应该有着密切的联系. Thouless等(1982)给出了与拓扑最接近的解释. 他们从理论上揭示了电导与系统体态之间的关系, 并给出了计算导电特性的数学公式

式中i为能带编号,ui(k,r)为第i支能带上波矢k对应的布洛赫模态(Bloch mode),u¯i(k,r)为该布洛赫模态的复共轭, 求和符号针对费米能级以下所有能带,nH表达式中关于dk2的积分区域为第一布里渊区(first Brillouin zone). 可以证明,nH是一个精确的整数, 后被称为TKNN数, 是反映系统是否具有量子霍尔效应的拓扑数. 以上积分公式与拓扑学中的第一陈示性类(first Chern class)相关(Qi et al. 2008), 由我国著名数学家陈省身提出. 所以, 后来TKNN数又被称为陈数(Chern number) (Hatsugai 1993). 如果绝缘体的陈数为零, 则称为普通绝缘体, 否则称为拓扑绝缘体, 或更具体地称为陈绝缘体(Chern insulator). 式(2)与计算几何孔洞的式(1)有如下相似与不同之处. 第一, 由于倒格空间(reciprocal space)中布里渊区的周期性, 式(2)中的积分区域等价于封闭圆环曲面(图2). 第二, 这里研究对象不是二维圆环曲面本身, 而是曲面上的布洛赫模态场,是一种更抽象的数学对象. 最后, 被积分对象称为贝里曲率(Berry curvature), 是刻画曲面上布洛赫模态内在性质的物理量.
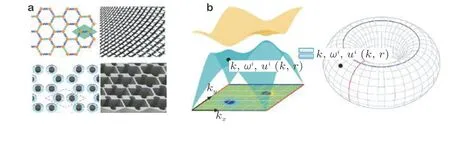
图2
需要说明的是, 上述拓扑数只取决于材料的体态性质, 而量子霍尔效应却是材料的边界特性.这是拓扑绝缘体的一个独特地方, 其体态性质可以决定边界的导电性质, 即拓扑绝缘体研究领域著名的体边对应关系(Bulk-edge correspondence) (Hasan et al. 2010, Qi et al. 2011): 在陈数不相等的两个绝缘体的公共界面, 存在与拓扑数之差相等数目的拓扑界面态, 电子波可以不受干扰地绕过缺陷、杂质向前传播. 这种拓扑性质可以从物理上大致理解为, 由于磁场打破了系统的时间反演对称性, 电子只能沿单向传输, 因此其即使遇到缺陷或杂质也无法产生后向散射, 只能继续向前传播. 只有外磁场方向反转时, 允许的拓扑态方向才相应发生反转.
量子霍尔效应需要外部强磁场打破系统的时间反演对称性, 但强磁场不利于实际应用. 美国物理学家Haldane (1988)提出了一个仅包含内部磁链的二维模型, 该模型也打破时间反演对称性, 可以实现量子霍尔效应. 这导致在很长一段时间内, 研究者都认为, 时间反演对称性破缺是实现拓扑现象所必须的. 直到2005年左右, 量子自旋霍尔效应(quantum spin Hall effect)的提出打破了传统认知(Kane et al. 2005a, Hasan et al. 2010). 在量子自旋霍尔效应中, 电子的内在自旋特性起到了类磁场作用, 上自旋电子和下自旋电子沿着界面相反的方向传输, 且其电导特性一样呈现精确量子化现象. 之后, 还发现了量子谷霍尔效应(quantum valley Hall effect), 既不需要打破时间反演对称性也不依赖电子自旋(Tworzyd et al. 2007, Xiao et al. 2007). 这三类拓扑波动现象是目前二维体系中研究最广泛的, 分别对应霍尔绝缘体(Hall insulator or Chern insulator)、自旋霍尔绝缘体(spin Hall insulator)和谷霍尔绝缘体(valley Hall insulator).
尽管拓扑绝缘体最早在量子波领域中发现, 但其拓扑本质主要与波动行为相关, 而量子特性并不是其必备条件. 从式(2)可以看出, 这种拓扑特性来源于电子布洛赫模态的内在特性. 实际上, 经典波动领域的周期介质, 如光子晶体、声子晶体等, 也有相对应的布洛赫波模态. 因此, 拓扑绝缘体概念可以自然地拓展到经典波领域. 近十年来, 电磁波、声波拓扑绝缘体得到了快速的发展(Tworzyd et al. 2007, Xiao et al. 2007). 对应的弹性波领域有关进展则相对较少, 这与弹性波本身及弹性波理论更复杂有关. 例如, 声波只有纵波模式, 电磁波只有横波模式, 而弹性波则通常耦合有横波与纵波(Achenbach 2012). 不过复杂性中也蕴含着新的机会, 例如, 弹性体表面的瑞利波就有类似的赝自旋效应(pseudo spin) (Long et al. 2018), 或许可以更简便地设计类自旋霍尔绝缘体. 此外, 弹性波研究中梁、薄板等各种波导(Vila et al. 2017; Yan et al. 2018; Miniaci et al.2018; Zhang et al. 2019a, 2020; Gao et al. 2021)也提供了丰富的拓扑绝缘体实验研究平台. 将量子中的拓扑现象拓展到经典波领域, 一方面可以拓展经典波动调控设计能力, 如实现单向传播、缺陷免疫波导等新颖功能. 同时, 也为探索量子拓扑现象提供了新的平台, 经典波现象属于宏观领域, 无论在观测技术或是操控手段方面都比微观量子领域更加容易.
本文主体框架以作者所在各课题组开展的相关研究为基础, 着重介绍谷霍尔绝缘体、陈绝缘体与自旋霍尔绝缘体设计机理、理论刻画方法, 并概括有关实验验证. 为方便读者了解更全面的拓扑研究内容, 本文还简单介绍了近期研究较多的高阶拓扑现象、静力学中的拓扑现象. 论文内容安排如下: 第二节从一维、二维质量弹簧系统出发, 对拓扑研究相关概念进行了详细阐释,包括狄拉克锥、确定性简并、能带翻转、贝里曲率、拓扑不变量等基本概念, 重点是周期离散系统的k∙p微扰等效模型建立方法, 及该等效方法在计算拓扑数和解析求解拓扑界面态中的应用. 第三至第五节为本文主要内容, 依次为谷霍尔绝缘体、陈绝缘体及自旋霍尔绝缘体研究进展. 第六节简要介绍角态高阶拓扑绝缘体概念与基本设计思路, 第七节为多稳态系统中出现的拓扑孤立子、Maxwell桁架中的拓扑零能模式这类静态拓扑现象. 文末是总结与展望.
2 拓扑绝缘体基础
2.1 一维质量弹簧链系统
本小节以一维质量弹簧链系统为例, 介绍一维拓扑相关概念. 考虑如图3 (a)所示的双原子链模型(Chen et al. 2018a), 其晶格常数记为a, 单胞内包含两个质量块m1和m2, 两个弹簧刚度分别为k1和k2. 记第n个单胞内的第j(j= 1, 2)个质量块的位移为并假设m1=m2=m, 系统的运动方程可表示为

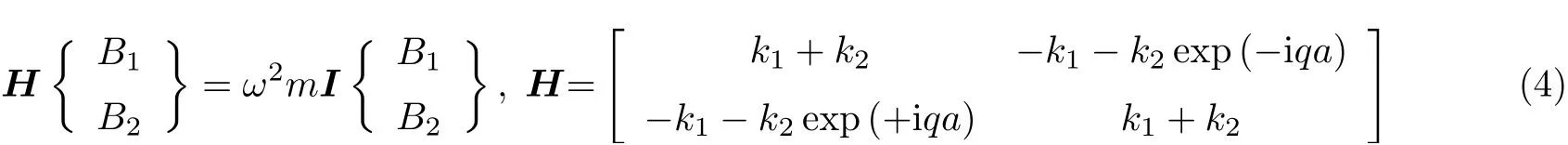
该特征值方程刻画了系统的频散特性.图3 (b)给出了三种典型情况的频散曲线, 分别对应γ= 0.2,γ= 0和γ= −0.2. 其中,γ= (k1−k2)/(k1+k2), 无量纲化频率
如图3 (b)所示, 从频散曲线上看, 构型γ=γ0和γ= −γ0(γ0≠ 0)并无任何区别, 但两者的拓扑性质完全不同, 这反映在相应的特征模态上. 当γ的值由正变负时,q= π/a处的特征模态发生翻转. 如图3 (b)中插图所示, 构型γ= 0.2的声学频散分支的特征模态与构型γ= −0.2的光学频散分支相同, 而构型γ= 0.2的光学频散分支的特征模态与构型γ= −0.2的声学频散分支相同. 这种能带翻转现象不是偶然发生的, 其必须通过带隙关闭(γ= 0)进行过渡. 下面将借助拓扑语言说明,若不经过带隙关闭, 无论怎么调节k1与k2, 均不会发生上述能带翻转现象.

图3
为此, 接下来研究声学频散分支的拓扑性质, 计算波数由q= − π/a变为q= π/a过程中声学分支特征模态的相位积累θ. 一般地, 对于两个模为1的复数z1= exp (iβ1)和z2= exp (iβ2), 其相带翻转位差为这里要求δz=z2-z1≈ 0. 则波数从q= − π/a变为q= π/a时积累的相位差为

其中〈,〉表 示厄米点积,φ(q)为声学分支波数q对应的归一化特征模态k2exp(iqa). 将归一化特征模态φ代入式(5), 可得

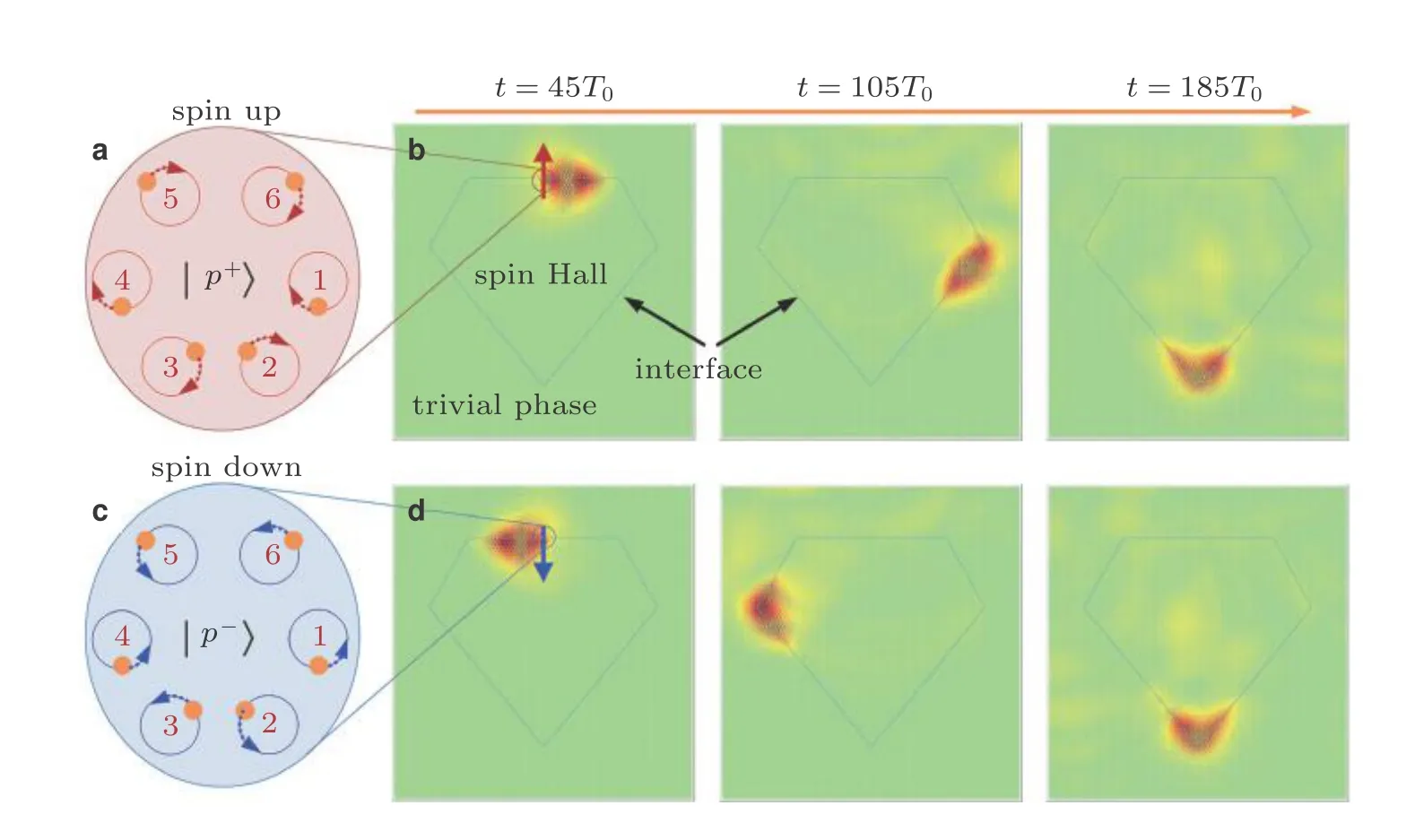
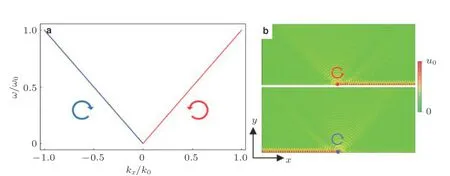
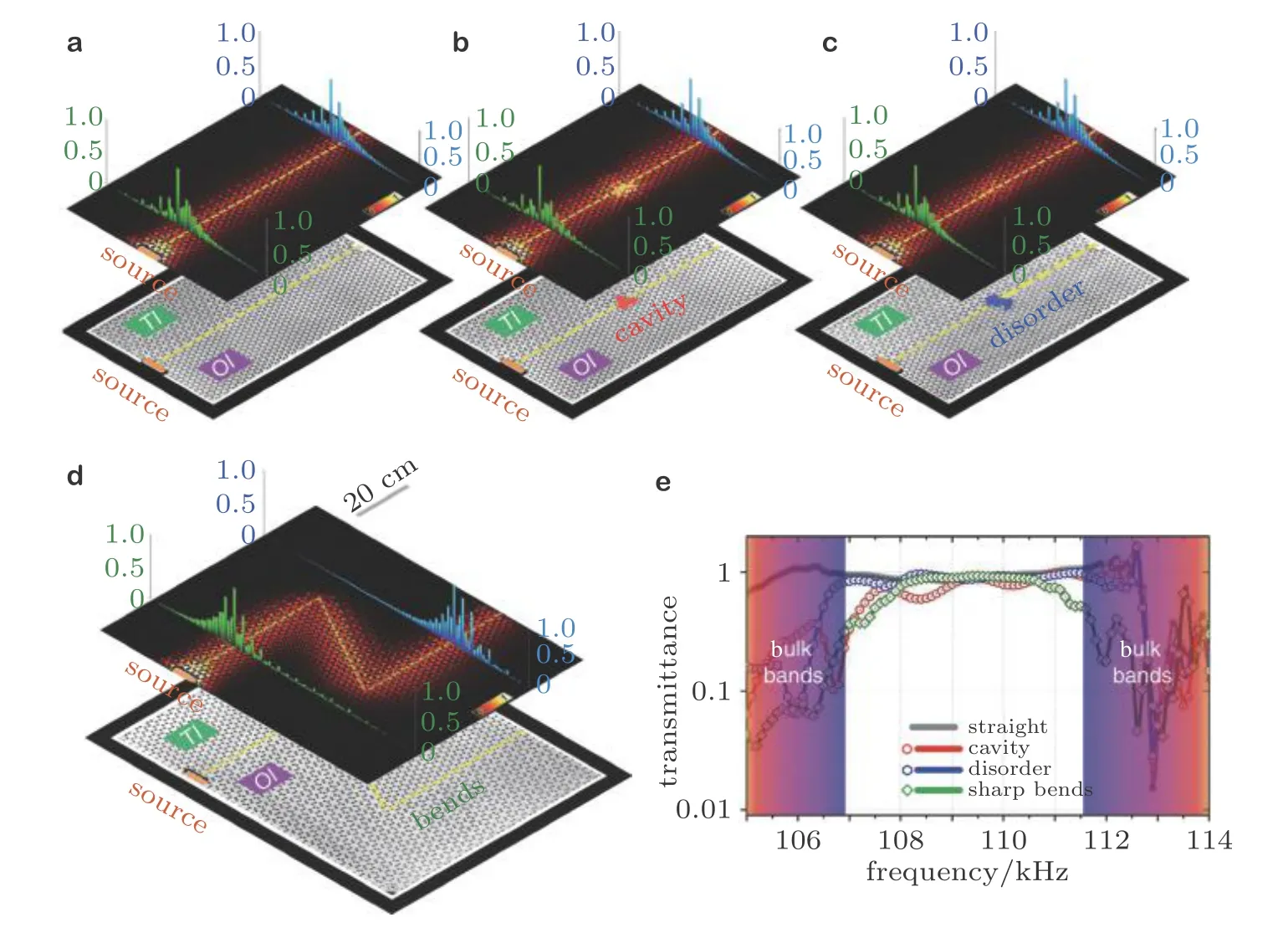
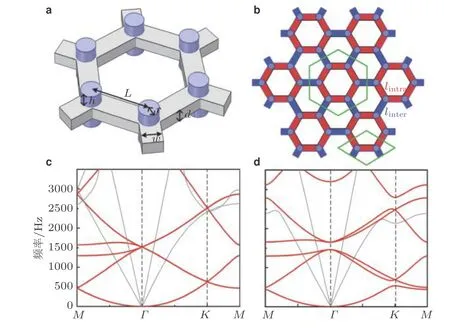
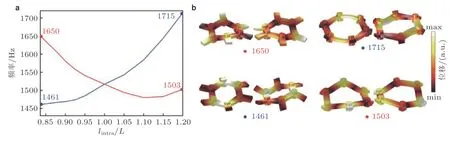
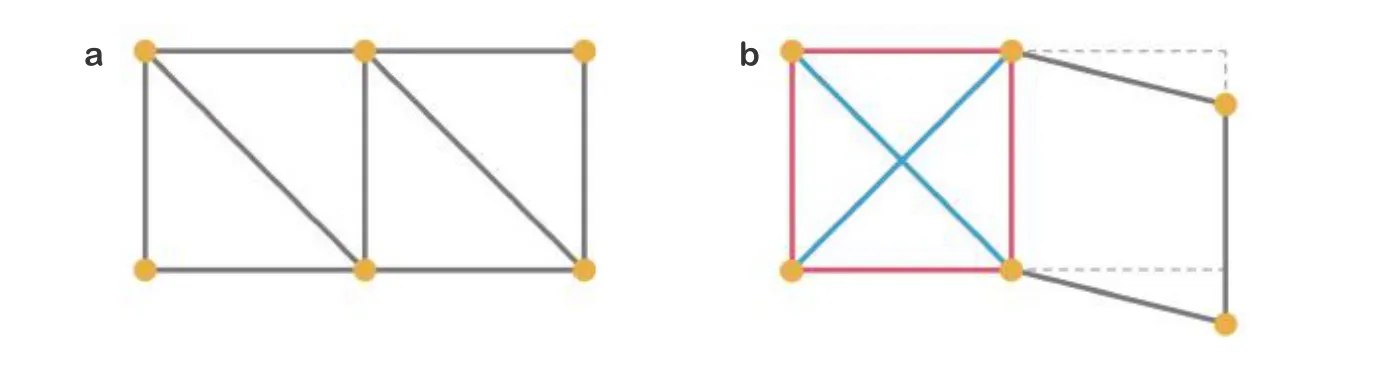
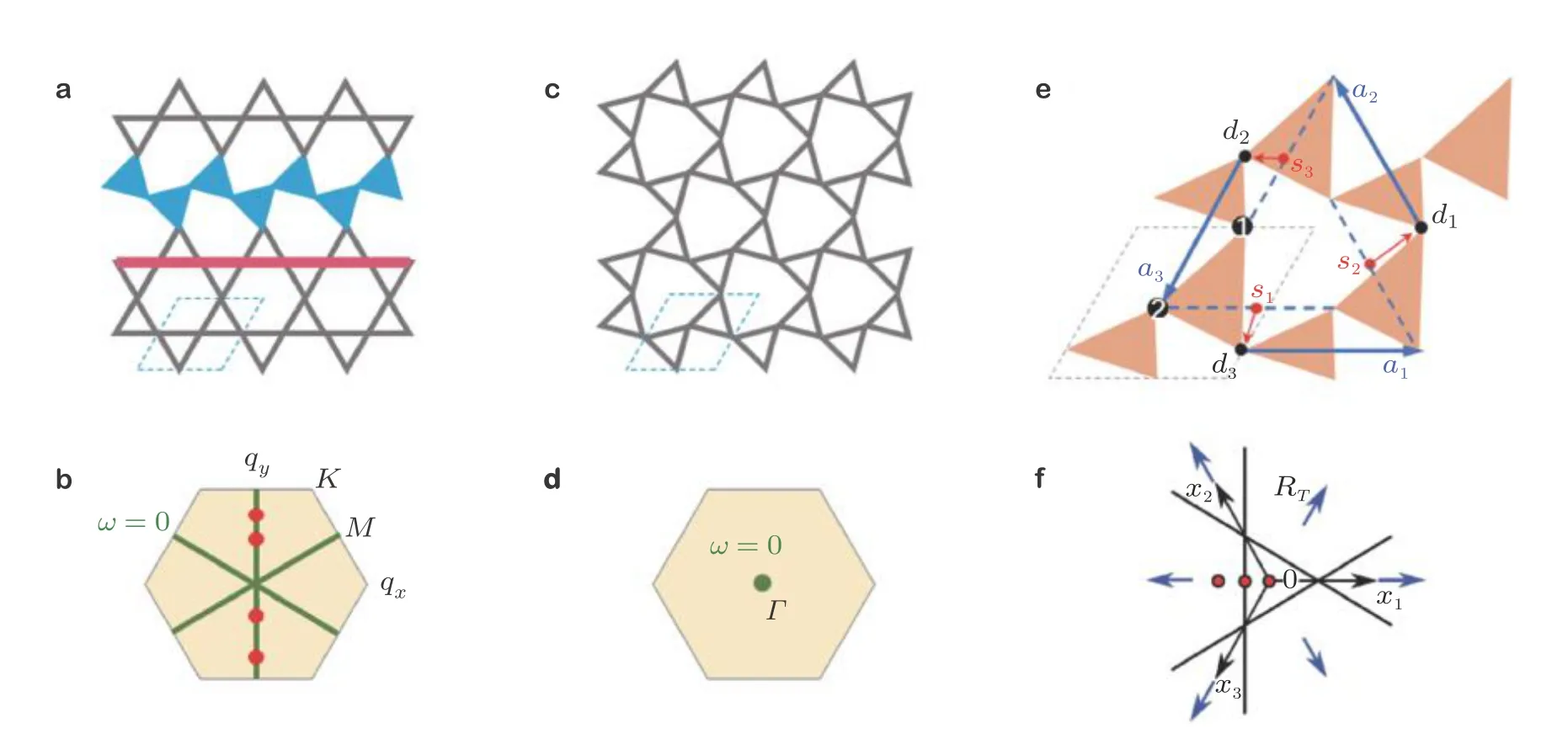
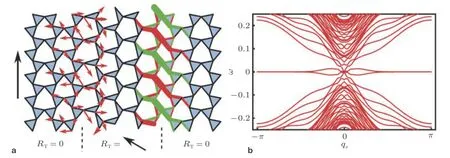
θ就是所谓的Zak相位(Zak 1989), 类似于后续小节即将介绍的贝里相位(Simon 1983). 两者均用于描述系统的拓扑属性, 区别在于Zak相位特别针对一维材料, 而贝里相位用于二维或三维材料. 另外一个关于一维材料的拓扑不变量是缠绕数υ(Ryu et al. 2010), 其与Zak相位的对应关系为υ=θ/π. 由此可见, 能带翻转意味着θ由0变为π, 也就是υ由0变为1. 为了更生动地说明这一点, 将z(q)表示的封闭曲线η绘制在复平面上, 如图4所示. 当k1>k2时, 复平面原点不被包含在封闭曲线η内部, 对应于υ= 0. 当k1 图4 上述分析表明, 构型k1>k2和k1 图5 进一步考虑两侧各有200个单胞的含界面点阵结构(图6 (a)), 界面两侧的单胞中,k1与k2发生了交换. 由于界面两侧材料的缠绕数绝对差值为1, 无论γ为正或负, 材料体带隙范围内均存在1支界面态模式(图6 (d)).图6 (b)(c)分别给出了γ= −0.5和γ= 0.5时的界面模态. 可以看到, 两者对应的位移分布还是有明显区别的. 当γ< 0时, 界面处的质量静止且位移分布关于界面反对称. 而当γ> 0时, 界面处的质量具有最大的振荡幅度且位移分布关于界面对称. 类似的现象也出现在二维拓扑系统中, 将在后续章节中介绍. 图6 本小节以二维蜂窝质量弹簧系统为例(Chen et al. 2019), 说明二维拓扑绝缘体研究有关概念.二维周期蜂窝点阵系统如图7 (a)所示, 高亮六边形区域为一个单胞, 单胞内包含两个质量点, 记作p和q, 其质量分别为mp和mq, 最近邻质点由刚度为t的弹簧连接. 为简化表达, 设弹簧长度及刚度分别为L0= 1 m和t= 1N/m. 长度为的两个晶格矢量为a1= (ax, −ay) = (3L0/2,根据晶格矢量可将每一个六边形单胞用两个数字进行编号(m,n),m和n取值为0, −1, +1, −2, +2, ···. 计高亮区域单胞编号为(0, 0), 编号为(m,n)的单胞, 可由编号为(0, 0)的单胞沿矢量ma1+na2平移得到.图7 (b)给出了蜂窝系统的第一布里渊区, 两个倒格矢量为倒格矢量与晶格矢量之间满足关系ai∙bj=δij,δij代表克罗内克尔符号. 图7 考虑面内弹性波在该点阵中的传播. 由于系统的周期特性, 可假定其波动解为布洛赫形式,即位置矢量相差ma1+na2的质点的位移解仅存在相位差exp [−ik·(ma1+na2)],m和n为整数,为布洛赫波矢. 位移解可具体表示为其中,为 编号(m,n)的胞元中p质点的位移矢量,为胞元(0,0)中p质点的位移矢量, 不同胞元内q质点的位移满足相似关系. 根据布洛赫波特征, 只需要对单胞进行分析, 即可得出整个结构的波传播规律. 具体以编号(0, 0)的胞元为例, 分析其p和q两质点的平衡方程. 考虑小幅简谐振动问题, 频率记为ω, 质点p和q各受到三个相邻质点施加的弹性力, 其平衡方程为 其中,ex= (1, 0),et= (cos(2π/3), sin(2π/3)),et′ = (cos(−2π/3), sin(−2π/3))为三个沿弹簧方向的单位矢量. 将布洛赫解形式代入上式, 可以得到如下矩阵表示的特征值方程 U为p和q两个质点的位移组成的特征向量U= {up,uq}. 质量矩阵M4×4和刚度矩阵K4×4(k)分别为 符号†代表复共轭转置.I为2 × 2的单位矩阵. 方程(9)的解即为点阵中允许的布洛赫模态. 为了得到非平凡的零解, 系数矩阵的行列式必须为零Det(ω2M4×4+K4×4(k)) = 0, 据此可求解出色散关系ω(k), 以及对应的模态. 简单计算后, 得到上述4 × 4矩阵特征值的4个解, 其色散关系分别为 其中Y= 2[8cos(kxax)cos(kyay) + 4cos(2kyay) − 3]/9. 特征模态的表达式比较繁琐, 这里就不再详细给出. 第1和第4阶色散关系与系统剪切波模态对应, 其取值为常数, 这里重点关注第2、第3支色散曲线. 第2、第3阶色散曲线在布里渊区角点K和K′处达到极值ω= (3t/2mp)1/2, (3t/2mq)1/2,此处局部特征频率呈现山谷顶或谷底形式, 因此, 波矢K和K′又被称为谷(valley), 对应的特征模态被称之为谷态(valley state). 在谷点K′处, 与特征频率ω= (3t/2mp)1/2和(3t/2mq)1/2对应的特征模态分别为 由于系统满足时间反演对称性,K对应谷态为上述谷态的复共轭形式 对于u1(K)/u1(K′)谷态, 胞元内质点p在x和y方向的位移大小相等, 相位相差π/2, 代表质点p绕平衡位置作顺/逆时针圆周运动, 而质点q静止不动. 对于u2(K)/u2(K′)谷态, 质点q绕平衡位置作逆/顺时针圆周运动, 而质点p则静止不动. 图8 给出了单胞中两个质点的质量相等(mp=mq= 1.0,t= 1.0)及不等(mp= 0.9,mq= 1.1,t=1.0)两种情况下的色散曲面. 可以清晰地看出, 第2、第3支色散曲面在布里渊区角点K′和K处取极大、极小值. 当两个质点的质量相等时(图8(a)), 色散曲面在K′和K处取得相同频率, 称为简并频率. 简并频率附近色散曲线与波矢线性相关Δω~ Δ|k|, 即局部色散曲面在K′和K呈现为双圆锥, 被称为狄拉克锥. 反之p和q质量不等时(图8(b)), 系统的对称性降低, 第2、第3支色散曲面在K′和K取值不等, 简并被破坏. 第2支色散曲面的极大值频率与第3支色散曲面的极小值间的频率范围称为系统的禁带, 系统不能传播频率处于禁带的波. 图8 上述简并由系统的对称性决定, 被称为确定性简并(deterministic degenerate), 当相应的对称性被破坏后, 对应的简并状态也会被打破. 针对上述蜂窝点阵质量弹簧系统, 当p和q质点相等时, 系统满足C6v对称性. 其中, C对应英文名称为Cyclic, 代表旋转对称性, 与数字n组合一起表示系统每旋转360o/n不变, 而v表示系统还具有与旋转轴平行的镜像对称面. 除了结构本身的对称性之外, 波矢位置的对称性也很重要. 针对上述系统,K′点和K点满足C3v对称性, 则系统在K′和K存在某两支色散曲面简并的情况, 具体是哪两支则视特定系统而定. 对于确定性简并, 只要需求的对称性不被破坏, 则简并始终存在. 例如对于上述蜂窝系统,p和q质量同时增大或减小仅改变简并频率, 不改变第2、第3支色散曲面在K′和K的简并特征. 除对称性带来的确定性简并, 特定的参数组合也可使系统产生简并, 称为偶发简并. 根据文献中的研究(Lu et al. 2014), 将可能的几种简并类型总结如表1, 读者可以参考文献了解证明细节. 表 1 二维对称系统中狄拉克简并情况总结 2.2.1 k ∙p微扰等效模型 k∙p微扰等效模型(Lu et al. 2014)是研究参数扰动对系统波动规律影响的有效方法, 可以将离散系统的波动描述连续化, 便于从解析角度分析系统的拓扑特征. 这里以蜂窝质量弹簧点阵为例子, 说明如何推导得出系统的微扰等效模型. 在系统p和q质点质量相等时mp=mq, 第2、第3支色散曲面将在K和K′发生简并, 其对应的特征模态由式(13)(14)给出. 下面考虑p和q质量不相等mp≠mq的情况, 则系统对于任意波矢k的布洛赫解u′(k)满足与方程(9)一样的形式 进一步假定参数满足|mp−mq| << 1, 则该系统可认为是由p和q质量均为(mp+mq)/2的系统微扰而来, 后者在K(K′)简并, 其第2、第3阶特征模态由式(13)(14)给出. 因此, 微扰后的系统在K(K′)附近波矢的第2、第3阶特征模态可由微扰前系统的特征模态的线性组合近似得到, 以K′附近波矢k=K′ + Δk为例 将上述表达式代入其严格的波动方程(15), 并分别与u1(K′)和u2(K′)内积可以得到两个线性方程 将简并系统特征模态代入, 并化简可得到关于系数c1和c2的线性方程组 将上式截取到关于Δk的一阶近似项 上述方程中, ΔH代表系统的等效哈密顿量,ψ= {c1,c2}T为由线性叠加系数组成的特征模态. 参数τ= +1 (−1)用于区分K′(K)谷点,σx,σy和σz称为泡利矩阵(Shen 2017). 参数m和v表示系统的等效狄拉克质量(Dirac mass)和狄拉克速度(Dirac velocity). 根据以上等效模型, 可以得到Δω关于Δk的表达式及相应的特征模态 这里, 特征模态ψ满足归一化条件〈ψ|ψ〉=ψ†ψ= 1. 结合谷点波矢K′(K) 和已经确定的狄拉克锥点频率ω0, 可以得到谷点波矢K′(K) 附近的真实色散关系, 表示为K′(K) + Δk与ω0+ Δω的关系. 可以看到, 上下两阶色散曲面关于Δω= 0对称, 两阶色散曲线之间禁带宽度为|2m|. 当p、q质量相等的时候, 禁带消失, 两阶色散曲线在Δk= 0处形成斜率为v的狄拉克锥. 引言部分已提到, 目前研究较多的二维拓扑绝缘体有三类: 陈绝缘体、自旋霍尔绝缘体及谷霍尔绝缘体. 上述三类拓扑绝缘体分别由陈数、自旋陈数以及谷陈数拓扑数刻画, 拓扑数为零对应平凡绝缘体, 否则为拓扑绝缘体. 下面概括三类拓扑绝缘体的基本特点和波传播规律, 拓扑数的计算在后文具体加以说明. 霍尔绝缘体对应于最早发现的整数量子霍尔效应(Klitzing et al. 1980), 其边界支持单向传播态, 这对于能量单向传输极具意义. 实现霍尔绝缘体的关键在于打破时间反演对称性(Bansil et al.2016, Qi et al. 2011, Hasan et al. 2010), 如何在弹性波中做到这一点是设计的主要难点. 目前主要有两种思路, 一是将弹性波系统与旋转陀螺相耦合(Wang et al. 2015a, Suesstrunk et al. 2015,Nash et al. 2015, Zhao et al. 2020), 利用陀螺自身的旋转打破时间反演对称性; 另一种是利用科里奥利力打破时间反演对称性, 如将系统放置于非惯性系旋转平台(Wang et al. 2015b, Chen et al.2019). 无论是利用陀螺力或是科氏力, 当前的研究主要偏向于理论设计或者是基于离散模型的验证, 在连续的弹性体上开展的实验研究还未有报道. 根据体边对应关系(Wang et al. 2015b,Chen et al. 2019), 陈绝缘体与平凡绝缘体组成的界面支持拓扑保护的单向界面态, 即在材料界面发生弯曲或者材料有缺陷时, 能量都只能往前传播不会发生后向散射, 称为后向散射免疫(backscattering immune). 典型的陈绝缘体界面带结构如图9 (a)所示, 在禁带范围内仅有单向传播的边界态. 这里说明一下, 真空可以看作平凡绝缘体, 因此, 陈绝缘体的边界本身也支持以上单向态. 陈绝缘体的单向态在能量无损传输方面具有潜力, 但物理上通常难以打破时间反演对称性.随着研究的深入, 后来发现了自旋霍尔绝缘体这类特殊绝缘体, 其对应的拓扑数为自旋陈数(Kane et al. 2005a, 2005b; Bernevig et al. 2006). 事实上, 拓扑绝缘体最早就特指自旋霍尔绝缘体,后来才逐渐涵盖更广义的陈绝缘体、谷霍尔绝缘体等. 自旋霍尔绝缘体不需要打破时间反演对称性(Kane et al. 2005a, 2005b; Bernevig et al. 2006), 在其界面上存在传播方向相反的界面态, 分别对应于上、下两种自旋, 典型界面带结构如图9 (b)所示. 通过选择性地激发上或下自旋, 可以实现能量传播方向的控制, 由于无需打破时间反演对称性, 因此更利于实际应用. 只要缺陷不是特别强, 不使得自旋或者赝自旋自由度翻转, 就能保持对缺陷的鲁棒性. 由于弹性波不存在类似电子的内秉自旋, 要在弹性波中实现自旋霍尔绝缘体, 需要特别构造赝自旋态. 现有的设计包括:利用薄板结构的对称反对称模态耦合(Mousavi et al. 2015, Miniaci et al. 2018), 或基于超胞晶格布洛赫模态的构造方案(Yu et al. 2018, Li et al. 2018). 实际上, 弹性波天然包含复杂的耦合特性,例如, 弹性体表面的瑞利波就有类似的自旋效应(Long et al. 2018), 目前还没有这种类自旋特性的霍尔绝缘体设计. 图9 谷霍尔绝缘体是实现条件最简单的一类, 目前的研究也非常多(Lu et al. 2016, Xiao et al.2007, Vila et al. 2017, Pal et al. 2017, Xia et al. 2018, Zhang et al. 2019a, Chen et al. 2019, Gao et al.2021). 一般来说, 谷霍尔绝缘体可通过简单地打破狄拉克锥简并来实现, 如打破反演对称或镜面对称等空间对称性. 谷霍尔绝缘体一般在两个谷点附近的贝里曲率相反, 因此, 贝里曲率在整个布里渊区的积分等于零. 但是, 贝里曲率在谷点附近的积分等于半整数, 可分为正、负两种谷霍尔绝缘体. 在正、负两种谷霍尔绝缘体组成的界面上, 存在沿双向传播的界面态, 典型界面带结构如图9(c)所示. 尽管正负谷霍尔相组成的界面不具备单向导波特性, 但其波动的拓扑特征得到了很好的保留, 同样具有对缺陷、扰动不敏感的特征. 下面将按照设计难易程度顺序对弹性波谷霍尔绝缘体、陈绝缘体及自旋霍尔绝缘体的研究进展进行介绍, 并重点以前一小节提出的蜂窝质量弹簧系统为例, 对拓扑绝缘体设计、分析与计算中用到的理论方法进行详细介绍. 这里将介绍在2.2小节所述蜂窝质量弹簧系统中实现谷霍尔绝缘体. 实现谷霍尔绝缘体一般需要打破镜像对称或空间反演对称. 当上述蜂窝单胞中两个质点质量不相等时, 系统不再满足空间反演对称性, 先前的理论分析也表明, 系统原本满足的狄拉克简并破缺并产生完全禁带. 此时系统是否属于谷霍尔绝缘体可以通过计算谷陈数加以判断. 之前导出的微扰等效模型对于理论分析系统的拓扑不变量十分方便, 并且在后续拓扑界面态的解析求解中也非常实用. 拓扑数可由贝里曲率经过积分得到, 贝里曲率定义类似式(2) 根据微扰等效模型给出的特征模态式(23), 可以解析求出低频色散曲面分支的贝里曲率为 与先前类似,τ= −1或+1分别对应于两个谷点. 当然, 精确的贝里曲率也可以根据严格的特征问题方程式(9)的特征模态求出.图10 (a)中给出了精确带结构曲线以及在谷点附近的解析色散曲线, 而贝里曲率解析结果式(25)与精确结果对比如图10 (b)和图10 (c)所示. 其中解析结果与精确结果吻合很好, 印证了k∙p微扰等效模型的有效性. 注意到贝里曲率精确模型与解析模型之间的细微差别, 精确结果具有和系统类似的120°旋转对称性, 而忽略了系统晶格特征的微扰模型给出的结果为完全各向同性. 由于等效参数m非常小, 贝里曲率主要分布在两个谷点K和K′附近,在远离谷点时迅速衰减至零. 两个谷的贝里曲率正好符号相反, 因此, 其在整个布里渊区的积分等于零, 即系统的陈数为零. 然而, 由贝里曲率在单个谷点附近进行积分定义的谷陈数则可以不为零 图10 即对于K′和K两个谷点, 其谷陈数分别为+1/2和−1/2. 因此, 当通过不相等的质量mp≠mq使得系统对称性从C6v降至C3v时, 系统变为谷霍尔绝缘体, 其中mq>mp时为正谷霍尔相,mq 根据体边对应关系(Hasan et al. 2010), 不同拓扑相组成的界面上一定存在受拓扑保护的界面态. 根据导出的k·p微扰等效模型, 可以非常容易地解析验证界面态的存在性、传播方向及其极化特征等. 为验证根据以上蜂窝质量弹簧系统设计的谷霍尔绝缘体, 考虑由正、负两种谷霍尔相组成的界面(图11,x′ < 0,m> 0;x′ > 0,m< 0), 界面方向沿着y′呈现周期性, 界面左侧单胞中q质点质量较大, 而界面右侧单胞中p质点质量更大. 具体界面特征随角度θ不同而变化.θ= 0o对应于锯齿形(zig-zag)界面, 而θ= 30o则呈扶手椅(amchair)界面. 根据微扰等效模型式(20), 界面两侧介质中的弹性波传播规律由如下微分方程给出(即将等效哈密顿量中两种波矢做替换Δkx 图11 为了求解界面态解析表达式, 注意到界面在y'方向具有周期性, 则其界面态具有布洛赫解形式ψ(x,y) = (c1,c2)Texp(λ′x′) exp(iΔk′yy′), 其中c1和c2为待求解的未知系数. 将该表达式代入波动控制方程(27)可得 为获得非零解, 需要系数矩阵的行列式为零, 据此可得到特征频率以及特征模态 要使得特征模态局域在界面附近, 需要参数λ′x′ 在界面两侧均为负数, 使得特征模态沿法向远离界面时呈现指数衰减. 此外, 比例c1/c2在界面两侧必须连续, 即满足界面连续性条件. 注意到Δω/ω0和Δky′在界面两侧分别相等, 则可以非常容易验证, 存在如下指数衰减且满足线性色散关系的界面态 将K′和K谷态对应表达式代入上式, 可以得到p和q质点位移的具体表达式 可以看到, 界面态由之前的谷态组成, 外加指数衰减项及相位差因子. 从色散关系曲线式(30)可以清晰看出, 由谷点K′ 特征模态组成的界面态沿着−y′ 方向传播, 而由另一个谷点K特征模态组成的界面态则沿着反方向传播. 如果交换两个谷霍尔相的位置, 则对应关系将发生反转.还注意到, 指数衰减因子|m(x′)/v|与微绕模型中的等效质量相关, 即p和q质点质量差异越大, 界面态越集中在界面附近. 此外, 上述表达式表明, 对于任意的界面方位角θ均存在相应的界面态,这表明界面态具有一定鲁棒性. 以上解析表达式并不能直接反映弯曲的影响, 下文将通过数值算例验证界面夹角突然改变时界面态的鲁棒性. 图12 (a)(b)给出了两种谷霍尔相组成的条状界面(A:mp= 0.9,mq= 1.1; B:mp= 1.1,mq=0.9)以及对应的能带结构. 界面沿着y方向, 根据图11 (b)其对应于方位角θ= 0o. 在计算能带结构时, 条状几何的上下边界施加有布洛赫连续性条件. 在能带结构图中(图12 (b)), 灰色曲线代表体态, 在禁带范围内出现了一条由蓝色曲线代表的额外模态. 该传播模态对应于界面态, 从给出的位移场(图12 (c)−(e))可以看出. 对于界面态(图12 (d)), 只有靠近界面的质点具有很大的位移振幅. 从色散曲线亦可以得出, 在K′的界面态具有负的群速度, 与之前理论预期一致. 图12 为更清晰地看出界面态质点(图13 (a))的运动,图13 (b)(c)给出了靠近界面附近质点的运动轨迹. 对于谷点K′ 对应的界面态, 质点p/q分别按照逆时针/顺时针绕平衡位置运动, 和上述解析表达式一致. 对于谷点K对应的界面态, 所有质点的运动反向. 由于微扰等效模型为完全各向同性, 解析表达式(31)给出的质点轨迹为标准圆形, 实际上质点轨迹为主方向沿x或者y的椭圆. 这主要是由于真实系统仅满足C3v离散对称性, 而不是完全各向同性.q/p质点水平位移沿着x方向的分布如图13 (d)(e)所示, 其中的指数衰减规律和解析表达式(31)的预测高度一致. 图13 如前所示, 在谷霍尔绝缘体设计中, 关键在于如何使其频散曲线产生线性简并的狄拉克锥.之前部分的谷霍尔设计主要依靠布拉格散射相关的狄拉克简并, 相应的频率位置由晶格常数决定. 这意味着实现低频拓扑传输功能需要较大的晶格尺寸, 不利于实际应用需求. 这里介绍基于局域共振的谷霍尔绝缘体设计(Zhang et al. 2020), 基本思路为在满足C3v对称性的点阵中引入局域振子, 可产生频率位置由振子共振频率决定的狄拉克锥以及相应的谷传输拓扑界面态. 考虑如图14 (a)所示的弹簧质量离散模型. 该蜂窝点阵的代表单胞为灰色菱形所示, 其晶格常数取为单位1. 每个单胞内包含两个质量均为M的外部质点, 分别记作p和q.p和q内部各有一个局域振子(分别记作r和s), 其质量分别为mr和ms. 这里只考虑出平面极化振动模式, 因此所有质点均只沿出平面方向运动. 临近的外部质点由出面刚度为Kt的弹簧连接, 局域振子的出面刚度均为k. 该弹簧质量模型的第一布里渊区如图14 (b)所示. 图14 当β1=β2=β= (mr+ms)/2M时, 这四个特征频率两两简并, 即ω1=ω2且ω3=ω4, 分别与图15 (a)中的两个狄拉克锥对应. 可以较容易地证明得到,表明较低频狄拉克锥的频率一定小于局域振子的共振频率. 因此, 在不改变晶格常数的前提下, 可以通过改变局域振子的共振频率调节该狄拉克锥的频率位置. 当单胞中两个局域振子的质量存在小幅差异, 即0 < |β1-β2| <<β时, 由于两振子的共振频率不同, 狄拉克锥简并退化并形成新的带隙, 如图15 (b)所示. 图15 谷点(K或K′)附近的特征模态可由谷点处的特征模态线性组合近似表示. 参考第二节介绍的k∙p微扰等效方法, 可以得到该局域共振型谷霍尔绝缘体的等效模型为 基于上述弹簧质量离散模型, 可设计如图16 (a)所示的实体微结构模型(Zhang et al. 2020).将铝板(银白色部分,Eal= 70 GPa,ρal= 2700 kg/m3,υal= 0.33)局部镂空形成刚度弱化, 与附加铅柱(黑色部分,El= 17 GPa,ρl= 11 300 kg/m3,υl= 0.33)一起构成局域振子. 晶格常数为L= 3 cm,铝板厚度为h= 2 mm; 细梁的厚度和宽度分别为tb= 0.5 mm和hb= 1 mm; 铝板上镂空的圆孔半径为R= 7.5 mm, 铅柱的半径为r= 3.5 mm. 单胞中两个铅柱的厚度分别记为h1和h2. 图16 h1=h2= 2.0 mm时的频散曲线如图16 (b)所示, 颜色表征极化模式, 这里只关注颜色值接近于1的出平面极化振动. 可以看到, 在关注的频率范围内, 布里渊区角点K处存在两处狄拉克简并. 根据先前弹簧质量离散模型分析结果, 较高频处的狄拉克简并(简并2)与不含局域振子的蜂窝点阵所具有的简并一致, 相应的特征模态呈现布拉格散射特性. 另一个狄拉克简并(简并1)位于该模型的局域共振带隙正下方, 其特征模态表现出明显的局域共振特性, 表明该狄拉克简并的频率位置主要由局域振子的共振频率决定. 当h1= 2.3 mm且h2= 1.7 mm时, 该模型的频散曲线如图16 (c)所示. 由于单胞中两个局域振子的共振频率不同, 简并1退化产生带隙(蓝色区域). 同时,图16 (d)给出了该参数下模型的出平面等效密度. 可以看到, 在新产生的带隙频率范围内, 等效密度要么为负值要么为较大的正值, 具有明显的局域共振特点. 为了证明在由狄拉克简并1退化而形成的局域共振带隙范围内存在界面态传播模式, 进一步分析如图17 (a)所示的包含16个单胞的条带状超胞的频散特性. 该条带状超胞包含8个A型单胞和8个B型单胞, 其中,h1= 2.3 mm,h2= 1.7 mm. 相应的频散曲线如图17 (b)所示,蓝色色标对应出平面振动模式. 在单胞的拓扑局域共振带隙范围内, 观察到一条界面态传播模式, 如绿色实线标注所示.图17 (c)给出了f= 2500 Hz时的特征模态, 位移主要集中于靠近界面的局域振子上. 图17 下面研究上述界面态传播模式对拐角的免疫特性. 考虑如图17 (d)~图17 (f)所示的三种结构, 分别对应不包含界面、“直线”形界面路径、“Z”形界面路径, 均包含16 × 16个单胞. 对结构进行频域模拟, 四周施加低反射边界, 并在界面路径入口处施加频率为2500 Hz的简谐激励, 如红色波浪箭头所示.图17 (d)给出了不包含界面的结构的位移场, 由于带隙范围内不存在体态传播模式, 位移在远离激励源处迅速衰减. 对于含“直线”形界面路径(图17 (e))和“Z”形界面路径(图17 (f))的结构, 激发的弯曲波均可沿界面传播. 特别地,图17 (g)给出了图17 (e)中蓝色虚线上的振幅分布. 以界面处的振幅为参考, 振幅衰减为最大振幅的一半对应的宽度(FWHM, 即半高宽)为1.16L(L为晶格常数), 表明位移在远离界面方向迅速衰减. 此外,图17 (h)给出了三种结构在2375 ~ 3000 Hz范围的透射率. 可以看到, 在拓扑局域共振带隙范围内, “直线”形界面路径和“Z”形界面路径的透射率相当, 均远高于体态的传输率, 表明该界面态在一定程度上受拓扑保护.而在普通的局域共振带隙范围内, 除个别透射峰外, 三种结构的透射率均非常低. 在弹性波谷霍尔绝缘体实验研究方面, 目前已有不少相关工作(Vila et al. 2017, Pal et al.2017, Gao et al. 2021). 这方面的多数研究是基于布拉格散射系统, 即谷传输边界态的频率位置与晶格常数相关. 为了突破该限制, Zhang等(2020)制备了局域共振型谷霍尔绝缘体, 并通过实验研究在局域共振带隙中观察到了谷传输界面态传播现象. 此外, 针对当前研究中一旦设计的拓扑材料制备完成, 材料中允许传播的界面态路径是固定不变的这个问题, Zhang等(2019a)还设计了一种可编程谷霍尔绝缘体, 实现了可重构的界面态传播路径. 下面就这两方面展开具体介绍. 3.2.1 局域共振型谷霍尔绝缘体实验研究 相关理论设计及数值研究部分在3.1小节已作介绍, 下面主要介绍相应的实验研究部分. 制备的局域共振型谷霍尔绝缘体如图18所示, 材料参数以及微结构几何尺寸与图16 (a)所示模型一致. 结构中包含一条“Z”形界面路径, 如图18中红色实线所示. 界面两侧的单胞互为镜像, 如图17 (a)所示. 激振器置于结构背面, 探头垂直固定于黑色圆点所示位置. 图19 (a)给出了图18中A点和B点处的频响曲线. 其中, A点位于“Z”形界面路径上, B点位于界面一侧的材料体内. 可以观察到两个明显的低透射区域, 用灰色和蓝色矩形标注如图. 在灰色低透射区域内, A点和B点的透射率均非常低, 而在蓝色低透射区域内, A点的透射率较B点提升了约20 dB. 这意味着在蓝色区域频率范围内, 存在界面态传播模式. 因此, 结合图17 (h)中数值模拟给出的透射率曲线可以判定, 蓝色区域对应该局域共振型谷霍尔绝缘体的拓扑局域共振带隙, 而灰色区域对应其平凡局域共振带隙. 为了验证该结论, 利用扫描式激光多普勒测振仪记录了结构在三个代表性频率下的均方根速度场, 分别为1500 Hz(位于通带范围内)、2045 Hz(位于拓扑局域共振带隙范围内)、2500 Hz(位于平凡局域共振带隙范围内). 可以发现, 当激励频率位于拓扑局域共振带隙范围内时(图19 (c)), 激发的弯曲波沿“Z”形界面传播, 在远离界面方向迅速衰减. 而当激励频率位于平凡局域共振带隙范围内时(图19 (d)), 位移集中于振源附近, 未观察到传播现象. 作为参考, 激励频率位于材料通带范围内时(图19 (b)), 能量分布于整个结构. 图18 对比图19 (a)中的实验测量结果与图17 (h)中的数值模拟结果可以发现, 实验测得的带隙频率明显低于数值计算中的带隙频率. 该差异主要是由于材料制备造成的. 实验中, 基体铝板与局域振子是分开加工, 然后再用胶水粘接一起的. 因此局域振子的刚度相对数值模型要小一些,导致带隙位置向低频偏移. 为了验证这一点, 根据实验结果, 将数值模拟中微结构梁的厚度tb(图16 (a))调整为0.42 mm, 再次计算了图17 (a)所示条带状超胞的带结构, 如图20所示. 可以看到, 实验结果显示的带隙位置与超胞体带隙的位置吻合较好. 需要说明的是, 由于振子质量不变而刚度降低, 空间反演对称性破坏程度增强, 导致拓扑界面态(绿色实线)的带宽减小. 图19 图20 3.2.2 通路可编程谷霍尔绝缘体实验研究 为实现可重构的界面态传播路径, Zhang等(2019a)提出了一种可编程谷霍尔绝缘体, 其单胞由固体基体和液体夹杂(磁性流体)构成. 通过设计的可编程磁场控制系统, 可独立地调节每个单胞中的磁流体分布, 从而改变结构中拓扑界面态传播路径. 设计的正六边形蜂窝点阵如图21所示, 其代表单胞含有两个圆柱形空腔, 通过细小的拱形通道连通. 当单胞不含磁流体时, 根据3.1节介绍, 由于点阵材料同时满足C3对称性和空间反演对称性, 其频散曲线在K点处线性简并形成狄拉克锥, 如图21 (a)所示. 需要说明的是, 这里仅关注出平面极化振动模式, 即图中蓝色频散分支. 当单胞其中一个空腔充满磁流体时, 不对称的质量分布打破了点阵材料的空间反演对称性. 相应地, 蓝色频散分支上的狄拉克锥退化形成带隙(图21 (b)). 那么, 在该带隙频率范围内, 受拓扑保护的界面态可以沿着由具有相反质量分布的点阵构成的界面进行传播, 如图21 (c)所示. 利用设计的可编程磁场控制系统, 可独立调节每个单胞中的磁流体分布(图21 (d)), 进而可根据实际需要重构用于传播拓扑界面态的路径形状, 如图21 (e)所示. 图21 单胞几何参数如图21 (f)所示, 固体基体可由3D打印(打印机: Object 350, Stratasys, USA;耗材: RGD810, VeroClear, Stratasys, USA)而成, 黑色部分为磁流体夹杂. 固体基体的模量和密度分别为E= 2 GPa和ρ=1200 kg/m3, 泊松比为0.4. 单胞的晶格常数为L= 4.0 cm, 厚度为h=4.0 mm; 圆柱空腔的外半径和壁厚分别为8.6 mm和0.7 mm; 单胞两侧三角棱柱的边长为l=1.866 cm, 单胞之间连接处的宽度为a=L− 2l. 为了验证在图21 (b)中带隙范围内存在界面态传播模式, 进一步研究由16个单胞组成的条带状超胞的频散特性. 在COMSOL Multiphysics中建立如图22 (a)所示的条带状超胞, 包含8个磁流体集中于左侧空腔的单胞和8个磁流体集中于右侧空腔的单胞. 这两种类型单胞的连接处称之为“界面”. 数值计算中, 该条带状超胞的上下两端为自由边界条件, 左右两端为布洛赫周期性边界条件. 得到的出平面极化振动模式的频散分支如图22 (b)所示. 在体带隙范围内(约1226 ~1441 Hz)出现一条界面态频散分支, 如蓝色点线所示.图22 (c)给出了该超胞在1234 Hz下的特征模态, 位移集中分布于条带状超胞的界面处而在远离界面的方向迅速衰减, 呈现界面态特征. 图22 进一步, 对该含液体夹杂的可编程谷霍尔绝缘体的界面态传播进行了频域模拟.图22 (d)(e) (f)分别给出了16 × 16的有限尺寸结构在直线界面路径、“L”形界面路径、“Z”形界面路径下的稳态位移场. 模拟中, 结构四周施加低反射边界条件, 界面路径中间(蓝色圆点所示)施加频率为1234 Hz的简谐激励. 可以发现, 在不同界面路径形状下, 激发的弯曲波均沿着界面路径传播. 3D打印制备的包含16 × 16个单胞的测试样件如图23 (a)所示. 可以看到, 界面两侧单胞中的磁流体分布状态相反. 实验测得的直线形界面路径构型在1450 Hz下的出面位移场如图23 (b)所示, 激发的弯曲波只沿着界面进行传播, 在垂直界面的方向迅速衰减. 利用设计的可编程磁场控制系统(图24), 通过转移单胞中的磁流体, 可重构结构中界面态路径的形状.图23 (c)和23(d)给出了“L”形界面路径构型和“Z”形界面路径构型的出面位移场, 弯曲波沿着新形成的界面路径传播, 并且可很好地绕过拐角. 需要说明的是, 实验中观察到的界面态频率与数值模拟中的频率有一定差异, 这主要由于3D打印结构的几何尺寸与数值中的理想模型有偏差造成的. 此外, 实验测试样件是分块打印再用胶水粘接在一起的, 空腔的密封也使用了胶水, 这对整体材料属性也有一定的影响. 图23 图24 综上所述, 设计谷霍尔绝缘体的关键步骤是首先得到狄拉克锥简并系统, 然后通过降低对称性打破简并实现谷霍尔拓扑相. 代表性的设计方案是基于蜂窝或三角晶格系统在布里渊区角点的狄拉克锥, 利用镜像或反演对称破却设计出谷霍尔绝缘体(Pal et al. 2017, Liu et al. 2018). 弹性波谷霍尔绝缘体实验研究已比较成熟, 如Zhu等(2018)、Vila等(2017)都在蜂窝点阵板系统中验证了谷霍尔效应, 其中Vila等(2017)在蜂窝晶格其中一个格点附加额外的磁铁, 类似第3.1小节中两个格点具有不同质量. Gao等(2021)则设计了基于三角排布散射体的谷霍尔绝缘体, 并验证了界面态的拓扑保护特性. 由于线弹性理论的线性缩放特性, Yan et al.等(2018)设计了微纳米尺度的谷霍尔绝缘体, 并研究了不同界面夹角对弹性波束分波的效果. 前一节通过调节蜂窝质量弹簧系统的质量参数, 打破反演对称性已经实现了谷霍尔绝缘体,本小节将在相同的系统中设计实现陈绝缘体. 在之前背景中已经介绍, 实现陈绝缘体需要打破系统的时间反演对称性. 外加磁场常用于打破电子系统或电磁系统的时间反演对称性, 然而, 弹性波、声波等机械波与磁场几乎不耦合, 无法通过磁场打破时间反演对称. 针对这里的质量弹簧振动系统, 将通过科里奥利力(简称科氏力)打破时间反演对称性(Wang et al. 2015b, Chen et al.2019), 具体做法可将系统置于旋转基座. 将之前的质量弹簧系统置于旋转基座上(图25), 在与旋转基座固定的坐标系下分析质点的运动规律. 在此非惯性坐标系中, 运动质点受到虚拟的科氏力Fcori= − 2Ω× (mv)以及离心力Fcent=m|Ω|2r, 其中v和r分别为质点的速度与位置矢量. 假定旋转基座角速度较小, 则质点受到的科氏力占主导, 离心力可以忽略不计. 在频率为ω的简谐振动情况下, 科氏力等价为Fcori= − 2Ω×(mv) = 2iΩ× (ma/ω),a代表质点的加速度. 通过列出质点的运动方程可以发现, 该科氏力可以通过将系统的质量等效为厄尔米特形式加以考虑, 单胞内各质点质量等效为mp(I +γσy),mq(I +γσy), 其中因子γ= 2Ω/ω表示耦合强度. 图25 考虑单胞内两质点质量相等mp=mq=m0且科氏力效应较弱γ<< 1的系统, 根据之前微扰等效模型建立方法, 以简并系统在K′ (K)的特征态{u1(K′),u2(K′)}({u1(K),u2(K)})为基, 可以得到与式(21)完全相同的等效模型 注意到, 由于科氏力打破了时间反演对称,K′ (K)谷点的等效模型中等效质量m互为相反数. 且在旋转角速度Ω不为零时, 系统存在宽度为m的禁带. 类似之前, 可以计算得到低频分支对应的贝里曲率 此时, 两个谷K和K′携带相同的贝里曲率. 将贝里曲率在整个布里渊区内积分, 可以得到陈数,也即是贝里曲率在两个谷附近积分的和 当旋转基座的角速度不为零时, 系统的陈数就不为零, 表明系统构成陈绝缘体. 此时, 系统允许单向传播的界面态, 可以按照之前的解析方法验证. 考虑类似图11 (a)中陈绝缘体组成的界面(x′ <0,m< 0;x′ > 0,m> 0), 假定两侧结构在y′方向具有周期性后, 可得到界面态 从色散关系可以看出, 由K′ (K)谷态组成的界面态均沿+y′方向传播, 意味着界面态仅沿单向传播. 同理可以验证, 两种拓扑相交换位置后(x′ < 0,m> 0;x′ > 0,m< 0), 界面态沿相反方向传播.这种现象可以在物理上理解为, 旋转基座的引入打破了系统在上下的对称性, 使得界面波只能沿某一方向传播. 对于最一般的系统, 即单胞内两质点质量不等且存在科氏力时, 同样以简并系统在K′(K)的特征态{u1(K′),u2(K′)}({u1(K),u2(K)})为基, 亦可以得到与(21)完全相同的等效模型 当时间反演对称性及空间反演对称性同时被打破的时候, 根据两种对称性的破坏程度, 即旋转基座角速度大小和胞元内两质点质量差, 系统可以处于四种不同的拓扑相(图26 (a)), 其中两种为谷霍尔绝缘体, 另两种为陈绝缘体. 括号内数值为贝里曲率在谷点K′和K的积分, 陈数为两个数值之和. 参数处于A ~ D四个区域内部时, 系统为包含完全禁带的谷霍尔绝缘体或陈绝缘体. 当参数处于四个区域的边界时, 系统没有完全禁带, 不属于绝缘体. 此时, 第2、第3支色散曲面仅在谷点K′或K打开带隙, 在另一个谷点则仍保持简并, 如图26 (b)中给出的带结构曲线情况, 其中参数为mp= 0.95,mq= 1.05和Ω= −ω0/40. 这种现象源于旋转基座打破了系统的时间反演对称性, 对由质量差在K和K′引起的禁带产生相反的影响,K点附近的禁带由于旋转而拓宽了,K′附近的禁带则由于旋转而减弱. 图26 为了验证不同拓扑相的拓扑界面态,图27 (a)~图27 (f)给出了以上4种拓扑相(A:mp= 0.9,mq=1.1,Ω= 0; B:mp= 1.1,mq= 0.9,Ω= 0; C:mp= 1.0 =mq,Ω= − 0.05ω0; D:mp= 1.0 =mq,Ω= +0.05ω0)组成的6种锯齿界面对应带结构. 带结构通过求解图12 (a)中所示条状超胞波动方程得出, 其中上下边界施加有布洛赫连续性条件. 带结构中的蓝色曲线代表界面态色散曲线, 对于陈绝缘体C/D组成的界面, 可以看到两条界面态色散曲线, 而其它拓扑相构成的界面仅有一条界面态色散曲线. 在传播方向上, 谷霍尔绝缘体A/B组成的界面支持双向传播的界面态, 而在包含陈绝缘体的界面仅支持单向传播界面态(图27 (b)~图27 (f)). 需要指出的是, 由于自由空间可以看作平凡的绝缘体, 因此在陈绝缘体的边界也存在相应的边界态. 为了带结构曲线更加简洁, 以上图中并没有画出边界态对应的色散曲线. 图27 图28给出了弹性波在以上几种拓扑相组成的界面传播模拟结果, 红色表示面内位移振幅大,虚线表示界面位置, 虚线内外为两种不同的拓扑相. 为验证界面态的拓扑保护特性, 该界面特别包含了如110o和80o的剧烈转角. 在谷霍尔相A/B组成的界面, 弹性波可以沿着双向传播, 而在包含陈绝缘体的界面(图28 (b)~图28 (f)), 弹性波只能沿着单向传播. 数值模拟结果与之前的解析结果和带结构计算吻合, 而且证实了弹性波可以沿着任意界面完美传播, 而不会因界面拐角产生明显的后向反射或散射. 图28 以上单向拓扑界面态基于周期晶格材料, 其拓扑波传播特性分析以能带理论为基础. 而常规固体力学的研究则主要以柯西连续介质理论为框架. 若能通过连续介质理论对拓扑传播特性进行刻画, 并揭示材料等效参数对波动的影响, 对于拓扑材料的设计与优化将是非常有益的. 为了在经典柯西弹性理论中刻画单向传输界面态, 则必然需要对弹性理论进行适当的拓展, 引入相关的额外等效材料参数. 一种方式是将密度等效为Hermitian形式, 即ρ= {ρ, iα; −iα,ρ}, 物理上可将旋转陀螺嵌入弹性体来实现(图29). 下面将阐释, 此时材料界面波动性质可从连续介质力学角度去研究, 且在特定参数情况下也能出现单向界面态. 首先, 考虑如图29所示的复合材料. 基体为弹性固体, 夹杂为刚体, 其内部耦合一个转子系统. 刚体在运动过程中与转子发生相互作用, 产生耦合作用力. 转子对刚体的作用力可以等效为刚体具有手性惯性质量的陀螺力. 为了进一步量化手性惯性质量的大小(记为常数α), 下面以陀螺转子为研究对象, 推导该常数与已知给定物理量的关系. 首先建立如图29 (c)所示的直角坐标系Oxyz, 其中ψ,φ, 和θ分别代表相对于转子主轴的自旋角, 进动角和章动角. 忽略重力作用, 转子匀速转动时的运动方程为 图29 Mx,My,Mz分别为沿x轴,y轴和z轴的扭矩.I0=Ixx=Iyy,I=Izz代表转子沿对应轴的转动惯量.考虑小幅简谐运动情形, 章动角θ(t) =Θexp(iωt), 且|Θ| << 1. 假设进动角速度不变且转子没有受到沿x轴和y轴的扭矩, 即Mx=My= 0, 即转子和点阵结构仅发生面内耦合. 可以推导得到(Brun et al. 2012) 上式表明, 进动角速率和频率大小相等, 且自转速率和频率满足以上关系. 将上式代入式(41)可得 设转子的特征长度为h, 则转子顶端偏离z轴的位移和转子章动角之间满足U=hθ. 那么, 转子所受扭矩可表示为Mz=fhθ. 其中f为“陀螺力”, 方向垂直于时谐位移, 大小为虚数i表明陀螺力相对时谐位移有一个固定的相位差. 陀螺力的符号和转子的自转方向有关, 当自转方向变化时, 对应的符号也会改变. 这里可以记自旋常数为α=Ih−2. 由牛顿第三定律可知, 转子对点阵的反作用力为fg= ±iω2αU, 其对应的矩阵表达式为 那么, 夹杂在运动过程中的平衡方程为fext+fgyro= −mω2U,fext为弹性基体产生的外力 由此可知, 陀螺转子的作用相当于使得节点质量具有了陀螺惯性. 当节点做简谐振动时, 转子会耦合产生手性的陀螺力, 使得节点在平面内的振动由线偏振变为椭圆偏振. 此时, 由于系统的时间反演对称性被打破, 从而可以实现多种奇特的物理现象. 在长波极限下对陀螺复合材料进行均质化等效后, 可以从连续介质力学角度来分析边界态的特性. 对于一般的各向异性弹性介质, Stroh理论是求解瑞利波的经典方法(Stroh 1962). 当引入陀螺介质以后, 密度由标量变成了张量, 需要将Stroh理论进行适当推广, 才能给出弹性陀螺介质的非互易瑞利波解. 将等效陀螺介质的密度考虑为Hermitian形式, 即ρ= {ρ, iα; −iα,ρ}, 则弹性陀螺介质的运动方程为 对于半无限大空间, 陀螺介质位移场的一般表达式为 其中, 矢量m和n分别为表面切向和表面法向, 矢量x为空间位置. 当参数p的虚部为正值时, 表明波在传播过程中沿法向衰减. 在表面沿m方向传播的表面波波数为ξ, 相速度为v, 极化矢量为a. 极化矢量可以为复数, 代表模态轨迹为椭圆. 首先, 将式(47)代入式(46)可得关于p的广义特征方程 对于自由表面n∙x= 0, 将位移(47)代入表面力矢量t= (C:∇u)∙n可得 其中,l为表面力矢量幅值. 将式(48)和式(49)进行线性变换可得关于p的特征方程, 称之为Stroh特征方程 其中,p为特征值, [al]T为特征矢量,N为4 × 4的Stroh特征矩阵. 求解该特征方程可得到两对共轭特征值角标“+” 、 “−”代表了p的虚部符号同时也代表了表面波传播方向. 对应的特征分量分别为因此, 表面波的位移解可以显式给出, 沿m正方向的表面波解为 这里v> 0, 并且ξ=ω/v> 0. 沿m负方向的表面波解为 这里v< 0, 并且ξ=ω/v< 0. 相应的表面力为 当α= 0时,N为实数矩阵, 对应的特征矢量为共轭对, 即为共轭特征分量. 这种共轭特性决定了前向波和后向波是镜像对称的, 且具有相同的相速度. 当α≠ 0时,N为复数矩阵,不再是共轭对, 由式(54)得到沿两个方向的表面波波速出现差异, 甚至随着α的增加, 表面波仅支持单向传输(Zhao et al. 2020). 作为验证,图30给出了不同强度陀螺参数时表面波传播模拟结果, 激励形式为上下振动点激励. 在无陀螺效应时α/ρ= 0, 表面波在左右对称分布, 在向右传播的瑞利波中质点沿椭圆轨迹逆时针方向旋转, 反之则顺时针方向旋转. 在陀螺参数α/ρ= 0.5时, 自由体表面左右传播的瑞利波不再对称, 向右的瑞利波速度更快, 同时, 其椭圆形轨迹在x方向更宽. 当参数α为α/ρ=1.5和3.0时, 向左传播的瑞利波速进一步下降, 质点极化越发趋近于线极化剪切波模式, 而介质表面不支持像右传播的瑞利波. 图30 综上所述, 由于陈绝缘体需要打破时间反演对称性, 其在物理实现上比较困难, 潜在途径主要为以上介绍的两种: (1)引入旋转陀螺与系统耦合; (2)利用非惯性系中的科里奥利力. 两种方案在理论和数值上都得到了验证(Wang et al. 2015a, 2015b; Chen et al. 2018b, 2019). 在实验方面,Nash等(2015)设计了包含陀螺效应的离散质量弹簧点阵系统, 演示了霍尔绝缘体具有的单向传输边界态特性, 并且发现通过改变点阵构型可以调控单向态传输方向. 在连续系统中的实验研究还未见报道. 本小节将介绍如何在2.2小节蜂窝系统中设计实现自旋霍尔绝缘体. 在经典波系统中实现类似的自旋霍尔效应, 关键在于构造赝自旋态以及相应的双重狄拉克锥简并. 在此, 利用Wu等(2015, 2016)首先提出的超胞方法, 来设计实现弹性波自旋霍尔绝缘体. 下面以前面的蜂窝弹性系统为例, 介绍该方法基本设计机理. 如图31 (a)所示, 在所有质量均相等(m0= 1)的蜂窝点阵系统, 图中六边形所示区域即为一个胞元, 其中质点按照顺时针方向从1编号到6. 同一个胞元之间的质点由刚度为ti的弹簧连接,而连接不同胞元间的质点的弹簧刚度系数则为to, 分别用于调节胞内耦合(intra-cell coupling)、胞间耦合强度(inter-cell coupling). 第一布里渊区如图31 (b)中灰色六边形区域所示. 当胞元内弹簧和胞元间弹簧刚度相等时ti=to, 最小单胞为图31 (a)中的菱形区域所示, 其对应的第一布里渊区应如图31 (b)中绿色六边形. 在这种情形下, 布里渊区角点K′和K′′出现简并频率相等的两个狄拉克锥. 考虑到ΓK′和ΓK′′为图31 (a)中六边形胞元对应的倒格矢量, 则布里渊区角点K′和K′′处的两个狄拉克锥被折叠到Γ形成双重狄拉克锥, 这为构造赝自旋态提供了基础. 图31 下面对系统的波动规律进行分析. 一个单胞包含6个质点, 对应有12个平动自由度. 按照第2节中的方法建立系统布洛赫波传播方程, 可以得到一个12维矩阵表示的特征值问题. 由于质量矩阵和刚度矩阵非常繁琐, 这里就不详细列出. 该特征值问题一共可以求解出12支色散曲线,但此处主要关注在Γ处简并的几条色散曲线. 对于弹簧刚度系数不相等的一般情况ti≠to, 第5到8支色散曲线在Γ处两两简并在一起, 而当刚度相等ti=to=t时则形成双重狄拉克锥简并, 对应的特征模态及频率给出如下 以上四个特征模态p1,p2,d1,d2按照质点编号1到6的顺序依次给出x方向和y方向的位移. 注意到各质点的位移分量均为实数, 其对应的振动形式为质点经过其平衡位置做线极化振动(图31 (c)).p模态场在空间反演操作下呈现反对称, 而d模态场在空间反演操作下对称. 这种对称性正好与原子p和d轨道波函数对称性类似, 因此取名为p和d特征模态.p/d特征模态的对称性及简并特征本质上源于系统特定的对称性, 即C6v对称群, 该点群正好包含两个不可约的二维表示. 虽然以上质量弹簧系统并不包含内秉自旋自由度, 但根据以上求解的特征模态及系统具有的对称性, 可以构造赝自旋及对应的反演算符(Wu et al. 2015) 这里, 符号+/-用于表示上/下自旋(pseudo spin-up/spin-down),K代表复共轭算符. 对于由p模态构成的上/下自旋态, 胞元内的质点均逆时针/顺时针绕其平衡位置做圆极化振动; 而由d模态构成的上/下自旋态中质点的圆极化振动方向正好相反. 可以容易地验证, 当赝时间反演算符作用于构造的赝自旋态时, 自旋方向发生改变同时出现180o的相位变化, 这一点和时间反演算符作用于电子自旋自由度的效果一致. 对于刚度系数差异较小的情况, |ti−to| << 1, 采用之前推导微扰等效模型的方法, 以上述四个自旋态{p+,d+,p−,d−}作为基, 可以得到系统在Γ的等效哈密顿量 其中,h+(k)/h−(k)代表与上/下自旋对应的哈密顿量,ψ为由上下自旋表示的特征向量. 参数δt,B和A分别称为狄拉克质量, 自旋轨道耦合系数及狄拉克速度. 注意到上下自旋相互解耦, 可以根据h+(k)ψ+= Δωψ+和h−(k)ψ−= Δωψ−分别求解出相应特征模态, 进而得到一对二重简并解 高频分支和低频分支各自由上自旋和下自旋两个解构成, 记作为ψ+/ψ-, 其展开基为{p+,d+}/{p−,d−}. 高低频分支间的带隙大小为|2δt|, 当刚度相等ti=to时带隙关闭. 按照之前惯例, 这里同样关注低频分支, 根据上/下自旋态解式(61), 可以求解得到对应的贝里曲率 上/下自旋对应特征模态具有相反的贝里曲率. 按照定义, 将自旋态的贝里曲率在布里渊区积分,可以得到各自旋分支的自旋陈数 系统的陈数等于上下自旋陈数相加, 仍然为零, 这和系统满足时间反演对称性一致. 但自旋陈数本身却可以不为零, 表明系统可以实现自旋霍尔绝缘体. 当参数B和δt的正负符号相同时, 即B×δt> 0, 系统为自旋霍尔绝缘体, 反之则为平凡绝缘体. 注意参数B始终为正, 则当刚度参数跨越临界点ti=to时, 系统将产生拓扑相变. 当胞元间弹簧的刚度较大时, 满足B× δt> 0, 上述蜂窝质量弹簧系统为自旋霍尔绝缘体. 上述自旋霍尔相变也可以由带结构反映.图32给出了三种参数情形下系统对应的能带结构(ti= 1.05 >to= 0.90;ti= 1.0 =to;ti= 0.95 图32 为了验证自旋方向依赖的界面态, 同样考虑平凡绝缘体和自旋霍尔绝缘体构成的界面, 并解析求解相应的界面态, 假定界面构成类似之前图11(x′ < 0, δt< 0;x′ > 0, δt> 0). 为了简化分析, 仅保留微扰等效模型式(58)中的一阶近似项, 忽略二次项, 即不考虑自旋轨道耦合效应, 这在波矢足够小|k| << 1时有效. 完全按照先前的分析, 通过连续条件可以得到上/下自旋对应界面态(Shen 2017), 界面态ψ+由上自旋态p+和d+态构成, 界面态ψ−则由下自旋态p−和d−态构成. 两个自旋相关的界面态具有线性色散关系, 其相速度均为A, 但传播方向相反. 因此, 通过施加下(上)自旋激励, 可以选择性地激发出只沿着界面向上或向下传播的界面波, 称为自旋锁定界面态. 当左右交换自旋霍尔绝缘体和平凡绝缘体的位置后, 相应界面态的传播方向反向. 通过条状几何超胞带结构计算, 也可以验证上述自旋锁定的界面态.图33 (a)给出了由左侧自旋霍尔绝缘体(to= 1.10,ti= 0.95)和右侧平凡绝缘体(to= 0.90,ti= 1.05)组成的条状超胞, 界面沿y方向, 相当于图11中的θ= 0o界面方向.图33 (b)给出了计算得到的带结构曲线. 在带隙区域, 可以清楚地看到两条斜率相反的界面态, 其对应的振动模态如图33 (c)所示, 仅界面附近的质点有较强振动.图33 (d)(e)给出了界面附近质点振动轨迹示意图. 按照式(64)预期, 对于θ= 0o方向的界面, 质点振动为线性极化, 这里质点的振动轨迹非常接近于线极化. 图33 通过人为的施加上/下自旋激励, 可以产生单向传播的弹性波, 瞬态数值模拟结果如图34所示. 其中自旋霍尔绝缘体(to= 1.10,ti= 0.95,m0= 1)与平凡绝缘体(to= 0.90,ti= 1.05,m0=1)组成与之前类似的复杂弯曲界面. 在数值模拟中, 激励源处胞元内质点的激振位移按照自旋模态p+或p−施加, 并由时域高斯脉冲信号exp(−(ω0t/80)2) × cos(ω0t)调制, 且激励中心频率ω0=2π/T0处于带隙范围. 在上自旋激励中(图34 (a)(b)), 1到6号质点顺时针围绕平衡位置作圆极化振动, 振动幅值相同相位依次相差120o, 激发产生的弹性波只能沿着界面顺时针方向传播, 而且完美绕过界面拐角而不产生散射或反射. 当采用下自旋模态激励时, 界面态将沿反方向传播(图34 (c)(d)). 图34 需要指出的是, 以上自旋锁定的界面态出现在自旋霍尔绝缘体与平凡绝缘体组成的界面. 如电子自旋霍尔绝缘体一样, 这里的弹性波自旋霍尔绝缘体也支持自旋锁定的边界态, 但其鲁棒性不如具有内秉自旋的电子自旋霍尔绝缘体. 本质原因在于赝自旋态由超胞的布洛赫模态构建, 与超胞的C6v对称性密切相关, 破坏C6v对称性会破坏赝自旋态. 为了在自旋霍尔绝缘体边界观测到自旋锁定的边界态, 需要边界处胞元保持局部C6v对称性, 否则将无法观测到自旋边界态. 如图35 (b)所示, 当边界按照完整胞元截断时(图35 (a)), 带结构曲线中出现无能隙的边界态, 而当边界截取为不完整胞元时(图35 (c)), 边界不支持传播模态(图35 (d)). 图35 以上单向波传播现象来自于构造的赝自旋态. 实际上, 经典弹性波中也存在类似的自旋霍尔自由度. 例如, 弹性体自由表面的瑞利波, 其质点振动轨迹一般为椭圆 (图30), 表明瑞利波携带有内在的自旋(Long et al. 2018), 且沿界面向左右传播的瑞利波质点振动方向相反(图36 (a)). 在弹性体界面施加圆极化的的振动, 可以产生类似的自旋锁定传播现象(图36 (b)). 需要注意的是,瑞利波携带的自旋来源于物理场本身, 容易发生散射, 对缺陷和路径弯曲的鲁棒性较差. 图36 压电等主动控制技术常被用在弹性波传播控制中, 但与拓扑波动结合的研究不多. 相较于基于结构设计实现狄拉克简并, Li等(2020)给出了一种利用压电主动控制实现双重狄拉克锥的方法.图37是其设计的六边形蜂窝单胞, 角上覆盖有压电片, 可与包含负电容的电路连接. 在压电电路断开时, 系统在2200Hz左右形成两条双重简并能带, 在负电容介入电路后, 四条能带完全简并形成双重狄拉克锥. 这与调节参数实现的偶发四重简并有类似之处, 不同点在于这里的调节参数为电路参数. 进一步利用压电主动控制, 或可实现材料在平凡绝缘体和自旋霍尔绝缘体之间切换. 图37 在固体弹性系统中, Yu等(2018)首次实现了弹性波类量子自旋霍尔效应, 验证了界面态对缺陷和拐角免疫性. 基本设计思路也是利用超胞构造赝自旋态. 构建如图38 (a)所示的蜂窝点阵穿孔板, 单胞内包含6个等大小的孔洞, 通过调节相互距离, 可调节胞元内、外的耦合强度. 当b=a0时, 布里渊区原点处出现两对双重简并(记为px/py和dx2 −y2/dxy), 两对简并频率之间为出面振动模式的完全带隙. 当b= 1.12a0时, 两对双重简并仍然存在, 不过相应的模态发生翻转, 即p和d模态的位置对调而两者之间的带隙位置基本不发生变化(图38 (a)). 在这两个构型之间,当b= 1.087 3a0时, 带隙完全消失, 两对双重简并合为一个具有四重简并特性的双狄拉克锥, 表明构型b=a0对应的绝缘体和b= 1.12a0对应的绝缘体之间需要发生拓扑相变才能相互过渡. 与之前类似, 由这两块绝缘体形成的界面上, 存在与赝自旋pseudospin+和pseudospin-对应的界面态(图38 (b)), 由具有双重简并特性的p和d模态组合而成(图38 (c) (d) (e)). 图38 图39 (a)~图39 (d)为不同类型界面传输特性的数值模拟和实验测试结果, 黄色虚线表示由拓扑非平凡绝缘体和普通绝缘体构成的拓扑非平凡界面. 数值模拟表明, 无论是界面存在“空位”缺陷(图39 (b))、“位错”缺陷(图39 (c))或是大幅拐角(图39 (d))情况, 弹性波均能良好传导.此外,图39 (e)给出了实验测量的上述四种类型界面路径的传输率. 图39 基于上述拓扑界面的缺陷免疫特性, Yu等(2018)还设计了任意形状的弹性拓扑环形谐振器, 用于弹性能的收集与释放. 所构建的基于“回音壁模式”的环形谐振器如图40 (a)所示, 包含一条平直界面波导和一个位于波导附近的环形谐振器. 在平直波导下端激发pseudospin+赝自旋态的出面弹性波并向上传输.图40 (c)给出了实验测量的环形谐振腔中的能量频谱, 可观测到两个谐振峰, 相应的谐振频率关于狄拉克频率(波矢k= 0处)对称分布, 如图40 (b)所示.在这两个谐振频率处, 环形谐振器与旁边的平直界面波导发生“临界耦合”. 由于拓扑绝缘体边界具有“自旋−动量锁定”的特性, 由其构成的“波导−环形谐振器”系统中的“临界耦合”将具有独特优势. 如图40 (d) (e)所示, 当处于回音壁模式的环形谐振器与平直波导发生“临界耦合”时, 能量几乎完全分布于环形谐振器中. 也就是说, 拓扑绝缘体边界构成的环形谐振器将如同一个能量“黑洞”−只有能量流入, 而无任何能量流出. 综上所述, 在弹性波系统中设计自旋霍尔绝缘体, 主要难点在于构造双狄拉克锥简并以及赝自旋态. 归纳现有方案主要有两种: 一是利用薄板中的对称模态与反对称模态作为基础, 通过参数调节获得两种模态偶发简并的双重狄拉克锥(Mousavi et al. 2015), 从而据此设计自旋霍尔绝缘体, Miniaci等(2018)给出了这种思路的实验验证; 第二种更普适的方法是利用5.1节已经介绍的超胞能带折叠机理, 将蜂窝系统布里渊区角点的狄拉克锥折叠至原点形成双重狄拉克锥(Wu et al. 2015; Chen et al. 2018b, 2019), 这也是目前大部分弹性波自旋霍尔绝缘体实验采用的思路(Yu et al. 2018, Cha et al. 2018, Chaunsali et al. 2018). 弹性波谷极化拓扑态和赝自旋拓扑态的拓扑属性由整数拓扑不变量和体能带结构的贝里相决定, 遵循体边对应原理. 近期研究发现, 打破无带隙边缘能带的拓扑相, 使其转化为具有带隙的平庸边缘能带, 则在其带隙内生成了体极化(bulk polarization)属性定义的高阶拓扑相(higherorder topological phase) (Benalcazar et al. 2017). 不同于传统一阶拓扑态, 高阶拓扑态出现在边界的边界. 对于二维拓扑系统, 高阶拓扑态出现在结构角点; 对于三维拓扑系统, 高阶拓扑态出现在结构的棱边和角点. 在机械(Fan et al. 2019, 2020; Tong et al. 2020; Serra-Garcia et al. 2018; Wu et al. 2020)、声学(Ni et al. 2019, Zhang et al. 2019b, Zheng et al. 2020)等系统, 研究人员成功观察到了高阶拓扑态. 在弹性波动系统中, Fan等(2019)通过实验研究在弹性声子晶体板中观察到了拓扑角态. 下面对该研究展开具体介绍. 考虑如图41 (a)所示的复合元胞, 其包含6个节点. 复合元胞周期性阵列组成图41 (b)所示的蜂窝弹性声子晶体板. 弹性板材料参数为密度ρ= 1190 kg/m3, 泊松比ν= 0.35, 杨氏模量E=3.2 GPa. 蜂窝弹性声子晶体板的厚度为d= 1.98 mm, 横梁的宽度和长度分别为w= 5.02 mm和L= 15 mm. 蜂窝弹性声子晶体板的节点上下表面各附着一个磁铁, 如图41中浅蓝色圆柱所示.磁铁的密度、泊松比和杨氏模量分别为ρ= 7400 kg/m3,ν= 0.28和E= 41 GPa. 磁铁的高度和半径分别为h= 2.0 mm和r= 2.51 mm. 磁铁作为附加质量块和横梁组成局域共振结构. 复合元胞的内部耦合强度定义为胞内耦合1/lintra. 相邻复合元胞之间的耦合定义为胞间耦合1/linter. 胞内耦合和胞间耦合的强度可通过调节横梁的长度lintra和linter来灵活调控. 图41 依据长波假设理论, 该弹性声子晶体板可以近似为薄板结构. 采用COMSOL Multiphysics 软件的固体力学模块计算复合元胞的能带结构时, 周期性边界条件施加于复合元胞的所有边界. 由抛物线色散描述的面外波动模式与面内波动模式是弱耦合的, 因此, 面外能带(红线)与面内能带(灰色线)彼此独立. 在本小节, 忽略了超出研究范围的面内波动模式, 主要考虑面外波动模式.当linter=lintra时, 弹性声子晶体板在不可约布里渊区(Brillouin zone)的Γ点出现了一个双狄拉克锥, 如图41 (c)所示. 双狄拉克锥由四个能带线性简并而成. 当lintra降低到0.836L, 与此同时linter增加到1.328L时, 双狄拉克锥打开产生了1461 Hz ~ 1650 Hz的完全带隙, 如图41 (d)所示.相反, 当lintra增加到1.2L, 而linter减小到0.6L时, 双狄拉克锥被打开生成了1503 Hz ~ 1715 Hz的完全带隙. 因此, 当复合元胞收缩(lintra 图42 图43 (a) (b) (c)为三个具有37个复合元胞的正六边形实验样件. 第一个正六边形样件是由膨胀复合元胞(lintra>linter)组成的平庸样件, 其本征频率如图43 (d)所示. 数值模拟时, 自由边界条件施加于样件的边缘. 该样件的本征模态只有体模态, 没有边缘模态. 第二个正六边形样件是由收缩复合元胞(lintra 图43 采用激光切割技术加工1.98 mm厚的亚克力板制备弹性声子晶体板样件. 用HEV-20型激振器对样品进行激励. 激振器顶杆的直径为4 mm, 紧贴于面板表面. 用多普勒激光测振仪(LVS01)扫描位移场. 由于测振仪的激光束垂直于面板, 因此只捕捉到垂直位移分量(即面外波能量). 位移信号由LMS-SCADAS测试系统记录. 平庸正六边形样件的体(黑色)、边缘(绿色)和角(红色)传输谱如图44 (a)所示. 对于体传输谱, 采用激振器激励样件内部的某一个节点, 并采用激光多普勒测振仪测量样件内部其他节点的位移响应. 对于边缘传输谱, 采用激振器激励样件底部边缘的某一个节点, 并采用激光多普勒测振仪测量底部边缘其他节点的位移响应. 对于角传输谱, 采用激振器激励样件的某一个角点, 并采用激光多普勒测振仪在同一角点测量位移响应.从图44 (a)可知, 在整个带隙内, 体、边缘和角的传输都很低, 这表明在平庸正六边形样件中, 弹性波的传播被声子带隙有效阻断. 拓扑正六边形样件的体(黑色)、边缘(绿色)和角(红色)传输谱如图44 (b)所示. 从图44 (b)可知, 体传输谱在低频和高频体区观察到由完全带隙隔开的峰值, 而在完全带隙内传输效率较低. 边缘传输谱在1610 Hz左右观察到一个峰值, 与图43 (e)中预测的边缘模态相匹配. 如图43 (e)中所示, 拓扑正六边形样件的拓扑角态和平庸角态非常接近.因此,图44 (b)角传输谱的拓扑角态和平庸角态重叠成整体, 形成1550 Hz左右的峰值. 图44 图45 (a)为收缩复合元胞(lintra 根据图43正六边形样件和图45正三角形样件的不同角态可知, 受拓扑保护的角模态只出现在2π/3的钝角处, 而不出现在π/3的锐角处. 为了解释这一现象, 引入拓扑指数N=|N+−N−|.拓扑指数N描述体哈密顿量的拓扑结构和缺陷的拓扑结构之间的相互作用, 被定义为角点的稳定模式数(Noh et al. 2018). 拓扑角模, 也称为“零模”, 是手征对称算符Π的本征态(Bao et al.2019).N+和N−用于计算拓扑电荷为+1和−1的Π的本征态数. 手征对称算符Π满足 图45 H(k,r)是哈密顿量的一种分类, 推广了体边对应原则, 将体哈密顿量的拓扑结构与缺陷的拓扑结构联系起来(Altland et al. 1997, Teo et al. 2010).k定义为d维布里渊区,r定义为环绕在D维表面的缺陷(即本节描述的角点). 在π/3锐角处, 有四种零模式, 如图46 (a)所示. 其中两种模式具有拓扑电荷+1, 另两种模式具有拓扑电荷−1. 因此, 拓扑指数为N=N+−N−= 2 -2 = 0. 这意味着锐角处没有稳定模式(图45 (c)). 在2π/3钝角处, 有三种零模式, 如图46 (b)所示. 其中两种模式具有相同的电荷, 另一种角模式具有相反的电荷. 因此, 拓扑指数为N= |N+−N−| =|1 − 2| = 1, 即稳定模式可局限于钝角处(图43 (e)). 图46 孤立波(solitary wave)是一种空间局域的、形状保持不变且单向稳定传输的非线性波包(Russell 1845). 而孤立子(soliton)则是一种具有强健稳定性的孤立波(Russell 1845). 从物理学的角度, 孤子是由系统非线性效应与色散现象相互平衡而产生的一类稳定的空间相干结构(拟序结构), 彼此碰撞前后能量不色散、波形与速度保持不变而具有准粒子属性(Dauxois 2006). 从数学的角度, 它是一类描述可积系统的非线性微分方程(如KdV, NLS, Toda, Sine-Gordon以及φ4方程等)的稳定孤波解(Dauxois 2006). 孤子因其在耗散介质中稳健传输的局域化特性, 以及拥有着在物理、化学和生物等系统中跨时空尺度传递信息和能量的潜力, 引起了众多领域科学家们的广泛关注(Dauxois 2006,Remoissenet 2013). 孤子理论作为非线性科学重要而活跃的分支, 不但推动了部分传统数学理论(如可积系统)的发展, 更在刻画和揭示自然科学现象的本质中发挥着重要作用: 如晶体中的位错、铁电体中的畴壁、聚合物的导电、长约瑟夫森结的磁通子、化学反应扩散、以及DNA和蛋白质等生物系统的非线性激发等(Dauxois 2006). 对于实际的力学系统, 耗散与色散普遍存在, 严重阻碍了机械信号(尤其是谐波等)的长距离稳定传递. 随着孤立子等研究热潮的兴起以及超材料的可设计性优势, 激发了力学家们对耗散系统中局域化波包的激发与传输的探索. 在力学超材料系统中, 孤子通常表现为局域化的应变波包或稳健的非关联实体(Dauxois 2006). 例如, 借助Hertz接触及其类比思想, 人们在颗粒介质、张拉结构、折纸超材料等中激发出孤立波(Nesterenko 1983, Daraio et al. 2006, Fraternali et al.2014, Yasuda et al. 2019). 此外, 基于突跳相变中畴壁的运动和相应的能量补给, 分别在磁关联的双稳态超材料以及3D打印的软质双稳态超材料链中实现了局域化的力学信号在耗散系统中的单向稳定性传输(Nadkarni et al. 2014, 2016; Raney et al. 2016). 相对于孤立波(稳定性可由系统耗散与非线性的动态作用来支撑), 力学超材料中孤子的激发, 其数学物理条件则相对苛刻: 控制方程解析解, 系统色散与非线性的恰当平衡. 尽管如此, 通过类比弹性波的极化特征, 人们在软质超材料中激发了兼具平动与转动极化, 并可由二次非线性Klein-Gordon方程所刻画的矢量孤子(Deng et al. 2017), 并基于三次非线性Klein-Gordon方程, 研究了一维矢量孤子的幅值带隙、反常碰撞与反射等一系列性质(Deng et al. 2018, 2019a), 同时还探索了一维超材料中的周期性矢量孤子(Mo et al. 2019)和二维软超材料中矢量孤子的聚焦和模式分离等行为(Deng et al. 2019b). 与以上平凡的孤子激发相对应, 在场论中还允许非平凡的孤子激发, 即拓扑孤子(topological soliton) (Manton et al. 2004). 拓扑孤子激发的一个必要条件是势能面有简并基态(真空)的存在, 亦即在无穷远处的空间可存在不同的简并基态和边界条件. 而非拓扑孤子的激发则不要求基态简并, 其解(无论是否为孤子解)在无穷远处都有相同的边界条件(如钟形孤子). 从场论观点来看, 尽管孤子都是相应经典场的非平庸解, 然而, 不同孤子其稳定性的来源却截然不同(郭柏林1987, Manton et al. 2004): 非拓扑孤子的稳定性主要由场组态的动力学机制来实现, 它源自于Nöether定理下的守恒量(Nöether荷); 拓扑孤子则是基于非Abel规范理论, 描述其的拓扑守恒量与Lagrange函数的不变性无关, 而是源于场的内禀自由度, 对应于内禀空间流形间的非平凡映射. 由于非Abel规范理论中非线性场方程的复杂性, 拓扑孤子目前仅在一些特定数学结构中得以求解, 如1D空间的扭结解(kink), 2D空间的涡旋解(vortex), 3D空间的‘t Hooft磁单极子解(monopole)以及4D欧氏空间的Polyakov瞬子解(instanton)等(郭柏林 1987, Manton et al.2004). 相比于抽象的数学诠释, 机械系统中拓扑孤子的激发则相对直观, 且较常见的是1D空间. 早期的如Scott单摆链模型(Scott 1969), 在此系统中可激发出非拓扑孤子、由Sine-Gordon方程描述的kink/antikink拓扑孤子和多(周期)孤子等(图47 (a)). 随后, 人们又在类摆链装置中系统研究了kink孤子的碰撞、动态性能, 以及kink-antikink晶格(周期孤子)、紧孤子(compaction)和扩散孤子(diffusive soliton)的激发等(Dusuel et al. 1998) (图47 (b)). 此类kink型拓扑孤子(晶格), 其非平凡特征可在拥有多重或双重简并基态的系统能谱空间中, 加以形象刻画(图47 (c)(d)). 最近, 力学超材料的兴起, 再一次将人们在力学系统中探索拓扑孤子的热情推向了新的高度. 较早吸引学者兴趣的有一维SSH超材料链(Chen et al. 2014, Zhou et al. 2017, Sato et al. 2018)、极小曲面和弹性条带等中的拓扑孤子激发(Machon et al. 2016, Bartolo et al. 2019,Sun et al. 2021). 代表性工作如Chen等(2014)实现的分别由φ4和Sine-Gordon方程描述的翻转与旋转式拓扑孤子, 其可由镌刻在3D圆环上构型空间的拓扑结构来分类(Chen et al. 2014). 随后, Snee等(2019)也在二维拓扑力学超材料中激发出拓扑保护的边界孤子, 其本质是由二阶NSL方程所描述的亮孤子(bright soliton)与暗孤子(dark soliton). 图47 事实上, 尽管孤立波与孤立子−时空局域化的非线性物态, 已在机械系统以及力学超材料中得到了实验激发和一定程度的探索, 然而当前报道的结果却表明, 它们普遍呈现出位置随机、尺度无关的离散或单孤子状态, 依然是众所周知的难以控制. 这使得, “如何开发拓扑结构去‘冻结’和控制孤子, 进而实现有序局域化变形的调控?”仍旧是一个长期以往的充满挑战的问题. 这里将以一类软质多孔力学超材料为例, 介绍静态拓扑孤子晶格的激发以及编程有序局域变形的普适性物理框架(Zhang et al. 2019c, 2019d). 构建一类多孔力学超材料如图48 (a)所示, 其元胞由正交的椭圆通孔在软质基体中阵列而成(图48 (b)). 其中, 该软质介质可由Mooney-Rivlin不可压超弹性本构方程描述. 为表述方便,此处定义无量纲参数来表征它的几何特征. 通过上述无量纲参数的连续变化就可得到超材料的一个丰富的几何空间. 这里关注于κ与1的大小关系, 并以此将该几何空间分类. 在Oxy面内, 对超材料施加沿y方向的准静态位移压缩(图48 (c), 实验中结果表明(Zhang et al. 2019c, 2019d),κ< 1和κ> 1的超材料将发生平凡激发, 分别表现为宏观均匀的正、负泊松比变形; 而κ= 1的超材料却发生了非线形拓扑激发, 表现为规则有序的局域变形(图48 (d)(e)). 可以在统一框架下(任意κ)建立理论模型, 在能谱(状态)空间中揭示支配两类激发的内在因素以及有序局域变形的物理本质. 图48 为针对此类代表性元胞建立统一的解析模型(图49 (a)), 考虑极端情形在位移载荷±uy作用下, 变形构型的应变能则主要集中于孔间的颈带处, 可由弹性杆的伸缩(刚度K)、颈部弹簧的弯曲(刚度Cv,Ch)与剪切(刚度Cs)来刻画(图49 (b)). 假定元胞初始倾角为θ0,当前构型倾角为θ, 则可定义转角α=θ−θ0为序参量来定量表征元胞的变形状态(图49 (b)).在给定应变εy下, 代表性元胞的应变能泛函可表示为Ucell(κ;αn) (图49 (c)). 基于实验与模拟结果可知, 当模型尺寸Ny/Nx<< 1时, 变形构型独立于尺寸Ny(图49 (d)(e)), 超材料可简化为Ny= 1的准一维结构(图49 (d)). 考虑元胞间的相互作用, 系统的Lagrangian可表示为在位移加载过程中, 原位势Ucell的形式逐渐演化, 而系统的变形构型则取决于元胞间相互作用能与原位势Ucell的竞争, 这一物理过程可由置于原位势场且彼此相互作用的“球−链”模型形象地描述(图49 (e)). 在变形许可的构型/状态中, 实际构型则使得系统L取极小值. 由最小势能原理可得离散控制方程(Zhang et al. 2019d) 图49 基于该控制方程,κ≠ 1时, 在所考虑的应变范围内(如|εy| < 0.2),Ucell关于α非对称且仅存在物理上允许的唯一基态(图49 (c)).κ= 1时,Ucell关于α始终对称, 且随εy演化将由初始的单一基态分岔为简并的双基态(图49 (c)(e)). 总之,κ主导了原位势和控制方程关于序参量α的对称性及其能谱空间Ucell(α;εy)中的分岔点数, 从而支配了超材料稳态演化路径和(非)平凡激发的必要条件. 进一步可知,κ≠ 1的超材料其宏观均匀变形本质上对应于控制方程平凡解αn=α0(n=1, 2, ···,Nx; ∂Ueff(α;εy)/∂α|α=α0=0)(Zhang et al. 2019d). κ= 1超材料的有序局域变形对应于非平凡激发. 此时,α=θ. 为进一步得到控制方程的解析形式, 这里引入两个基本假设: 假设(1) 小转角假设θn<< 1 (n= 1, 2, 3, ···) 若 具有唯一基态θn= 0. 在整个所考虑的应变范围内,超材料结构均由“拉压”主导, 仅发生纯压缩变形的平凡激发. 以λφ4方程为例, 可定义非平凡的拓扑荷(扭数)Q来对孤子进行拓扑分类, 它是流Jv守恒的结果, 即则(郭柏林 1987, Dauxois et al. 2006) 对于kink(antikink)有Q= +1(−1), 为非平凡映射; 对于基态则有Q= 0. 由于基态简并, 两个基态可在θ→ −θ反射下相互转换, 而Kink则嵌入在x= ±∞处的两个基态之间, 并与其在无穷远处趋近. 基于拓扑荷的守恒性, 场的拓扑约束可视为一无限的位垒, 因此场组态kink与antikink的相互转换抑或耗散为真空都需要无限大能量. 即, 拓扑孤子不衰减的强健稳定性特征本质上源于场的基态简并. 与此类似, 对于Sine-Gordon方程, 其拓扑荷Q= 1/2π ·[φ(+∞) −φ(−∞)] =n, 其中n为整数, 且|n| > 1对应多孤子解, 亦称孤子晶格(soliton-lattice)解(Remoissenet 2013). 在图49所构建的超材料中, 考虑θ|x=0= 0以及周期性边界条件, 可得由λφ4方程(68)所描述的周期性拓扑孤子解为 根据图49 (f)可以发现, 拓扑孤子解式(70)和实验与有限元模拟结果一致性较好, 证实了有序局域变形样式中位于两相界面处的拓扑缺陷即为由λφ4方程所刻画的kink-antikink对. 该理论模型的拓扑激发, 源自于超材料系统中的元胞存在着两个极化相反的简并基态−内凹与外凸极化变形. 在该有限尺寸的孤子晶格中, 每一个kink之后都有一个antikink的紧随生成(图48 (d)(e)和图49 (c)). 类似的现象还广泛存在于其他非线性物理领域, 典型的如力学传输线、导电聚合物以及铁电体系统等(Dauxois et al. 2006, Remoissenet 2013). 需进一步指出的是, 静态拓扑孤子的非线性激发并不局限于特定样式的超材料结构, 而取决于元胞多稳态原位势与元胞间强耦合能的竞争中, 所主导的系统相变类型以及能量存储和释放的方式, 该理论机理具有广泛的适用性. 由此, 可进一步建立在超材料中激发静态孤子晶格、编程有序局域变形的统一性策略, 提出普适性物理框架: (1)基态转变型元胞. 设计超材料元胞以使得: 随外界激励持续增大并超出临界值(|ε| ≥|εc|)时, 元胞原位势Peff(θ)可经历由单基态向简并双(多)基态的转变. 以图50为例, 其力学量须满足这一刚度条件明确了超材料变形模式转变时, 可触发系统序参量θ分岔和结构相变的发生, 构成非线性拓扑激发的必要条件(图50 (a)(b)). 图50 (2)满足强耦合条件. 为了实现规则有序的非平凡激发, 相对于基态间势垒高度, 元胞间还应该满足强耦合作用条件. 其力学量须满足这一刚度条件确保了原位势基态转变以及序参量对称性破缺时, 超材料位移型相变的发生以及静态周期性拓扑孤子的激发(图50 (c)). 图50形象地刻画了这一普适性静态孤子框架的物理图像. 基于该理论框架, 设计“方块”、“杆系”与“圆−椭圆”多孔超材料, 在与图48相同的加载与边界条件下, 依次可激发出2, 3, 2对antikink/kink孤子(图50 (d)). 序参量空间分布的实验、模拟与理论结果明确证实了普适性框架的有效性和实用性(图50 (e)). 该物理框架限定了由力学量表征的能量关系, 而各刚度量又关联于元胞几何参数. 事实上, 通过适当几何设计, 在κ= 1类的超材料中, 还能实现宏观均匀的平凡激发以及其他类型的非平凡激发: ①约束(1)不成立, 抑或约束(1)成立但存在额外约束θ=const.. “球链”将始终全部稳定于系统唯一的基态, 抑或多基态之一. 此时, 超材料发生宏观均匀变形, 系统拓扑荷Q= 0. ②约束(1)成立, 但约束(2)不成立. 则元胞间弱耦合(耦合能远小于等效原位势能垒). 在此情形下, 弱连接的非线性“球链”随机的分布于基态之间. 与此对应, 超材料将会发生有序−无序(order-disorder)相变(Chaikin et al. 1995), 表现为随机的局域化样式, 系统拓扑荷Q≠ 0且依赖于边界条件. 由该物理框架所支配的拓扑孤子晶格激发, 在力学超材料中不仅展现出了“反常”的特征尺度与尺度效应, 更是突破了长期以来人们认为局域变形通常是缺陷敏感且其尺寸和位置随机性强而难以预测的传统认知. 事实上, 不仅在宏观力学体系, 此类鲁棒的非平凡激发还广泛存在于众多跨尺度的多基态系统之中, 如受限空间中的粒子输运(Sisan et al. 2014), DNA 碱基的旋转(Peyrard et al. 1989), 铁电畴变(Frazier et al. 2017)和长约瑟夫森结的磁通量子传输(Frazier et al.2017)等−看似“毫不关联”的、跨学科领域的自然现象背后, 均可由相同的数学物理本质所支配. 构建联系此类现象背后的更一般的数学物理框架, 将会为在更宽广的物理境遇中探索高维系统的非线性拓扑激发、可控的几何相变, 以及揭示更复杂局域化现象的机理本质铺垫崭新的道路. 桁架结构根据其稳定与否可以分为超静定结构、静定结构和机构. 根据结构中包含的节点和连杆数目能够粗略估算能否构成稳定桁架, Maxwell (1864)最早给出了构成静定桁架结构的必要条件. 近期研究表明, 对于特定桁架结构, 其机构模式和自应力模式只能以向体内衰减的边界态形式存在, 同时也具有与前述波动现象类似的体−边对应关系, 即边界零能模式(zero mode)受到无限大体的能带拓扑性质的保护. Kane等(2014)发现满足Maxwell临界条件的桁架具有内禀指向性, 由一拓扑极化矢量表征. 与电极化材料中正负电荷向材料的两边聚集类似, 非平凡拓扑极化的Maxwell桁架结构, 零能模式与自应力模式也根据界面与拓扑极化的相对方向向材料两侧聚集. 零能边界态的分布由体态拓扑性质决定, 对边界局部杆件长度、刚度和节点质量等扰动不敏感. 该工作开启了准静态结构力学性质拓扑方向性的研究, 例如, 基于拓扑保护的自应力状态实现点阵材料局部可控屈曲变形(Paulose et al. 2015a), 将拓扑极化向量与Burgers矢量相结合构造了点构型松散模式(Paulose et al. 2015b), 设计外硬内软的防护器件等(Mao et al. 2018). 本小节对这一新方向做简要介绍. 考虑nb根杆和ns个节点构成的d维自由桁架, 构成稳定结构所需最少杆数目由Maxwell准则nb=dns−f(d)给出, 其中f(d) =d(d+1)/2为刚体运动数. 一个桁架存在的零能模式数由N0=dns-nb=M+f(d) 给出, 除f(d)个刚体模式外, 另有M个机构模式, 在物理学领域也称松散模式(floppy mode). 一般将刚好满足该准则且处于临界稳定状态(M= 0)的桁架称为Maxwell结构,或等静定结构(isostatic structure), 例如图51 (a). 但Maxwell准则并非适用所有情形, 对于图51 (b)的结构, 其nb,ns与图51 (a)相同, 却显然有M= 1. Calladine (1978)指标定理对Maxwell准则进行了修正 其中NSS为结构包含的自应力(self-stress state, 无需外部节点力即能自平衡的杆内力)状态数.图51 (b)中结构中左侧超静定, 含自应力状态NSS=1, 因此, 式(71)给出作为整体N0= 4,M= 1.对于无限大周期点阵桁架, 引入配位数(每个节点所连杆数)Z≡ 2nb/ns, 根据Maxwell条件临界配位数满足Z=ZC= 2d− 2f(d)/ns≈ 2d, 以二维结构为例, 平均配位数Z= 4, 如图52 (a)和52(c)中所示的Kagome点阵(规则型与扭曲型)是当前研究最广泛和最深入的Maxwell周期点阵材料.周期无限大Maxwell结构节点与连杆数目满足nb=dns, 因而恒有N0=NSS, 其分析通常采用单个胞元结合周期边界进行. 周期边界去除了刚体旋转模式, 有f(d) =d, 但也同时限制了胞元产生整体宏观应变, 使结构的动定、静定条件界定比有限结构相对复杂(Guest et al. 2003). 对于无限大周期桁架结构, 若满足Maxwell条件M= 0, 必有N0=NSS=d. 图51 图52 定性分析从周期无限大Maxwell桁架中截断相应杆件, 形成Nx×Ny个胞元构成的有限结构.设有限结构包含节点数ns, 则需截断杆件数为量级. 根据式(71), 由于nb减少,N0−NSS将由0增至与减少杆件相同量级; 同时, 结构截断通常伴随自应力状态NSS的消失, 指标定理要求截取的有限结构包含量级的零能模式. 但是, Calladine指标定理无法给出这些零能模式为体态还是边界态以及分布情况. 桁架结构分析通常采用矩阵方法, 结合奇异值分解能够清晰给出其机构和自应力模式, 并直接导出Calladine指标定理(Pellegrino 1993), 该方法也适用于分析周期无限结构(Hutchinson et al.2006). 结构几何协调关系由Bu=e描述,e和u分别为杆伸长和节点位移向量,B为nb×dns协调矩阵; 桁架平衡关系由At= −f给出,f和t分别为外部节点力和杆件内力向量, 且由虚功原理容易得到B与A互为转置. 自应力状态与零能模式分别位于平衡矩阵A和协调矩阵B的零空间. 取杆刚度和节点质量均为单位值,D=AAT构成结构的对称刚度矩阵, 系统动力学方程为Du=f. 对于周期桁架中的布洛赫波, 上述协调方程、平衡方程及动力学方程进行Fourier变换得到 此时,t(q),e(q),u(q),f(q)均为胞元内节点和杆相关的复振幅,A(q)与B(q)互为厄米共轭,q为布洛赫波矢,ω为角频率. 值得注意对于Maxwell周期桁架, 矩阵A和B为方阵. Calladine指标定理在波矢空间仍然成立. 对图52 (a)所示的规则Kagome结构利用方程(72)进行布洛赫波分析, 单胞节点和杆数分别为3和6. 由于规则Kagome桁架存在贯穿结构的直线杆系, 在周期条件下每条贯穿直线杆系能够支撑自应力状态. 贯穿杆系沿3个不同方向, 与相应布里渊区中的ΓM线垂直(图52 (b)), 因此对于这些线上每个波矢q, 均存在自应力状态. 根据Calladine指标定理, 对这些波矢也必存在相同数量的零能模式.图52 (a)中也分别以蓝色块和红色直线给出了零能模态与自应力模式的示例, 这两个模式为波阵面水平的脉冲形式, 可视为垂直ΓM线上一系列零模态(红色点)的叠加.图52 (b)的绿色线事实上给出了第一支色散曲面ω= 0的等频线, 可见与多数稳定结构不同,规则Kagome桁架色散曲面零频率点不仅仅位于Γ点. 若截取图52 (a)所示的有限结构并去除周期边界, 贯穿直线杆系的自应力被释放, 数量上等同于杆−节点数目相比于周期Maxwell条件的失配, 因此, 规则Kagome桁架中不会增加零能模式, 且零能模式仍为图52 (a)所示的体态. 对图52 (c)所示的扭曲Kagome桁架进行相同分析, 将得到迥异的结果. 尽管节点与杆件连接关系与前者相同, 但由于结构中贯穿直线杆系变为曲折, 在有限q下不能存在自应力状态. 在Γ点处N0=NSS= 2, 对应于刚体平移, 除此之外N0=NSS= 0. 因此扭曲Kagome桁架在ω= 0时在除Γ点外打开简并. 同样考虑截取图52 (c)所示的有限自由结构, 由于不存在原有自应力状态补偿杆-节点失配, 因此有限结构中必然出现新的零能模式; 又由于扭曲Kagome桁架缺乏零能体态,这些零能模式只能存在于结构边界, 并向体内衰减. 前述分析可见: (1)尽管连接关系相同, 规则与扭曲Kagome桁架具有显著不同的声子行为, Calladine指标定理无法体现; (2)有限Maxwell桁架零能模式的分布与无限大体的能带结构具有密切关系. Maxwell桁架具有内禀指向性, 由一拓扑极化向量表征 其中ai为晶格矢量,ni为复平衡矩阵A(q)行列式相位的缠绕数, 定义为 其中φ为detA(q)的相位角,Ci为连接布里渊区两点[q,q+bi]的闭合积分路径,bi为倒格基矢量.界面/边界零能模式和自应力模式分布受拓扑极化影响, 同时在整体上也必须服从Calladine指标定理, 因此, 综合这两种因素给出边界/界面态零能模式的指标定理. 考虑Bravis格点阵材料界面或边界, 其法向可由一倒格矢量G标定, 设界面上每个单胞的零能模式和自应力模式数为界面指标定理由下式给出 图52 (c)所示的扭曲Kagome桁架是拓扑平凡的(RT= 0), 为产生拓扑极化需要对Kagome结构进行更一般的变形, 如图52 (e)所示. 扭曲过程仍然保证Kagome点阵的Bravis格不变, 利于保证不同拓扑相的Kagome桁架能够顺利连接以构成界面. 由于可固定三个单胞独立节点中的一个不变, Kagome桁架的一般变形由四个参量决定. 采用文献(Kane et al. 2014)的参数化, 给定三个晶格矢量(a1,a2,a3= -a1-a2), 单胞节点位置由四个独立参数(x1,x2,x3;z)确定:d1=a1/2 +s2,d2=a2/2 -s1,d3=a3/2, 其中s1=x1(a3-a2) + (z/3 +x3-x2)a1,s2=x2(a1-a3) +(z/3 +x1-x3)a2. 参照图52 (e)参数的几何意义, 参数xi描述变形桁架相对于规则Kagome桁架中贯穿杆系的曲折程度,z给定两个相邻三角形尺寸. (0, 0, 0; 0)与(x,x,x; 0)分别对应规则与扭曲Kagome桁架.图52 (f)给出Kagome桁架在z= 0和x1+x2+x3= const.约束下连续变形的相图, 结构在xi变号时产生拓扑相变从而具有内禀指向性, 具有拓扑极化向量 图53 (a)所示为不同拓扑相的Kagome桁架所构成的界面系统, 其中两侧区域为拓扑平凡的扭曲Kagome桁架(参量(0.1, 0.1, 0.1; 0)), 中间部分为参量(0.1, 0.1, −0.1; 0)的变形桁架, 拓扑极化向量如图所示. 对该结构施加周期边界, 由于没有截断杆件, 因此不产生局部指标失配而在左右两个界面处分别有由于两个界面处ν˜T反号, 对于结构整体而言满足全局Calladine指标约束N0−NSS= 0, 但拓扑极化导致零能机构模式集中于左侧界面, 而自应力模式集中于右侧界面.图53 (b)给出了超胞结构随qx(与界面平行)变化的色散关系, 其中负频率曲线由刚度矩阵D=AAT的超对称伴随矩阵ATA得到. 图中两个零频率分支分别对应两个界面上的机构模式和自应力模式. 与波动行为中的拓扑现象类似, 在变形Kagome桁架打开除布里渊区原点处的零频率简并, 并且体态具有非平凡拓扑相时, 该零能模式受到拓扑保护.图53 (a)中也给出了对应qx= π的机构与自应力边界态, 分别以箭头和色线表示. 图53 Maxwell桁架系统处于临界稳定状态, 其零能模式的研究对于理解材料的物态转换、刚度与强度的本质、散体流动机制具有重要意义, 长期为材料物理学界关注. 拓扑极化性质无法由局部连接关系和几何构型直接呈现, 证明这一简单系统可蕴含极丰富的物理机制. 当前, 拓扑零能模式的研究还局限于严格的Maxwell桁架系统, 在分析上基于矩阵哈密顿算符. 对于不满足Maxwell条件的弱超静定桁架(非方阵算符)甚至连续体复合材料(微分算符), 是否存在类似的拓扑“软”模式是值得探索的问题. 此外, 拓扑方向性作为材料一种新的内禀属性, 在传统连续介质力学和本构关系框架中无法得到体现, 寻求高阶连续化理论以表征这一性质也正在引起关注(Mao et al. 2018, Sun 2020). 由于周期结构的低频模式决定材料宏观力学响应, 拓扑零能模式的丰富性、鲁棒性和可操控性无疑为传统点阵材料设计带来新的契机. 本文系统介绍了近年来弹性波拓扑绝缘体相关研究进展. 论文在引言部分对拓扑绝缘体在电子波研究中的起源做了回顾. 随后, 以离散质量弹簧模型为例对拓扑绝缘体研究有关概念、设计与分析方法等做了详细阐述. 第3 ~ 第5小节分别介绍了谷霍尔、霍尔及自旋霍尔绝缘体设计原理、波动规律及取得的研究进展. 第6小节以二维角落态为例简单介绍了高阶拓扑绝缘体. 目前来看, 针对二维弹性波的拓扑绝缘体研究比较完善, 常见拓扑绝缘体都已实现并得到验证, 后续研究主要可以从以下方面进一步拓展: (1)三维弹性波拓扑绝缘体研究. 三维材料有更丰富的带结构特征, 例如, 能带可在三维动量空间某一位置形成线性简并, 该简并点称为外尔点(Weyl point), 简并点可以相互连接构成封闭的拓扑节线(nodal line), 拓扑节线可进一步相互嵌套成节线链(nodal chain), 这些所谓拓扑半金属(topological semimetal)材料均存在独特表面态. 相关研究在声波、电磁波系统中研究较多, 也逐渐被拓展到弹性波领域(Ganti et al. 2020). 三维拓扑绝缘体的高阶拓扑特性也有更多可能, 如在零维角点的拓扑角落态与一维边界的铰链态. (2)非厄米特(non-Hermitian)系统的拓扑现象也是近来热门研究(Leykam et al. 2017, Shen et al. 2018, Zhang et al. 2019, Gao et al. 2020). 实现非厄米特性一般需要系统包含损耗或者增益效果, 这导致系统的能量不再守恒, 系统的特征频率从实数变为复数. 这类系统也可以通过拓扑不变量刻画, 系统边界也允许常规拓扑绝缘体中的拓扑保护态, 但其拓扑相变不是通过能带简并而实现, 而是通过奇异点(exceptional point)进行转变. 在弹性和机械系统中, 这类新奇拓扑现象的研究比较少. (3)弹性波拓扑绝缘体的应用探索. 后续研究除了揭示弹性波拓扑绝缘体机理外, 更应该注重拓扑界面态与实际波动控制应用的结合, 这是目前拓扑绝缘体研究比较欠缺的. 利用弹性波拓扑边界态具有的免疫缺陷、背散射抑制等特性, 一方面, 可设计能量传输效率更高的无损检测、声波传感器拓扑器件; 另一方面, 可降低器件对结构加工精度等的要求, 更利于实际应用. (4)拓扑现象的连续化描述. 目前拓扑现象多数是通过具体微结构来呈现和讨论的, 这制约了新拓扑材料的设计, 如果能在连续介质框架下建立描述拓扑现象的相关理论, 或将促进拓扑材料的设计与开发. (5)静态拓扑现象的进一步发掘研究. 除了第7小节的拓扑孤立子、Maxwell点阵中的拓扑零能模式外, 其他静力学现象中的拓扑或可进一步发掘, 如固体中的位错就对应着拓扑缺陷, 或可借鉴设计相关的静力学超材料. 致 谢感谢赵玉臣提供连续介质边界态相关素材. 国家自然科学基金(11632003, 1173207,11872111, 11972080, 11972083, 11991030, 12002030, 12072108)资助项目.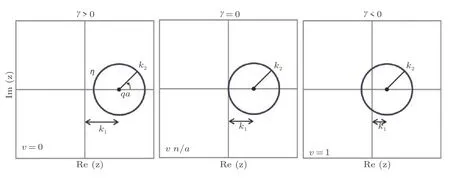

2.2 二维蜂窝质量弹簧系统









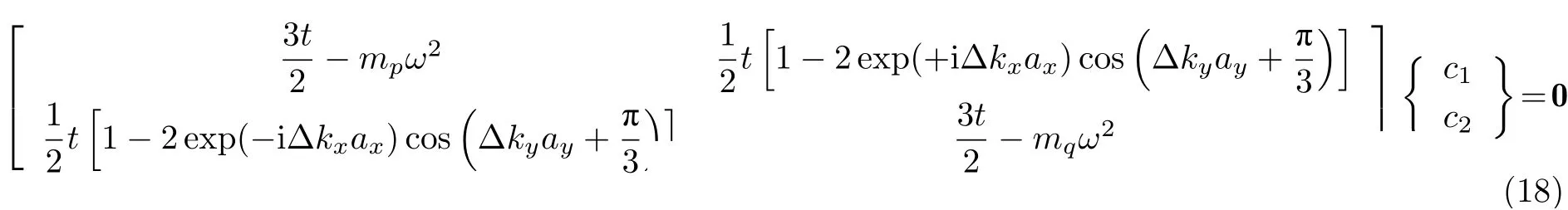

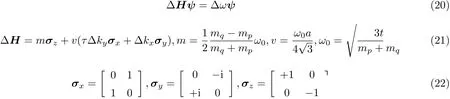

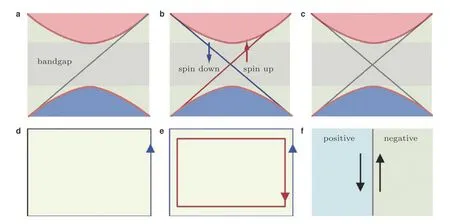
2.3 二维弹性波拓扑绝缘体分类
3 谷霍尔绝缘体研究进展
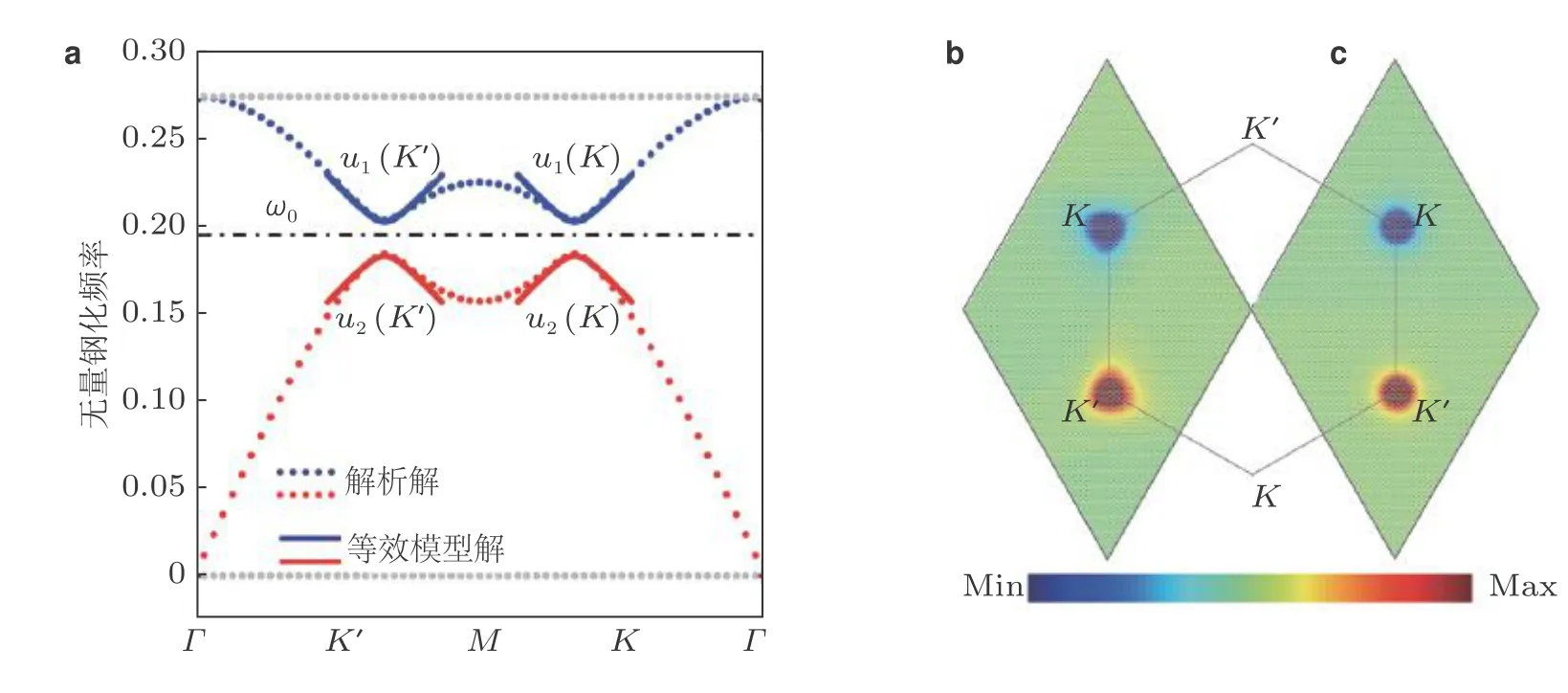
3.1 谷霍尔绝缘体设计



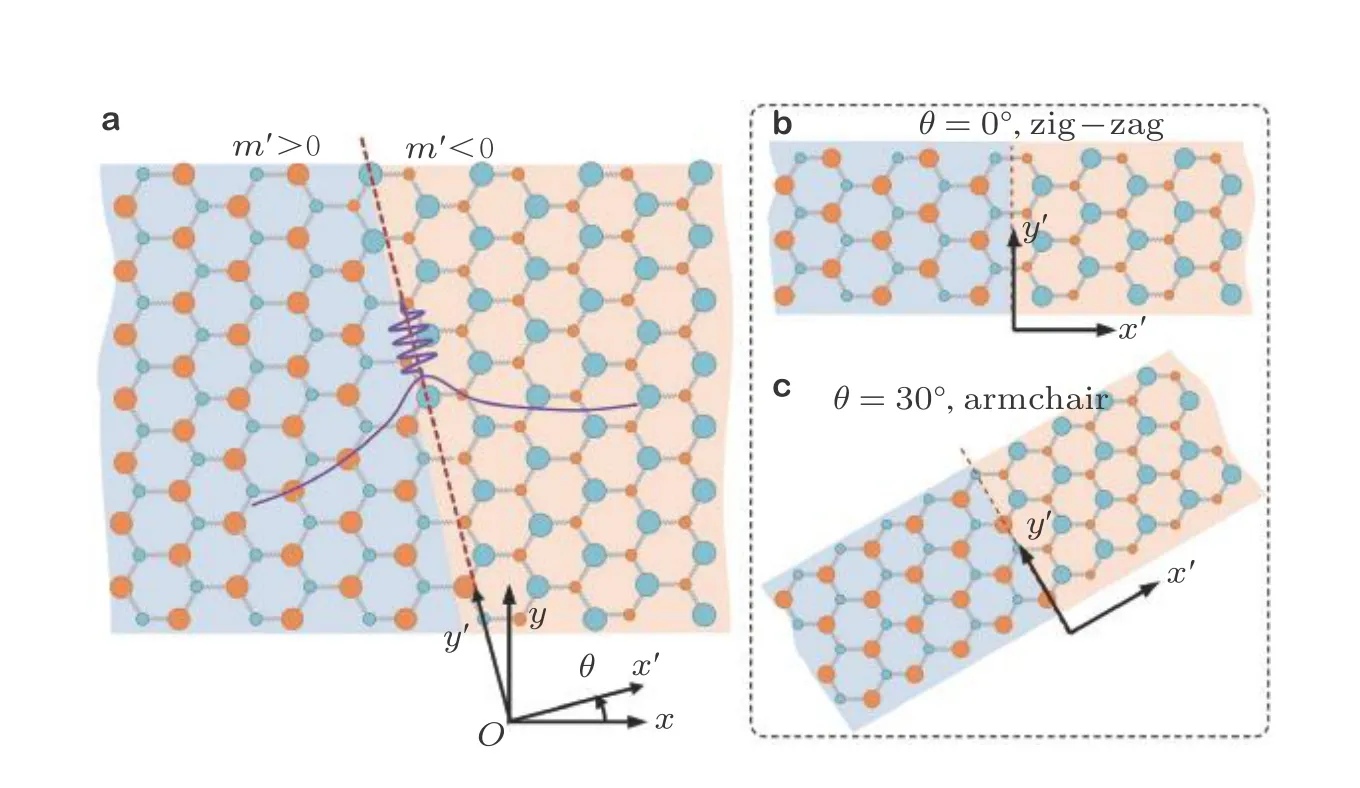
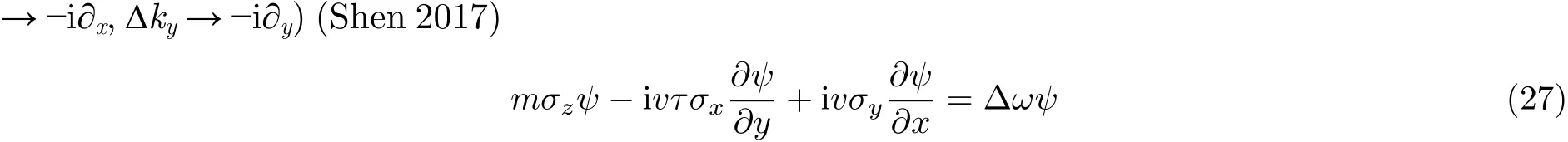
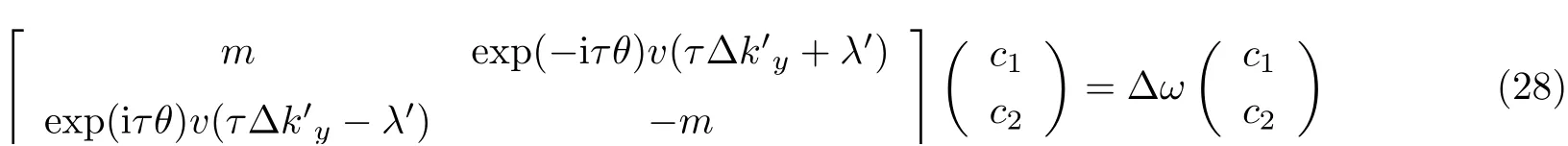


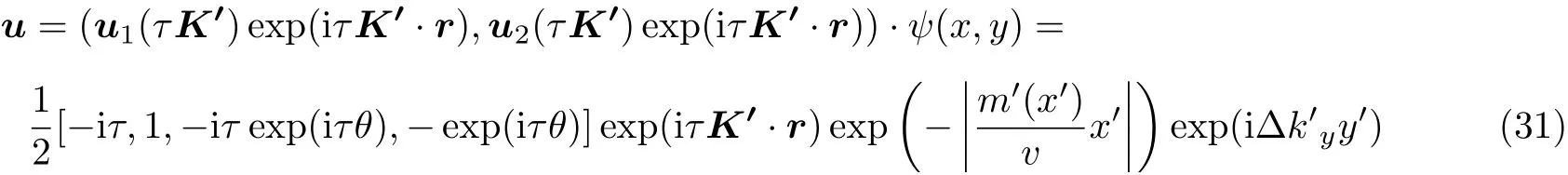
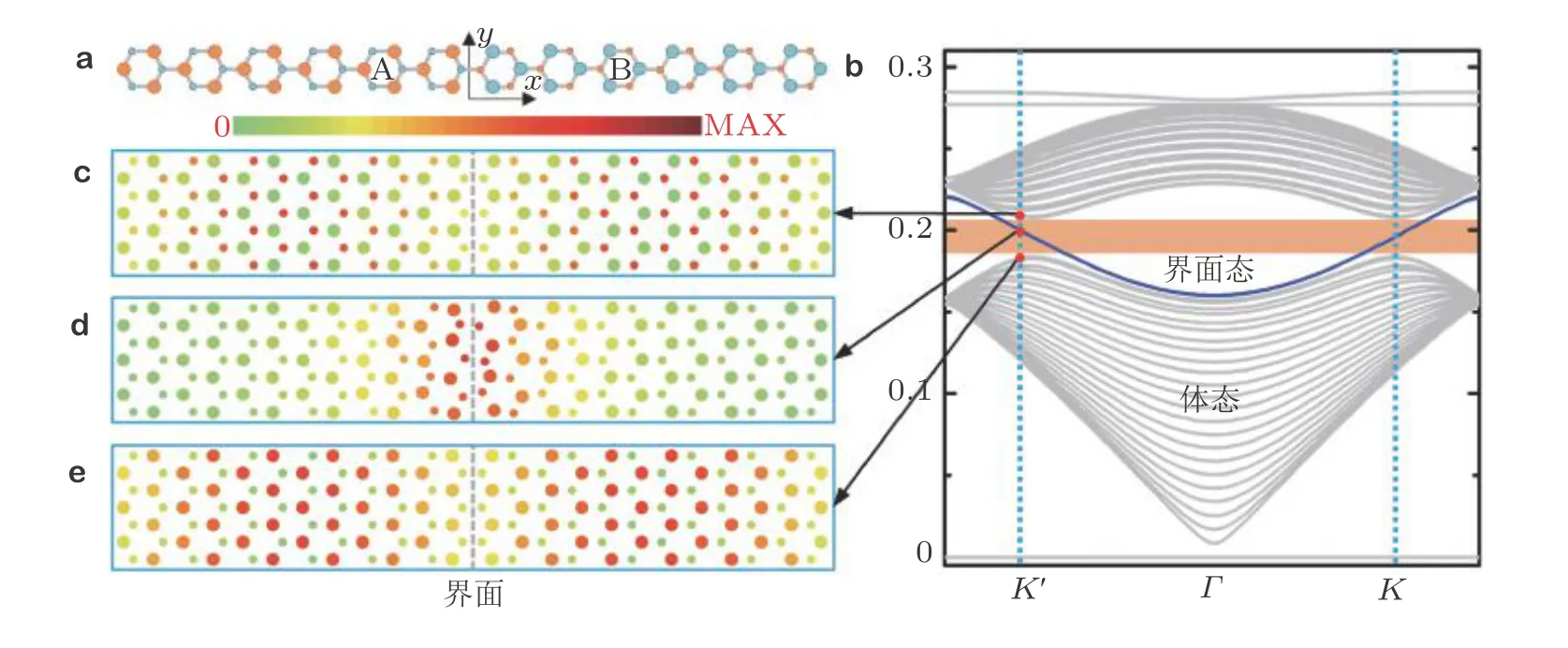

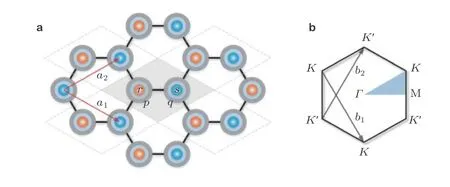


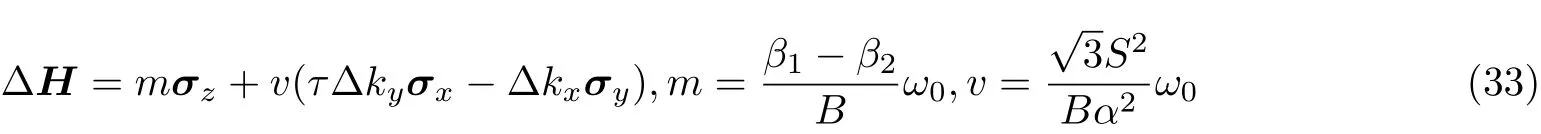


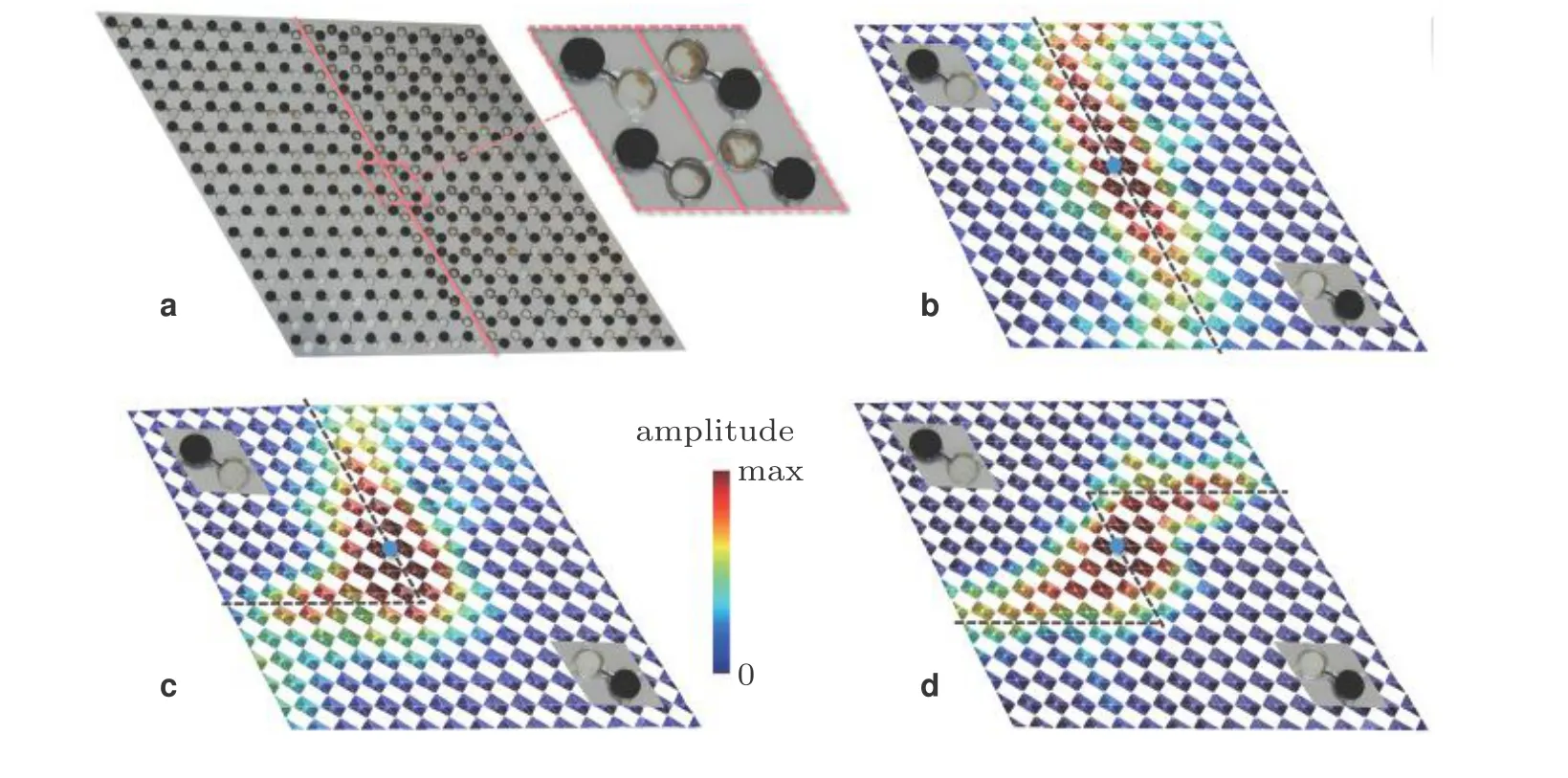
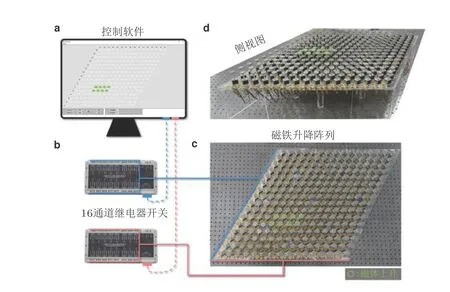
3.2 谷霍尔绝缘体实验

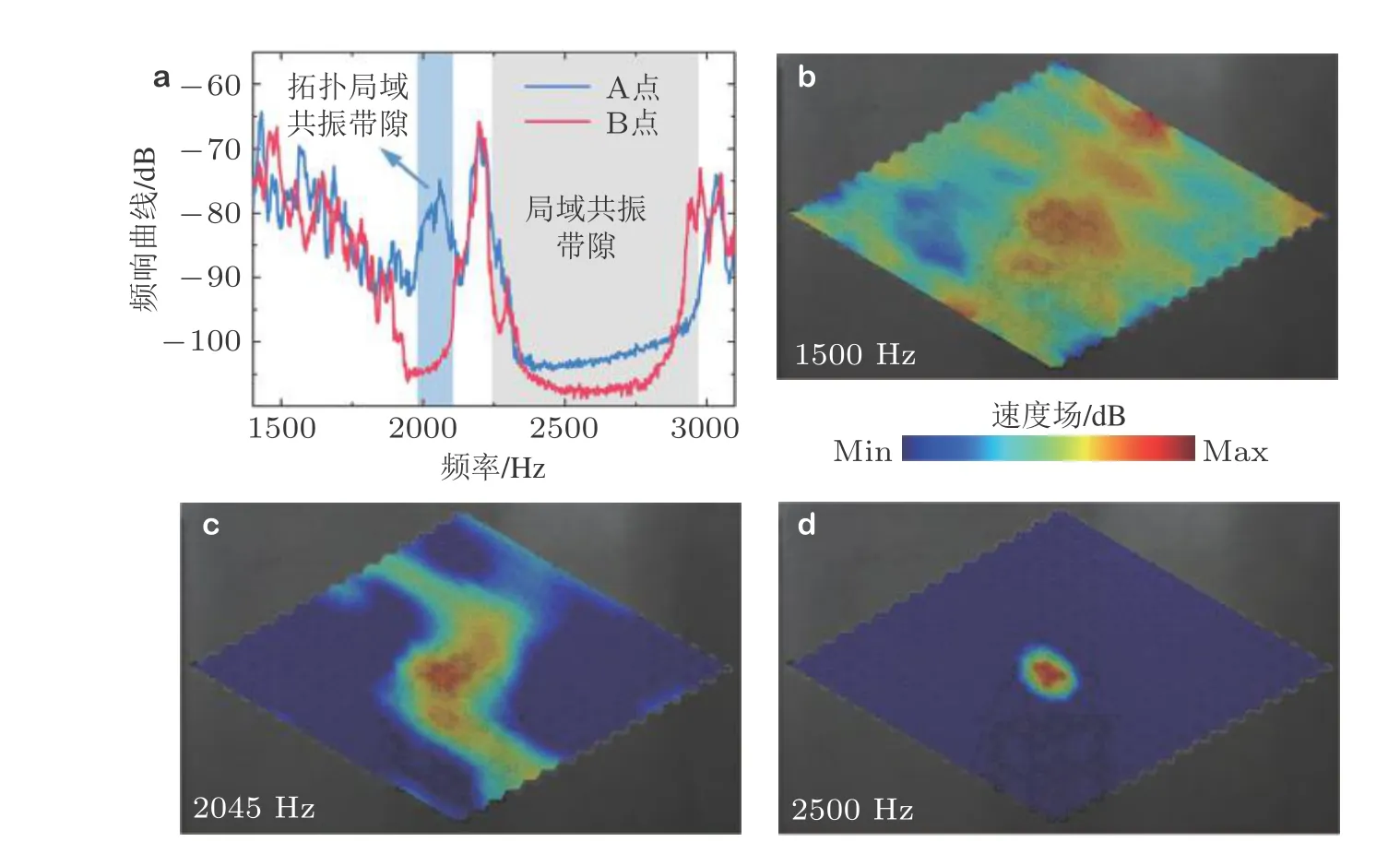



4 陈绝缘体研究进展
4.1 陈绝缘体设计
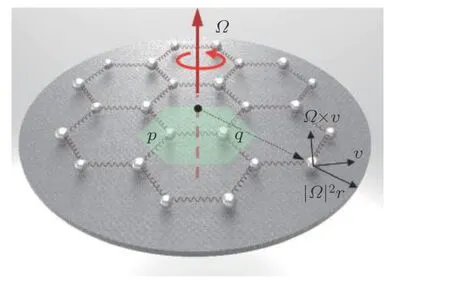
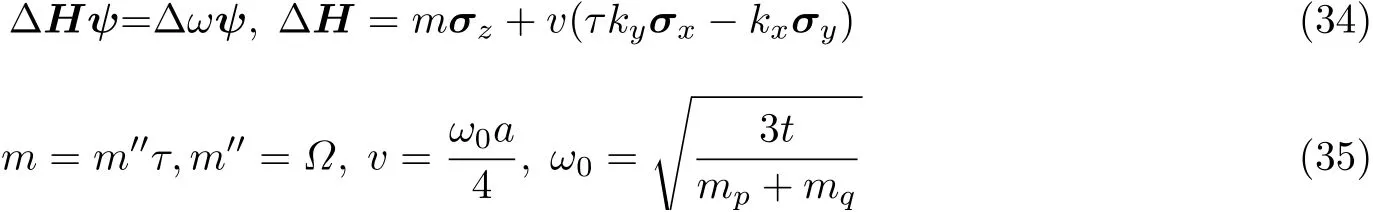


4.2 连续介质边界态

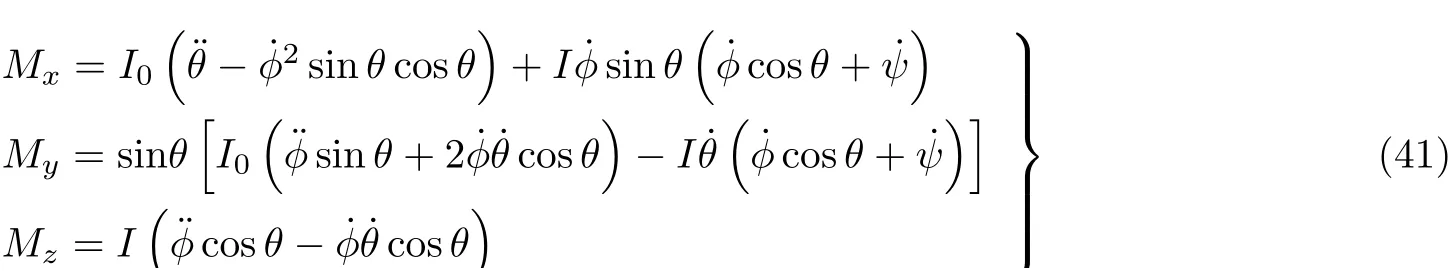







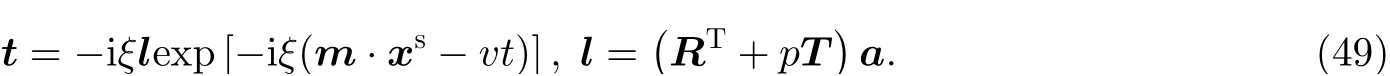

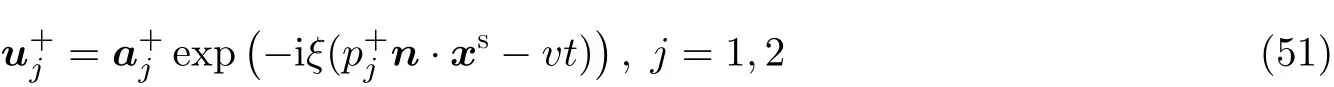

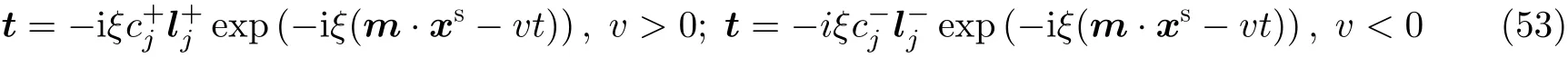

5 自旋霍尔绝缘体研究进展
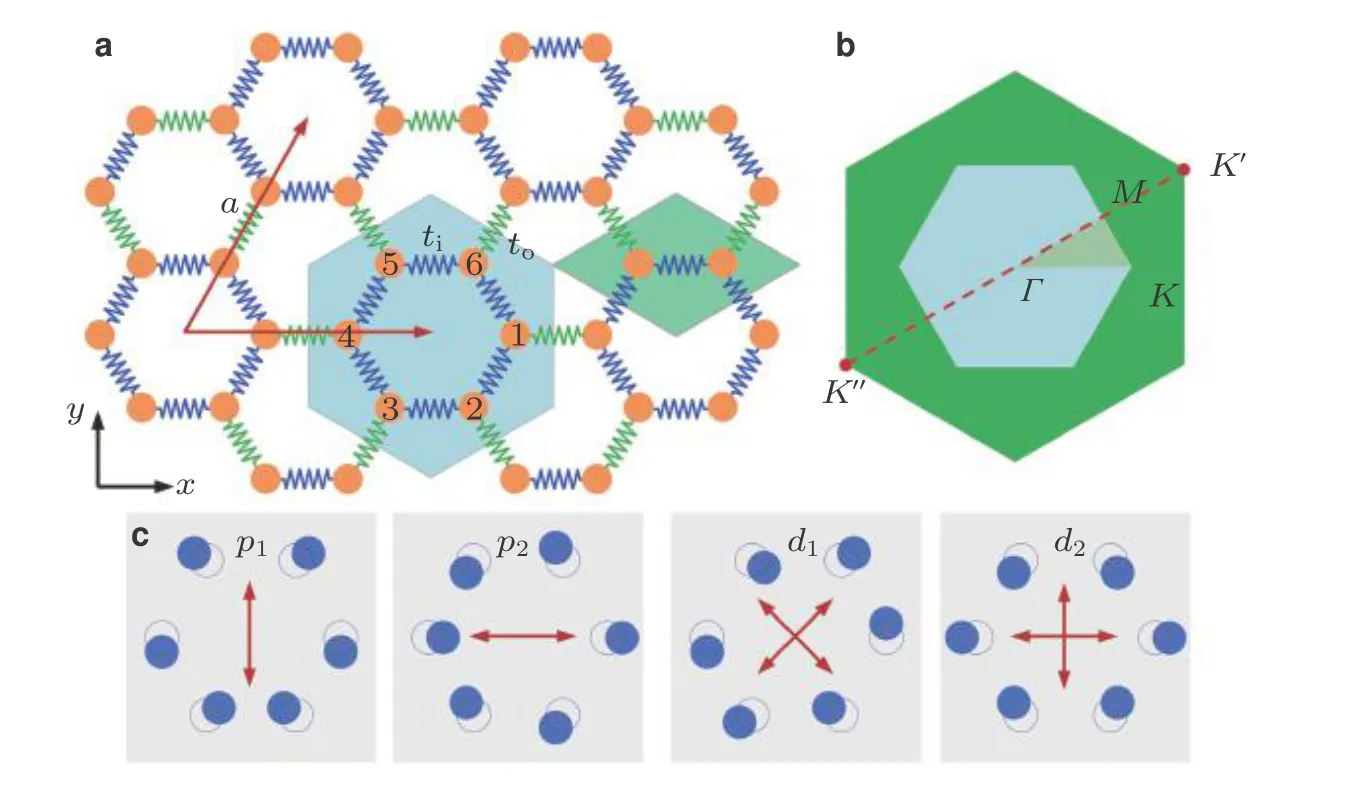
5.1 自旋霍尔绝缘体设计
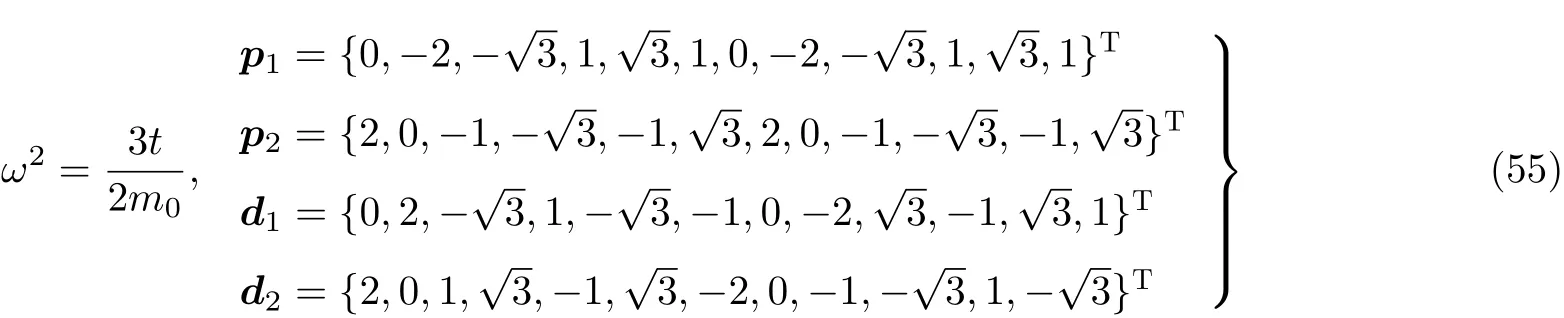
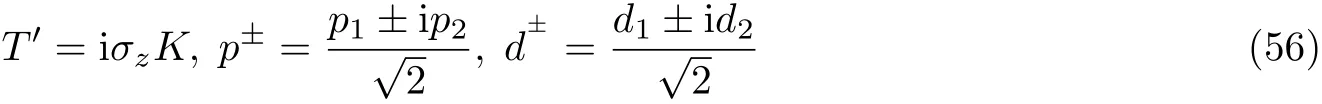

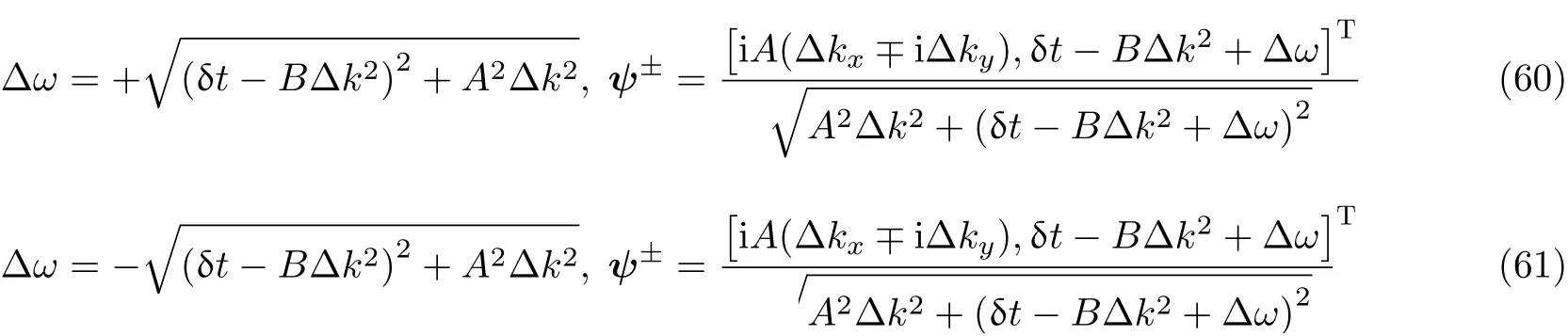
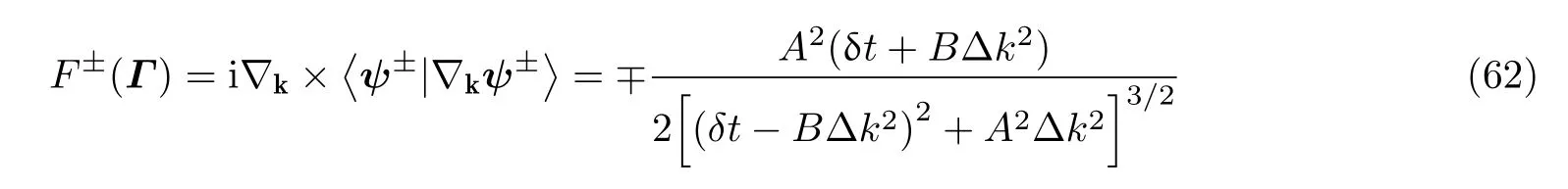
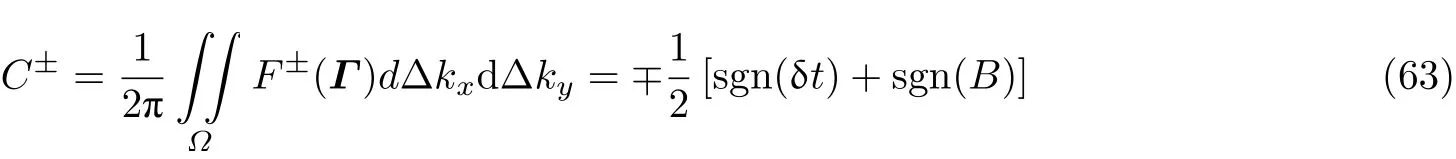





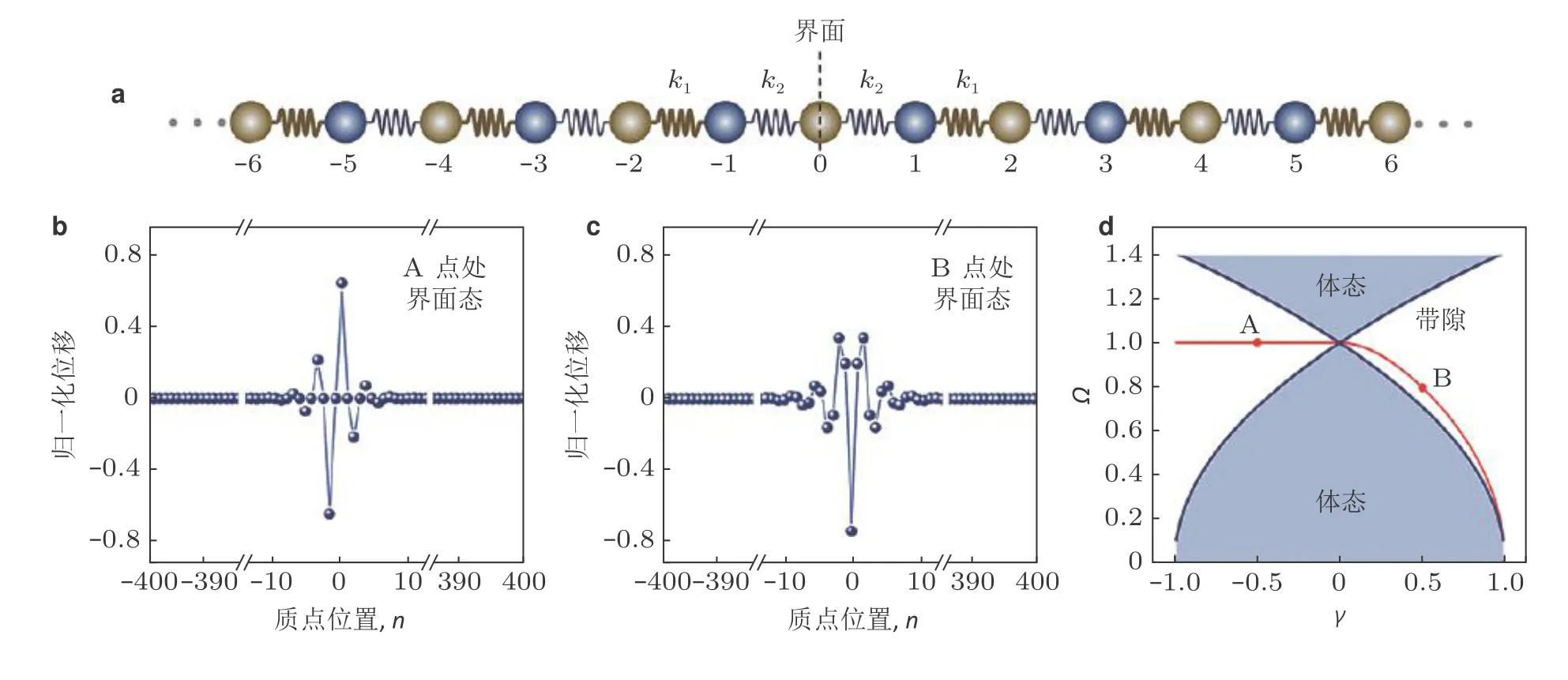
5.2 自旋霍尔绝缘体实验

6 高阶拓扑绝缘体与角态
6.1 高阶弹性声子晶体板的复合元胞分析
6.2 正六边形弹性声子晶体板的高阶角态分析与测试

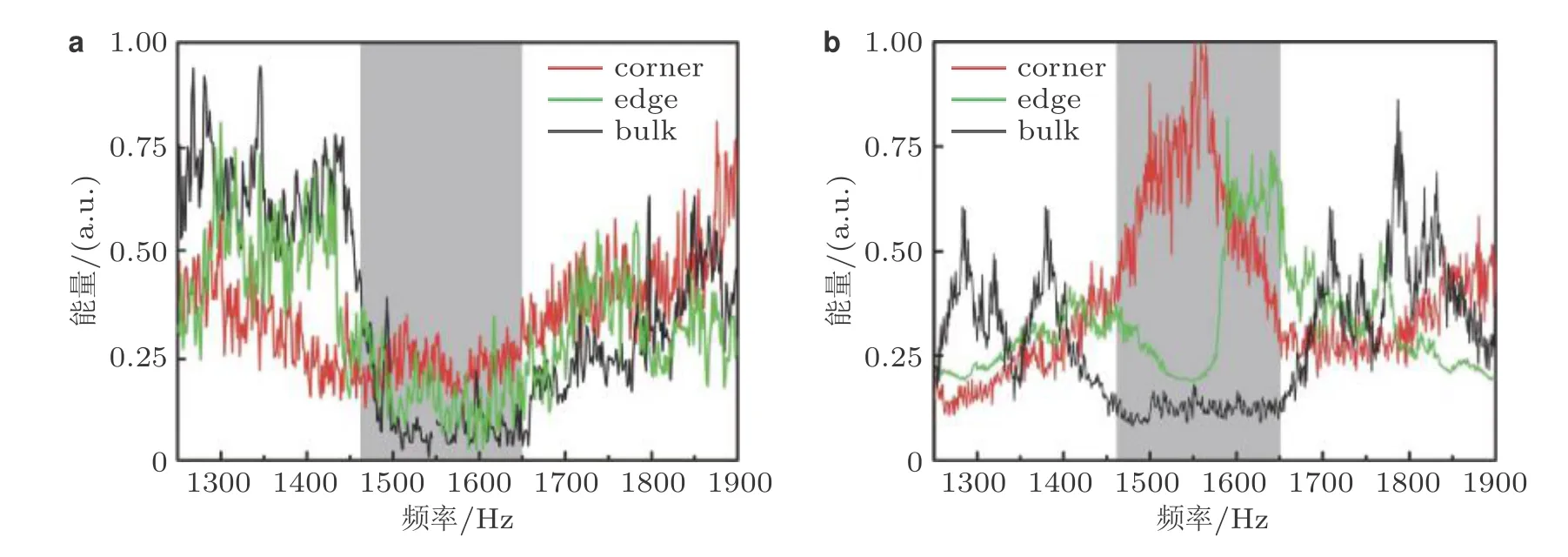
6.3 正三角形弹性声子晶体板的高阶角态分析与测试
6.4 高阶弹性声子晶体板的拓扑指数分析

7 静力学拓扑
7.1 拓扑孤立子







7.2 拓扑零能模式
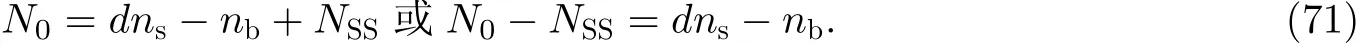
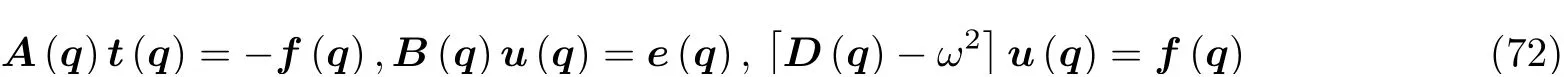




8 总结与展望
